油藏流固耦合分析的一种有限元-有限体积混合方法

吴大卫，邸 元，孙建芳

(1.北京大学 工学院，北京 100871；2.中国石油化工股份有限公司石油勘探开发研究院，北京 100083)

在油气开采过程中，孔隙流体压力的变化会引起岩石骨架应力的变化，从而导致油藏物性参数的改变，而这些改变又反过来影响孔隙流体的流动和压力分布[1-5]。对裂缝性油藏或低渗油藏等对应力较为敏感的油藏而言，这一效应更为明显[6-11]，因此需要考虑流固耦合进行计算。Terzaghi[12]引入有效应力的概念来研究流固耦合问题，提出了土的一维固结模型。Biot[13-14]建立了三维固结理论，并将其理论推广到了各向异性的多孔介质。Geertsma[15]与Verruijt[16]对Biot理论进行了推广，进一步发展了多相渗流与孔隙介质耦合作用的理论模型。Savage等[17]将Biot理论应用于横观各向同性的孔隙介质中。Zienkiewicz等[18]考虑了固相材料非线性的问题，在Biot的三维固结方程基础上提出了广义Biot公式。

针对流固耦合问题的数值模拟研究大多采用有限元方法。然而采用有限元方法离散时，位移和孔隙压力不宜采用相同的插值函数，从而导致编程实现较为复杂。Akai等[19]提出了一种有限元-有限差分混合方法来求解饱和多孔介质的Biot方程。Oka等[20]则将这一方法应用到了饱和土液化的数值分析。在此基础上，本研究建立了一种流固耦合分析的有限元-有限体积混合方法。这一方法对平衡方程与渗流方程分别采用不同的数值离散方法，并可以对两个方程使用不同密度的计算网格。通过对一维固结问题和二维单井定压生产问题的数值模拟，验证了本文方法的有效性。

1 数学模型的建立

1.1 力学平衡方程

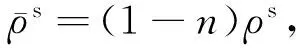
对固相和液相分别建立力的平衡方程：

(1)

(2)

引入Zienkiewicz的u-p假定，即认为液相对于固相的加速度很小，代入各相的平衡方程中,并引入各相应力与孔隙压力的关系，可得：

(3)

式(3)即为流固耦合问题中考虑了固相位移的达西定律表达式，可见在考虑了固相位移后达西定律中出现了固相位移的相关项，这也导致了离散后的平衡方程和连续性方程中会出现耦合项。

将固相与液相的平衡方程相加，可以得到总体的平衡方程：

(4)

1.2 连续性方程

根据雷诺输运定理，可以得到固相和液相的质量守恒方程，分别有：

(5)

(6)

将两方程相加，并进行化简后可以得到：

(7)

代入考虑固体骨架位移后的达西定律表达式式(3)，假定固体介质不可压缩，并引入液相的压缩系数C，整理后可得渗流连续性方程：

(8)

2 离散方程的建立

分别对上述平衡方程和连续性方程采用有限元法和有限体积法进行离散。

对力学平衡方程进行有限元法离散，可以得到在空间域内离散后的平衡方程：

(9)

式(9)中：[M]为质量矩阵;{un}为节点位移;[K]为刚度矩阵;{KV}为体刚度向量;{Fd}为荷载相对增量;{Rd}|t为有效应力相对增量。

对式(9)在时间域内采用Newmarkβ方法离散，从而可得到有限元法离散后的力平衡方程。

对上述流固耦合问题的连续性方程采用有限体积法进行离散。在单元内对连续性方程取积分弱形式，并引入高斯定理，可得：

(10)

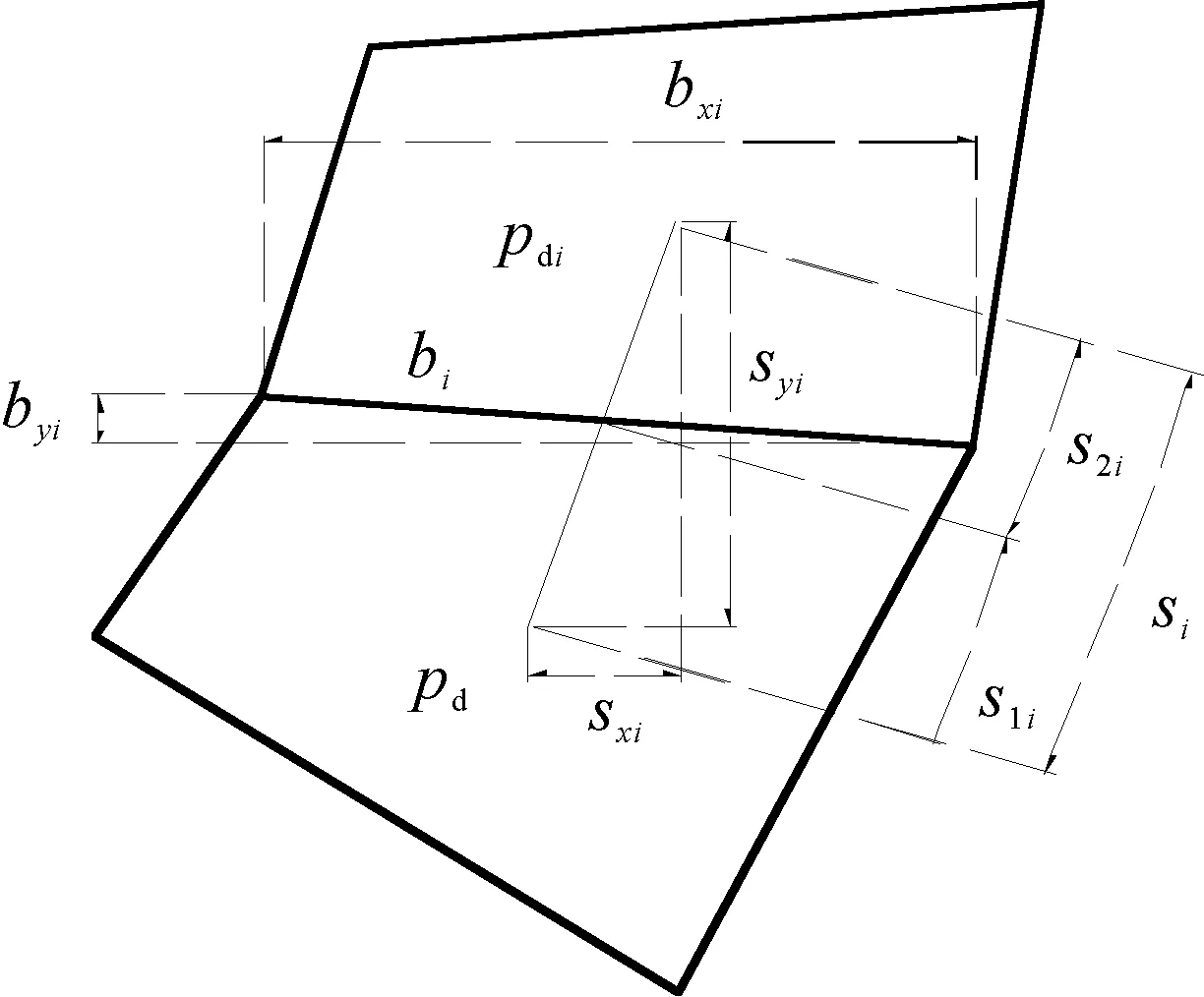
图1 有限体积法中相邻的2个单元Fig.1 Two adjacent elements in FVM

式(10)中：pd为孔隙压力相对初始状态的增量；ni为垂直于边界的方向向量；V为积分区域体积；S为积分区域表面积。

对式(10)等号左侧的第一项仍采用有限元法离散，对最后一项采用有限体积法离散，对于图1的平面四边形网格情形，该项可写为：

(11)

式(11)中：vx i、vy i分别为2个方向的流入速度；nx i、ny i分别为方向向量的分量；bi为单元的第i条边。

采用Newmarkβ方法在时间域离散，并对变量进行简化：

(12)

(13)

(14)

(15)

式(12)～(15)中：t为时间坐标，Δt为时间步长。

离散后可得连续性方程为：

(16)

式(16)中：t与t+Δt代表变量的时间步取值。

3 储层区域采用精细网格

流固耦合问题的数值分析中，力的平衡方程与渗流方程的计算区域往往是不同的，渗流方程的计算区域对平衡方程的计算区域而言只是其一个子区域[21]。以油藏数值模拟为例，真正需要进行渗流方程求解的只有储油层的区域；而力平衡方程的计算应当在包含整个储层的更大区域内进行，这样才能保证对应力状态进行正确的求解。

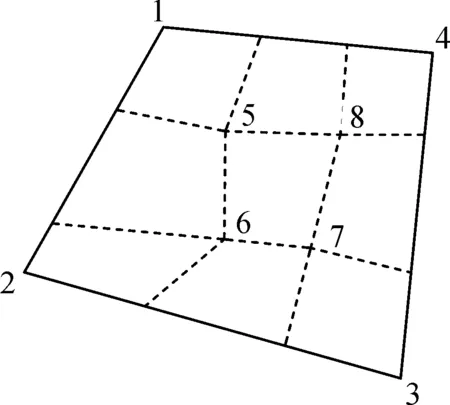
图2 有限元法的网格和有限体积法的单元Fig.2 Grids in FEM and elements in FVM

有限元-有限体积混合方法对采用有限元法求解力平衡方程的区域和有限体积法求解渗流方程的区域，使用不同精细程度的网格单元。具体实现方法为：在整个计算区域进行有限元的网格划分；而在渗流场涉及的储层区域，将有限元的网格进一步细分，即将每个有限元中的单元离散为多个更小的单元作为有限体积法中使用的单元。

下面以储层区域平面四边形网格为例进行说明。如图2所示，实线表示有限元法中所使用的网格，而虚线表示的是有限体积法中使用的细分的子单元。图2中节点5～8围成的子单元，其节点位移向量可以通过其所在有限元单元的节点位移插值函数得到：

{u}={u5,u6,u7,u8}T=[N′]{un}。

(17)

式(13)中：{u}为子单元位移向量；{un}为单元节点位移向量；[N′]为插值函数组成的转换矩阵。

于是，可以分别得到有限元单元的平衡方程与子单元的连续性方程如下：

(18)

(19)

式(18)中：pavg为单元的平均孔隙压力。可见，对于每个有限元单元，方程由1个力平衡方程和9个连续性方程组成，对拼装后的总体方程组求解，就可得到整个问题的计算结果。

流固耦合问题的计算中，需要考虑应力或应变对固体介质孔隙度和渗透率的影响。本文采用如下的经验公式[22]表示孔隙度及渗透率与应力的关系：

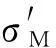
(20)

(21)

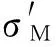
4 算例分析

4.1 一维固结问题的计算

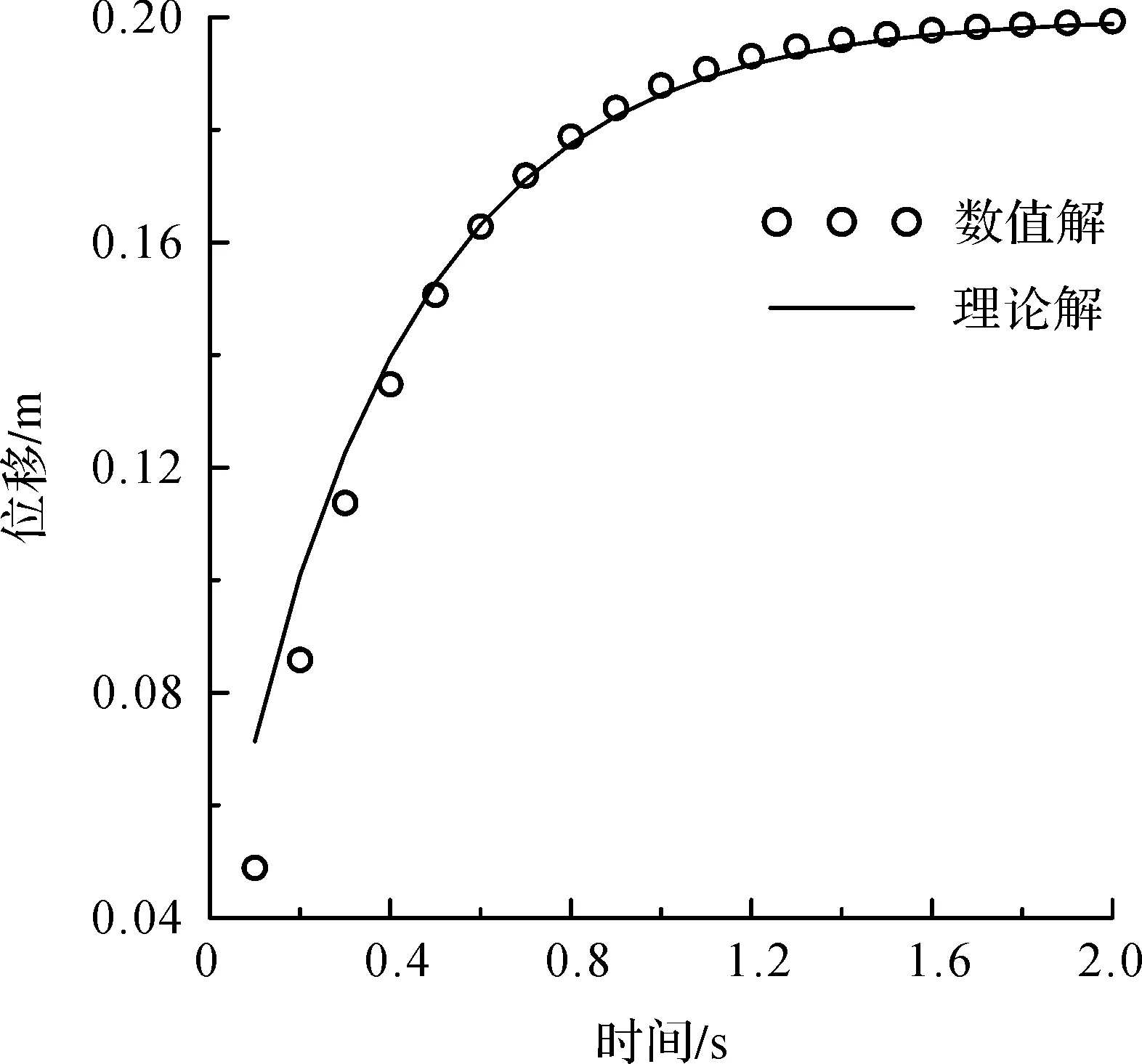
图3 一维固结问题数值解与理论解Fig.3 Analytical and numerical solutions for 1D consolidation problem

首先采用一维弹性固结问题的算例来验证本文方法的准确性。计算一块1 m×1 m的岩体，设定弹性模量E为1 000 kPa，泊松比ν为0，孔隙比e为0.428 6，载荷为顶部均布载荷q为200 kPa，设定顶部为排水边界，其他3个边界不排水。

图3给出了该岩体竖向固结位移随固结时间变化的数值模拟结果，与Terzaghi的一维固结问题理论解对比，二者吻合很好，说明了本文有限元-有限体积混合方法在求解流固耦合问题的准确性。

对于一维固结问题，采用非结构平面四边形网格划分的算例进行计算，如图4所示。在此算例中水平与竖直尺寸分别为5、10 m，2个侧边及底边均为不排水边界，顶部为排水边界，施加荷载为顶部均布荷载。岩体材料弹性模量E为20 GPa，泊松比ν为0.2，孔隙比e为0.4，渗透率k为1 Darcy，水的黏度μ为1×10-3Pa·s，静止土压力系数K0为0.8，材料密度ρ为1.71×103kg/m3。

以计算区域顶端的中点位移为固结沉降的代表值，改变顶部荷载的大小，考察土体最终竖向固结沉降位移与施加荷载大小的关系，并与理论解进行对比。如图5所示，数值计算结果与理论解吻合较好。

图4 一维固结问题算例的网格Fig.4 Grids used in 1D consolidation problem

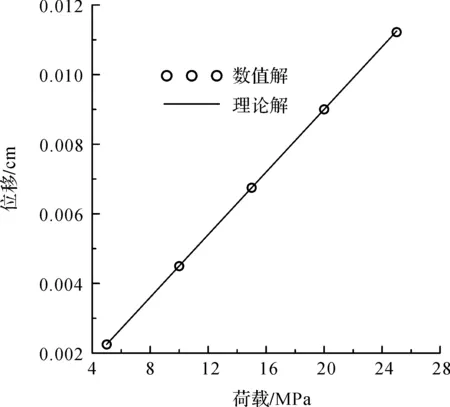
图5 最终固结沉降数值解与理论解Fig.5 Analytical and numerical solutions for final consolidation displacements

4.2 单井生产问题的模拟

对二维单相流体储层的单井定压生产问题进行模拟，取计算区域为一块长5 000 m、深4 000 m向上延伸至地表的区域，储层位于地下3 000 m处，储层厚度约为50 m。采用非结构网格对整个计算区域进行网格划分，如图6所示。计算时约束了两侧的竖向、底边的竖向及水平的位移。

仅设有一口生产井，生产井位于储层的正中部，进行定压生产。算例中对储层内与储层外的区域采用不同的材料参数。对于储层区域，弹性模量E1为20 GPa，泊松比ν1为0.2，孔隙比e1为0.4，渗透率k1为1 Darcy，密度ρ1为1.71×103kg/m3；对于储层以外的区域，弹性模量E2为20 GPa，泊松比ν2为0.2，孔隙比e2为0.1，渗透率k2为1×103Darcy，密度ρ2为1.91×103kg/m3。储层中液相的密度ρf为1.00×103kg/m3，液相的黏度μ为1×10-3Pa·s，静止土压力系数K0为0.8。

随着井定压生产的进行，孔隙压力的降低起初只在生产井的周围出现，最终逐渐发展至整个储层区域，图7给出了生产井定压生产1个月之后储层孔隙压力变化(P-P0)的分布。

图6 单井生产问题的有限元网格Fig.6 Grids used for FEM in single well problem

图7 生产1个月后孔隙压力变化的分布Fig.7 Pore pressure change distribution after one month of production

图8给出了生产1个月后，计算区域内竖向位移的分布情况。可见随着生产井定压生产，整个计算区域出现了明显的变形，而且井单元处竖向位移显著，这反映了实际生产中的井沉降现象。孔隙度和渗透率对应力的敏感性对流固耦合问题的计算结果有着很大的影响。图9给出了考虑应力对孔隙度与渗透率的影响时的生产井产量，可见产量出现了明显的减少。

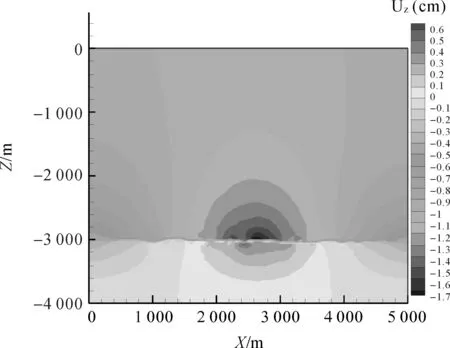
图8 生产1个月后的竖向位移分布Fig.8 Vertical displacement after one month of production

图9 考虑应力对孔渗系数影响时的产量Fig.9 Productions calculated using fixed and stress-dependent porosity and permeability

5 结 论

基于多孔介质力学、渗流力学及u-p假定，建立了渗流与岩体变形耦合问题的基本方程，并采用一种有限元-有限体积混合方法对方程进行离散和求解，此方法对平衡方程与连续性方程分别采用不同的数值离散方法和不同精细程度的网格进行计算，既能保证渗流区域的计算精度，又能够提高计算效率。

一维固结问题的数值计算结果与理论解吻合较好，验证了该方法的准确性。对单井定压生产问题的算例进行了模拟，给出了生产过程中孔隙压力与竖向变形的分布，计算结果表明，当考虑孔隙度和渗透率随应力变化时，定压生产井的产量有明显的减少。

[1] 周志军.低渗透储层流固耦合渗流理论及应用研究[D].大庆：东北石油大学,2003.

[2] 田杰.岩体渗流的流固耦合问题及其工程应用[D].北京：中国科学院研究生院(渗流流体力学研究所),2005.

[3] 董平川,郎兆新,徐小荷,等.油井开采过程中油层变形的流固耦合分析[J].地质力学学报,2000,6(2):6.

[4] EL-AMIN M F, NEGARA A, SALAMA A, et al. Simulation of coupled flow and mechanical deformation using implicit pressure-displacement explicit saturation (IMPDES) scheme[C]//SPE Middle East Unconventional Gas Conference and Exhibition. Abu Dhabi: SPE,2012.

[5] ALPAK F O. Robust fully-implicit coupled multiphase-flow and geomechanics simulation[J]. SPE Journal,2015,20(6).

[6] 刘建军,裴桂红.裂缝性低渗透油藏流固耦合渗流分析[J].应用力学学报,2004,21(1):36.

[7] LI S, LI X, ZHANGhang D. A fully coupled thermo-hydro-mechanical, three-dimensional model for hydraulic stimulation treatments[J]. Journal of Natural Gas Science and Engineering,2016,34:64.

[8] BLANCO-MARTIN L, RUTQVIST J, DOUGHTY C, et al. Coupled geomechanics and flow modeling of thermally induced compaction in heavy oil diatomite reservoirs under cyclic steaming[J]. Journal of Petroleum Science and Engineering,2016,147:474.

[9] REN G T, JIANG J M, YOUNIS R. Fully-coupled XFEM-EDFM hybrid model for geomechanics and flow in fractured reservoirs[C]//SPE Reservoir Simulation Conference. Houston, Texas: SPE,2017.

[10] ANDERSON O, NILSON H M, RAYNAUD X. Coupled geomechanics and flow simulation on corner-point and polyhedral grids[C]//SPE Reservoir Simulation Conference. Houston, Texas: SPE,2017.

[11] EKER E, UZUN I, KAZEMI H. Numerical simulation of dual-porosity multiphase flow using poroelasticity theory[C]//SPE Reservoir Simulation Conference. Houston, Texas: SPE,2017.

[12] TERZAGHI K. Theoretical soil mechanics[M]. London: Chapman and Hall,1959.

[13] BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics,1941,12(2):155.

[14] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. low-frequency range[J]. The Journal of the Acoustical Society of America,1956,28(2),168.

[15] GEERTZMA J. The effect of fluid pressure decline on volumetric changes of porous rocks[J]. Transactions of the American Institute of Mining Engineers,1957,210(12):331.

[16] VERRUIJT A. Elastic storage of aquifers[M]//Flow through porous media. New York: Academic Press,1969.

[17] SAVAGE W Z, BRADDOCK W A. A model for hydrostatic consolidation of Pierre shale[J]. International Journal of Rock Mechanics and Mining Science and Geomechanics Abstracts,1991,28(5):345.

[18] ZIENKIEWICZ O C, SHIOMI T. Dynamic behaviour of saturated porous media: the generalized Biot formulation and its numerical solution [J]. International Journal for Numerical and Analytical Methods in Geomechanics,1984,8:71.

[19] AKAI K and TAMURA T. Study of two-dimensional consolidation accompanied by an elasto-plastic constitutive equation [J]. Proceedings of Japan Society of Civil Engineers,1978,269:98.

[20] OKA F, YASHIMA A, SHIBATA T, et al. FEM-FDM coupled liquefaction analysis of a porous soil using an elasto-plastic model[J]. Applied Scientific Research,1994,52(3):209.

[21] MINKOFF S E, STONE C M, BRYANT S, et al. Coupled fluid flow and geomechanical deformation modeling[J]. Journal of Petroleum Science and Engineering,2003,38(1/2):37.

[22] RUTQVIST J, WU Y S, TSANG C F, et al. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock[J]. International Journal of Rock Mechanics and Mining Sciences,2002,39(4):435,437.