电磁学教与学思路探析*
彭勇宜 何 军 孙克辉 李宏建 郭光华
(中南大学物理与电子学院 湖南 长沙 410083)
大学物理学中的电磁学内容较多,定理和定律多,概念抽象,知识点多,表达式多,记忆难,所占用的学时相比其他课程而言也是较多的.刚开始学习时,学生们普遍以为在中学阶段已经学了很多电磁学知识了,学习电磁学应该很轻松,然而在学习过程中逐渐感觉到不轻松,越来越困难,具体表现在:一是碰到问题后,无法与已学知识点建立联系,没法找到解题思路;二是当学完稳恒磁场、磁介质后,发现内容、概念、表达式突然多了很多,且容易混淆,教师在作业和试卷中经常发现学生写出混乱的表达式,在该写静电场、电介质中的表达式时,却写了稳恒磁场、磁介质中的表达式,该写稳恒磁场、磁介质表达式的时候,却写成了静电场、电介质中的表达式,有时表达式中一部分是静电场和电介质中的,一部分却是稳恒磁场和磁介质中的.电磁学内容全部学完后,思维更为混乱,感觉到内容多,脑海中清晰的只有库仑定律了,其余内容和思维则乱成“一团麻”.在复习时不知从何开始,电磁学知识没有构成一定的逻辑体系.教师在教授电磁学过程中,即使讲解许多例题,最后发现效果不佳,学生遇到新问题仍然束手无策,思路不清晰,无法举一反三.所以有必要对电磁学知识进行梳理,探索分析电磁学中的教与学的思路与线索,找出枯燥抽象的电磁学定理、定律、知识点之间的有机联系,把电磁学知识连成串,形象化、系统化,让它们在师生脑海中从“静止”变成“运动”,让电磁学知识“活跃”起来,让教与学轻松愉快起来,最大限度提高教学效益和教学质量.
1 “点线面体”的思路
电磁学的核心内容,是求解电场强度E和磁感应强度B,按照人类对事物的认识规律,是从简单到复杂的,所以按照点→线→面→体的思路和线索进行教与学,符合人类认知规律,便于复杂问题的求解.电磁学内容和相关问题的求解方法可以通过图1所示的思路和线索很清晰地呈现出来.
在静电场中,求解真空中某个静止点电荷在空间某点产生的电场强度E(r)时,首先是依据实验定律——库仑定律和电场强度的定义式,得到单个点电荷的电场强度E(r)的表达式,然后根据场强矢量的叠加原理,推出多个点电荷构成的点电荷系在空间某点产生的电场强度,其中电偶极子是由两个点电荷构成的特殊点电荷系,可以推出在其延长线上和中垂线上的场强表达式.点电荷系的电荷分布是离散的,接着让电荷连续均匀分布在线上,求解这类“线”问题,是将它还原退化成点电荷场强的求解问题,即采用微元法和场强叠加原理先求有限长带电直线在空间某点产生的场强,再将它推广到求无限长带电直线产生的场的求解问题,也可将有限长带电直线弯曲变形,变成圆环或圆弧,求解他们在圆心处的场强,这些仍是属于带电线产生场强的问题.通过无数个半径不等的圆环叠加可以求解带电圆盘在中心轴线上的场,再推广至无限大带电平面产生的场.也就是将“面”的求解问题还原成“线”的问题,“线”的问题还原成“点”的问题.但在求解无限长圆柱面、球面以及由无数无限长圆柱面叠加成的无限长圆柱体、半径不等的无数球面叠加而成的球体产生的场时,一般不再用微元法了,也就是不把他们还原成线或面,由于它们的电荷分布分别具有轴对称性和球对称性,这时用高斯定理法求解最为简便.无限大带电平面的电荷分布具有面对称性,其产生的场也可用高斯定理快速求出.
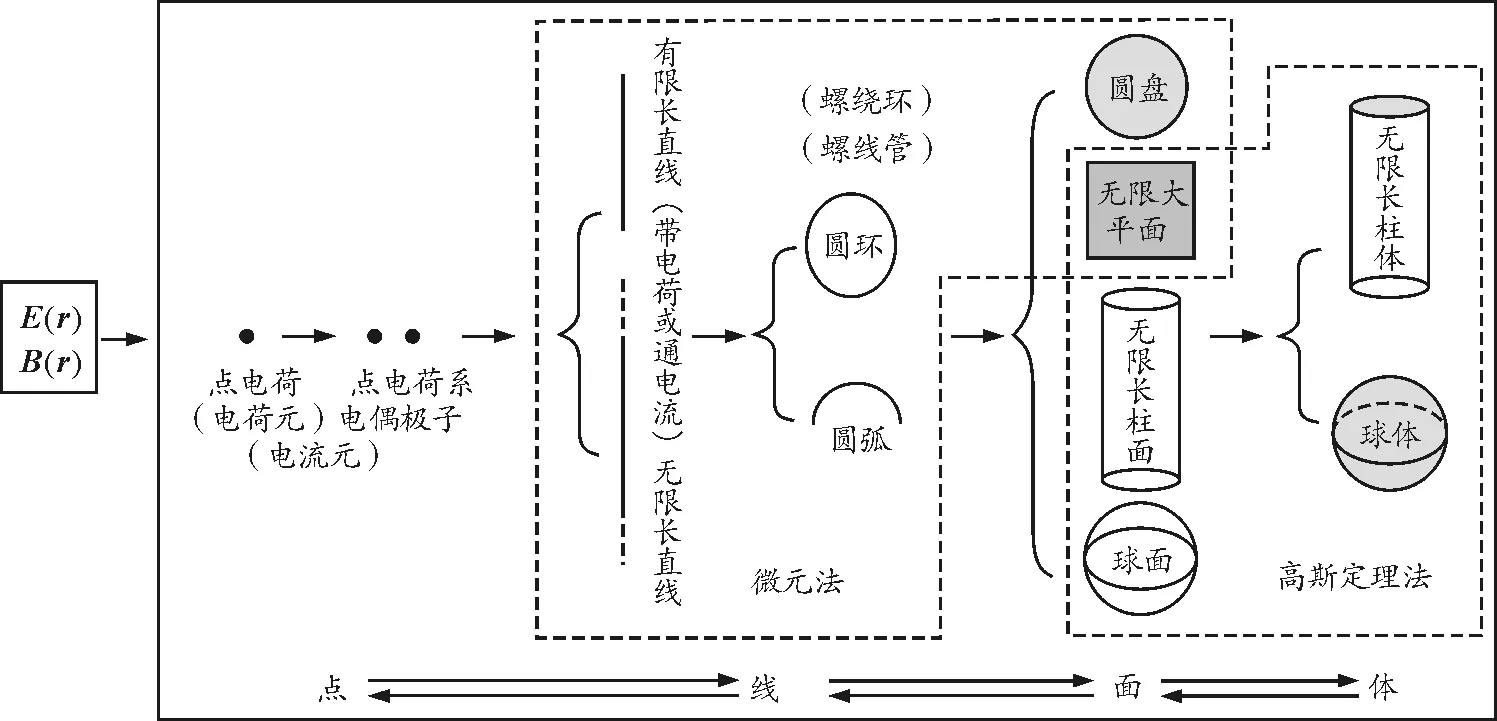
图1 电磁学中的点线面体的思路
在稳恒磁场中,求真空中某点B(r)时,“点”的概念要换成电流元,毕奥-萨伐尔定律在稳恒磁场中的地位也就相当于点电荷或电荷元场强表达式在静电场中的地位了,从毕奥-萨伐尔定律出发,先求载流直导线(有限和无限)产生的磁场,再把它们弯曲变成通电圆环或圆弧,求解通电圆环或圆弧在轴线上的场.许多圆环构成螺线管(有限或无限)和螺绕环,利用圆环的结论求解螺线管(有限或无限)和螺绕环在中心轴线上的场,或把无数载流导线叠加形成载流(平或曲)面,采用微元法或安培环路定理求解它们产生的磁场.由无数载流导线构成无限长载流圆柱面或无限长载流圆柱体产生的磁场,由于电流分布的对称性,用安培环路定理可方便地求解.
由以上分析可知,通过从点→线→面→体的动态变化和从简单到复杂的递进,电磁学中场的求解问题之间的有机联系就显而易见了,求解时就按体→面→线→点的思路进行,将体化简还原成面,面化简还原成线,线化简还原成点的方法进行,即利用已知的简单结论,将复杂问题的求解还原成简单问题的叠加求解,教和学就变得生动有趣了,同时也会激发学生自主学习、自主探索的主动性和积极性.
2 矢量场的两个性质及研究方法形成的思路
电场强度E(r)和磁感应强度B(r)都是矢量,研究矢量场在数学上的方法是求其通量(散度)和环流(旋度),如图2所示,看它们的通量(散度)和环流(旋度)等于多少(图2中“?”号表示的意思).所以就有电场和磁场中的高斯定理和环路定理,至于它们的积分表达式和微分表达式,可以通过高斯公式
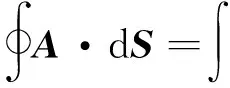
和斯托克斯公式
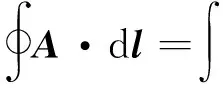
进行转化,麦克斯韦将反映电场和磁场性质的表达式总结起来称为麦克斯韦方程组,也就是指静电场的性质是“有源无旋”,稳恒磁场是“有旋无源”.所以麦克斯韦方程组是高度浓缩的表达式,包含的信息量很大,在教与学的过程中就会发现教材前面所有介绍的内容都是围绕电磁场的性质或麦克斯韦方程组这一中心的引出进行的.所以在复习时,也可以采用与讲授新课内容时相反的顺序,从麦克斯韦方程组这一中心出发逆向往回复习,一直回到电场强度和磁感应强度的定义和求解,麦克斯韦方程组就是这些电磁学知识“树”的“根”,将所有知识点“枝”和“叶”联系起来了.
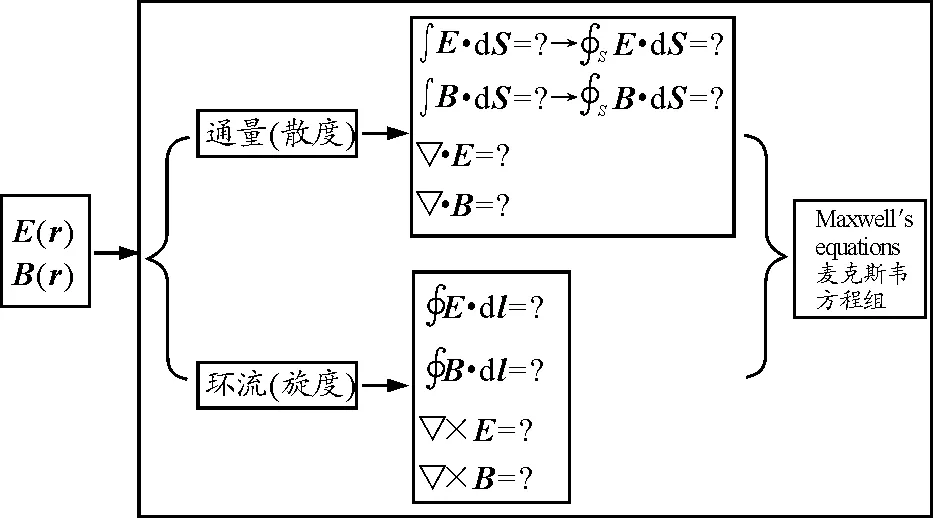
图2 矢量场的两个性质及研究方法形成的思路
3 其余几条贯穿电磁学的思路
电磁学内容前后之间还有几条贯穿在其中的思路和线索,如图3所示,在教与学的过程中必须注意到.先介绍场源离散分布时场的求解,再介绍连续分布时的求解;先介绍真空里场的求解,再介绍介质(或导体)里场的求解,真空也可当作特殊的电磁介质;先介绍静止和不变的场,即静电场和稳恒磁场,再让它们“运动”和“变化”起来(电磁感应部分、电磁场的相对论变换、电磁波等);先单独分别介绍电场和磁场,再介绍它们之间的联系和相互影响(电磁感应部分、电磁介质和场的相互影响);在介绍电磁理论后讲述其应用,电场里大部分教材会介绍电容器(中间为真空或介质),磁场里会介绍霍尔效应、电动机、回旋加速器、磁约束[1,2]等内容,当然有时是先从实验出发,再寻找理论表达式的.在学习静电场和稳恒磁场、电介质和磁介质时采用类比法进行教与学[3~5],会起到事半功倍的效果,特别是在学习磁介质理论里的分子电流观点和磁荷观点时,将相应的物理量和表达式一一进行对比,会加深学生对这些内容的理解,学生就不会感到学习内容越多,就越糊涂、越容易混淆了.明白这些思路和线索后,电磁学内容和逻辑体系就清晰了,教与学也就有了明确的方向和目标.
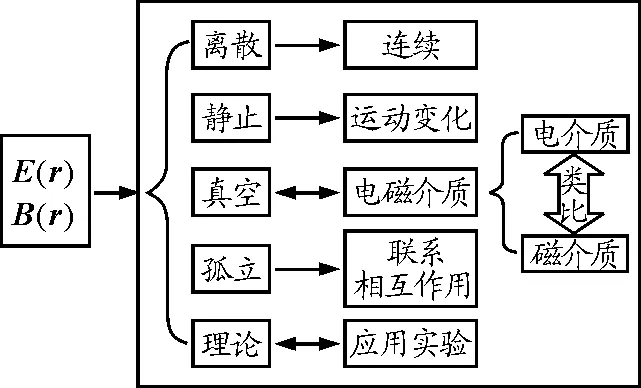
图3 其余几条贯穿电磁学的思路
4 结束语
在电磁学的教与学中,掌握以上贯穿于电磁学中的思路、线索或研究方法后,既可看到电磁学内容这一“森林”全貌,又可看到“树木”,既可看到“树木”的“根”,又可看到“枝”和“叶”,电磁学内容清晰而又系统地反映在这些思路和线索中.这些思路和线索的利用也便于启发式、讨论式、自主探究式教学模式的开展.同时也要认识到这些思路和线索是相互交织的,在教与学过程中必须灵活运用,最大限度提高教学效率和教学质量.
1 赵凯华,陈熙谋.新概念物理教程电磁学.北京:高等教育出版社,2013
2 张玉民,戚伯云.电磁学.北京:科学出版社,2012
3 张宪贵,康艳霜,王云明,等.类比法在电磁学教学中的应用研究.河北农业大学学报(农林教育版),2015,17(3):109~111
4 温耐,王伟锋.类比法在电磁学教学中的运用.物理通报,2013(6):11~12
5 汤维亚.类比法在电磁学教学中的应用研究.高教学刊,2017(2):96~97

