新视角教学RC电路暂态过程
——电路模型等效变换的角度
丘来金 赵 强
(华东师范大学物理与材料科学学院 上海 200241)
RC电路暂态过程是物理类和电气电子工程类课程的基础内容.虽然常见的教材中的分析过程不算非常复杂,然而,在物理模型的构建和物理含义的展现方面,对部分学生来说,仍然存在较大难度,特别是对于大学低年级的学生来说,在学习这部分内容时,容易倾向于通过机械记忆结论来应对考试,阻碍了高层次教学目标的实现.鉴于此,本文将针对教学现状,探讨一种可行的教学改进方略.
现代认知心理学研究的结论表明,在教学过程中,基于学生熟悉的、简单的和直观的现象来构建富有意义的问题分析模型,可以更好地引导学生激活和提取已有记忆,进行富有意义和效果的编码过程,最终实现深层次的记忆重构[1~3].这样,不但有利于快速掌握学习任务,构建稳固的基础知识记忆单元,也有利于在新的任务中快速激活先验图式以及实现相关记忆的扩散式激活,从而较好地实现迁移效果[3,4].
简单的常系数衰减过程对学生来说比较熟悉,是普通物理和高等数学中的基础典型案例.因此,本文首先从简单常系数衰减过程的视角对RC电路暂态过程的简单情形——零输入响应进行分析,然后通过对电容元件的电路模型进行重构变换,对RC电路的全响应进行探讨,直观地展现出该过程的物理内涵,由此实现对教学效果的改善.
1 对RC电路暂态过程的分析
教学RC电路的暂态过程时,常见的典型电路如图1所示.在t=0时刻之前,开关S处于位置1,并且电路已处于稳态.当t=0时,S切换到位置2.
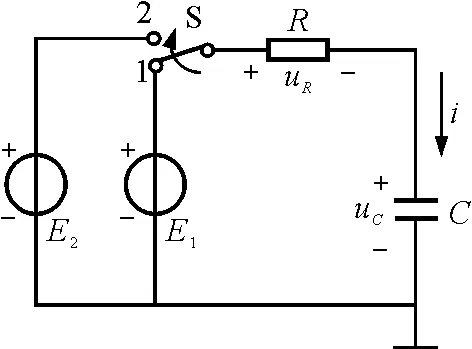
图1 (全响应)RC电路
电路的暂态过程将是由式(1)所描述的全响应,其中,uC的初态(t=0)为E1,终态(t=∞)为E2.
(1)
虽然全响应具有通用性,但是为了分析的方便,先探讨E2=0时的特殊情形.
1.1 E2=0时的零输入响应
E2=0时,电路的暂态过程变为图2所示的零输入响应.由式(1)得到
(2)
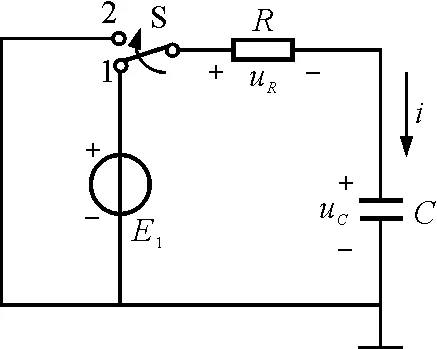
图2 (零输入响应)RC电路
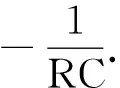
(3)
结果表明RC电路的零输入响应就是电容器初始电压的常系数衰减过程,也就是电容器C中储存的电荷量Q=CuC的一阶常系数衰减过程.
1.2 通过电路模型变换分析全响应
若将电路中的电容器C的电路模型按图3进行等效变换,也就是,将电容器C看作一个电容器C′和一个恒压源E3的串联组合,则有C′=C和uCe=uC-E3.
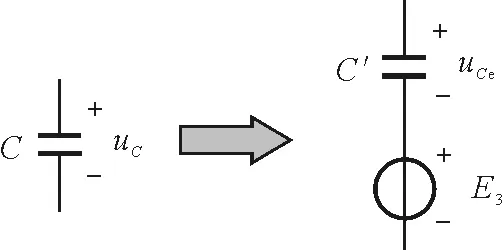
图3 电容器的电路模型等效变换
若E3=E2,图1所示的电路将变成图4所示的情形(在t=0时刻,开关S闭合).由uCe=uC-E2,得uCe|t=∞=0,那么,对uCe而言,该暂态过程是一个与图2相同的零输入响应.因此
(4)
其中ΔE=E1-E2.得出
(5)
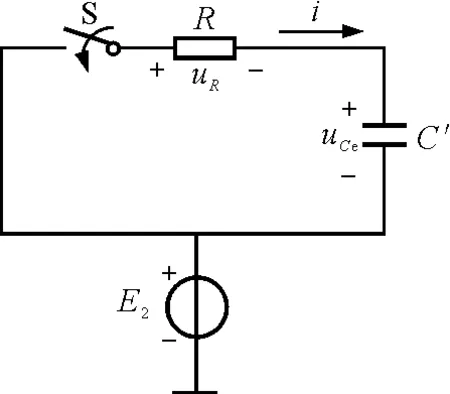
图4 模型变换后的RC电路
由上面的分析过程,可以看出,RC电路的全响应是发生在初态与终态间的一个衰减过程.反映的是初态与终态间电容器两端的电压(或电荷量)差值的衰减过程.
此外,式(5)又可以写为
(6)
可知,全响应可以看作是零状态响应与零输入响应的叠加.对这一结论,在常见的教材中只是简单地解释成因为电容器可以看作一种电源,所以电路符合叠加原理,就可以看作是零状态响应与零输入响应的叠加,然而,在深究时,这一解释又会显得乏力.此外,有些教材通过直接求解式(1)来得出式(6)的结论,并描述为一个自由分量和控制分量的组合.导致很多学生直接记结论,然而,因为缺乏对物理含义的直观诠释,学生在运用该结论解决问题时,难免会有生搬硬套的情形.为此,下面将再次借助电路模型等效变换的途径,来对此加以探讨.
在对电容器部分的电路模型使用图3所示的等效变换时,若令E3=E1,图1所示的电路将变成图5所示(在t=0时刻,开关S闭合).
此时,uCe=uC-E3=uC-E1,可知uCe|t=0=0.
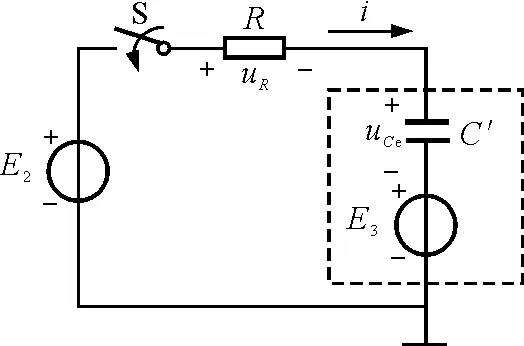
图5 模型变换后的全响应RC电路
根据叠加原理,电路的状态可以看作是图6所示的两个恒压源单独作用时的叠加.那么
uCe=uCe1+uCe2
(7)
那么,根据图3给出的电路模型变换关系和条件E3=E1,则uC满足
(8)
因此,在分析RC电路的全响应时,不是将电容器简单地看作一种电源,而是将电容器初态(储存有能量)时的稳定状态作为参考状态,而此参考状态可以描述为一个恒压源(电动势与电容器的初始储存能量相对应).
当E3恒压源单独作用时,对uCe1来说,是电源电压为-E1的零状态响应,故有
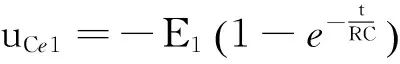
(9)
则
(10)

图6 两恒压源单独作用时的等效电路
其实,根据图3给出的电路模型变换关系可知该电路所示的过程,对uC来讲就是初始状态为uC|t=0=E1的零输入响应,可以直接得出式(10)的结果.
当恒压源E2单独作用时,对uCe2来说,是电源为E2的零状态响应,故有
(11)
则

(12)
可知,该电路所示的过程,对uC来讲,就是电源电压为E2的零状态响应.
至此,由式(8)、(10)和(12)可得
从而得出“全响应=零状态响应+零输入响应”的结论.
2 总结
从上面的分析可以看出,基于学生熟悉的基础知识和技能,通过电路模型等效重构变换的途径,能够直观地展现出RC电路暂态过程的物理实质.在加深对电路模型的掌握的同时,能够较好地帮助学生掌握物理内涵和物理模型构建策略,有效地激活已有的知识记忆,并且建立意义明确的关联,从而实现改善教学效果的目的.
1 Kinjo, H., & Snodgrass, J. G., Does the generation effect occur for pictures.American Journal of Psychology, 2000, 113: 95~121
2 Radvansky, G. A. , Situation models, propositions, and the fan effect.Psychonomic Bulletin &Review, 2005, 12:478~483
3 Anita Woolfolk.Educational Psychology(10thEdition). Pearson Education, Inc. 2007.292~301
4 Richey J. E., Nokes-Malach T. J..Comparing four instructional techniques for prompting robust knowledge.Educational Psychology Review, 2015,27: 181~218

