基于临界B参数的航空发动机压气机喘振监测研究

欧阳运芳，李建兰

（1.上海中航商用航空发动机制造有限责任公司，上海 201306；2.华中科技大学，湖北武汉 430074）

1 前言

喘振是航空发动机压气机的一种非常危险的不稳定工况，如不能及时消喘则有可能导致机毁人亡的严重事故。目前主要采用主动控制和被动控制来预防压气机喘振［1，2］。而喘振监测是控制手段介入的前提。Moore和Greitzer发现压气机系统不稳定状态主要取决于一个无因次参数——B参数，B参数的大小决定了压气机系统是否发生喘振。但目前对B参数的研究并不太多［3，4］。

Yu等发现发生喘振时增大B值或在发生旋转失速时减小B值［5］，Lyapunov指数谱是一条从原点出发的谱线。张杰、黄伟等分别研究了B参数变化对系统状态及压气机气动稳定性的影响［6，7］。Gravdahl和陈策在研究了 B 参数对轴流压气机失速和喘振的影响以及压缩系统中对应的静态分叉行为［8～10］。Hu研究了B参数、级数目以及级负荷增加对喘振的影响［11］。Eyad发现B参数值范围和振荡初始位置条件是确定不稳定行为的决定性因素［12］。Wei利用B参数Hopf分叉理论设计控制律用来对喘振进行主动控制［13］。

综上所述，目前研究主要集中于定性分析B参数大小对压气机稳定性的影响，但缺乏对判断喘振发生的临界B参数的定量研究。因此，本文利用稳定性理论和分叉理论对轴流压气机进行分析，推导临界B参数的表达式，建立全工况下的临界B参数曲面，为航空发动机喘振监测提供依据。

2 压气机稳定性分析

Greitzer和Moore将轴流压气机系统分为上、下游平直管道、带进口导向器的N轴流压气机、集气箱、以及排气管道和排气阀门等部分［3，4］。

假设压气机内的流动是低速、二维流动，扰动速度势为一阶谐波，根据动态压升平衡方程、连续性方程和理想气体定律，可以推导出MG模型［3，4］：

式中 Φ——平均流量系数

Ψ——系统总静压升系数

J——轴向扰动速度幅值的平方

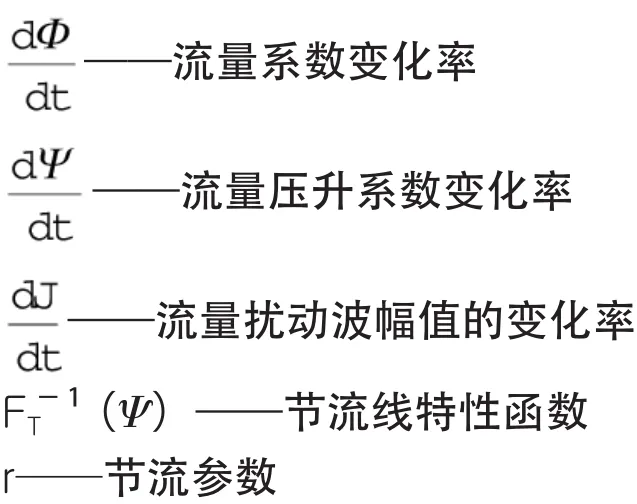
式（1）中B表示压气机系统B参数。B参数是压气机系统在容腔内气体压力和作用在容腔中内力的比值［3］。Greitzer认为B参数的大小决定了压气机不稳定状态是旋转失速还是喘振，当B参数较大时，系统进入喘振状态，但B参数较小时，系统进入旋转失速状态。因此，存在一个临界B参数。

压气机稳态时的流量—压升特性曲线近似为三次曲线，即压气机稳态特性曲线，一般可写成：

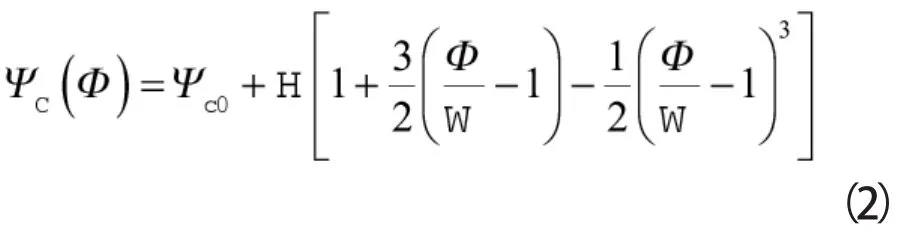
式中 Ψc0——特性线在纵轴的节距

H——特性线的半高

W——特性线的半宽

为分析喘振的影响，令式（1）中J＝0，可以将MG模型简化为二阶微分方程：

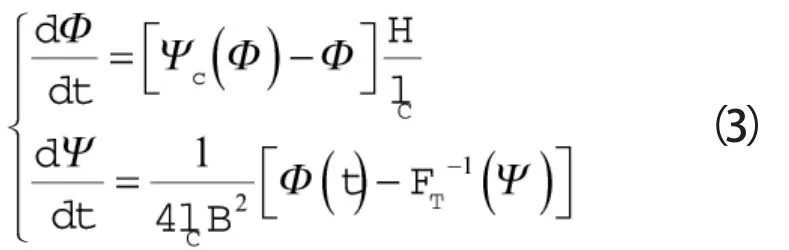
对于一般的二阶微分方程：

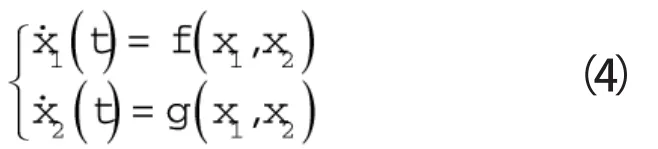
其平衡点为：

则式（4）的雅克比常系数方程为：

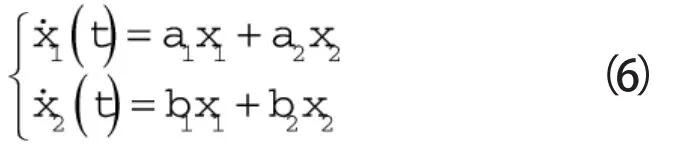
式（6）的系数矩阵为：

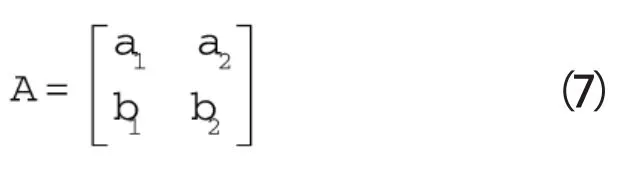
令式（7）的特征方程为：

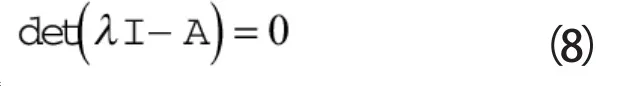
则式（8）的解的一般形式为：

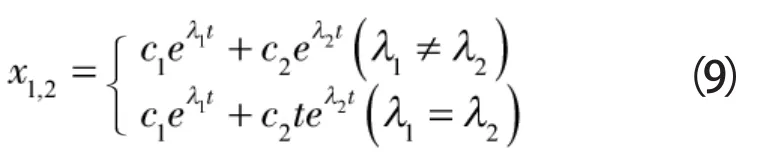
根据稳定性定理：如果在某个邻域内，二阶微分方程的两个解（x1（t），x2（t）），从这个领域内的某个（x1（t0），x2（t0））出发，使得：

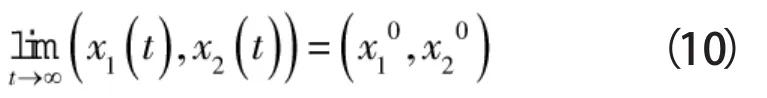
若方程的解满足式（10），则平衡点是（渐进）稳定的，否则，平衡点是不（渐进）稳定的。

因此，对于式（9），只有当λ1，λ2均为负数或均有负实部时，才能满足式（10），该平衡点是稳定平衡点；若λ1，λ2有一个为正数或有正实部时，不能满足式（10），平衡点不稳定。

对式（5）求取雅克比矩阵：

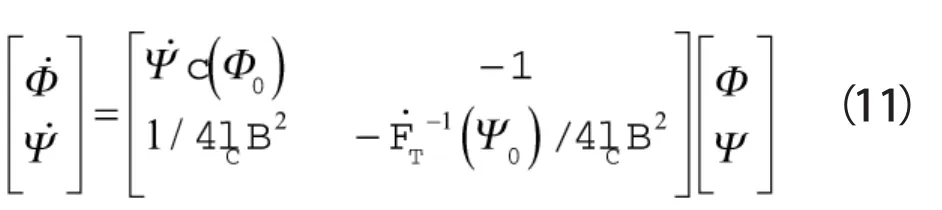
设（Φ0，Ψ0）是系统的平衡点，系统的特征方程为：

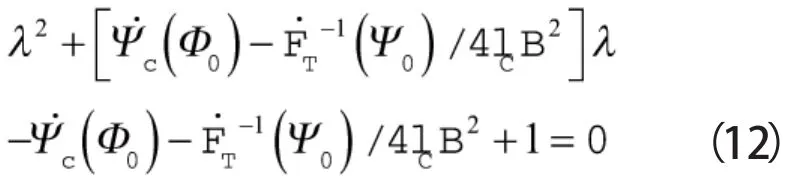
求解特征值方程可以得到：

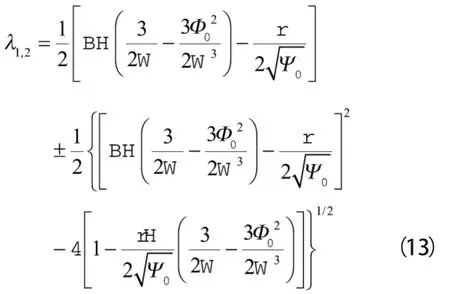
在式（10）中，使λ1，λ2均为负数或均有负实部才能保证平衡点是稳定平衡点。λ1，λ2的大小与特性线、节流参数r和B参数有关。当转速不变时，仅与B参数有关。计算特征值实部随B参数变化的关系，如图1所示。

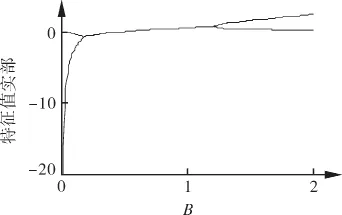
图1 特征值实部随B参数变化

假设其他特征值保持稳定，随着B参数的增大，动力系统的雅克比矩阵的一对共轭特征值穿越虚轴，从左半复平面到右半复平面，在穿越虚轴的时刻，共轭特征值的实部变为零，平衡点的稳定性将发生变化，同时在平衡点产生极限环。这种分叉行为称为Hopf分叉［14］。

图1中B参数作为分叉参数时，当特征值实部从负值向上穿越实轴，即发生了Hopf分叉，也就是喘振开始的时刻。

根据Hopf分叉定理，系统极限环是稳定且唯一的，从稳定性角度来说，出现了极限环即出现了稳定的周期，意味着发生了喘振［10］。因此可以通过Hopf分叉求解喘振发生的临界点，得到临界Bcr参数为：

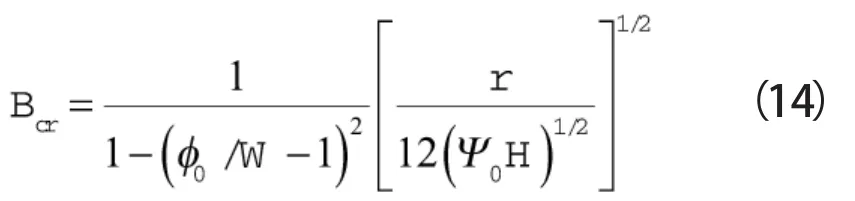
3 全工况临界B参数曲面

根据式（14）及航空发动机压气机实际性能参数，可计算得到压气机的临界B参数，实现对压气机喘振的在线监测。由于作者目前缺乏压气机实际运行数据及实验数据，本文将根据参考文献［3，4］来组织压气机性能参数（如表1所示），以获得压气机的临界B参数。

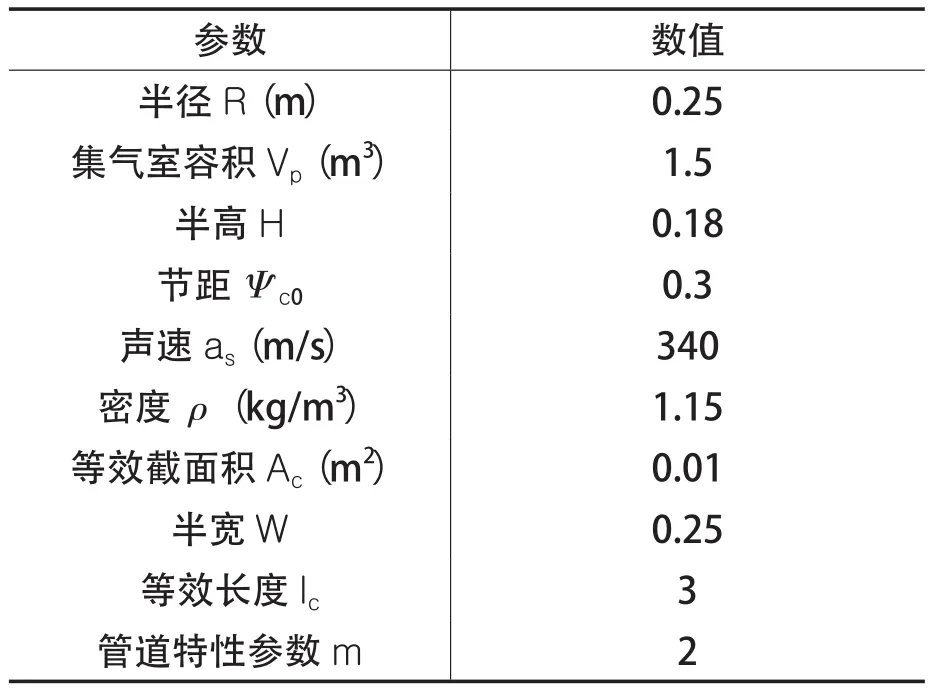
表1 压气机性能参数

节流参数r=0.5时，代入式（14）可以计算出Bcr=0.45，此时转速约为35 m/s。将表1各值代入式（2），可以得到压气机特性线，表示压气机增压能力随流量变化而变化，即压升系数为流量系数的函数。轴流压气机特性线随转速的变化而变化，一般表示成等转速线的形式［15～20］，如图 2 所示，图中每条曲线都代表了一定转速下压升系数和流量系数的函数关系，从下到上依次表示转速从低到高。当转速变化时，H，W值也随之变化。根据文献［19］，转速增大，H，W增大，反之转速降低，H，W减小，且等转速线特性线近似于平行关系。文献资料指出当转速升高时特性线上移，反之特性线下移，可得到一族特性曲线，即等转速特性曲线族。

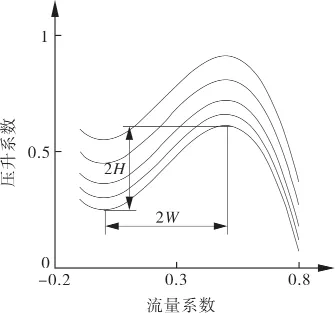
图2 压气机特性曲线

则Bcr与转速U的关系曲线：

影响Bcr另一个重要的参数为节流参数r。对式（14）分析发现，节流参数r越小，Bcr也越小。对于给定的转速U，根据式（14）可得到Bcr与节流参数r的关系曲线：

由式（15）和式（16）可以计算出所有U和r组 合条件下的Bcr值，因此可以得到压气机临界Bcr随转速U、节流参数r变化的三维曲面，即压气机的全工况Bcr曲面图，如图3所示。

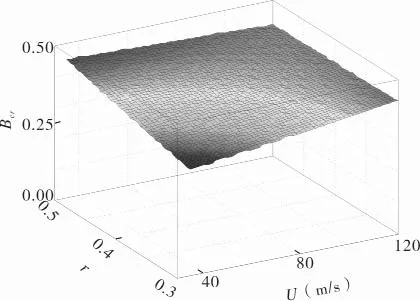
图3 压气机临界Bcr曲面

在图3全工况Bcr曲面中，每一个节流参数r和转速U都对应一个临界B参数。根据上文分析，当系统参数运行在Bcr曲面以下时，系统处于稳定状态或者旋转失速状态，不会发生喘振。因此，对于每一个压气机系统，都可以将运行中将B参数作为一个监控指标，控制节流参数和转子线速度（转速）在一定范围内变化，只要使B参数值处于临界Bcr曲面之下，即可防止喘振的发生。

4 结语

本文提出了一种压气机喘振监测的新方法。在MG模型的基础上，研究了压气机系统平衡点稳定性问题，并利用稳定性理论和Hopf分叉理论推导了临界B参数的表达式，得到了压气机全工况Bcr参数曲面。压气机运行过程中的B参数仅由运行参数决定，运行过程中只要控制压气机的B参数在临界Bcr参数曲面之下，压气机就不会进入喘振状态。该方法不同于传统喘振监测方法，不需要监测压气机的实时流量和压力信号，可为航空发动机压气机喘振的实时监测及预防提供一种新思路。

［1］ 谢彦文，崔耀欣，顾伟，等.压气机喘振机理及防喘措施研究［J］.热力透平，2008，37（2）：94-99.

［2］ 屠宝锋，胡骏，王志强，等.低速轴流压气机旋转失速特性试验［J］.航空动力学报，2009，24（1）：143-149.

［3］ Greitzer E M.Surge and Rotating Stall in Axial Flow Compressors：Part I［J］.ASME Journal of Engineering for Power，1976，98（2）：190-198.

［4］ Moore F K，Greitzer E M.A Theory of Post Stall Transients in Axial Compression Systems：Part I［J］.ASME Journal of Engineering for Power，1986，108（1）：68-76.

［5］ Jiangming Yu，Jiang Zhang，Wei Ding，et al.Study of Lyapunov Exponent Spectra for Axial-flow Compression System［C］.International Conference on Computational Intelligence and Security Workshops，2007：123-128.

［6］ 张杰，屈卫东.非恒定转速下压气机动态模型的建立与仿真［J］.计算机仿真，2013，30（9）：198-202.

［7］ 黄伟，黄向华.紧连阀轴流压气机变转速过失速瞬态模型［J］.航空动力学报，2013，28（7）：1557-1563.

［8］ Gravdahl J T，Egeland O.A Moore-Greitzer axial compressor model with spool dynamics［C］.IEEE Conference on Decision & Control，1998：4714-4719.

［9］ 陈策，李军.基于B参数的轴流压气机过失速稳定性分析［J］.航空动力学报，2004，19（5）：678-683.

［10］ 陈策，聂超群.轴流压气机过失速的非线性动力学分析［J］.航空动力学报，2007，22（9）：1461-1467.

［11］ Hu J，Fottner L.Numerical simulation of active suppression of rotating stall in axial compression systems［J］.Journal of Thermal Science，1996，5（4）：231-242.

［12］ Abed E H，Houpt P，Hosny W M.Bifurcation Analysis of Surge and Rotating Stall in Axial Flow Compressors［J］.Journal of Turbomachinery，1990，115（4）：2239-2246.

［13］ Kang W，Gu G，Sparks A，et al.Surge control and test functions for axial flow compressors［C］.Proceedings of the American Control Conference，1997：3721-3725.

［14］ Chen G R，Moiola J L，Wang H O.Bifurcation control：theories，methods and application［J］.International Journal of Bifurcation andChaos，2000，10（3）：511-548.

［15］ 谭蔚，徐乐，杜怡安，等.基于环境激励的塔器模态参数识别研究［J］.压力容器，2016，33（2）：17-24.

［16］ 周先军，文卫朋，尚庆军.双金属自密封波齿垫片结构参数及密封性能研究［J］.压力容器，2015，32（4）：16-21.

［17］ 郭崇志，周祥，黄巍.工艺参数对铝合金变极性等离子横焊接头的影响［J］.压力容器，2015，32（12）：7-12.

［18］ 安蕾，程小慷.一种多级内啮合航空齿轮泵设计与仿真［J］.流体机械，2016，44（1）：49-53.

［19］ 祝华云，徐志明，胡国军，等.尾缘厚度对压气机叶栅气动性能的影响研究［J］.机电工程，2016，33（2）：187-190.

［20］ 马文通，余南华，苏明.轴流式压气机特性线外推方法［J］.机械工程学报，2006，42（10）：138-141.