基于CURE聚类优化的数据挖掘算法研究

郑志娴，吴为民，李慧敏

(福建船政交通职业学院 信息工程系, 福州 350007)

随着大数据应用逐渐被重视，在大数据的数据挖掘领域产生了众多的数据挖掘聚类算法，其中包括有基于数据密度的聚类算法、基于层次分析的聚类算法、基于数据类型划分的聚类算法等等，各类聚类算法都有其显著的特征，在数据挖掘的某一领域内具有较好的应用效果.例如BRICH算法效率高，适用于凸型或球型聚类类型，对噪声和输入数据不敏感；DBSCAN算法效率一般[1-2]，适用于任意形状的聚类类型，对噪声和数据输入敏感；CURE算法效率较高，适用于任何形状聚类类型，对噪声和输入数据不太敏感；CLARANS算法效率较低，适用于凸型或球型聚类类型，对噪声不敏感对输入数据敏感；CLIQUE算法效率低，适用于凸型或球型聚类类型，对噪声和输入数据不太敏感；K-Means算法效率较低，适用于凸型或球型聚类类型，对噪声和输入数据不太敏感等[3].本文以数据不断增加、数据类型多样、数据结构复杂为研究对象，因此CURE算法具有较好的应用效果，以此为研究对象进行数据挖掘算法优化具有非常现实的意义.

1 CURE聚类算法介绍

CURE聚类算法是一种能够对复杂数据、多类型数据进行高效数据挖掘的算法之一，其在计算过程中将每一个类视为一个点，用点来表示一类的数据，再通过收缩因子对点进行控制使其能够越来越接近类的中心点，因为对数据的封装所以会减少因噪声带来的聚类影响，对聚类的划分更加清晰准确.CURE聚类算法可以对任意类型的数据、任意形状的聚类进行计算，算法效率高，对随时输入数据不敏感，应用范围更加广泛[4].

CURE聚类算法是一个基础的聚类算法，在面对海量数据、结构及其复杂、动态性强和噪声强的数据进行数据挖掘计算时仍存在数据挖掘不准确、数据挖掘效率低得问题[5].CURE算法以类点进行聚类，对聚类对象具有严格的划分，类和类之间的距离计算可采用欧式距离、马氏距离和拉格朗日距离进行计算，但是在数据以不规律形式增加和数据类型复杂多变的情况下，其不能够很好的反映出数据的完整性[6]，从原始数据集中抽取数据会到时数据量庞大计算效率低得问题并且会出现类间距离计算出现误差的问题，由此会导致聚类的结果不准确的现象.因此要使CURE算法能够在数据挖掘中更加灵活，本文提出对CURE算法进行优化，使其具有更加良好的数据挖掘能力和计算效率.

2 CURE聚类算法优化

针对CURE算法在面对海量数据计算优势减弱的问题，本文提出了引入并行化处理数据的方式，将MapReduce函数对不规律动态增加的数据进行并行化处理，以数据对象不确定性为研究目标进行两个类之间的新距离计算方式对CURE算法进行优化，CURE算法优化流程如图1所示.

图1 CURE算法优化流程

对于CURE算法的优化是将所采集到的原始数据划分成为n个数据片，将数据片中的每一个数据作为一个类，计算类与类之间的距离，并将距离最小的两个类合并，计算类间距离过程中引入Map函数实现并行化处理，基于区间数和标准差，Reduce函数更新代表点，计算新类的中心点及代表点，判断聚类数是否满足k=α，若满足则输出聚类结果，若不满足则返回类重新进行距离计算[7-8].

3 基于CURE聚类优化算法的数据

聚类过程分析

3.1 引入MapReduce函数

基于CURE聚类优化引入了MapReduce函数进行数据的并行化处理，利用Map函数将数据集划分成为若干个片，每片的数据分配到不同节点上进行执行.再利用Reduce函数进行分区，根据中间结果的键值划分成R块，以解决CURE算法抽样导致聚类结果又偏差的问题.同时对于不断增加的数据可以在完成并行化处理后快速进行下一时间节点的数据处理.此过程分为Map和Reduce两个阶段，Map阶段将输入的数据进行初始化，使其成为一个类，总数标记为Q，设定聚类个数为k，当Q>k时，距离最近的两个类合并.Reduce阶段根据Map函数的输出，判断Q是否大于k，如果大于则需要继续聚类，如果Q=k，则终止聚类.

3.2 不确定数据类间距离计算

CURE算法类和类之间的距离计算可采用欧式距离、马氏距离和拉格朗日距离进行计算[9-10]，其计算环境是数据量不变，准确知道确定性的数据，可以通过数据值或者界限进行类边界的距离测度度量，而面对不断变化的数据，原有计算方法会出现边界模糊的问题，而导致数据缺失，所以本文提出获取动态数据标准差的方式进行数据处理，对任意两个动态的数据对象Q1和Q2，其之间的变动距离最小值表示为dmin(Q1,Q2)，最大值表示为dmax(Q1,Q2).区间数的计算在给定区间数[X,Y]内的任意距离d为：

d(X,Y)=‖X-Y‖=

(1)

其中：X区间数为X=[XL,XR]，Y区间数为[YL,YR].

利用标准差表示区间，设一组数据X=(x1,x2,……,xn)标准差为：

(2)

用μ表示数据的平均值，数据区间表示为：

Xi=[xi-kσ,xi+kσ](1≤i≤n,k∈R|0≤k≤3)

(3)

用k表示收缩因子，k=1时数据分布在[xi-kσ,xi+kσ]概率为67.5%，k=2时的数据分布在[xi-kσ,xi+kσ]的概率为96.8%，k=3时数据分布在[xi-kσ,xi+kσ]的概率为99.9%，由此确定k的值，将不断变动的数据确定在可接受的概率范围内.

用区间数值表示的数据之间的关系不能够通过相间获取之间距离的关系，所以要通过区间数值的包含、相离、相接、相交来确定位置关系，其中数据的相接关系距离值为0，用代数表示区间数值的距离最大值和最小值分别可表示为：

dmax=|xj-xi|+2kσ

(1≤i≤n,1≤j≤n,i≠j)

(4)

dmin=|xj-xi|-2kσ

(1≤i≤n,1≤j≤n,i≠j)

(5)

用区间表示数据之间的距离：

d(Xi,Xj)=[dmin,dmax]

(6)

3.3 基于CURE聚类优化算法的数据聚类步骤

对数据中的任意两类数据u和v作为基于CURE聚类优化的对象，其中u的中心点为u.mean，v的中心点为u.rep，两个类之间的距离为dist(u,v).数据中的任意两个数据项为p，q，则p和q之间的距离为dist(p,q)，聚类数目为k，CURE聚类优化后的过程表示如下：

通过Map函数对数据进行划分，将挖掘的数据划分为n个数据片，实现由Map函数进行计算的并行化处理；

被Map函数划分的数据片进行聚类，用聚类获得的数据作为一个类，类和类之间的距离表示为d(p,q)=[dmin,dmax]；

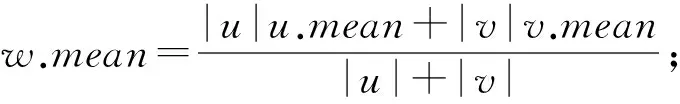
所计算的新类代表点表示为w.rep，用α表示收缩因子α[0.2,0.7]，合并后类的个数变为n-1；

使用Reduce函数对新的数据组进行判断，看是否合并后的类之间达到最优聚类，如果聚类数目未达到预定值，重新进行Map函数计算合并类，如果达到预定值则聚类结束；

删除异常的数据点，完成所有聚类.

4 基于CURE聚类优化算法仿真

实验

4.1 原始数据分布

以某通信企业用户数据为例，数据内容包括用户的基本信息，包括：性别、年龄、类型、行业、业务、付费方式、付费金额、月付费次数、投诉时间、投诉内容、用户等级、用户状态；消费行为信息包括：平均通话次数、本地通话时长、国内长途通话时长、国际长途通话时间、总长途通话时长、漫游通话时长、短信条数、数据流量、其他费用、本次通话时长标准差、国内长途通话时长标准差、国际长途通话时长标准差、漫游通话时长标准差、数据流量标准差、短信条数标准差、其他费用所占比重；用户适用行为信息包括：用户位置、用户网络浏览记录、用户购买记录、用户下载记录、用户上传记录、用户网络流量(d)、用户网络变更、用户机型、业务适用日志.

以该通信企业2017年1～5月份数据作为挖掘对象，随机采集1 000个用户进行数据预处理，通过数据清洗、数据集成得到标准化数据.数据采样时间350 000 h，信息量包含用户通话数据19 445条，短信息3 820条，交互信息284 901条.将预处理后的数据导入Matlab得到原始数据分布图如图2所示.

4.2 数据聚类仿真

利用Matlab按照CURE聚类优化后的方法进行仿真，得到聚类结果如图3所示.

图2 大数据分布

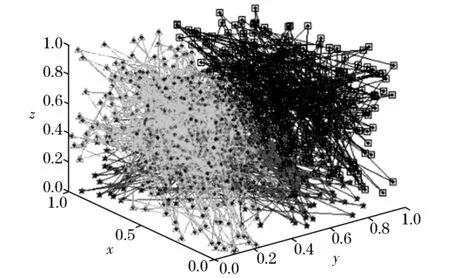
图3 聚类结果

将数据分为3类，获得聚类中心分为为(0.562,0.632,0.305)，(0.625,0.360,0.661)，(0.246,0.475,0.510).

图3中的红色标记为第一类数据，数据具有稳定的变化，通过对数据对应的用户进行分析，通常此部分数据用户为通信公司的稳定客户，平均入网时间在3 a以上，年龄层在30～40岁之间，具有稳定的收入，能够保持月通话时间在300 min以上，长途通过时间较长，通话时间段，投诉较少，对话费不敏感.此类用户是该通信公司的优质客户，具有较好的忠诚度，若非突发事件，不会对公司业务造成较大的不稳定因素，是长期稳定维护基础用户.

图3中的绿色标记为第二类数据，数据具有不稳定变化特征，通过对数据对应的用户进行分析，通常此部分数据用户为通信公司新入网用户，平均入网时间在6个月以下，每次缴费金额在50元以下，月通话时长50 min以下，长途通话较少.此类用户对于通信公司来讲属于低价值用户，用户黏度较低.

图3中的蓝色记为第三类数据，数据具有间歇变化特征，该部分用户入网时间一年以上，每次缴费金额在100～200之间，月通话时长100～200 min.此类用户为通信公司潜在用户，具有较大的培养空间.

4.3 数据聚类结果分析

通信企业部分数据聚类结果如表1所示.

表1通信企业部分数据聚类结果

数据分类 用户序号一类数据2、4、6、8、10、12、14、16、18、110、121、132、143、154、165、176、187、198、201、311、450、550、750、850、950、1000二类数据31、32、33、34、35、36、37、38、39、40、45、55、65、75、85、95、100、111、122、133、144、155、166、177、188、199、200、301、302、405、406、505、506、606、707、808、909三类数据1、3、5、7、9、11、13、15、17、19、41、42、43、44、46、47、47、49、50、51、52、53、54、56、57、58、59、115、116、117、211、212、214、315、316、415、416、517、519、619、717、719、818、891、914、999

通过通信企业部分数据聚类结果可以清楚的划分出每一位用户所归属的分类，由此可对不同类型用户进行针对性的服务和管理.对于不同类型数据的分析可了解到通信企业用户对公司品牌的信赖程度，若一类数据量较大则证明该企业具有稳定的用户资源，一类数据增长则该公司的发展处于稳定增长期.若二类数据量较大，则证明该企业仍较为年轻，用户资源稳定性不高，二类数据增长则是该公司在短期内的营销手段起到了一定的效果，后续应调整业务结构使用户成为企业忠实用户.若三类数据量较大，则证明该企业已经有了一定的客户基础，需要对用户进行更好的维护使潜在用户成为忠实用户.由表1可以看出该企业目前二类和三类数据量较多，证明企业正处于高速的发展期，企业应针对该时期制定针对性的业务，使用户成为企业忠实的用户资源.

从通信企业用户数据中抽取n组数据，进行CURE聚类优化前后时间上的对比，结果如表2所示：

表2CURE聚类优化前后时间对比结果

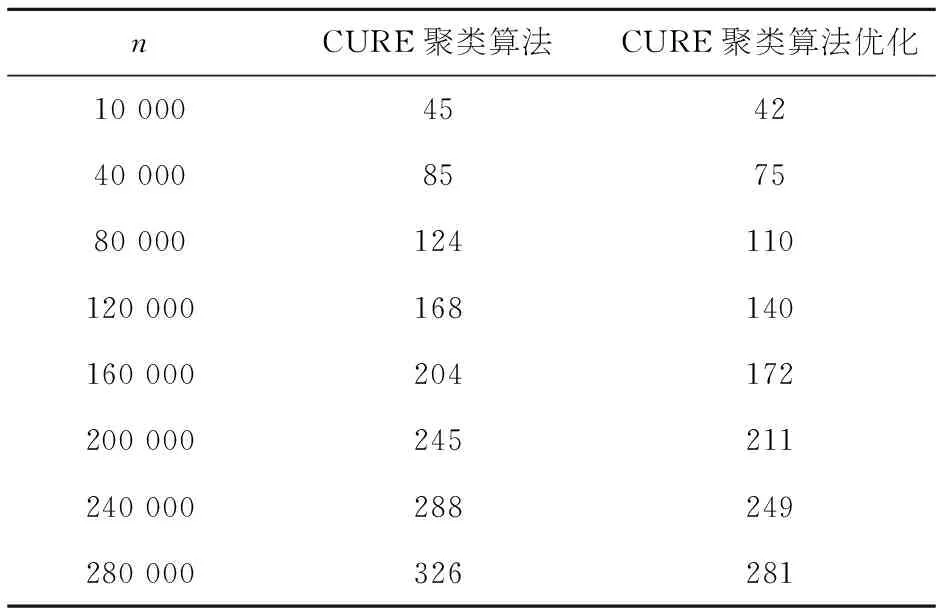
nCURE聚类算法CURE聚类算法优化10000454240000857580000124110120000168140160000204172200000245211240000288249280000326281

由表2可见，CURE算法本身在不确定数据的聚类时间上不具有优势，但是经过优化后本文所提出的CURE算法优化在聚类时间上具有了明显的优势，这也证明了此次算法的改进在聚类时间上具有较好的实用性.

再进行算法准确的比较如表3所示.

表3CURE聚类优化前后准群性对比结果

nCURE聚类算法CURE聚类算法优化10000659940000759580000609212000058911600005491200000759024000078892800005688

由表3可见，随着数据量的增加，CURE算法自身的稳定性较差，优化后稳定性明显提高，而且准确率大幅度提升.

5 结 语

在互联网数据爆发式增长，移动设备产生数据量不断增加，网络数据复杂度不断深化的过程中，对数据的挖掘难度日益的加大，而面对不断增长和变化的数据原有的数据挖掘算法显然无法满足数据复杂与多变的挖掘需求，因此本文通过比对分析后对基于CURE聚类算法进行优化使其在一定程度上满足变动数据挖掘的需求，介绍CURE聚类算法的基本原理和优化方法，并阐述基于CURE聚类优化算法的数据聚类过程，包括引入MapReduce函数，计算不确定数据间距离，采用距离区间数的方式解决边界模糊问题，提高变动数据距离计算的准确性，梳理基于CURE聚类优化算法的数据聚类步骤.通过以某通信企业不断变化的用户数据进行仿真实验，该数据可划分为三大类，一是用户基本信息，二是用户消费行为，三是用户操作行为，三种变动类型数据通过数据预处理后倒入Matlab得到原始的数据分布图，再通过CURE聚类优化算法进行聚类仿真得到仿真结果，试验证明了本文提出的以范围约束计算变动数据类，能够较好的对数据进行挖掘，提了高数据挖掘的准确性和数据挖掘的效率.

[1] 齐兴斌，赵 丽，李雪梅.基于BIRCH聚类加速的彩色图像增强算法[J].计算机测量与控制,2016,24(4):137-140.

[2] 向柳明，周渭博，钟 勇.基于高斯过程的CLIQUE改进算法[J].计算机应用,2015(s2):85-87.

[3] 张晓琳，崔宁宁，杨 涛，等.一种分层自适应快速K-means算法[J].计算机应用研究,2016,33(2):421-423.

[4] 李 松，崔环宇，张丽平，经海东.基于CURE聚类算法的静态R树构建方法[J].计算机科学,2015,42(10):193-197.

[5] 高长元，王海晶，王 京.基于改进CURE算法的不确定性移动用户数据聚类[J].计算机工程与科学,2016,38(4):768-774.

[6] 王寅同，王建东，陈海燕，等.一种代表点的近似折半层次聚类算法[J].小型微型计算机系统,2015,36(2):215-219.

[7] 倪志伟，荆婷婷，倪丽萍.一种近邻传播的层次优化算法[J].计算机科学,2015,42(3):195-200.

[8] 王志春.初始中心点优化的K-means聚类模型[J].电脑迷,2016(9):50-51.

[9] 伍育红.聚类算法综述[J].计算机科学,2015,42(s1):491-499,524.

[10] 陈 晓，赵晶玲.大数据处理中混合型聚类算法的研究与实现[J].信息网络安全,2015(4):45-49.