基于RTWT平台的控制力矩陀螺LQR方法研究
钱玉恒, 王佳伟, 杨亚非
( 哈尔滨工业大学 航天学院 飞行器控制实验教学中心, 哈尔滨 150001)
当今世界,航天技术飞速发展,航天器的用途种类愈加繁多,规模愈加扩大,航天器的精度与稳定性需要随之提高以达到航天工程领域的要求,而其姿态稳定性更是这一切的前提.航天器的姿态控制一般采用控制力矩陀螺(Control Moment Gyroscope,简称CMG)作为它的执行器[1-4],例如,国际空间站应用的一些单框架力矩陀螺或双框架力矩陀螺,需要配置力矩陀螺的构型,使多个陀螺可协同动作,进而实现姿态控制的作用.控制力矩陀螺基本原理是通过改变陀螺飞轮的转轴方向,产生角动量交换,并作用到航天器上,达到改变其角速度及姿态的目的[5].据不完全统计,在国际航天领域应用中,现在有近400个航天器采用控制力矩陀螺作为其姿态控制系统的主要执行器.在国内,天宫一号飞船则第一次使用了控制力矩陀螺作为其执行机构[6],并且进一步应用到了天宫二号上[7-10].目前,针对控制力矩陀螺的有关研究取得了很多的成果[11-12],这些研究将为航天器姿态控制理论的学习奠定必要的基础.美国ECP公司生产的Model750型控制力矩陀螺是一种能够全面验证力矩陀螺特性的实验装置,已经在世界众多知名大学得到应用,促进了对力矩陀螺的研究和教学.
RealTime Windows Target(简称RTWT)是基于Matlab软件的实时实验平台,利用Simulink构建的控制器,通过运动控制卡对硬件系统进行实时控制,从而构成半实物的实时控制研究.
本文首先将介绍控制力矩陀螺的结构,推导其数学模型,然后利用实时仿真平台,基于线性二次调节器(linear quadratic regulator,简称LQR)方法为其设计最优控制器参数,并进行仿真验证.
1 设备组成
该实验装置由机电装置、控制箱和应用程序组成[8].
控制力矩陀螺的机电部分如图1所示.主体包括4个部件:框架A、B、C和转子D.框架A绕轴4旋转,角位置由编码器4测量;框架B绕轴3旋转,角位置由编码器3测量;框架C绕轴2旋转,角位置由编码器2测量.另外,为每个框架分别配置了摩擦滑环,惯性开关和制动器.转子D是大惯量转子,绕轴1旋转,由直流伺服电机1驱动,角位置由编码器1测量.

图1 控制力矩陀螺机电部分
控制系统处理器使用M56000系列,能够在高采样率下执行控制律,可以分析解释程序指令,并支持数据采集,轨迹生成,系统状态及安全检测等.
用户界面可以实现控制器设计、轨迹定义、数据采集、绘图系统、执行指令等功能.内置的编译器通过数字信号处理器进行程序代码的传送和执行.该接口支持多种功能,提供了一个非常强大的实验环境.
2 数学模型推导
建立一组坐标系如图2所示,其中:ai,bi,ci和di(i=1,2,3)为相互正交的单位向量,并且分别固定在框架A,B,C,和D上,组成四个固连坐标系,对应的四个转动轴为轴4,轴3,轴2,轴1.单位正交向量Ni(i=1,2,3)构成惯性参考坐标系N.q1定义为D在d2方向的角位移,q2、q3和q4被定义相应的转角,它们决定了系统构形.另外,在动力学分析中,考虑系统的质心位于转子D中心,不考虑转子的移动,通常只考虑D的角速度ω1给出系统部件的主惯性矩阵如下:

图2 坐标系
(1)
其中,Ix,Jx,Kx(x=A,B,C,D)分别表示部件A,B,C和D中绕第i(i= 1,2,3)方向的标量转动惯量.A在N中的角速度给出如下:
NωA=ω4a3
(2)
同理,我们定义以下量:
AωB=ω3b2
(3)
BωC=ω2c1
(4)
CωD=ω1d2
(5)
将广义坐标与角速度相关联的运动学微分方程如下:
(6)
(7)
(8)
将每个部件的坐标系变换到惯性坐标系:
(10)
(11)
(12)
c2=d2
(13)
该装置具有两个输入:第一个输入是旋转电机,施加的转矩T1,则C和D的转矩为:
TD=T1d2
(14)
TC=-T1d2
(15)
第二个输入转矩T2,则C和B的转矩为:
TC=-T2c1
(16)
TB=-T2c1
(17)
系统的动力学模型可由式(1)~(17)描述.再求解其运动方程:
T1+f1(q2,q3;ω2,ω3,ω4;ω1,ω3,ω4)=0
(18)
T2+f2(q2,q3;ω1,ω3,ω4;ω1,ω2)=0
(19)
f3(q2,q3;ω1,ω2,ω3,ω4;ω1,ω3,ω4)=0
(20)
f4(q2,q3;ω1,ω2,ω3,ω4;ω1,ω2,ω3,ω4)=0
(21)
定义系统的平衡点为ω1=Ω,q2=q20,q3=q30,则线性化方程为

(22)
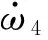
(23)

(24)

(25)
至此,系统的数学模型完全得出.
3 控制力矩陀螺的RTWT平台
在RTWT平台下,搭建控制力矩陀螺的控制框图,如图3所示,其中,深蓝色模块代表实际的物理对象,即使用ECP软件编写好的用于实时控制的板卡模块;黄色模块表示输入量,其内部有六个不同的输入信号与信号六接口信号选择器相连;浅蓝色的模块表示控制器,需要根据实际的控制器来设计,其结构要根据实际控制系统的结构进行改变和重新搭建.

图3 控制力矩陀螺的RTWT实时控制框图
4 LQR实时控制器的设计与控制实验
LQR理论是现代控制理论中发展最早、最成熟的一种状态空间设计方法,利用LQR可得到状态反馈的最优控制规律,易于构成闭环最优控制,可让系统满足一定的性能指标要求.
4.1 实验装置构形及简化数学模型
在本实验中,实验装置的配置构形如图4,运动示意图如图5.
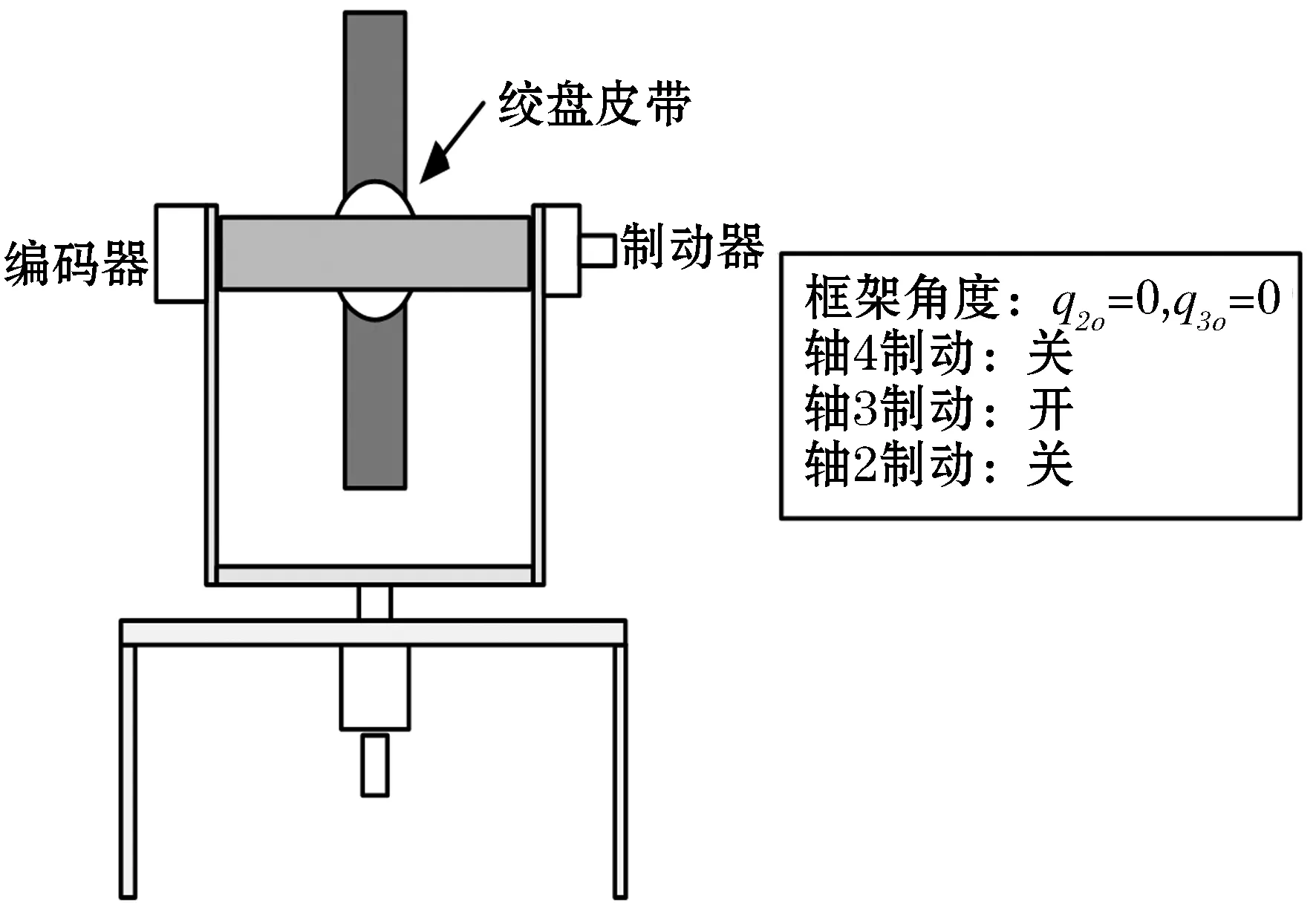
图4 Model750构形图

图5 运动形式示意图

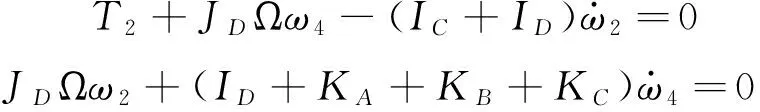
(26)
对于原系统的七个状态变量(q2,q3,q4,ω1,ω2,ω3,ω4)(转子角位置q1无实际意义,为底座轴),控制目标是框架A(即轴4)的位置,因此首先选择两个状态变量q4和ω4,另外关于主控制轴4与输入力矩T2的传递函数为三阶,由于此时框架3被锁定,q3,ω3均为0,且转子D的速度是单独控制,而框架A是通过电机2,即框架C(轴2)间接驱动的,因此选择框架C的角速度ω2作为第三个状态,综上系统的状态变量X=[q4ω2ω4]T即可得到控制陀螺力矩的状态空间模型:
(27)


(28)
其中系统矩阵根据装置的参数可得

C=[1 0 0]
为其构造二次型目标函数如下
(29)
其中
(30)
接下来通过全状态反馈使得二次型目标函数J最小.利用Matlab中介黎卡提方程的命令lqr(A,B,Q,R),求解控制矩阵K.画出LQR控制的框图.见图6、7.

图6 时域LQR控制框图

图7 频域LQR控制框图
根据图7,可得闭环传递函数:
(31)
其中:
(32)
N2(s)=ke2ku2(ID+KA+KB+KC)s
(33)
N4=-ke4ku2ΩJD
(34)
(35)
(36)
4.2 控制器参数设计
选定状态反馈控制律
u=-Kx
(37)
其中:K=[k1K2K3].通过求解黎卡提方程寻找使目标函数最小的控制器K,即
(38)
经过多次实验和参数改良,取r=0.05.综上求得K=[-4.5 0.072 -0.22].令输出等于输入求得kpf=-4.5
4.3 LQR实时控制器搭建
LQR实时控制器的搭建结构如图8所示,k1和k3所在的环节均与编码器4相连,表示轴4位置的反馈信号,k2所在回路与编码器2相连,表示轴2的反馈信号.由此对应状态变量x,构成了一个LQR全状态反馈控制器.

图8 RTWT平台
4.4 控制实验状况
在控制力矩陀螺硬件平台中设置采集编码器2,编码器4,命令位置1和控制效果1的数据;在RTWT平台中,给定一个幅值为10 V,停留时间为4 s,重复次数为1的阶跃信号;在控制器单元输入设计的LQR控制器参数,编译并加载到硬件平台中,得到阶跃响应和频域响应曲线如图9、10.

图9 阶跃响应曲线

图10 频域响应曲线
经过测量计算时域响应曲线的峰值时间为0.297 s,超调量为3%.因此,可以看出LQR方法设计的控制器具有很快的上升时间(假设没有饱和),和更宽的带宽(仅限于当前参数).同时经过对K值参数的不断调整和控制,得到如下结论:k1(绝对值)的取值会直接影响到控制系统的峰值,过大则会造成过高的超调;k2(绝对值)的取值过大会使系统的阻尼过小,系统发生谐振;k3(绝对值)也会对系统阻尼造成直观影响,过大则系统快速性降低,过小则会发生过多的震荡.因此,还应根据黎卡提方程所求的K矩阵进行微调,取最理想结果.
5 结 语
本文主要利用实时实验系统平台为ECP750控制力矩陀螺装置设计了LQR实时控制器,实现了最优的状态反馈控制.通过这个实验,学生可以掌握高级的控制方法在控制力矩实验装置中的实践应用.
[1] 吴 忠,张激扬. 控制力矩陀螺框架伺服系统动力学建模与控制[J]. 应用基础与工程科学学报,2007,15(1):130-136.
[2] SERAJI H. Configuration Control of Redundant Manipulators: Theory and Implementation[J]. IEEE Transactions on Robotics and Automation,1989,5(4):472-490.
[3] 汤 亮,贾英宏,徐世杰. 使用单框架控制力矩陀螺的空间站姿态控制系统建模与仿真[J]. 宇航学报,2003,24(2):126-131.
[4] 张锦江,李季苏,吴宏鑫. 用单框架控制力矩陀螺的大型航天器姿态控制系统实物仿真研究[J]. 宇航学报,2004,25(4):382-388.
[5] 吴 忠,魏孔明. 基于非线性观测器的控制力矩陀螺操纵律设计[J]. 北京航空航天大学学报,2006,32(11):1295-1298.
[6] 张志方,董文强,张锦江,等. 控制力矩陀螺在天宫一号目标飞行器姿态控制上的应用[J]. 空间控制技术与应用,2011(6):52-59.
[7] 陈 璐,袁建平. 基于双框架变速控制力矩陀螺的航天器姿态控制研究[J]. 电子设计工程,2014(23):114-117+122.
[8] 王佳伟,杨亚非,钱玉恒.基于PID方法的控制力矩陀螺控制器设计[J]. 实验技术与管理,2015,32(4):92-97.
[9] 王佳伟,杨亚非,钱玉恒. 基于控制力矩陀螺的进动性和章动性实验[J]. 实验技术与管理,2015(8):50-54.
[10] 王一琳. 天宫飞天的“定海神针”—记天宫二号控制力矩陀螺[J]. 中国航天,2016(11):16-17.
[11] 张科备,王大轶,汤 亮. 基于增益调度的变速控制力矩陀螺操纵律设计[J]. 空间控制技术与应用,2016(6):31-36.
[12] 邓瑞清,刘 刚,赵 岩,等. 控制力矩陀螺干扰传递模型的分析与实验研究[J]. 光学精密工程,2017(2):408-416.

