线扫描相机标定及畸变矫正方法
朱瑶 王治乐 贺磊 周程灏
线扫描相机标定及畸变矫正方法
朱瑶 王治乐 贺磊 周程灏
(哈尔滨工业大学航天学院,哈尔滨 150001)
线扫描相机由于其高分辨率以及高数据处理效率的优势,使得其在测量领域的应用越来越广泛。但线扫描相机也会因光学系统畸变的存在影响成像的几何位置精度,造成图像的失真。文章面向线扫描相机标定及畸变矫正的应用需求,提出一种将一维数据映射到二维数据而不改变原始数据的方法,以利用面阵相机的标定方法来标定线扫描相机。在标定过程中,采用新型的标定板来创建世界坐标系与图像坐标系之间的关系。文章利用数字图像处理的方法,对光学镜头自身畸变进行标定和矫正,基本消除了由于图像变形而产生的测量误差,有效解决了由于镜头畸变而降低图像中物体的几何位置精度的问题。
图像处理 相机标定 畸变矫正 线扫描相机
0 引言
由于线扫描相机具有获取数据准确性好、效率高等优点,因此,其用于测量的应用变得越来越重要,尤其当物体较大、连续移动或需高分辨率成像时,线扫描相机有着不可替代的优势[1-5]。为了对大型零件的变形和大空间内物体的运动状态进行实时监控,大视场高精度的线扫描相机应运而生。该类相机可以应用于航天飞行器试验、飞机结构强度静力/疲劳试验、大型雷达测量等领域,并且满足高精度动态测量的需求,还可以推广到造船、电力、建筑、交通等领域的大型零件测量应用中[6]。
然而,由于光学系统设计、光学镜头的制造误差和装调误差等因素,造成物体在经过光学系统后实际所成的像与理想像之间存在不同程度的非线性几何畸变[7-10]。而且,光学镜头不同视场的畸变也不同,边缘视场的畸变最大。畸变的存在直接影响成像的几何位置精度,在视场比较小的光学系统中畸变不显著,但大视场的光学系统就必须采取措施来消除畸变带来的影响[11]。
要想对光学系统进行畸变矫正,首先需要对光学系统进行标定。目前基于面阵相机的标定方法已有很多,如:文献[12]提出了一种用于机器视觉测量的相机标定技术,采用两步法获取摄像机的外部参数、焦距、径向畸变以及图像扫描参数;文献[13]提出了一种灵活的方法来标定相机,此方法仅需要相机获取几个(至少两个)不同方向的平面图案,并使用基于最大似然准则的非线性优化技术,得到解析解,方法灵活且容易实施,测试数据也非常好。目前对于线扫描相机的畸变校正方法很少被提及。线扫描相机获得的是一维图像信息,通常比二维面阵相机测量更精确有效,并且可以更简单方便地对获取图像进行处理。面阵相机是基于二维图像进行标定的,而线扫描相机只能获得一维图像,因此,面阵相机的标定方法并不适用于线扫描相机。本文所述的线扫描相机标定方法实现了一维到二维图像数据的转换,能够通过坐标转换建立世界坐标系与图像坐标系的关系,从而实现线扫描相机的标定以及畸变矫正。
1 线扫描相机图像采集系统
线扫描相机其CCD/CMOS传感器由单线感光元件构成,与拍摄二维图像的面阵传感器相机不同,如图1所示。虽然传感器只有一个像素高,但可以足够宽,以一定速度移动物体或相机逐行获取图像,最终获得一幅二维图像。线扫描相机具有比面阵传感器相机更好的测量精度,且线性传感器通常具有比面阵相机高的分辨率。当物体较大,连续移动或高分辨率成像时,线扫描相机通常是比面阵相机更好的选择[13]。
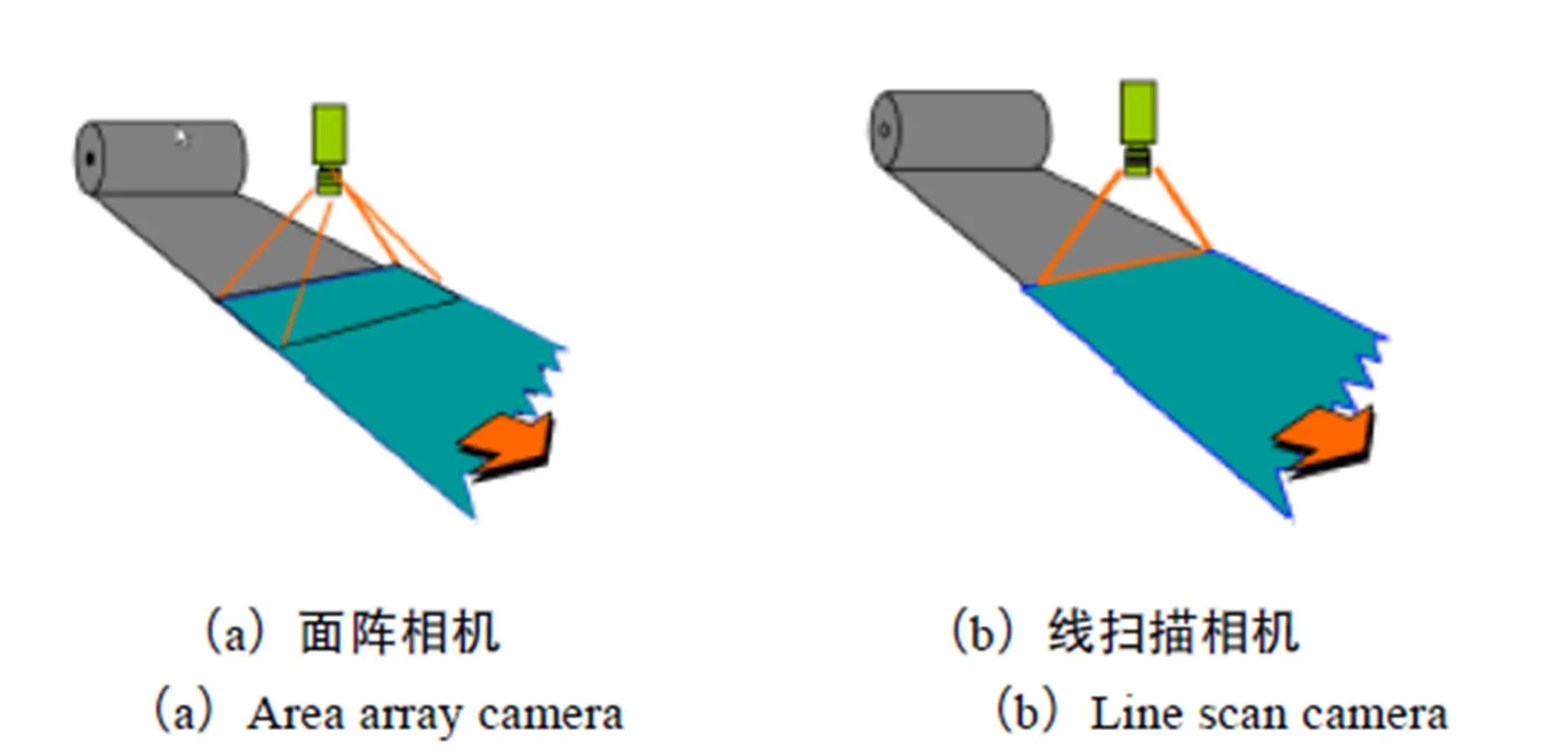
图1 面阵相机与线扫描相机
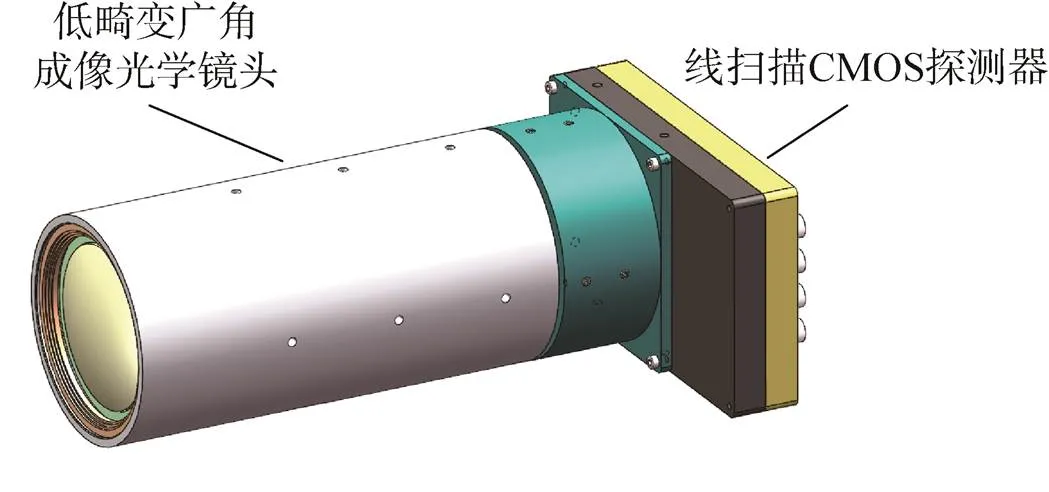
图2 光学系统结构
图2为光学系统结构示意图,是由低畸变广角成像光学镜头、线扫描CMOS探测器组成的光机电一体化产品。线扫描CMOS探测器组件与低畸变广角成像光学镜头固定在一起,光学镜头将搜集到的可见光图像清晰成像在探测器焦面上。探测器通过光电转换,生成相应强度的电信号输出,生成可见光图像,供后续图像处理,从而实现大视场、高清晰、远距离目标观测及图像采集功能。
具体的光学系统技术指标如下:
1)工作波段:480~650nm;
2)视场角:≥90º;
3)光学畸变:≤5%;
4)工作距离:3~100m;
5)MTF≥0.4(0视场,100线对/mm),MTF≥0.3(0.7视场,100线对/mm);
6)工作温度:–10℃~+70℃;
2 相机标定
2.1 制备标定板
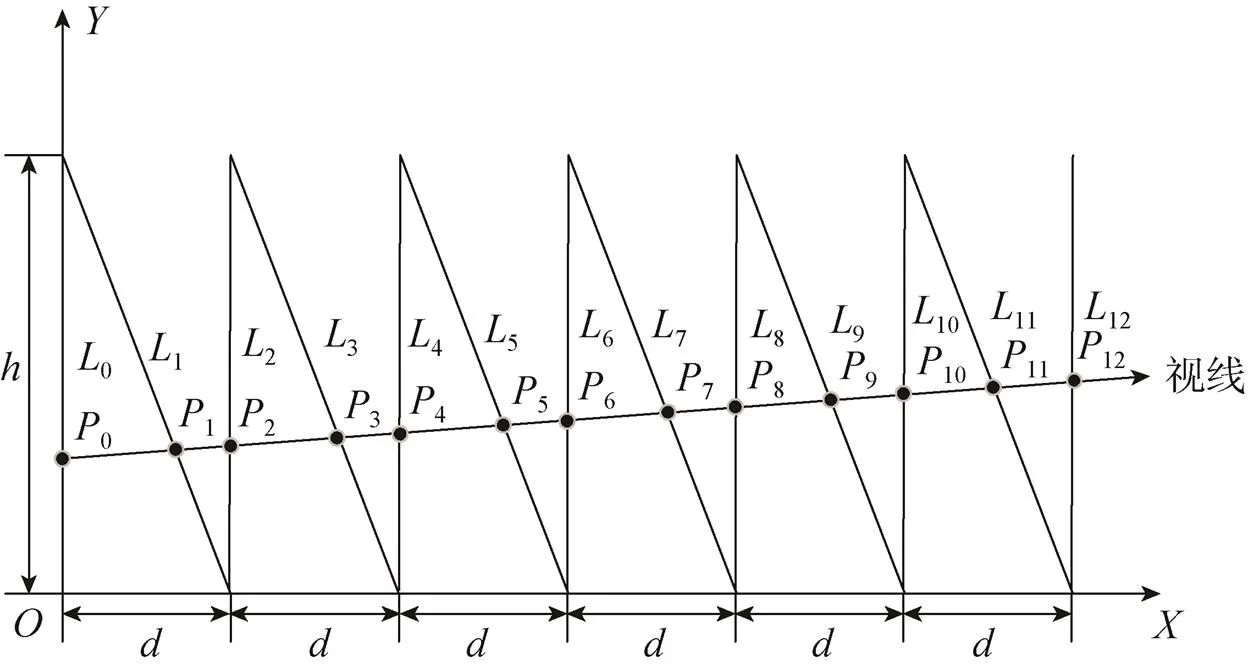
图3 标定板
2.2 采集图像
将线扫描相机、光源以及标定板固定好,使线扫描相机对准标定板,对标定板进行拍照,由于相机是静止不动的,所以可以在相机视线上得到一维数据,视线与标定板图样的线条相交有13个点(特征点),因此在线扫描相机像面上得到这13个点的一维信息,并且可以推算各个特征点的位置信息。图4为标定板成像图。
视线与标定板图样的交点为0,1,2,···,12,同一视线拍数幅图,可以拼接成一幅图,但依旧是一维信息,在这幅图像上获得与0,1,2,···,12相对应的像点0,1,2,···,12,如图4中13条黑竖线,并且可以得到
式中为正整数。
结合式(1),由此可以得到标定点的横坐标与纵坐标,对于1,3,5,…,2n-1特征点,其横纵坐标分别为
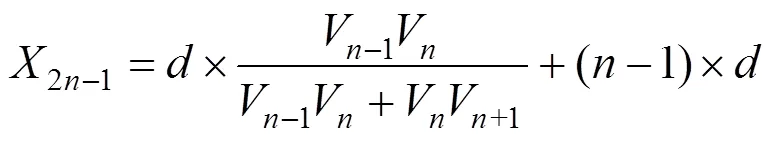
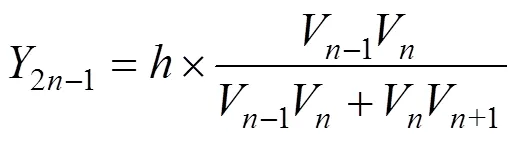
同理,可以计算2,4,6,…,2n的横纵坐标,分别为

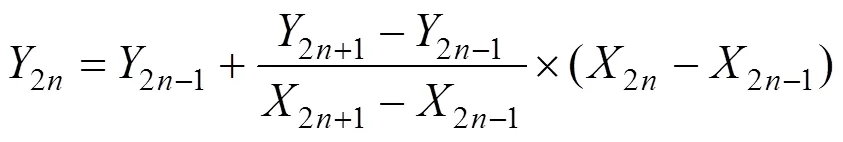
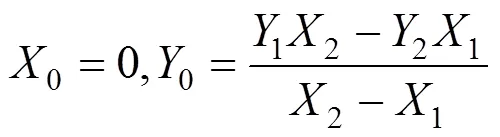
2.3 创建二维图像数据
得到标定板的特征点和它们在图像坐标系下的相关位置后,开始相机标定。文献[12]和文献[13]提出的标定方法都是针对面阵相机,在这种情况下,本文提出了一种新方法,即创建一组数据既适用于面阵相机标定,并且不会改变线扫描相机获得的信息。
用线扫描相机对静止物体进行拍照,只能获得水平方向上的有效数据,此水平方向的数据为线扫描相机探测器获得的一维数据,而垂直方向的数据只是时间累积的结果,即重复水平方向的一维数据。虽然采集图像时可以得到特征点的二维位置信息,但是这些特征点都位于同一视线上,也就是说,这些来自物方的特征点都是线性相关的。然而,当前基于面阵探测器相机的标定方法无法接受线性相关的输入数据。因此,将一维数据变为二维数据并且线性独立,同时与线扫描相机标定的结果保持一致。本文提出的解决方案是创建一个二维图像坐标,即在垂直维度上添加另一组与原始一维数据完全相同的图像数据。这意味着在水平方向上存在的透镜畸变将对垂直方向施加相同的效果。
根据镜头畸变的相关原理[14],径向畸变是像点沿径向方向移动,其数学模型为
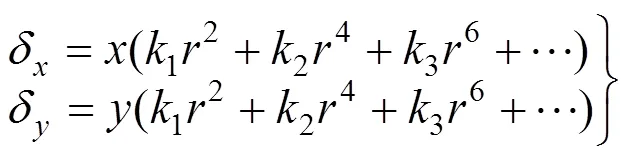
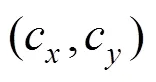
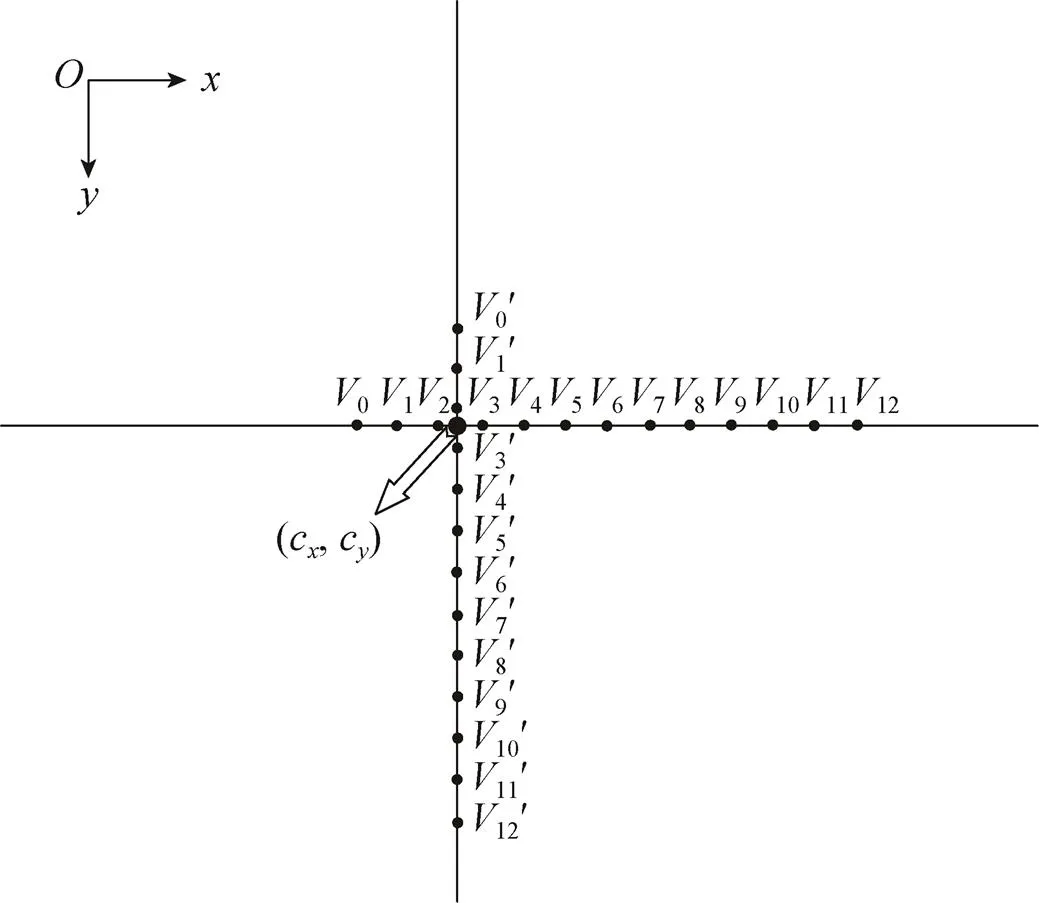
图5 二维图像数据的创建
2.4 参数计算
考虑到平面的单应性[16],即二维平面上的点映射到相机的成像平面上,那么,三维点到像面上的点的映射可以用矩阵相乘的方式表示,且点与点空间位置关系如图6所示,图6描述了世界坐标系、相机坐标系、成像平面坐标系与图像坐标系之间的关系[17-19],三维点到二维像点的数学表达式可以表述为
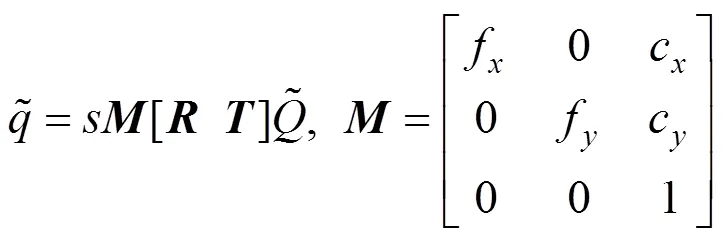
式中 Q是世界坐标系中的一点,;q是像面坐标系的一点,;s是一个任意尺度比列;是外部参数,表示旋转矩阵和平移矩阵;M是内部参数;是主点坐标;分别对应在u轴和v轴上的焦距。
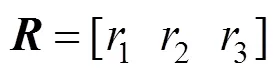
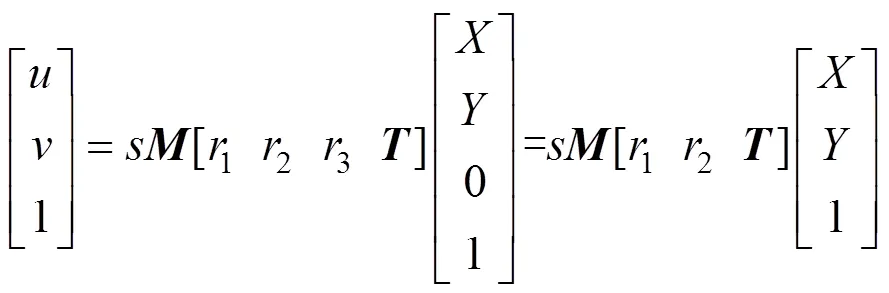
根据式(9),不难得到关于像点与物点的关系[20]。
而旋转向量在构造中是相互正交的,即
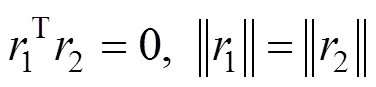
参考文献[12]提出的最大似然估计方法,给出关于标定板平面的幅图像和个特征点,并考虑到采集的图像像点因镜头畸变和噪音而失真,那么,可以通过最小化下面的函数得到最大似然估计

3 畸变矫正
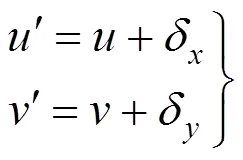
对于线扫描相机,方向的畸变量可以忽略,因此,由式(7)和式(12)可以得到
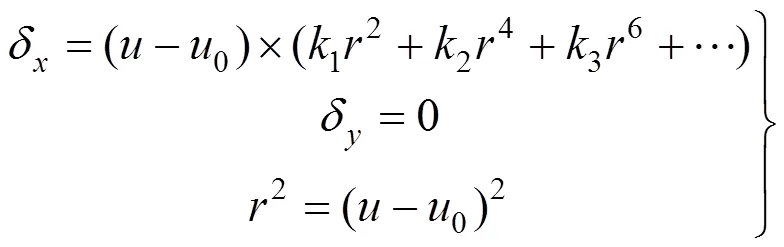
通过计算,可以得到矫正后的点
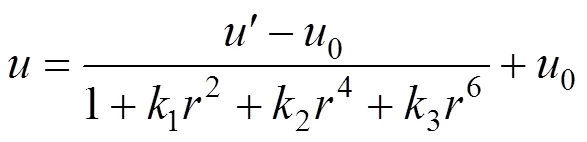
由于计算的非失真点并不是整数像素点,使用KR插值算法[22]获得均匀分布的亚像素点灰度信息,然后应用1/10细分技术来选出图像点,最后将这些点拟合到所需的未失真图像坐标。
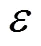
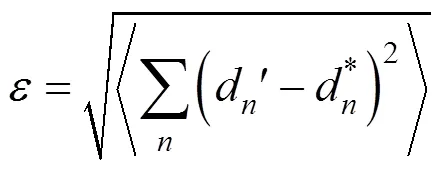
通过上述的相机标定方法,用本光学系统对标定板进行拍摄,计算相机各个参数,得出=26mm线扫描相机的标定结果,见表1。
表1 相机参数

Tab.1 Camera parameters
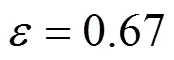
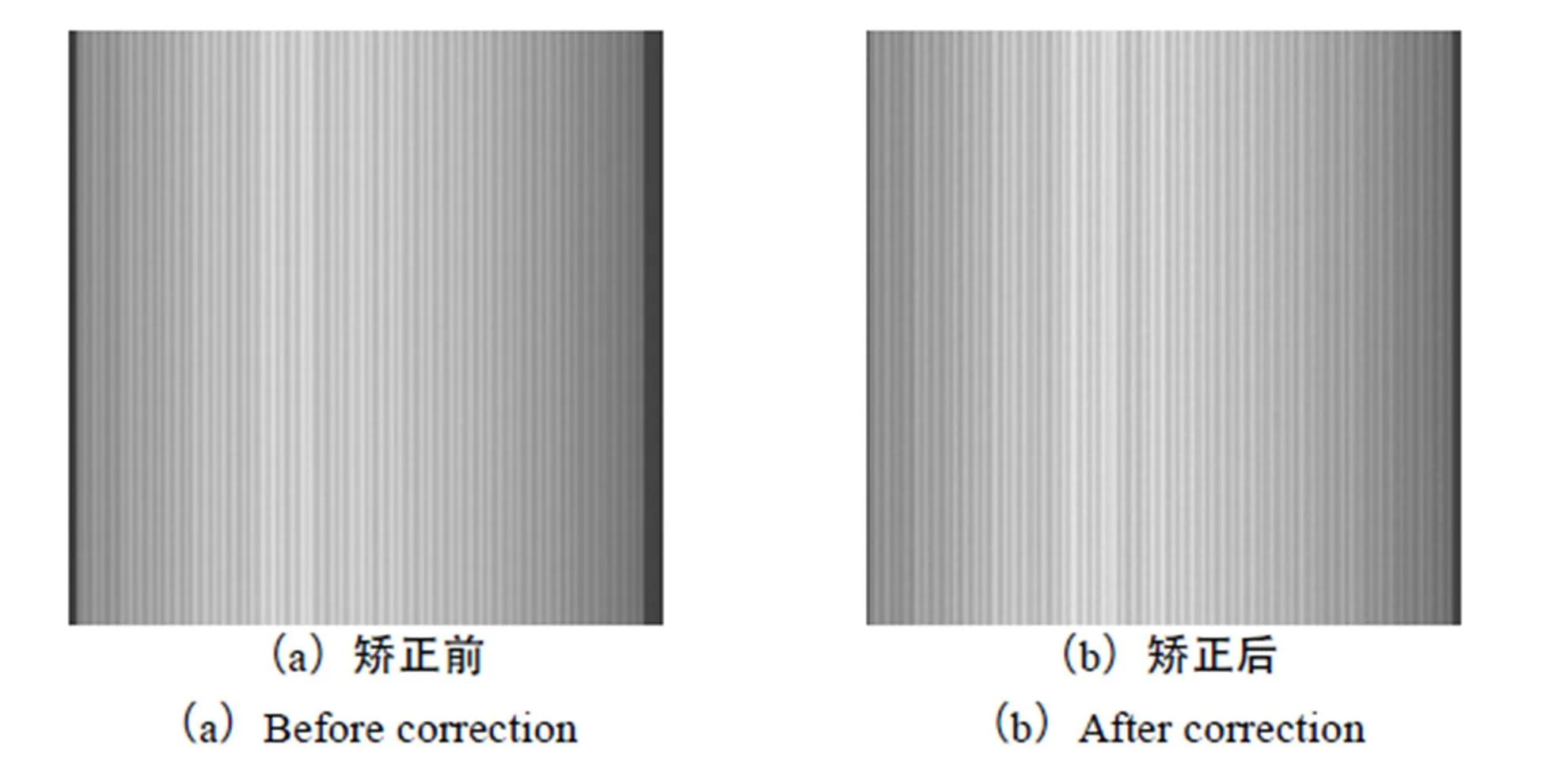
图7 畸变矫正结果
为了验证畸变矫正算法的准确性,对5幅标定板试验参与的情况下进行畸变矫正,试验图像的畸变矫正结果如表2所示,从表2中可以看出,畸变平均矫正精度优于1个像素。
表2 畸变矫正精度

Tab.2 The accuracy of distortion correction
4 结束语
本文对线扫描相机的原理进行了简单的介绍,详细阐述了如何将线扫描相机采集的一维数据映射成二维图像数据以适用于现有的面阵相机的标定方法。在制备新型标定板的情况下,建立世界坐标系和图像坐标系之间的关系,以求解相机的内外参数以及畸变系数。而对于线扫描相机的畸变,只需要矫正水平方向即可。该相机标定以及畸变矫正方法操作简单,标定板制备容易,并且能够实现较好的畸变矫正效果,畸变平均矫正精度均优于1个像素。
[1] LUNA C A, MAZO M, LÁZARO J L, et al. Calibration of Line-scan Cameras[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(8): 2185-2190.
[2] KATAOKA K, OSAWA T, OZAWA S, et al. 3D Building Façade Model Reconstruction Using Parallel Images Acquired by Line Scan Cameras[C]//IEEE International Conference on Image Processing, Genova, 2005, 1: I-1009.
[3] LI Y S, YOUNG T Y, MAGERL J A. Subpixel Edge Detection and Estimation with A Microprocessor- controlled Line Scan Camera [J]. IEEE Transactions on Industrial Electronics, 1988, 35(1): 105-112.
[4] DOUXCHAMPS D, MACQ B, CHIHARA K. High Accuracy Traffic Monitoring Using Road-Side Line-Scan Cameras[C]// IEEE Intelligent Transportation Systems Conference, Toronto, 2006: 875-878.
[5] CHRISTENSEN H I, FÖRSTNER W. Editorial Performance Characteristics of Vision Algorithms[J]. Machine Vision & Applications, 1997, 9(5): 215-218.
[6] FANG S, XIA X, XIAO Y. A Calibration Method of Lens Distortion for Line Scan Cameras[J]. Optik-international Journal for Light and Electron Optics, 2013, 124(24): 6749-6751.
[7] 李晋惠, 韩黄璞. CCD 光学系统成像畸变量与视场角的标定[J]. 西安工业大学学报, 2012, 32(2): 99-102. LI Jinhui, HAN Huangpu. Calibrating Aberrations and Visual Angles in the CCD Imaging Optical System[J]. Journal of Xi’an Technological University, 2012, 32(2): 99-102. (in Chinese)
[8] WENG J, COHEN P, HERNIOU M. Camera Calibration with Distortion Models and Accuracy Evaluation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(10): 965-980.
[9] PERŠ J, KOVACIC S. Nonparametric, Model-based Radial Lens Distortion Correction Using Tilted Camera Assumption[C]// Proceedings of the Computer Vision Winter Workshop, 2002, 1: 286-295.
[10] PRESCOTT B, MCLEAN G F. Line-based Correction of Radial Lens Distortion[J]. Graphical Models and Image Processing, 1997, 59(1): 39-47.
[11] 罗红娥, 陈平, 顾金良, 等. 线阵 CCD 测量系统的镜头畸变校正新方法[J]. 半导体光电, 2009, 30(3): 441-443. LUO Honge, CHEN Ping, GU Jinliang, et al. A New Method of Lens Distortion Calibration of Linear CCD Measurement System[J]. Semiconductor Optoelectronics, 2009, 30(3): 441-443. (in Chinese)
[12] ZHANG Z. Camera Calibration with One-dimensional Objects[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(7): 892-899.
[13] LIU H, YANG L, GUO Y, et al. Precise Calibration of Linear Camera Equipped with Cylindrical Lenses Using a Radial Basis Function-based Mapping Technique[J]. Optics Express, 2015, 23(3): 3412-3426.
[14] 刘金国. 大视场光电测量系统的精密几何标定和畸变校正的研究[J]. 光学精密工程, 1994, 2(4): 109-120. LIU Jinguo. Study on High Accurate Geometric Calibration of Precision Photo-electronic Measuring System with Large Field of View and Distortion Correcting[J]. Optics and Precision Engineering, 1994, 2(4): 109-120. (in Chinese)
[15] 张蔚, 李恩普, 陈建明. 大视场光学系统畸变曲线拟合[J]. 电光与控制, 2004, 11(4): 57-59. ZHANG Wei, LI Enpu, CHEN Jianming. Curved-fitting Methods for Distortion Correction of Large-FOV Optical System[J]. Electronics Optics & Control, 2004, 11(4): 57-59. (in Chinese)
[16] ZHANG Z. A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.
[17] TSAI R. A Versatile Camera Calibration Technique for High-accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses[J]. IEEE Journal on Robotics and Automation, 1987, 3(4): 323-344.
[18] LIU Y, HUANG T S, FAUGERAS O D. Determination of Camera Location from 2-D to 3-D Line and Point Correspondences[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(1): 28-37.
[19] HEIKKILA J, SILVEN O. A Four-step Camera Calibration Procedure with Implicit Image Correction [C]//Computer Vision and Pattern Recognition, 1997 Proceedings, 1997 IEEE Computer Society Conference on. IEEE, 1997: 1106-1112.
[20] 李立春, 许颖慧, 孟彦鹏, 等. 月面探测中的单目相机成像测量方法[J]. 航天返回与遥感, 2015, 36(5): 36-43. LI Lichun, XU Yinghui, MENG Yanpeng, et al. Measurement Method Based on Image of Mono-view in Lunar Exploration[J]. Spacecraft Recovery and Remote Sensing, 2015, 36(5): 36-43. (in Chinese)
[21] MORÉ J J. The Levenberg-marquardt Algorithm: Implementation and Theory[M]//Numerical Analysis. Berlin: Springer Berlin Heidelberg, 1978: 105-116.
[22] TAKEDA H, FARSIU S, MILANFAR P. Kernel Regression for Image Processing and Reconstruction[J]. IEEE Transactions on Image Processing, 2007, 16(2): 349-366.
(编辑:王丽霞)
Calibration and Distortion Correction Method of Line Scan Camera
ZHU Yao WANG Zhile HE Lei ZHOU Chenghao
(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)
Line scan cameras are more and more widely used in measurement filed owning to their high resolution and high data-processing efficiency. However, optical distortion of the line scan camera can have direct impact on the accuracy of geometric position, and even results in a failure to image. In this paper, a method mapping data from one dimension to two dimension without changing the original ones is proposed to calibrate the line scan camera using the existing area-based calibration method. During the calibration, a new calibration pattern is used to correlate the world coordinate system and the image coordinate system. The digital image processing method is used to calibrate and correct the distortion of the optical lens, which basically eliminates the measurement error caused by the image deformation and effectively solves the problem of reducing the accuracy of geometric position due to the lens distortion.
image processing; camera calibration; distortion correction; line scan camera
V557+.1
A
1009-8518(2017)06-0046-08
10.3969/j.issn.1009-8518.2017.06.006
朱瑶,男,1991年生,2016年获哈尔滨工业大学光学工程专业工程硕士学位,现在哈尔滨工业大学光学工程专业攻读博士学位。研究方向为光学图像处理技术和光电系统半实物仿真技术。E-mail:yuzhimingren@163.com。
2017-04-12
国家重大科学仪器设备开发专项(2013YQ350747)

