星载红外点目标探测系统瞬时视场优化模型

童锡良周峰



星载红外点目标探测系统瞬时视场优化模型

童锡良1,2周峰1

（1 北京空间机电研究所，北京 100094）（2 先进光学遥感技术北京市重点实验室，北京 100094）

瞬时视场是影响星载红外点目标探测系统性能的重要指标，为了实现高信噪比探测，有限口径的空间相机设计需要选择合适的瞬时视场。文章讨论了衍射受限条件下，瞬时视场对能量集中度、采样相位因子、背景杂波和信噪比的影响，建立了以信噪比最大化为目标函数的瞬时视场优化模型。基于在轨遥感图像统计背景杂波，确定了杂波系数范围和不同杂波程度的背景分布。结合实例仿真，计算了不同瞬时视场下的信号响应和信噪比变化，通过分析得出结论：随着瞬时视场减小，点目标能量集中度降低，采样相位影响减小，探测稳定性提高，杂波减小，信噪比先增大后减小，利用优化模型能得到最优瞬时视场。文章提出的模型可用于空间相机的指标设计和优化。

瞬时视场 采样相位因子 能量集中度 红外波段 点目标探测 空间相机

0 引言

星载红外预警相机利用目标和背景的红外辐射差异，对主动段导弹尾焰进行探测。导弹预警探测距离远，背景杂波干扰强，探测器接收到的目标信号较弱，导弹及尾焰在像面的成像面积小于一个像元，因此预警相机是复杂背景下的动弱点目标探测系统[1-2]。要实现对广域范围内快速、稳定、可靠的预警探测，要求点目标探测系统具有大视场、短重访周期、高探测率和低虚警率的特点[3-4]。

瞬时视场决定了相机在观测视场内一定探测距离处的空间分辨能力，从多方面影响系统整体性能。选择小瞬时视场时，目标所在像元混合的背景能量少，目标背景对比度更高；背景辐射响应下降，杂波减小，信噪比提高；在准确探测的基础上还能提高定位精度。但随着瞬时视场减小，要实现大范围覆盖，需要更大的焦平面探测器规模，这些对探测器响应非均匀性、读出电路都提出了更高的要求，增加了后续处理和传输的数据量。因此，瞬时视场不是单一孤立的技术指标，瞬时视场分析对相机性能和优化模型的影响具有重要意义。

琼斯准则对目标的探测、识别、确认等的不同层次，提出了不同的最低分辨率要求，即目标尺度内的最少线对数[5]。但点目标成像为小弥散斑，其分布特征和检测方法有别于传统面源目标，因此琼斯准则的应用有一定局限性。文献[6]提出星载点目标探测系统一般采用小像元尺寸，可通过调节有效焦距来改变地面像元分辨率，在满足复杂背景下探测性能需求同时尽可能采用较大的地面分辨率；文献[7]针对分辨空间相关帧间邻近点源提出了基于统计学的角分辨率限，可用作目标定位性能标准。对于星载点目标探测系统，应该结合性能要求、探测场景、点目标成像特征、信噪比和检测模型等对瞬时视场进行综合优化。本文针对TDI扫描探测相机，分析了瞬时视场对能量集中度、采样相位因子、噪声和信噪比的影响机制，建立了信噪比最大化的瞬时视场优化模型，并结合实例参数进行计算。

1 点目标探测原理

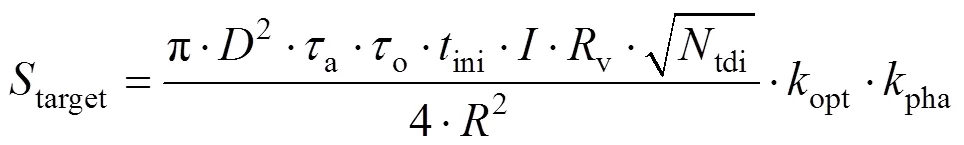
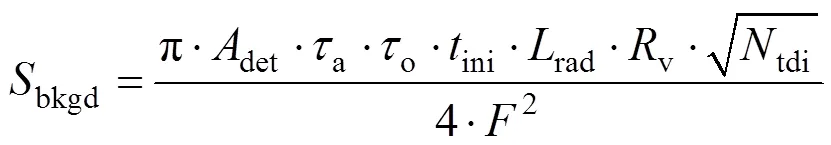
1.1 能量集中度

受光学系统像差和衍射的影响，点源目标实际成像为一个弥散斑，像斑尺度为3~5个像元大小。能量集中度指目标主像元收集的能量与目标到达焦面总能量的百分比，取值范围在0到1之间。在设计点目标探测系统时，一般要使大部分的目标能量集中在某一个像元上，即实现高能量集中度[12-14]。提高光学系统设计水平可减小几何像差，使性能接近衍射极限，此时光学系统点扩散函数的主要影响因素是衍射效应，衍射受限于孔径光阑。依据夫朗和费远场衍射模型，衍射强度分布为[15]

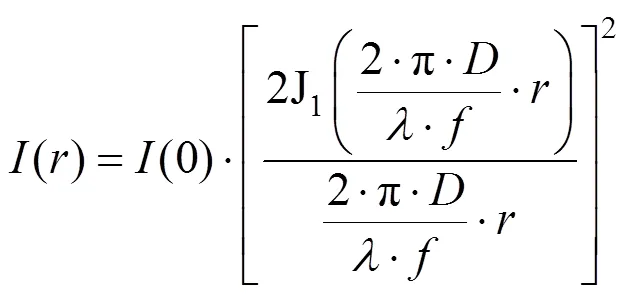
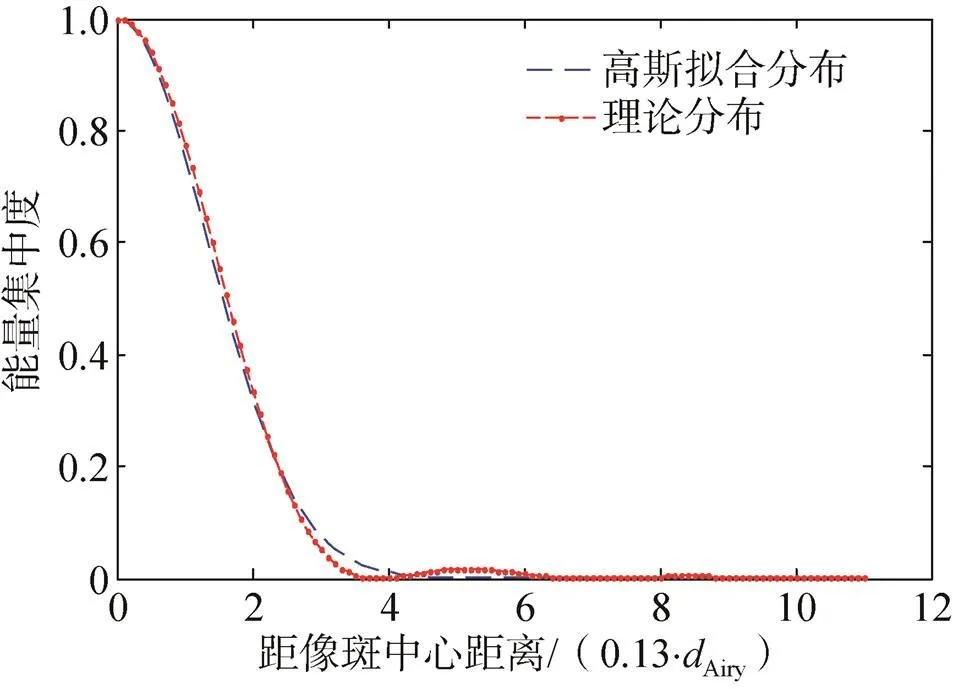
图1 像斑强度理论分布和高斯拟合分布

假设光强分布随径向距离变化的高斯模型（）为

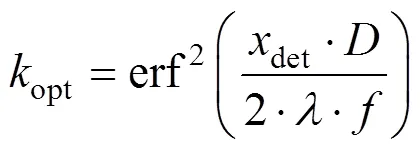
1.2 采样相位因子

TDI扫描系统对点目标的采样相位等于目标中心相对像元中心的位移与像元尺寸之比。采样相位因子是指采样相位导致能量集中度下降的影响因子。TDI扫描系统需要电荷转移的速度与CCD像平面上的图像转移速度完全保持一致，否则会导致扫描方向上的图像模糊和几何变形[17]。假设在TDICCD扫描方向上存在非正常像移时，第一级扫过的面积大于一个像元尺寸，则从第二级开始，其积分的初始位置便不再与第一级的积分初始位置重合，随着积分级数的增加，这种错位便会越来越严重，即成像点扩散函数的中心位置偏离越大，当多级采样叠加后，便会造成点目标像斑半径增大和像斑中心 偏移。

除TDICCD行转移速度和相移匹配误差之外，速高比变化、卫星姿态稳定度、偏流角、平台颤振等因素也会导致扫描方向和线列方向的相对位移，最终延时积分结果是一个有模糊和采样相位的像斑[18]。

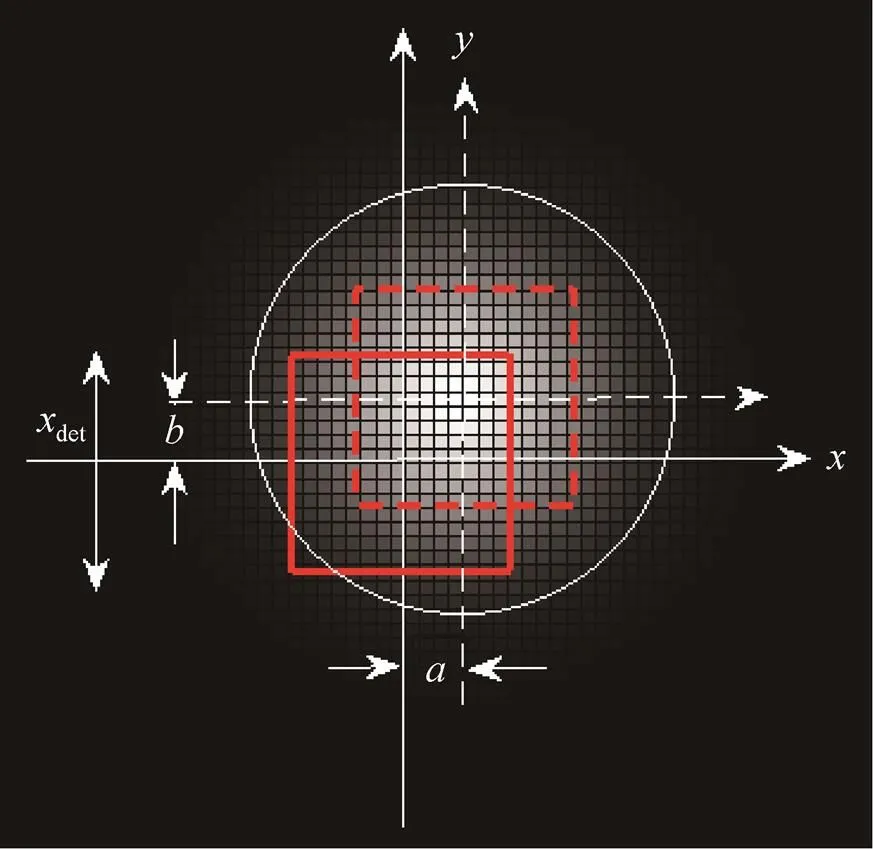
图2 有相位差时的采样示意图

当像元中心恰好与积分像斑中心重合时，目标主像元收集的能量最多，能量集中度最大[18]。但大部分情况下，像元中心距离像斑中心有一定位移，采样情况见图2。白色弥散斑表示点目标在像面所成的像，红色方框表示探测像元，像元尺寸为。坐标轴分别表示探测器线列向和采样方向，两者互相垂直；，表示两个方向上的相移，和的取值范围是。

1.3 信噪比和噪声模型

杂波是指背景中与点目标特征类似，会影响目标检测的信号，在图像上一般表现为突变的边缘、尖峰或其他目标疑似物，一般采取合适的杂波量化尺度进行估计。光子噪声是由入射辐射的量子特性引起的，表现入射光的涨落特性，造成光子噪声的光子数是目标背景总光子数的均方根。以上两种噪声是与入射辐射相关的噪声。暗电流和读出电路噪声由器件和电路设计水平决定，在选用特定器件和电路设计下，这两种噪声一般比较稳定。

2 瞬时视场优化模型

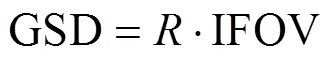
在焦距一定的情况下，像元尺寸越小，空间分辨率越高，但像元尺寸减小会使光敏面积减小，导致系统灵敏度下降；此外，像元尺寸受限于技术成熟度和工艺水平。因此，一般选定探测器确定像元尺寸后，通过调节系统焦距调节瞬时视场。下面讨论瞬时视场变化对能量集中度、相位衰减因子和噪声的影响，并以信噪比为目标函数建立瞬时视场优化模型。

2.1 对能量集中度的影响

由式（7）和式（12）可到能量集中度与瞬时视场的关系为

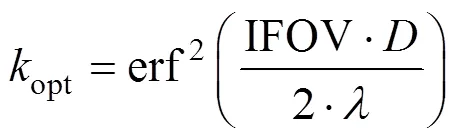
设计光学系统初始参数，使艾里斑直径恰好等于探测像元尺寸，此时能量集中度等于0.838。假设初始设计下，焦距等于0，对应的瞬时视场为IFOV0，在此基础上改变焦距来调节瞬时视场，得到能量集中度计算结果见表1，瞬时视场和能量集中度随焦距的变化曲线见图3。由计算结果可知随着瞬时视场减小，点目标能量集中度降低。

表1 不同瞬时视场下的能量集中度

Tab.1 Energy concentration at different IFOV

2.2 对相位衰减的影响

改变瞬时视场会对相位衰减产生两方面影响。首先，小瞬时视场意味着对场景采样更密集，在相同的随机中心距下，对点源目标以更小分辨率进行滑动积分，相位变化更大，尤其在TDI多级积分时，相位变化剧烈，叠加得到的点扩散函数更平滑。其次改变瞬时视场会使衍射像斑大小变化，通过增大焦距减小瞬时视场，艾里斑直径会增大，弥散加剧。

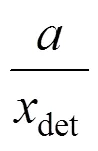
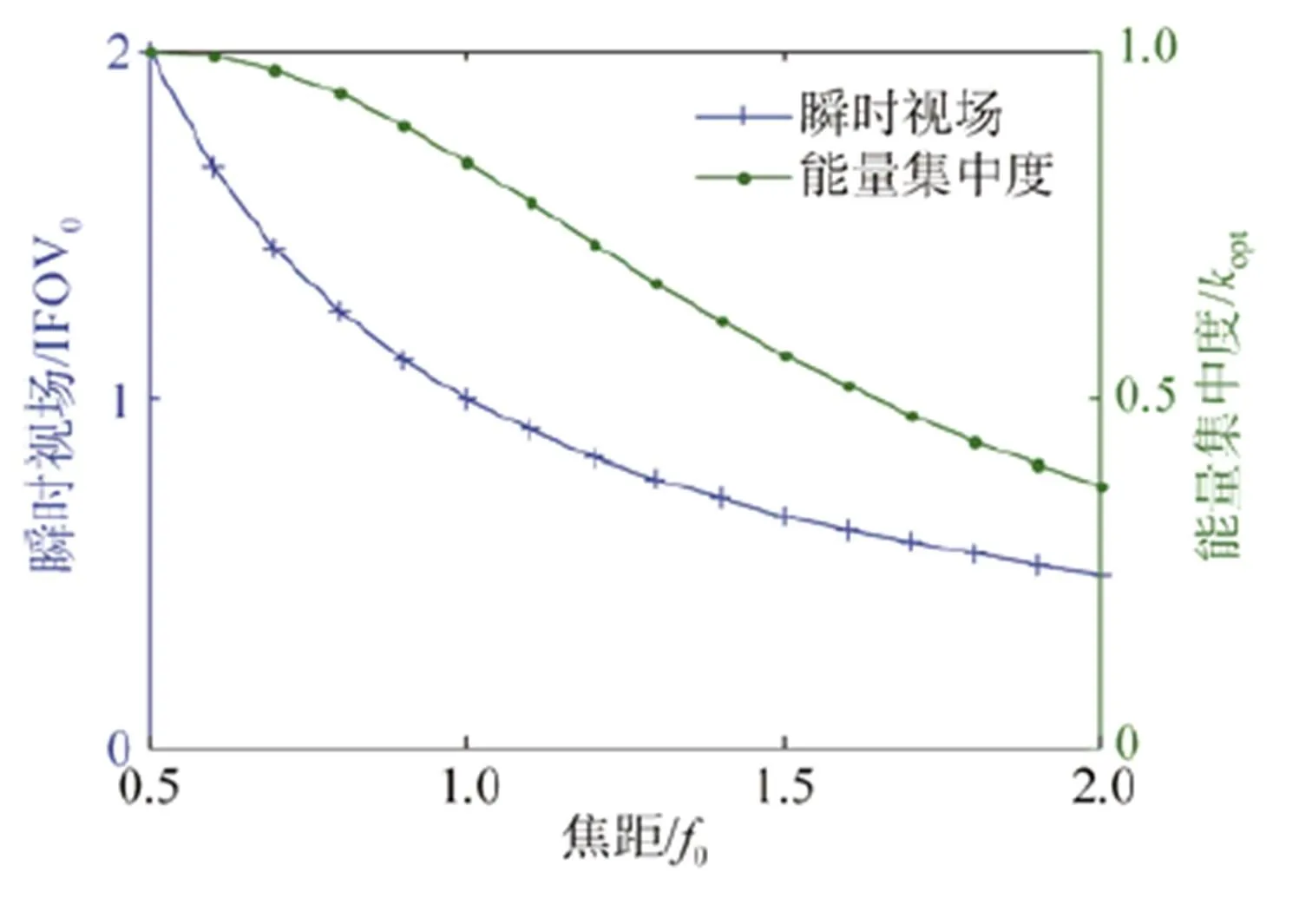
图3 瞬时视场和能量集中度随焦距调节系数的变化

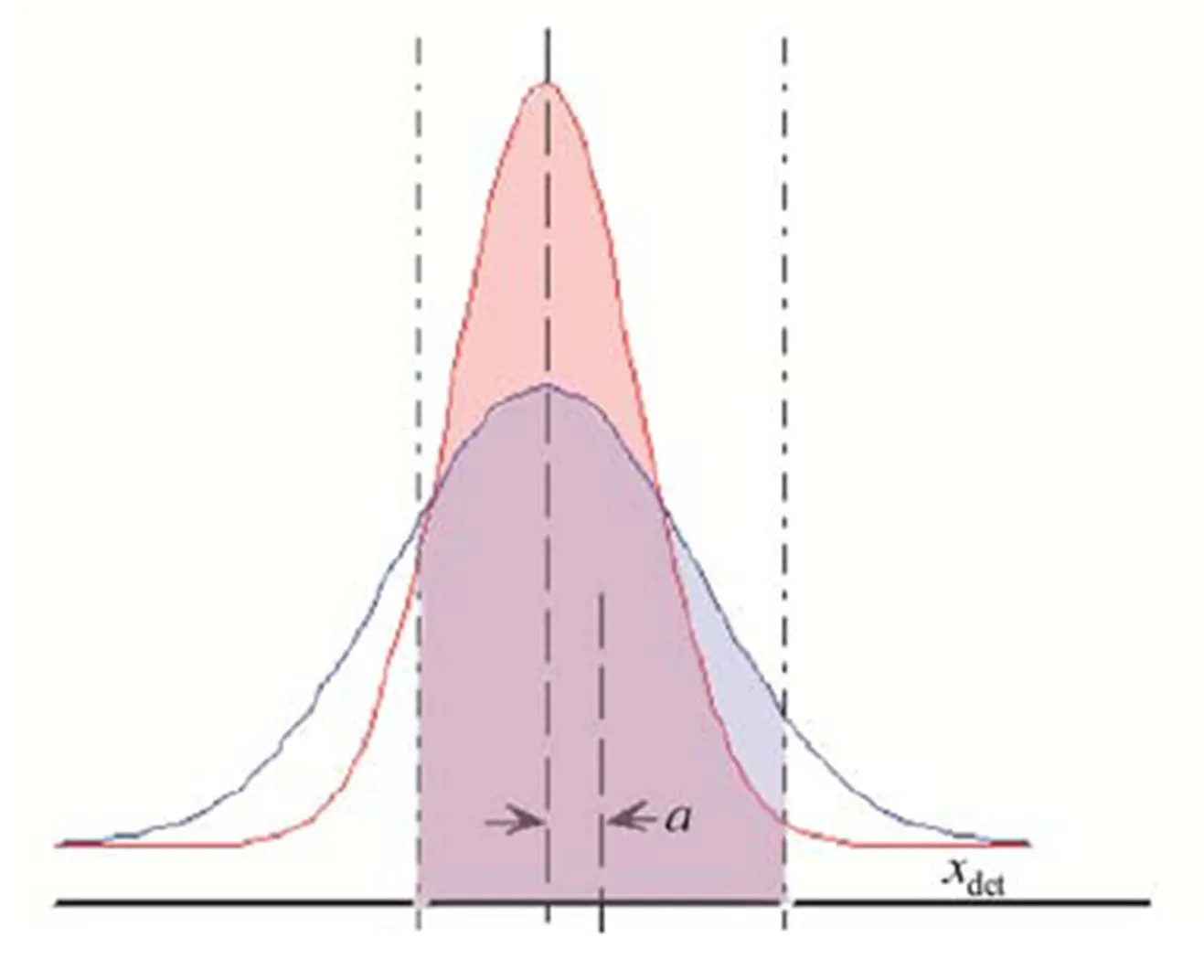
图4 不同弥散程度下的一维采样示意图

一维采样相位衰减因子定义为

减小瞬时视场，像斑弥散加剧。计算不同弥散像斑的相位衰减因子见表2，其中弥散因子越大表示像斑弥散越严重，能量更分散。对于同一采样相位，随着弥散加剧，相位衰减因子不断减小。通过比较不同弥散像斑的集中度衰减因子对采样相位的变化情况，可发现能量集中像斑的相位衰减因子随相位增加衰减更快。

表2 不同条件下的相位衰减因子

Tab.2 Phase attenuation factors at different phase and dispersion factors

2.3 对噪声的影响

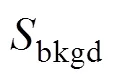
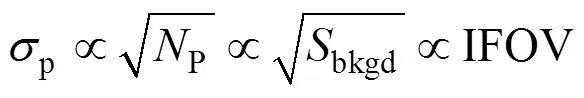
背景杂波若采用目标尺度相关的背景标准差为度量，则正比于背景信号，针对某一特定空间结构的背景，用杂波系数描述杂波程度，杂波、背景响应和瞬时视场之间存在以下关系

2.4 瞬时视场优化模型

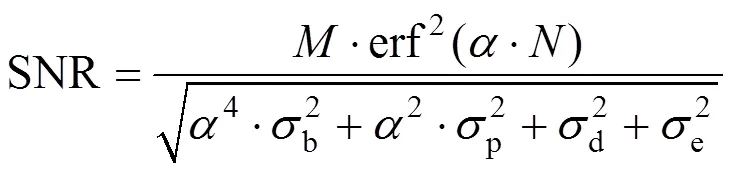
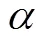
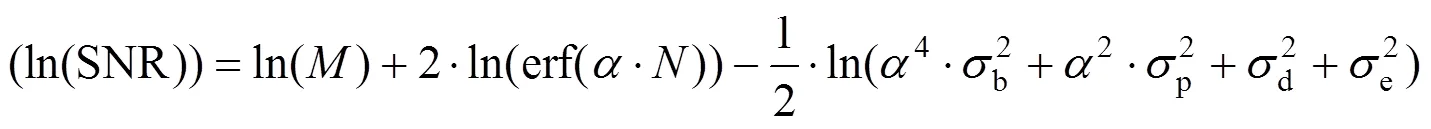
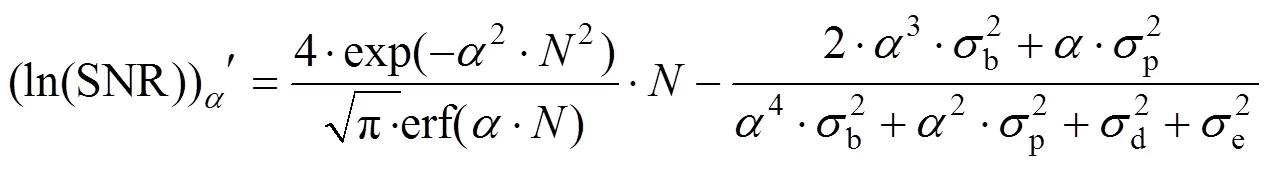
综合2.1~2.4节分析，瞬时视场对信噪比有以下影响规律：

1）由式（13）可知，当瞬时视场很小时，目标能量集中度低，信噪比小；随着瞬时视场增大，点目标能量集中度按照误差函数的平方速率增长；

2）由式（16）和式（17）可知，随着瞬时视场增大，辐射相关噪声增加，辐射无关噪声保持不变，信噪比随之增大；

3）由式（18）可知，随着瞬时视场增大，目标信号和噪声都增大；当目标能量集中度趋于稳定后，目标信号不再增加，而辐射相关噪声继续增大，信噪比降低。

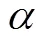
3 实例计算仿真与分析

以地球同步静止轨道上的红外点目标探测场景为例，仿真瞬时视场对信噪比的影响及优化过程，探测距离为35 786km，探测谱段为短波红外（2.7μm~2.95μm）。由大气辐射模型计算软件Modtran计算，在美国1976年标准大气模式下，观测天顶角在0°~10°，太阳高度角20°~90°，地面背景光谱辐亮度平均为3.0μW·cm–2·sr–1μm–1，假设目标在探测谱段的辐射强度为5×104W/sr，大气透过率为0.7，系统初始设计参数见表3。

表3 光学系统、探测器及电子系统参数

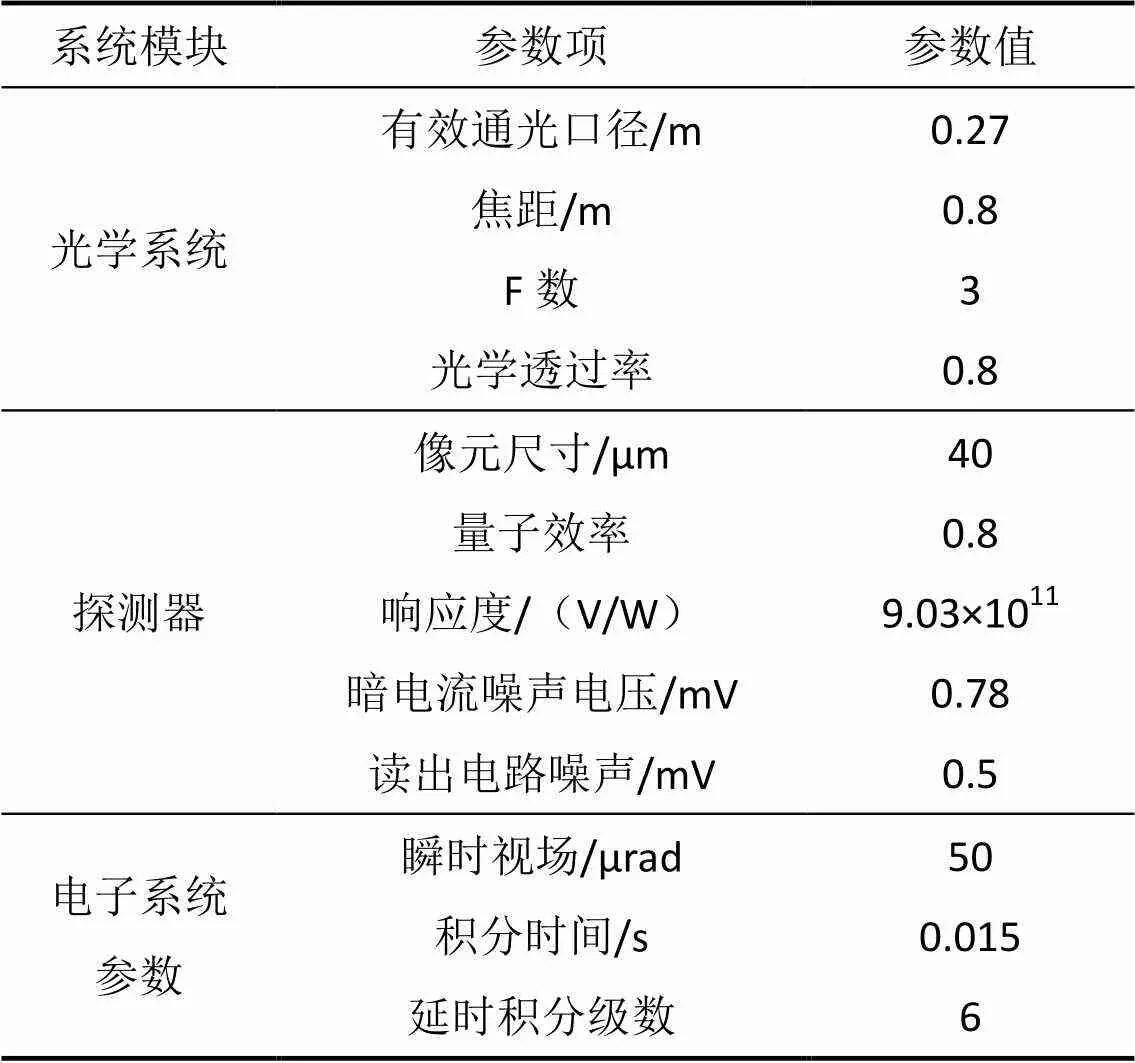
Tab.3 Properties of optical system, detector and electric system

背景杂波随背景结构和辐射强度变化而变化。由不同地理边界、云层边缘等高频信息造成不同杂波程度的背景见图5。为了选取合适的杂波系数，利用在轨红外图像分析地面背景杂波。采用局部方差统计法，以11像元×11像元作为子单元大小，对600多帧在轨红外图像进行杂波统计，结果见图6，杂波系数分布在0~0.1之间。图6（a）中按杂波系数从小到大进行帧序数排列，图6（b）统计了不同杂波系数对应的图像累计帧数。为了满足复杂背景强杂波系数条件下的探测性能要求，取杂波系数为0.1。

图5 不同程度杂波的背景

图6 杂波系数累积统计样本随杂波程度的分布

利用表3参数计算出信噪比为23。保持其他参数不变，通过改变焦距来调整瞬时视场，计算不同瞬时视场下的目标响应、各噪声分量及信噪比，结果见表4。

表4 不同瞬时视场下的信噪比计算结果

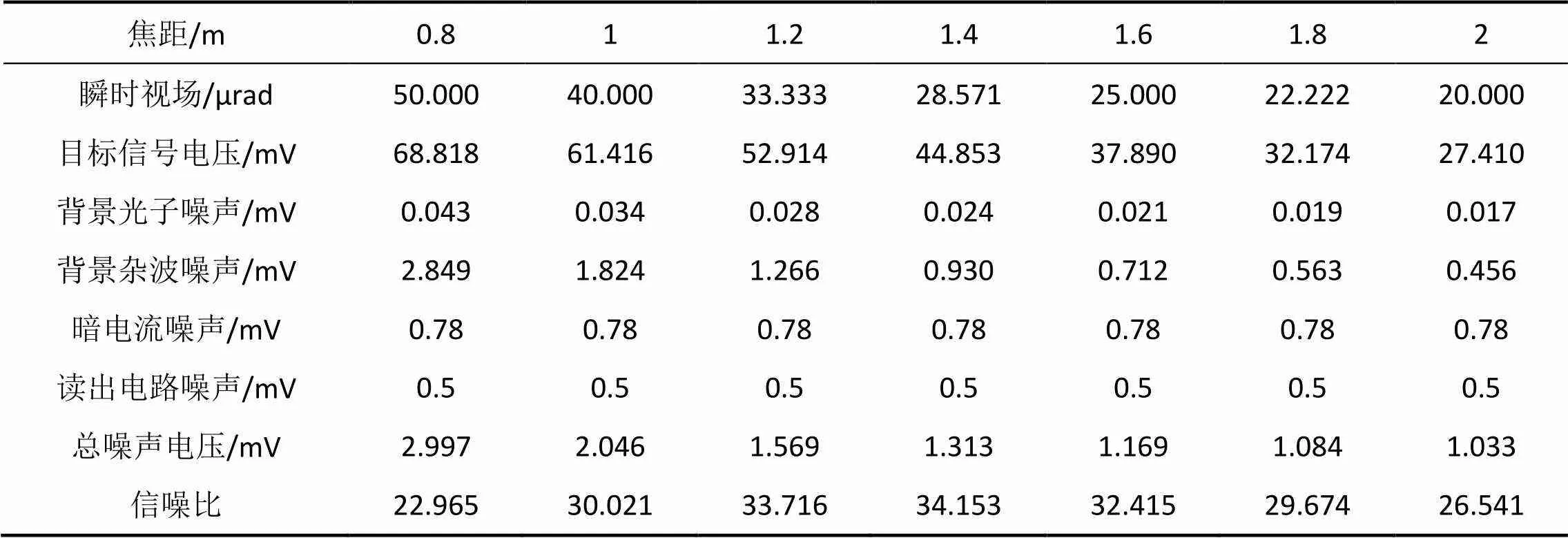
Tab.4 Intermediate results and SNR at different IFOV

目标响应电压、噪声电压和信噪比随瞬时视场的变化曲线见图7，随着瞬时视场增大，目标响应电压增大，但增加速度减缓，最终趋于理想点目标响应。随着瞬时视场增大，噪声增加且增速加快，最终呈线性增涨，其中杂波占比逐渐增大，成为主要噪声成分。基于目标信号和噪声随瞬时视场的变化规律，计算得到信噪比随瞬时视场调节先增大后减小。在本文仿真参数下，大约在30μrad处取得信噪比最大值，因此最优瞬时视场取30μrad。

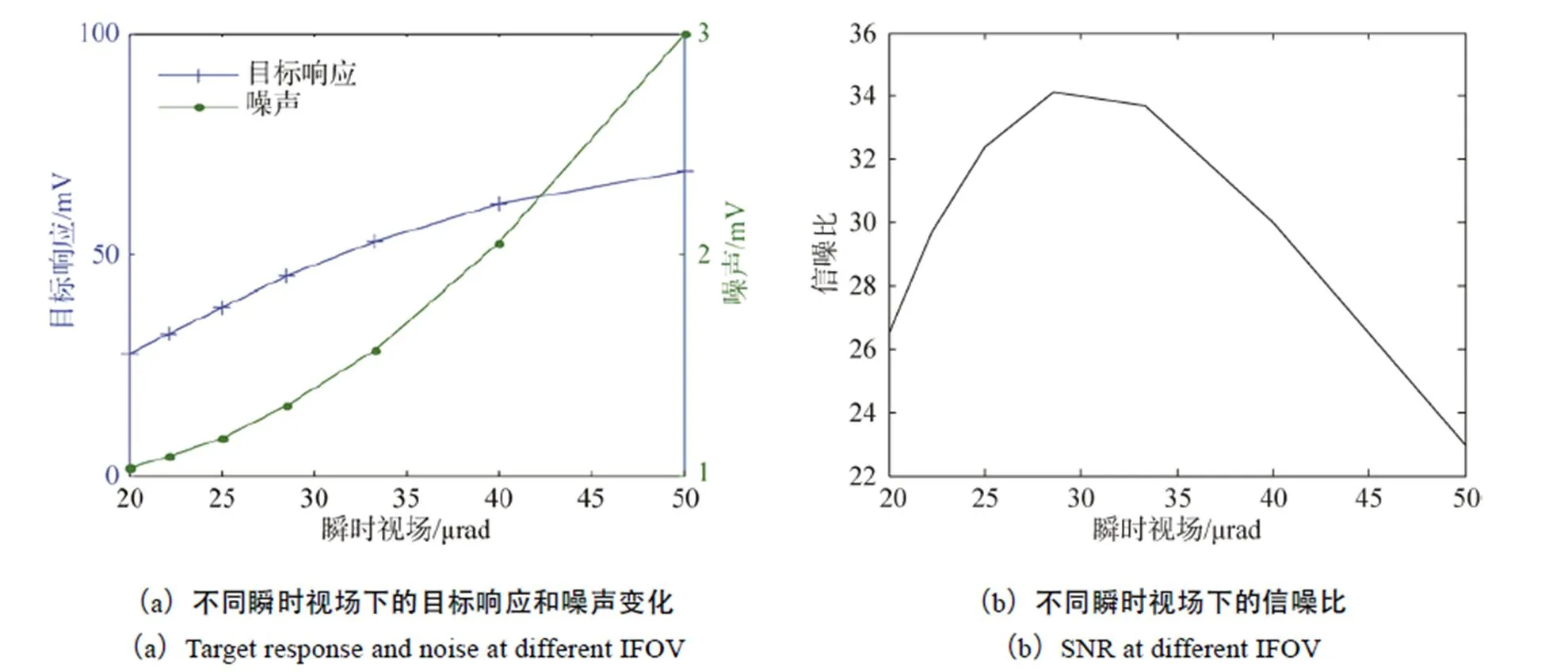
图7 点目标响应、噪声和信噪比随瞬时视场的变化

根据式（21）做出对数信噪比关于瞬时视场调节系数的导数的变化曲线，见图8。由曲线可知调节系数从0.5变化到3，对数信噪比关于的导数经历由正到负不断减小至基本不变，说明在此阶段信噪比先增大，增加趋势减缓，到达峰值后开始减小，并加速下降。当等于0.596时，导数值为0，此时信噪比最大，对应瞬时视场为29.8μrad。由解析模型法得到的最优瞬时视场和采样拟合结果基本一致，因此可直接利用解析优化模型得出最优瞬时视场。

图8 信噪比关于瞬时视场调节系数的导数的变化曲线

4 结束语

本文对衍射受限条件下点目标探测系统的瞬时视场优化问题进行了讨论，分析了瞬时视场对能量集中度、采样相位因子、噪声和信噪比的影响，得出结论：减小瞬时视场会降低目标能量集中度，减小采样相位影响，提高探测稳定性，降低背景杂波和光子噪声，分析表明在一定区间内存在最优瞬时视场使信噪比最大。提出了点目标探测系统瞬时视场优化模型，该模型基于目标背景特性和初始系统参数，求解瞬时视场调节系数，适用于部分参数确定时衍射受限点目标探测系统的二次优化。

实际点目标探测系统优化设计除了提高信噪比，还要综合考虑视场、重访时间和系统成本等因素。此外，新型过采样体制的应用也会对信噪比模型产生影响。文中只讨论了传统采样体制下，在一定光学系统口径限制条件下的瞬时视场优化，将来可考虑结合多种指标约束，建立综合指标优化模型。

[1] 张伟, 孟祥龙, 丛明煜, 等. 天基红外扫描图像点目标检测算法[J]. 红外与激光工程, 2009, 38(5): 921-925. ZHANG Wei, MENG Xianglong, CONG Mingyu, et al. Algorithm of Space Point Target Detection for IR Scan Images[J]. Infrared and Laser Engineering, 2009, 38(5): 921-925. (in Chinese)

[2] 龙亮, 王世涛, 周峰, 等. 空间红外点目标遥感探测系统在轨辐射定标[J]. 航天返回与遥感, 2012, 33(2): 73-80. LONG Liang, WANG Shitao, ZHOU Feng, et al. In-orbit Radiometric Calibration Methods for Remote Sensing System to Detect Space Infrared Point Target[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(2): 73-80. (in Chinese)

[3] 刘可辉, 王晓蕊, 张卫国. 红外点目标成像信噪比建模分析[J]. 红外与激光工程, 2014, 43(7): 2143-2147. LIU Kehui, WANG Xiaorui, ZHANG Weiguo. Modeling and Analysis on SNR of Infrared Point Target[J]. Infrared and Laser Engineering, 2014, 43(7): 2143-2147. (in Chinese)

[4] 毛艺帆, 张多林, 王路. 美国SBIRS-HEO卫星预警能力分析[J]. 红外技术, 2014, 36(6): 467-470. MAO Yifan, ZHANG Duolin, WANG Lu. Analysis on Early Warning Capability of USA’s SBIRS-HEO Satellite[J]. Infrared Technology, 2014, 36(6): 467-470. (in Chinese)

[5] 周立伟, 刘玉岩. 目标探测与识别[M]. 北京理工大学出版社, 2004: 28-33. ZHOU Liwei, LIU Yuyan. Target Detection and Recognition[M]. Beijing Institute of Technology Press, 2004: 28-33. (in Chinese)

[6] Lomheim T S, Milne E L, Kwok J D. A Performance/Sizing Relationships for a Short-wave/Mid-wave Infrared Scanning Point-source Detection Space Sensor[C]// 1999 IEEE Aerospace Conference, Proceedings, Colorado: IEEE, 2002: 113-138.

[7] LIU Z, NehOrai A. Statistical Angular Resolution Limit for Point Sources[J]. IEEE Transactions on Signal Processing, 2007, 55(11): 5521-5527.

[8] Lawrie D G. Electro-Optical Sensor Simulation for Theatre Warning[C]// The AGARD Mission Systems Panel 5th Symposium on Space Systems as Contributors to the NATO Defense Mission, Cannes, France, 1996.

[9] 骆守俊, 李江勇, 夏寅辉, 等. 远程运动点目标探测影响因素分析[J]. 激光与红外, 2014, 44(8): 898-901.Luo Shoujun, LI Jiangyong, XIA Yinhui, et al. Influence Factors on Detection of Long Range Moving Point Target[J]. Laser & Infrared, 2014, 44(8): 898-901. (in Chinese)

[10] 董二伟, 黄旻, 李立英. 空间探测相机的能量计算[J]. 光子学报, 2009, 38(9): 2359-2362. DONG Erwei, HUANG Min, LI Liying. Energy of Space Target Detection of the Visible Camera Based on the Satellite[J]. Acta Photonica Sinica, 2009, 38(9): 2359-2362. (in Chinese)

[11] 薛峰, 操乐林, 张伟. 点扩散函数对点目标探测性能的影响分析[J]. 红外与激光工程, 2007, 36(S2): 177-181. XUE Feng, CAO Yuelin, ZHANG Wei. Research on Effect of PSF on Point Target Detection Performance[J]. Infrared and Laser Engineering, 2007, 36(S2): 177-181. (in Chinese)

[12] CASEY E J, KAFESJIAN S L. Infrared Sensor Modeling for Improved System Design[C]// Infrared Imaging Systems: Design, Analysis, Modeling, and Testing VII. Orlando, FL United States: International Society for Optics and Photonics, 1996.

[13] 张科科, 傅丹鹰, 周峰, 等. 空间目标可见光相机探测能力理论计算方法研究[J]. 航天返回与遥感, 2006, 27(4): 22-26. ZHANG Keke, FU Danying, ZHOU Feng, et al. The Study on Detect Ability Calculation Method of Space Object Visible Camera[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(4): 22-26. (in Chinese)

[14] COTA S A, KALMAN L S, KELLER R A. Advanced Sensor-simulation Capability[C]// Signal and Image Processing Systems Performance Evaluation. Orlando, FL, United States: International Society for Optics and Photonics, 1990.

[15] 羊国光, 宋菲君. 高等物理光学第二版[M]. 中国科学技术大学出版社, 2008: 92-96. YANG Guoguang, SONG Feijun. Advanced Physics Optics (Second Edition)[M]. University of Science & Technology China Press, 2008: 92-96. (in Chinese)

[16] 马文坡. 航天光学遥感技术[M]. 中国科学技术出版社, 2011: 76-78. MA Wenpo. Space Optical Remote Sensing Technology[M]. China Science & Technology Press, 2011: 76-78. (in Chinese)

[17] 张兰庆. 基于星载TDI CCD相机动态成像质量的分析与仿真[D]. 哈尔滨工业大学, 2012: 17-18. ZHANG Lanqing. Analysis and Simulation of Dynamic Image Captured by Satellite-based TDICCD Camera[D]. Harbin Harbin Institute of Technology, 2012: 17-18. (in Chinese)

[18] 胡超, 王小勇, 郭崇岭. 应用相位相关法的TDICCD空间相机像移测量方法[J]. 航天器工程, 2014, 23(3): 29-36. HU Chao, WANG Xiaoyong, GUO Chongling. TDICCD Space Camera Image Motion Measurement Based on Phase Correlation[J]. Spacecraft Engineering, 2014, 23(3): 29-36. (in Chinese)

[19] 王铁兵, 李淼, 林再平. 过采样扫描探测性能对比分析[J]. 红外与毫米波学报, 2015, 34(1): 87-91. WANG Tiebing, LI Miao, LIN Zaiping. Comparative Performance Analysis of Over-sampling Scanning[J]. Journal of Infrared and Millimeter Waves, 2015, 34(1): 87-91. (in Chinese)

[20] 杨天远, 周峰, 行麦玲. 空间扫描相机点目标采样系统设计[J]. 航天返回与遥感, 2016, 37(2): 82-91. YANG Tianyuan, ZHOU Feng, XING Mailing. Design of Point Target Sampling System of Space Scanning Camera[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(2): 82-91. (in Chinese)

（编辑：庞冰）

IFOV Optimization Model for Space-based Infrared Point Target Detection System

TONG Xiliang1,2ZHOU Feng1

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（2Beijing Key Laboratory of Advanced Optical Remote Sensing Technology, Beijing 100094, China）

Instantaneous Filed of View (IFOV) is a key parameter for space-based infrared point target detection system. An appropriate IFOV should be selected for a caliber limited space camera to achieve high SNR. The influence of IFOV on energy concentration, sampling phase factor, background clutter and SNR is discussed for a diffraction limited system. An IFOV optimization model is proposed to achieve the maximum SNR. Clutter quantification is executed based on background images, and then clutter coefficient range and distribution are gained. A simulation is conducted based on the model and example parameters. Conclusions are obtained as follows: decrease of IFOV results in energy concentration falling, detection stability getting better and clutter fading down. SNR increases at first and then decreases as IFOV getting smaller. An optimal IFOV is found in the end. The proposed model can be applied to parameter design and optimization of space camera.

instantaneous field of view (IFOV); sampling phase factor; energy concentration; infrared waveband; point target detection; space camera

TP391.41

A

1009-8518(2017)06-0054-11

10.3969/j.issn.1009-8518.2017.06.007

童锡良，男，1989年生，2014年获北京理工大学光学工程专业硕士学位，现为中国空间技术研究院飞行器设计专业博士研究生。研究方向为红外点目标探测遥感载荷总体设计。E-mail：xltong1230@163.com。

2017-08-07