基于激光跟踪仪的多立方镜姿态标定方法
刘 流 侯茂盛 林雪竹 王 强 李丽娟
(长春理工大学光电工程学院,长春 130022)
1 引 言
随着现代工业的快速发展,对工业测量提出了越来越高的要求,特别是航空航天领域。在航天器装调及实验阶段,对产品装星姿态标定测量提出了高精度、高效率的需求。所谓姿态测量是指利用一定的工具对某特定部件进行测量,并用一定方法建立该部件在参考坐标系下的角度坐标系。现有测量方法均为借助立方镜实现对精密部件的测量。立方镜大多是经过精密加工的10mm×10mm×10mm的石英晶体六面体,且镀有反射膜,其相邻两个面有着较高的垂直度,一般垂直度误差不超过3″,这样立方镜的三个相邻面的法线即可构成一个角度坐标系。
国内外均采用电子经纬仪的自准直原理对立方镜的姿态进行测量。长春光机所、解放军信息工程大学以及哈尔滨工业大学的相关研究人员利用Wild T3A,Lecia T3000A, 5100、6100等电子经纬仪的组网互瞄和自准直原理进行立方镜姿态的测量和立方镜坐标系间转换矩阵的标定[1]。在自准直测量过程中,将经纬仪的望远镜调焦至无穷远,由自准直灯发出的光经过聚焦镜和45°半反半透棱镜后,照射在十字丝分划板上,十字丝分划板位于经纬仪物镜的焦平面上,如果经纬仪的视准轴和平面镜的法方向平行,则分划板上十字丝刻划线所成的像经过物镜后形成一束平行光,平行光照射到平面镜上,反射后的像成像在分划板上,并且与原像重合,从而实现经纬仪的自准直测量。然后,通过测量经纬仪的水平角和垂直角度值,即可得到平面镜的法线方向[2]。
具体测量过程包括:经纬仪准直测量、经纬仪互瞄测量、立方镜坐标系的建立与转换。经纬仪互瞄测量是传递准直观测量、建立坐标系的关键,但由于观测现场环境复杂,测量空间狭小,经纬仪间无法通视,需多台经纬仪进行互瞄、建站,从而引入更多的不确定因素和更多的误差,且操作困难。此外,由于立方镜的尺寸较小,增大了经纬仪准直测量的难度,使经纬仪必须多次移动、建站、准直,过程反复,操作强度大,测量效率低。近两年来,哈尔滨工业大学、解放军信息工程大学等利用联合标尺[3]、激光跟踪仪[4]、iGPS测量系统[5]来改进电子经纬仪互瞄的工作,但其测量本质仍旧为电子经纬仪自准直测量原理。
本文在分析了传统准直测量的基础上,改进了测量方法,利用反射、平面镜光学成像原理,使用激光跟踪仪对立方镜姿态进行测量,建立立方镜的坐标系,标定立方镜坐标系间的转换矩阵。
2 测量的原理和方案
2.1 立方镜姿态测量原理
API激光跟踪仪测量立方镜姿态是利用平面镜光学成像原理。首先测量激光跟踪仪靶球在立方镜一个镜面成像的像点,然后测量该像点所在的物点,激光跟踪仪的一束光照射在立方镜镜面上,经镜面反射由激光跟踪仪靶球接收,固定靶球的位置,并测量该靶球的坐标值,即为像点测量;激光跟踪仪不经过镜面反射,直接测量像点固定的靶球坐标值,即为物点测量;由像点物点的连线确定一条直线,即为该立方镜一个镜面的法线。如图1、图2所示。
2.2 立方镜姿态测量方案
由于所使用的立方镜是一个较为标准的镜面正方体,其相邻两个面的垂直误差不超过2″因此可以通过对立方镜相邻两个面法线进行测量以确定两个相互垂直的轴向,将两法线叉乘确定第三个轴向。
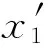
镜面的法线由下式得出

(1)
如图3所示。
3 立方镜姿态测量及转换矩阵的标定
3.1 跟踪仪测量系统对立方镜坐标姿态的测量
激光跟踪测量系统的本质是一种球坐标测量系统,如图4所示,其基本原理是测量与目标点的距离d及水平方向和垂直方向的偏转角α、β,距离分量d由激光干涉仪测量,角度分量α、β由高精度测角装置如圆光栅、编码器等测量。目标点空间坐标P可由公式P(x,y,z)=F(d,α,β)表示,而各分量可由公式(1)给出

(2)
激光跟踪仪对立方镜1的两个互相垂直的表面,镜面A和镜面B的法线进行测量,记录镜面像点和物点的坐标值,利用公式(1)可求得立方镜1两个互相垂直的镜面的法线,如图5所示,然后得到镜面A和镜面B的空间夹角α1。
立方镜1镜面A法线为a1,立方镜1镜面B法线为a2,则两镜面的空间夹角α1
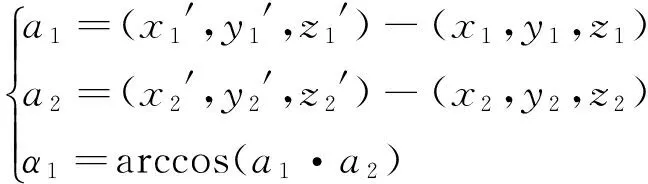
(3)
立方镜2两个互相垂直的表面,镜面C和镜面D的空间夹角α2的测量方法与立方镜1相同。

(4)
3.2 立方镜坐标系间转换矩阵的标定
针对不同的情况,描述坐标转换的方法有很多,如方向余弦法、欧拉描述法、四元数描述法、齐次坐标法、罗德里格矩阵法等[6]。
欧拉角描述法实质是直接迭代欧拉角微分方程,但是当转动规则中的第二次基本旋转接近90°的时候,第一次和第三次基本旋转将变得作用相同(万向锁现象),因此欧拉角法应用受到一定的限制。本文采用方向余弦法进行立方镜姿态的计算,通过迭代姿态矩阵微分方程求解姿态,计算过程不受角度限制且利用方向余弦矩阵表示两个坐标系之间的关系更加直观。
方向余弦法
根据公式(2)对立方镜1法线的计算,可以计算出y轴方向余弦和z轴方向余弦,然后得到x轴方向余弦
(5)
式中:αx——立方镜1坐标系的X轴相对于激光跟踪仪坐标系x轴的夹角;αy——立方镜1坐标系的X轴相对于激光跟踪仪坐标系y轴的夹角;αz——立方镜1坐标系的X轴相对于激光跟踪仪坐标系z轴的夹角;βx——立方镜1坐标系的Y轴相对于激光跟踪仪坐标系x轴的夹角;βy——立方镜1坐标系的Y轴相对于激光跟踪仪坐标系y轴的夹角;βz——立方镜1坐标系的Y轴相对于激光跟踪仪坐标系z轴的夹角;γx——立方镜1坐标系的Z轴相对于激光跟踪仪坐标系x轴的夹角;γy——立方镜1坐标系的Z轴相对于激光跟踪仪坐标系y轴的夹角;γz——立方镜1坐标系的Z轴相对于激光跟踪仪坐标系z轴的夹角[7]。
得到激光跟踪仪坐标系到立方镜1坐标系的旋转矩阵R1为
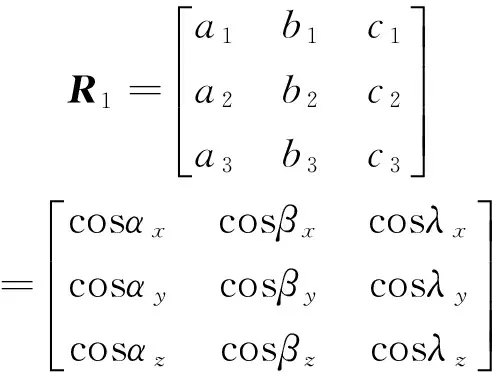
(6)
该矩阵表示了两个坐标系之间的相互关系,实际上该矩阵就是复合变换法中的旋转矩阵M,旋转参数Rx,Ry,Rz通过下式反求得到
同样的方法建立立方镜2的坐标系,确定立方镜2的旋转矩阵R2。
求出立方镜1坐标系和立方镜2坐标系之间的旋转矩阵R为
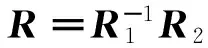
(7)
4 实验及验证
为了验证基于跟踪仪的多个立方镜旋转矩阵标定方法的精度,本文设计了两组实验,分别验证该方法的可行性和标定精度。
4.1 可行性验证实验
将立方镜固定在平整稳固的光学平台上,并保证全部测量流程在隔震基地进行。
第一步,将激光跟踪仪放置在通视范围良好的地点,打开激光跟踪仪进行预热,将激光跟踪仪自带的环境补偿传感器放置在激光跟踪仪发射法附近;
第二步,将激光跟踪仪进行校准,保证测量精度;
第三步,使用激光跟踪仪对立方镜1的面A的法线进行测量,记录像点、物点的坐标值,如表1、表2所示;
第四步,使用激光跟踪仪对立方镜1的面B的法线进行测量,记录像点、物点的坐标值,如表3、表4所示;
第五步,将以上第三步与第四步重复进行十次;
第六步,利用激光跟踪仪测得的像点、物点坐标值建立镜面法线,计算两条法线的空间夹角。

表1 立方镜1镜面A的像点坐标值Table 1 Image point coordinates of mirror A of cubic mirror 1 (mm)
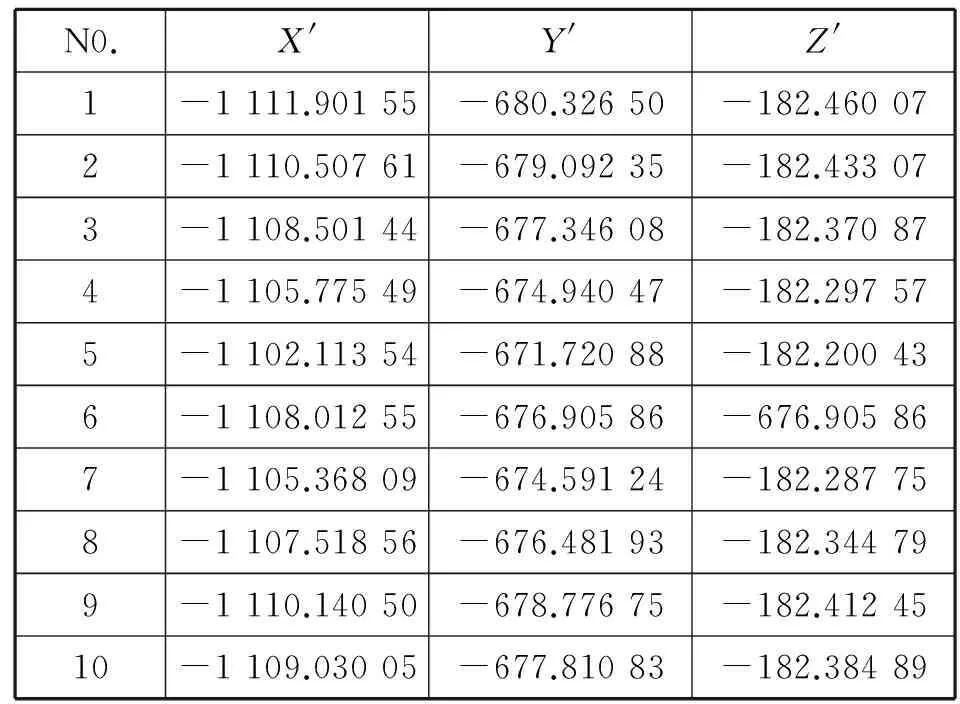
表2 立方镜1镜面A的物点坐标值Table 2 Object point coordinates of mirror A of cubic mirror 1 (mm)

表3 立方镜1镜面B的像点坐标值Table 3 Image point coordinates of mirror B of cubic mirror 1 (mm)

表4 立方镜1镜面B的物点坐标值Table 4 Object point coordinates of mirror B of cubic mirror 1 (mm)
根据立方镜1两镜面像点、物点的坐标值,计算两镜面的夹角,如表5所示。
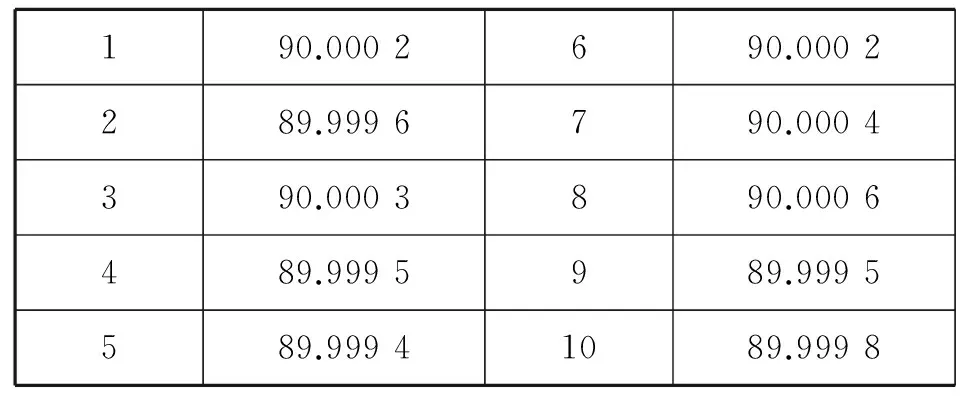
表5 立方镜1镜面A与镜面B的夹角Table 5 Angle between mirror A and mirror B of cubic mirror 1 (°)
实验所用的立方镜镜面夹角标称为90°±3″,使用两台徕卡TM6100经纬仪对上述实验室中的立方镜1的镜面A和镜面B进行自准直测量,两台经纬仪进行互瞄,建立转换矩阵。测得立方镜1的镜面A和镜面B的夹角为90.000 2°。
由以上数据计算出激光跟踪仪所测得立方镜1的镜面A与镜面B夹角的最大偏差为0.000 6°=2.16″,满足测量要求,该测量方法可行。
4.2 重复性验证实
第一步,将激光跟踪仪放置在通视范围良好的地点,打开激光跟踪仪进行预热,将激光跟踪仪自带的环境补偿传感器放置在激光跟踪仪发射法附近;
第二步,将激光跟踪仪进行校准,保证测量精度;
第三步,使用激光跟踪仪对立方镜1的面A的法线进行测量,记录像点、物点的坐标值;
第四步,使用激光跟踪仪对立方镜1的面B的法线进行测量,记录像点、物点的坐标值;
第五步,使用激光跟踪仪对立方镜2的面C的法线进行测量,记录像点、物点的坐标值;
第六步,使用激光跟踪仪对立方镜2的面D的法线进行测量,记录像点、物点的坐标值;
第七步,将以上三、四、五、六步重复进行十次;
第八步,利用激光跟踪仪测得的像点、物点坐标值计算出镜面法线,建立立方镜1、2的角度坐标系,确立立方镜1坐标系与立方镜2坐标系的旋转矩阵,如图6所示。两立方镜坐标轴夹角及方差如表6和表7所示。
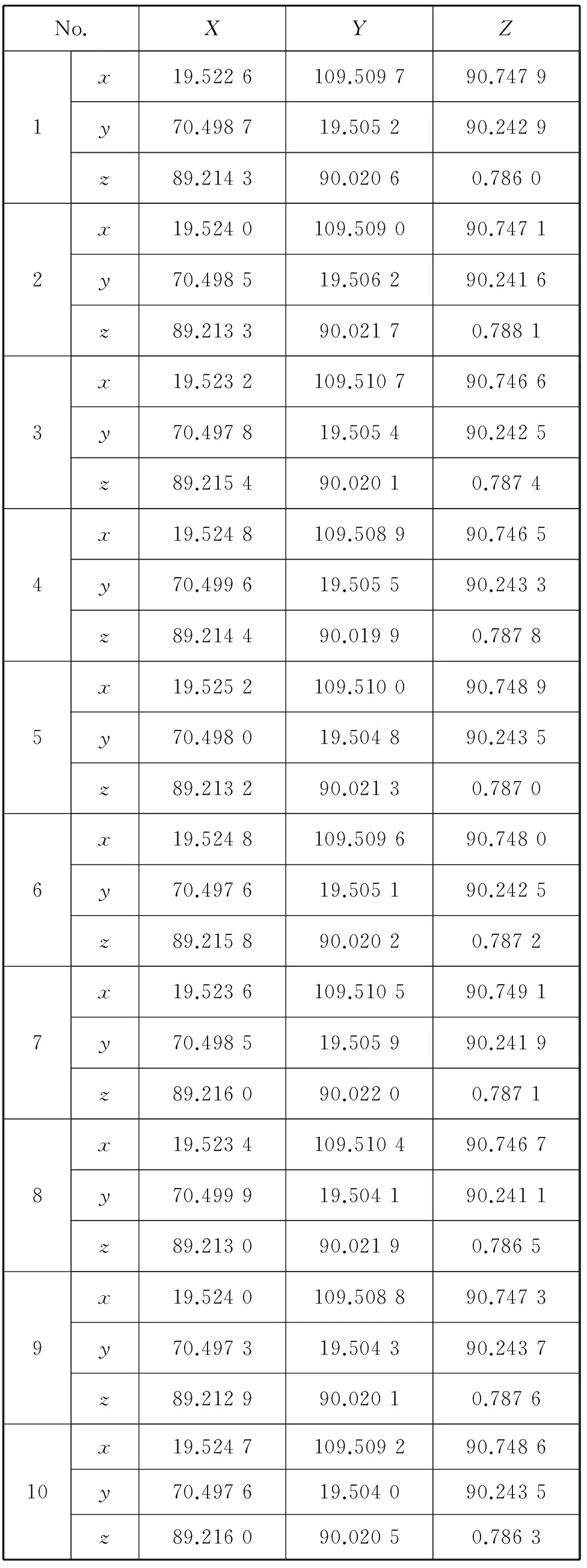
表6 立方镜1与立方镜2坐标轴夹角数据Table 6 Axis angle between cubic mirror 1 and cubic mirror 2 (°)
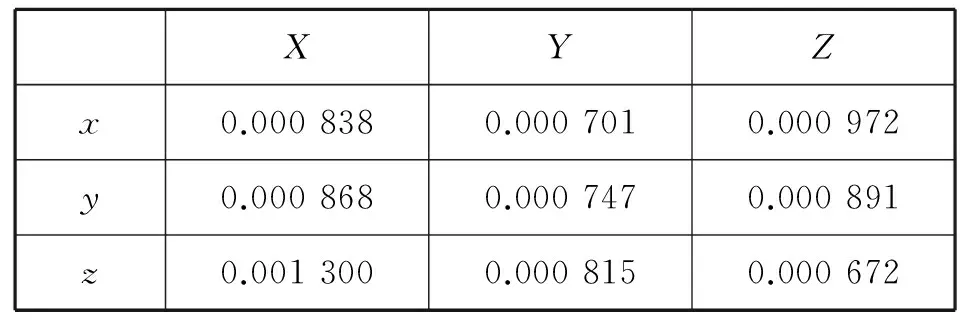
XYZx0.0008380.0007010.000972y0.0008680.0007470.000891z0.0013000.0008150.000672
由上表方差矩阵可以看出,标定误差最大为0.001 300°=4.68″,满足标定精度的技术要求。
激光跟踪仪所配备的环境气象测量传感器,能够进行自检补偿,不断地修正环境因素对测量结果造成的影响。为了尽量的避免和减小误差,激光跟踪仪进行设备反光镜现场检测、ADM现场检测、中间补偿、全补偿等。
由于工作环境的限制,两个立方镜的4个镜面很难在激光跟踪仪的一个站位下均可测得。需要激光跟踪仪转站对上一站位无法测得的立方镜镜面法线进行测量。激光跟踪仪转站过程中一般设立几个公共点,不同站位的激光跟踪仪通过测量公共点,标定出不同站位之间的相对位置关系。激光跟踪仪统一坐标系后继续对立方镜镜面法线进行测量。
5 结束语
(1)基于反射与光学镜面成像原理,使用激光跟踪仪测量立方镜法线,建立了两个立方镜坐标系间的转换矩阵的标定数学模型,并明确了测量方案和测量流程。
(2)通过实验验证分析可知,利用API激光跟踪仪对立方镜姿态进行测量可以建立精确的立方镜坐标系,并且标定立方镜坐标系间的转换矩阵。测量精度优于5″,满足立体测绘的使用要求,整体测量方案可行。方法简洁快速,效率高,大大减少工作强度。
[1] 杨振, 李广云, 范百兴等. 多种互瞄条件下立方镜准直传递方法研究[J]. 宇航计测技术,2013(6): 10~12.
[2] HU Y, HU X, WANG X Y. The influence of drift angle on satellite photography of Three-line array camera[J]. Science of Surveying and Mapping, 2006,31(4):62~63.
[3] 肖华杰, 范百兴, 西勤等. 基于多标尺联合标定的经纬仪测量系统精度分析[J]. 北京测绘, 2016(2): 27~31.
[4] 王凤斌, 梁小峰, 曾森等. 基于公共点转换原理的综合精度检测方法研究[J]. 空间电子技术, 2016,13(4): 91~94.
[5] 杨振, 易旺民, 范百兴等. iGPS系统与经纬仪测量系统联合测量方法研究[J]. 宇航计测技术, 2016(4): 27~31.
[6] 吴国栋. 星敏感器坐标系与自身立方镜坐标系间转换矩阵的标定方法[J]. 仪器仪表学报, 2011,32(6): 135~138.
[7] 柏宏武, 冀有志. 立方镜在航天器天线总装测量中的应用[J]. 空间电子技术, 2013(2): 58~62.

