双相机工业摄影测量系统精度影响几何因素测评

马彤彤 轩亚兵 王伟峰 黄桂平

(1.华北水利水电大学，郑州 450045； 2.郑州辰维科技股份有限公司，郑州 450001)

1 引 言

随着现代先进制造业的发展，工业摄影测量技术已广泛应用于几何尺寸测量，精密零部件形状测量以及产品的三维外形检测等领域[1～3]。同时，不同的测量环境与需求也对工业摄影测量技术提出了更高的要求，双相机工业摄影测量系统也就是在这样的需求下应运而生。

双相机工业摄影测量系统(以下简称双相机测量系统)的理论基础是双目立体视觉理论。20世纪80年代，美国麻省理工学院学者Mart提出了一种视觉计算理论，推动了双目立体视觉理论的发展。90年代后，双相机测量系统开始出现，典型的代表有美国GSI公司的V-STARS/M系统，德国Gom公司的PONTOS系统，此时双相机测量系统分精度在10m以内可达(0. 01～0. 1)mm[4]。

国外学者对双相机测量系统研究起步较早，Sansoni G等人提出了基于主动立体视觉检测物体表面形状的方法Kosmopoulos D等人利用立体视觉技术实现了轿车装配过程中的缝隙实时检测[5,6]；也有相关学者对双相机的检校进行了研究[7,8]。但这些关注的是图像后期处理精度。我国双相机测量系统研究起步较晚，黄桂平对双相机工业摄影测量系统的测量的原理进行了分析[11]。李海滨等分析了双相机测量系统的匹配误差，于英对双相机测量系统的相机标定、图像获取、特征提取与匹配等进行了研究[1]。丁莹从分辨率、镜头焦距、光圈等方面研究并进行了优化[10]。以上研究关注的问题主要是图像算法优化、相机系统误差等，关于双相机测量系统几何网形对点位精度的影响鲜有提及。在实际应用中，大多数测量系统的测量网形通常是根据人为经验来选择的，很少有可借鉴的理论依据[11]，因此研究几何网形因素对双相机工业摄影测量系统点位测量精度的影响很有意义。

本文针对基线长度、摄影距离、摄影光轴与基线的夹角变化等几何因素对双相机测量系统精度的影响进行了一系列的实验研究。通过对实验数据的对比，分析出三个影响因素对精度影响的大小，并以此为依据给出了双相机测量系统测量时这三个因素的最优范围。结合此结论，可以在测量设备固定的条件下通过优化几何网形提高测量精度。

2 精度测评原理

2.1 双相机工业摄影测量系统原理

双相机工业摄影测量系统由两台测量相机组成，根据空间点在两台相机成像平面上成像位置的不同，通过对同名点进行识别与计算从而得到空间点的三维位置信息[9]。具体原理如图1所示，利用两台相机对目标场景进行同时同步拍摄，获得被测物体的图像；然后对特征标志点进行识别，通过特征提取得到标志点的图像中心；最后经过特征匹配、光束法平差计算等步骤，得到待测点精确的三维坐标。通过对标志点三维坐标测量可以实现对静态目标的平面度测量，隐藏点测量以及动态目标的运动状态测量等测量需求。

2.2 精度测评原理

2.2.1 测量重复性评定

精度测试的评定指标选用的是标志点的三维坐标测量精度和系统的测量重复性。系统的测量重复性反应的是系统的稳定性。标志点的三维坐标测量精度反映的是双相机系统的测量能力。

测量重复性测试时连续拍摄六组，然后在每组间进行公共点转换。在公共点转换时，一般以第一组标志点的坐标为基准进行转换。σi(X)、σi(Y)、σi(Z)分别表示第i组测量值相对于第一组在X、Y、Z方向上的点位偏差，则点位标准偏差为

(1)

将所有组的点位标准偏差的结果求取平均值，(本次试验重复性比较RMS在20μm以内，满足要求)该值越小说明双相机测量系统的稳定性越高。

2.2.2 三维坐标测量精度评定

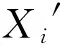
(2)

(3)

(4)

(5)

式中：n——公共点的个数；Δdi——双相机相对于单相机的第i个公共点的点位偏差；σ——双相机相对于单相机的点位偏差的均方根值；mM——双相机系统的点位测量精度；mS——单相机系统的点位测量精度。

测试采用郑州辰维科技股份有限公司的单相机测量系统MPS/S36为标准，对双相机系统的测量精度进行评价。MPS/S36的标称精度为5μm+5μm/m，且已经经过大量的验证[13]，远高于双相机的标称精度20μm+16μm/m。按照式(3)得到点位偏差的均方根值σ，单相机的标称精度已知且小于双相机的三分之一，根据误差理论，σ近似等于双相机系统的点位测量精度。由此可以推出点位偏差的均方根值σ的值越小，双相机的三维坐标测量精度越高[13]。

2.3 影响精度的几何因素

数字近景工业摄影测量系统的精度与诸多因素有关，如光照强度，温度等外界条件影响；相机自身的稳定性以及相机标定结果的好坏等相机自身条件影响；摄影闪光灯的强度，操作人员的拍摄技巧等人为的影响。除了以上影响因素之外，还有一个很重要的因素就是测量时的几何网形，即拍摄时测量对象与相机设站之间的相对位置关系。

双相机工业摄影测量根本原理是三角交会原理，每一个待测点至少要被两条摄影光束相交才可解，因此受到两相机摄影光轴间交会角的影响。理论上讲交会角为90时测量精度最好，交会角变小或变大其精度也变低[9]。交会图形X、Y方向误差影响如图2所示。

相机的像点坐标测量精度一样的情况下，测量几何网形的布设不同，其测量结果精度甚至会相差十倍[2]。双相机的交会角度受诸多几何条件的制约，如两台相机的基线长度、摄影距离等。本文在理论分析基础上，为了进一步验证双相机测量系统的几何因素对测量精度产生的影响，设计了改变基线长度，摄影距离，基线偏离检定墙中轴线的距离三个方面的实验。

3 试验设计与数据分析

实验测量对象为一稳定墙面，测量范围是3.3m×1.8m，如图3所示。墙上共135个编码点，均匀分布358个单点，如图4所示，所有的点均为摄影测量回光反射标志点。首先对测试的墙面进行多组测量，然后以其中一组作为标准进行公共点转换，将其他组测量结果转换到第一组的坐标系下，方可进行比对。使用郑州辰维科技股份有限公司自主研发的MPS/M04双相机工业摄影测量系统进行实验，如图5所示。

实验过程中分别用单、双相机进行拍摄。单相机采用9点法拍摄[13]，并进行重复性测量，以保证其精确度。双相机拍摄墙上的点时，每台相机同时同步连续拍摄3张像片。为验证两台相机之间的位置关系对最终的测量结果所产生的影响[11]，在对双相机测试时将其他影响因素降低到最小，考虑光线条件等外界因素影响，每组测量应在短时间内完成并将闪光灯指数调整到最佳(在图像中观察到标志点灰度值为200以上并保证其不曝光过度)，然后利用双相机系统软件对三组拍摄到的同名点的点位坐标进行误差对比，得到双相机的点位精度。比较三组测量结果，取平均值。三组实验内容如下。

3.1 基线长度的影响实验

基线长度是两相机之间相互位置的重要参数，它的变化会引起系统结构的改变，进而直接影响测量精度。因此根据实验场大小和工程经验首先固定摄影距离为3m，其他因素保持不变，根据实验场地空间适当改变基线长度，并保证两台相机相对检定墙的中轴线对称，并将结果与高精度单相机点位坐标测量值进行公共点转换。基线设计成由1m，2m,…,9m均匀变化的九组实验(如图6)，研究基线长度对点位精度的影响,具体试验结果见表1。

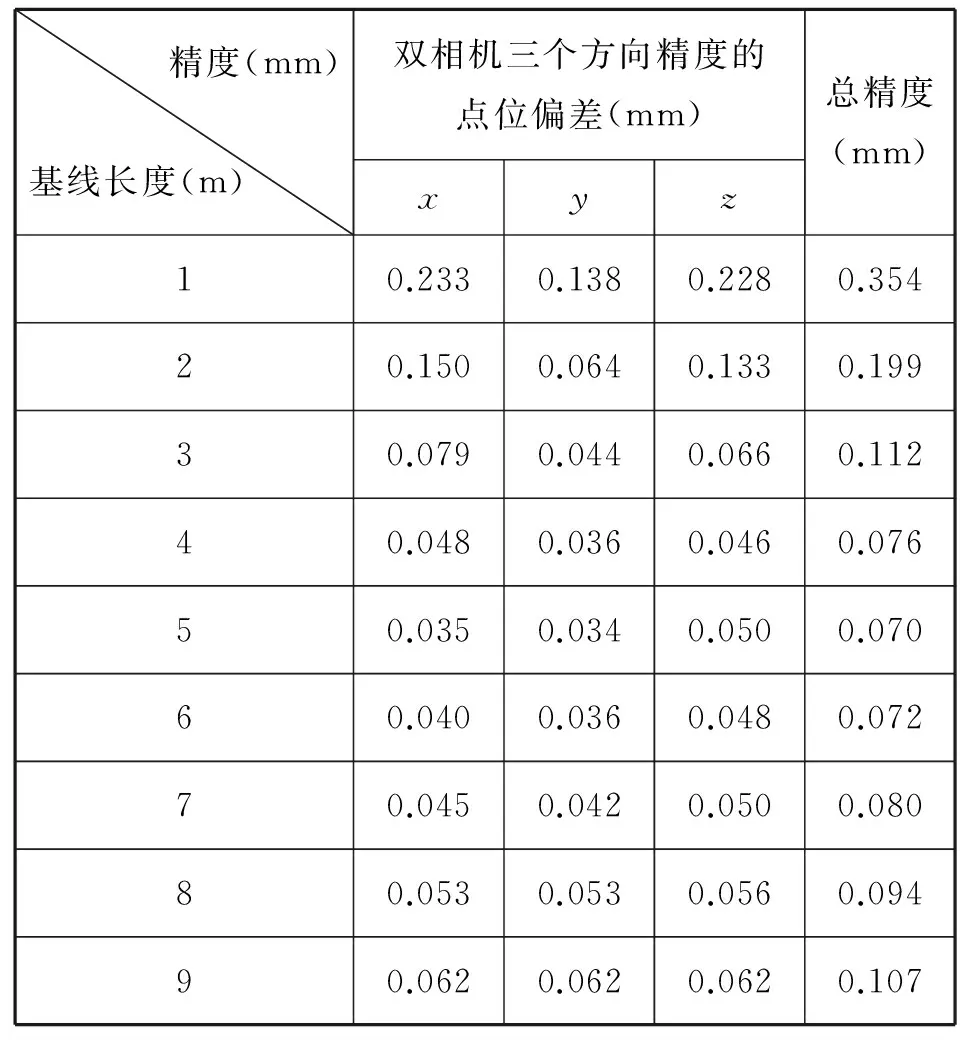
精度(mm)基线长度(m)双相机三个方向精度的点位偏差(mm)xyz总精度(mm)10.2330.1380.2280.35420.1500.0640.1330.19930.0790.0440.0660.11240.0480.0360.0460.07650.0350.0340.0500.07060.0400.0360.0480.07270.0450.0420.0500.08080.0530.0530.0560.09490.0620.0620.0620.107

从表1可以看出，x,y,z三个方向及总点位精度的大小范围呈同一趋势变化，随着基线长度的增加迅速减小后又缓慢增加，在一定的范围内(4m～6m)点位精度值呈现最佳状态(说明此状态下的双相机测量精确度最高)。为更直观的的分析，制作出点位精度分析图，如图7所示。

3.2 摄影距离的影响实验

摄影距离的变化会影响双相机拍摄识别点位的数目(距离过近易引起曝光过度，过远会使点位拍摄不清晰)。为减化方案，跟据实验一结果，设置基线长度为5m，根据实验场地将摄影距离均匀改变十一组值，依次设为1.5m，2.0m,…,6.5m(如图8)，每次实验均将闪光灯指数调整到最优，观察数据，分析最佳摄影距离范围，相关数据结果见表2。

从表2数据分析可以看出，当基线长度一定，其他外界条件不变，摄影距离在2m～3m时其总点位精度较高，摄影距离过近或过远均不能达到良好效果，当距离达到6m时偏差陡然增加，大于此距离将无法获得好的点位精度。根据表2制作出总体精度趋势曲线图，如图9所示。

3.3 基线偏离检定场中轴线位置的影响实验

实验过程中为避免干扰因素存在而造成误差，将闪光灯指数设置为固定值10。根据实验一、二结论，基线长度调整为最优值5m，摄影距离调整为3m。将固定好基线长度的双相机作为一个整体，相机初始位置在检定场中轴线处对称放置。实验过程中沿基线所在方向左右依次等距离变化(0.5m，1.0m,…,2.5m)五组，(如图10,以右移为例)。观察基线偏离中心对点位精度产生的影响， 测试数据见表3。

根据表3可知，当双相机系统与固定的基线作为整体进行偏移时会使点位总精度呈现规律性变化，即随着基线的移动，总精度及三个方向的点位精度都随着左右偏向距离的增大而降低。同时当固定摄影距离、基线长度及其他影响因素的情况下双相机两光轴所夹的交会角度也随之变化。由表3制作出基线偏离中轴线对点位精度影响的曲线图(如图11、图12)，可直观地发现基线整体左偏时X方向点位精度变化较Y，Z方向的明显些，右偏则Z方向更为明显，但两个方向偏移的总精度变化均偏差不大，且趋势走向一致。

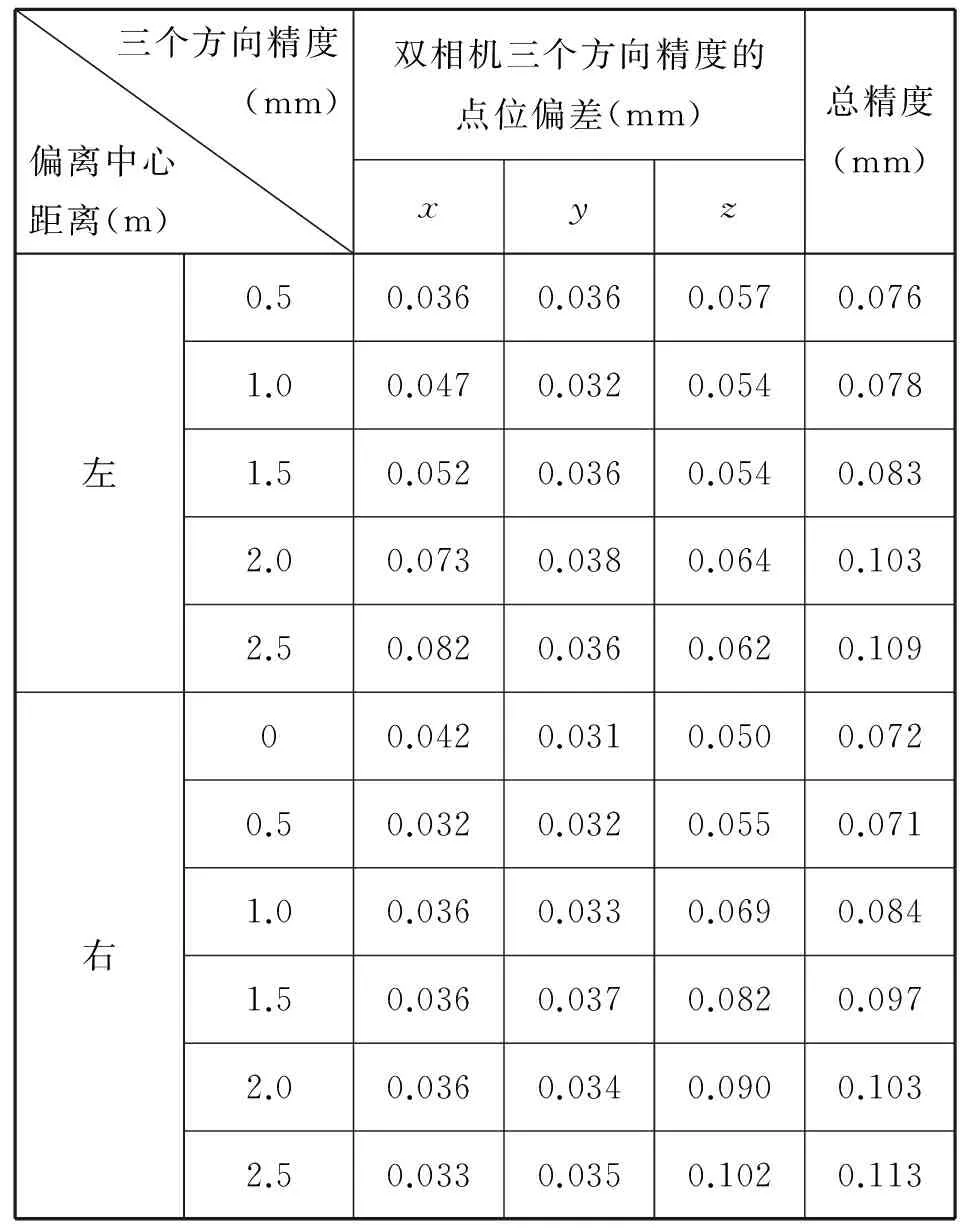
表3 基线偏离检定场中轴线位置对测量精度影响Table 3 Baseline deviation from the test field axis position on the measurement accuracy

4 结束语

通过对双相机测量系统工作原理的分析，重点研究了双相机测量系统的几何因素对测量精度的影响。实验证明双相机测量系统精度受几何网形变化的影响非常明显。其中在试验场固定3.3m×1.8m的情况下，基线长度前后对比偏差达0.284mm，摄影距离偏差达到0.183mm，基线偏离检定场中轴线的位置影响较小，为0.041mm，且实验中发现三者均与双相机光轴之间的交会角度存在约束性关系。

此外，通过与被测对象的尺寸进行对比分析实验还可以得出以下结论：(1)基线长度与控制场长度相差不可过大；(2)摄影距离最好与控制场大小相等或略小；(3)基线偏离检定墙中轴线的距离对点位精度影响不大，但为达到更高的拍摄精度，也应尽量使基线中轴线与检定场中心重合。

本次实验研究了几何因素对双相机测量系统精度的影响，解决了几何网形布设的难题。为今后的双相机拍摄影像应用与几何网形设计提供了良好的借鉴。

[1] 于英.双目立体工业摄影测量关键技术研究与应用[D].解放军信息工程大学，2010.

[2] 黄桂平.近景工业摄影测量关键技术研究与应用[D].天津大学，2005.54～55.

[3] 卢成静，黄桂平，李广云.V-STARS 工业摄影三坐标测量系统精度测试及应用[J].红外与激光工程,2007，36(6):245～249.

[4] Erne 0, Fri ebe H, and Galanulis K.Is it possible to replace conventional displacement and acceleration sensor technology Solution methods using optical 3D measuring technology[EB/OL」.com，2009.

[5] SANSONI G，CAROCCI M，RODELLA R.Calibration and performance evaluation of a 3D imaging sensor based on the projection of structured light[J]． IEEE Transactions on Instrumentation and Measurement，2000，49(3):628～636.

[6] KOSMOPOULOS D VARVARIGOU T.Automated inspection of gaps on the automobile production lineThrough stereo Through stereo vision and specular reflection[J].Computer in Industry，2001，46(1): 49～63.

[7] ParianJA,GruenA.SensoModeling,Self-calibration and Accuracy Testing of Panoramic Cameras and Laser Scanners[J]. ISPRS Journal of Photogrammetry and Remote Sensing，2010，65(1):60～76.

[8] Zhao Ge,LinLan.A New Optimal Seam Finding Method Based on Tensor Analysis for Automatic Panorama Construction[J]. Pattern Recognition Letters，2013(34)：308～314.

[9] 黄桂平.数字近景工业摄影测量理论、方法与应用[M].北京：科学出版社，2016.

[10] 丁莹，范静涛.双目立体视觉检测系统正向最优化设计方法研究[J]．仪 器 仪 表 学 报， 2016，37(3).

[11] 余慧杰，韩平畴.双目视觉系统的测量误差分析[J].光学技术，2007，33(11):157～159.

[12] 刘琼，秦现生，应申等.双目视觉测量系统结构参数设计及精度分析[J].中国机械工程，2008(22)：2 728～2 732.

[13] 轩亚兵，王伟峰，高亚伟，等.国产工业摄影测量相机精度测评[J].宇航计测技术，2015，35(4):14～18.