初中数学从“知识课堂”到“探究课堂”的思考

江勤娟

[摘 要] 注重生本课堂的价值达成，就要将数学课堂由原先的“知识课堂”引领到“探究课堂”中. 我们不仅要从思想意识上全面转变，更要从教学行为中真正落实到行动中，让探究性学习落到实处，并将探究性思维渗透到学习行为中.

[关键词] 探究；思维；递进；初中数学

随着素质教育的实施和推进，课堂教学模式也发生了翻天覆地的变化. 原来传统的“知识课堂”正在向“探究课堂”转变，这种转变不再是因为上级教育主管部门要检查，而是因为学生和教师在求知与教学过程中实实在在地需要. 在知识与技能的建构上，在问题与质疑的解决上，探究性思维与行为决定着学习的高度与深度，决定着学习的效果与价值. 因此，在这种探究性学习背景下，师生之间的地位变得越来越平等，学生的主体作用得以发挥. 但是，这种课堂模式的转型并不是随意就能完成的，而是需要师生之间共同配合，利用探究性教学活动，一步一步地实现探究课堂.

创设探究情境，激发探究欲望

在当前的教学模式下，情境教学法已经成为主要的教学方法之一. 为了能够实现初中数学课堂向探究课堂的转变，教师可以利用创设探究情境的方式，激发学生的探究欲望. 在科学、合理的教学情境中，学生的积极性能够得到调动，情感状态也能更加饱满，对数学知识进行探究也会更有效率. 而教师则需要选择合适的情境来迎合教学目标的达成，对接学生学习兴趣的激发，引领学生思维的生长.

例如，笔者在开展“整式的加减”教学时，在数学课堂上设计了如下教学情境：

青藏铁路线上，在格尔木到拉萨之间有一段很长的冻土地段. 列车在冻土地段的行驶速度是100千米/时，在非冻土地段的行驶速度可以达到120千米/时. 在西宁到拉萨路段，列车通过非冻土地段所需时间是通过冻土地段所用时间的2.1倍，如果通过冻土地段需要t小时，你能用含t的式子表示这段铁路的全长吗？

问题情境更能激發学生积极思考. 在笔者的引导下，学生进行思考和讨论之后可以得到式子：100t+120×2.1×t. 通过这种创设探究教学情境的方式，既可以对同类项的概念进行学习，又能帮助学生建立符号感，体会整式的加减.

在良好的教学情境中，学生能够对即将要学的数学知识产生探究兴趣，这样一来，便可以积极地发挥学生的主观能动性，让学生进行主动探究.

设置层次问题，循序渐进地探究

探究是一个过程，在这个过程中，学生应当遵循循序渐进的原则. 为了让学生的探究过程更加顺利，更加符合学生自身的心理认知特点以及发展规律，教师可以在课堂上设计一些层次性问题，由浅入深地引导学生循序渐进地进行探究. 在这种梯度性问题的引导下，探究也会一步一步地深入. 而这种梯度也不是一概而论的，教师要充分分析学生的学情和差异，结合学生的实际状况进行调整，以此保障学生在其力所能及的范围内达成思维的递进.

笔者带领学生学习“消元法解二元一次方程组”时，首先给出了这样一道例题：篮球联赛中，每场都要分出胜负，每队胜1场得2分，负1场得1分，某队10场比赛中得到16分，那么这个队的胜、负场数分别是多少？设胜x场，负y场，根据条件，可列出二元一次方程组x+y=10①，2x+y=16②. 随后，笔者提出了第一个问题：你能发现方程组中的两个式子有什么联系吗？经引导，学生发现两个式子中都含有y，由此可以由一个方程得到y的表达式，并把它代入另一个方程，变二元为一元，即可由①得y=10-x③，把③代入②得2x+（10-x）=16，解得x=6. 笔者接着提出第二个问题：你能把③代入①吗？学生试验后发现不能，因为式子会回到原来的模式. 最后，笔者提出了第三个问题：你能求出y的值吗？学生回答：把x=6代入③得y=4.

教师通过这三个不同层次的问题，让学生进一步了解利用消元法解二元一次方程组的关键之处在于“代入”这一步. 在问题的引导下，学生的探究变得更加有规律和方向. 这样一来，学生的学习效率自然能够有所提升，探究也会变得更加简单.

转变教学理念，师生共同探究

在传统的教学模式下，教师一直处于“高高在上”的地位，教师总是主导着整个课堂的进展. 长期处于这种环境之中，学生的主观能动性以及探究欲望就会受到压制，这种情况并不利于探究课堂的形成. 因此，教师应当转变教学理念，让学生做课堂的主人，与学生一起共同探究，提高探究课堂的效率.

笔者在引导学生探究“不等式的性质”时，在课堂上利用天平的变化，促进学生总结不等式的性质. 首先，笔者在天平的两端放置了不同重量的砝码，然后引导学生在天平的两端加上或者减去同等质量的砝码. 在学生的操作下，他们发现这样的操作并不会使天平的方向发生变化，于是我们总结出不等式的第一个基本性质：不等式的两边都加上（或减去）同一个整式，不等号的方向不变. 随后，笔者引导学生对天平进行操作，将天平两端的砝码同时乘或者除以同一个正数，经过操作，学生得出天平的方向依然不变的结论，于是我们又总结出了不等式的第二个基本性质：不等式的两边都乘（或除以）同一个正数，不等号的方向不变.

在教学行为中，教师要努力转变以往的观念，通过对教学理念的转变，让师生可以处在一个平等的地位，并在教师和学生的共同合作探究中，让学生体验到获得知识的乐趣以及探究成功的喜悦. 这样的教学途径，能促进学生意识到自己的主体作用，做学习的主人，做课堂的主人，做积极的探究者.

利用变式训练，培养探究思维

在素质教育不断发展的过程中，培养学生的学习能力已经成为教师的主要教学任务. 要让初中数学课堂从知识课堂向探究课堂转变，就必须让学生意识到探究的重要性. 变式训练的运用，能够有效地培养学生的探究思维，最重要的是，它能够训练学生举一反三的能力，帮助学生理解更多不同类型的数学问题本质，真正引导学生以不变的思想与方法挑战千变万化的问题，真正达到学以致用的效果.endprint

如二次函数问题：已知二次函数的图像经过A（-3，0），B（1，0），C（0，-3）三点，求这个二次函数的解析式. 这个问题比较简单，为了能够提高学生的探究能力，培养学生的探究思维，笔者对这一问题进行了变式.

变式1？摇 已知二次函数的图像经过一次函数y=-x-3的图像与x轴、y轴的交点A，C，且经过点B（1，0），求这个二次函数的解析式.

变式2？摇 已知抛物线经过B（1，0），C（0，-3）两点，且对称轴为直线x=-1，求这个抛物线的解析式.

变式3？摇 已知一次函数的图像经过点（1，0），且y轴上的截距是-1，它与二次函数的图像交于A（1，m），B（n，4）两点，又二次函数的对称轴是直线x=2，求这两个函数的解析式.

对原有问题进行变式之后，问题变得更具曲折性，需要学生进行深入的思考和探究，并结合之前所学的知识，才能顺利解答变式问题. 在做变式训练的过程中，学生的探究思维得到了有效地开发，而知识与技能的深度和广度也得到了有效地训练和变通，学生的学习效能也得到了真正地提升.

给予交流空间，让探究更自由

很多时候，知识课堂无法向探究课堂转型的原因是学生缺乏交流的空间，学生在思维与参与的过程中，缺乏足够的思维空间与时间，这也就意味着学生缺乏探究的自由. 而探究，应当是自由的，学生在一个特定的环境中针对某一个或者多个问题进行探究时，大家应畅所欲言地发表自己对数学知识的理解和看法，在此过程中，学生的思维会得到洗礼，探究能力也会随之提升. 所以，为了形成探究课堂，教师应当给予学生足够的交流空间.

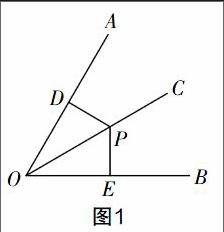
开展“角的平分线性质”教学时，为了能够让学生掌握本节课的重点内容，笔者在课堂上给予了学生充分的时间，引导他们对角平分线的性质进行探究和交流. 课堂上，学生按照笔者的提示将一个角（∠AOB）对折，再折出一个直角三角形，展开之后观察两次折叠形成的三条折痕，在大家的观察和讨论下，得出了这样一个结论：已知一个点在一个角的平分线上，则这个点到这个角两边的距离相等. 随后，笔者又引导学生对这一命題用数学方法进行科学、严谨地求证. 于是，大家画出了图（如图1），并标出相应字母之后进行证明：因为 PD⊥OA，PE⊥OB （已知），所以∠PDO=∠PEO=90°（垂直的定义）. 在△PDO和△PEO中，因为∠PDO=∠PEO（已知），∠AOC=∠BOC（已知），OP=OP（公共边），所以△PDO≌△PEO（AAS）. 所以PD=PE（全等三角形的对应边相等）.

在教师的引导下，给予学生足够的交流空间，让学生进行自主探究或合作交流，这种方式能让学生体会到自己的主体作用，并且可以加深对数学知识的印象. 相信初中生能够对交流的空间进行合理地运用.

总而言之，将知识课堂转化为探究课堂，需要的不仅仅是几个简单的步骤，而是教师对于教学内容以及学生学情的深入了解，是师生双方之间的相互配合，是教学理念的改变，是教学方法的完善和强化. 希望以上几点建议能够为广大教师同行起到一定的帮助作用.endprint