如何在高中数学教学中培养学生解题能力

陈晨

（内蒙古北方重工业集团有限公司第三中学，内蒙古包头 014030）

在高中阶段的教学中，数学是一门重要的基础性学科，加强高中学生解题能力的培养，促使学生数学学习能力和成绩的提高，促进学生逻辑思维能力的提高，促使学生事物分析能力的提高，有利于学生未来的数学学习以及发展。高中数学对学生的逻辑思维能力具有较高的要求，学生在学习的过程中会感到困难和吃力，容易产生抵触的情绪。因此，在实际教学开展的过程中，教师应当对教学方式进行合理的运用，提高课堂教学的有效性，促进学生解题能力的提高，促使课堂教学有效的开展。

1 加强数学基础知识的深入理解

高中数学课堂教学活动开展时，想要提高学生的数学解题能力。首先需要学生对数学基础知识进行学习和理解。在高中数学教学的过程中，大多数的数学题是通过数学的定理、定义等内容进行变形得到的，放在不同的解题情境中形成不同的问题。学生在面临这些问题时，往往难以对问题的本质进行发掘和掌握，其中一点重要的原因就是学生对基础概念和基础知识缺少理解，学习不够扎实。在高中数学教学的过程中，加强对基础知识的强化和练习，促进学生基础知识的夯实，能够更好的融会贯通，促使学生在解题中快速的找到解题的方式和思路。例如，在人教A版高中数学“空间几何体的表面积和体积”的教学中，对学生的空间思维能力具有一定的要求，对于学生来讲是一个陌生的问题，学生难以理解和掌握。因此，教师在教学开展的过程中，根据课堂教学的实际内容，结合学生的实际生活，引导学生对身边的物体进行观察，对学生进行相关知识内容的讲解，促使课堂教学难度的降低，促使学生空间思维能力的提高。同时，教师可以借助实物引导学生和数学例题进行联系，加深学生对体积和表面积的理解，深刻的理解基础知识内涵，促使学生在实际的物体中进行基础知识的掌握，培养学生的空间思维，促使学生思维的转化，有利于学生对基础知识的掌握，促使学生解题能力的提高。

2 促进学生审题能力的提高

在高中数学课堂教学中，教师加强对学生解题能力的培养时，却忽视了学生的审题能力。学生审题能力的不足，常常由于审题错误造成解题错误，在对错题进行解析的过程中，学生才发现并不是题目不会而是由于审题出现错误。所以，在高中数学课堂教学活动开展的过程中，教师应当导引学生对数学思想方法进行掌握，能够对审题的技巧进行灵活的运用，正确的寻找问题切入点，有效的促进问题的解答，同时在审题的过程中需要对题目中的逻辑关系进行清晰了解，对题目中隐含的条件进行寻找，确保题目能够顺利的解答。例如，在人教A版高中数学必修一“函数与方程”的教学中，教师可以借助例题进行教学。如已知函数f（x）=k x2+（k-3）x+1的图象和x轴在原点的右侧有交点，求解k的取值范围。在面对这样的题目时，需要进行相应的分类讨论，然后对题目进行解答。避免学生对题目不深入的审题就开始解答，导致不能全面的解答问题。因此，在高中数学教学的过程中，教师应当注重学生学习态度的端正，促使学生审题能力的提高，进一步提高学生的解题能力。

3 促使数学思想方法的利用，培养学生解题能力

在高中数学教学的过程中，存在很多的解题思想方法。在高中数学教学的过程中，促使学生能够有效的利用数学思想方法，促使学生对数学基础知识进行掌握，提高学生数学知识的灵活运用能力，促进学生逻辑思维能力的提高，有利于学生创新意识和创新能力的培养，促进学生数学综合素养的提高。在教学的过程中，教师应当对学生的学习实际进行了解，逐渐的增加学习的难度，帮助学生对解题的技巧和方式进行掌握，提高学生的数学思想意识，促使学生解题效率的提高。同时注重学生创新思维和发散思维的培养，促使学生对知识内容和解题方式进行迁移，提高学生的解题能力，提高课堂教学的质量。例题，在直角坐标系平面内两点 P、Q 满足下面的条件：P、Q 在函数 f（x）的图象上；P、Q 关于原点对称，那么称点对（P、Q）是函数 f（x）的一个（友好点对）。已知函数

则f（x）的友好点对有（）个。在对这样的问题进行解决时，需要对问题进行有效的转化，可以对数形结合的思想方法进行利用，对数学问题进行解决，促使学生解题能力的提高，提高课堂教学的有效性。

4 灵活的运用数学知识，培养学生一题多解的能力

在学生解题的过程中，教师需要引导学生对数学知识进行迁移，促使学生能够一题多解，举一反三，提高课堂教学的有效性，促使学生解题能力的提高。培养学生一题多解、举一反三能力时，需要引导学生从不同的角度看待问题，促使学生解题能力的提高。

例如，在人教A版高中数学必修一“对数函数”的教学中，教师可以借助这样的例题进行教学，促使学生能够举一反三，提高学生的解题能力。例题：证明函数的图象关于原点对称。面对这样的例题，学生利用相关知识内容能够很快的解答。

解析：函数的定义域是R，并且

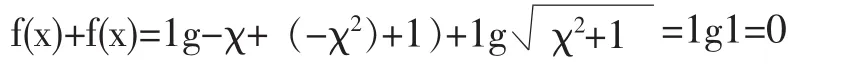
所以 f（-x）=-f（x），所以函数的图象关于原点对称。教师可以对此题进行有效的变化，引导学生进行解答。

变题 1：已知函数 y=f（x）满足 f（-x+1）=-f（x+1），求证：函数 y=f（x）的图象关于（1,0）对称。

变题 2：已知函数 y=f（x）满足 f（x）+f（-x）=2，求证：函数 y=f（x）的图象关于（0,1）对称。

变题 3：已知函数 y=f（x）满足 f（x）+f（2+x）=2，求证：函数 y=f（x）的图象关于（1,1）对称。

5 结语

新课程改革的不断深入，要求高中数学教学不断的创新，教师应当根据实际的特点和要求开展课堂教学。在实际教学的过程中，不仅仅需要学生对知识内容进行掌握，同时需要培养学生的解题能力。在实际教学的过程中，加强学生基础知识的掌握和理解，促进学生审题能力的提高，促使学生数学思想方法的灵活运用，促进学生解题能力的培养，促使问题有效的解决，提高课堂教学的质量。

[1]韩富万.高中数学教学中如何培养学生的解题能力[J].课程教育研究,2015(2):135-136.

[2]徐大伟.在高中数学教学中培养学生的解题能力[J].考试周刊,2017(93):87.

[3]陈建军.在高中数学教学中如何培养学生的解题能力[J].数学学习与研究,2016(17):46.