向量在转向杆系受力分析中的运用

甘林，赵丹，徐垒

（安徽江淮汽车集团股份有限公司，安徽 合肥 230061）

前言

转向系统各零部件的受力分析是零部件设计的主要依据，准确的计算结果可以有效提高材料的利用率，对转向系统的轻量化设计有着不可忽视的作用。

现在对转向系统杆系的受力分析采用平面几何作图的方法，当方向盘旋转一个角度以后，各个零部件均在空间做一个复杂的运动， 现在使用的计算方法只能采取近似计算，计算结果也只是一个近似值。

随着计算机技术的发展，转向系统也实现了三维模拟，通过三维软件可以很容易得到转向系统各杆件连接点坐标，通过向量的运算方法，使用EXCEL作为运算工具，就可以准确快速的计算出各杆件的受力。

1 向量及其运算

1.1 定义

既有大小又有方向且遵循平行四边形定则的量称为向量。分为自由向量与固定向量。自由向量不考虑向量的起点；固定向量确定了向量的起点（或者终点）。

1.2 向量的表示

如上图1所示，点A（x1,y1,z1）、点B（x2,y2,z2）分别为向量a的起点与终点，则向量

1.3 向量的计算

1.3.1 向量的模

向量的模即为向量的长度。已知向量a=（x，y，z），则向量的模：

1.3.2 向量的加法

如图 2所示：a=（x1,y1,z1），b=（x2,y2,z2），a与 b的起点为O点，则

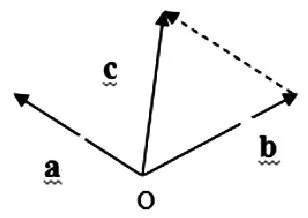
图2 向量的加法

物理意义：已知力a、b，两力的作用点为O，两个力的合力即为c，c的作用点为O。

1.3.3 向量的内积（点乘）

如图 3所示：a=（x1,y1,z1），b=（x2,y2,z2），则：

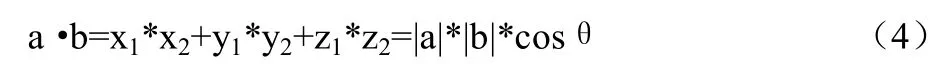
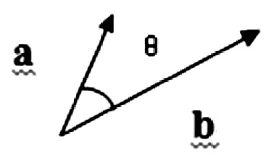
图3 向量内积

向量的内积表示向量a在向量b上的投影长度与向量b的长度的乘积。

1.3.4 向量投影到另一个向量后得到的向量

如图4所示，c为a在b上的投影，已知a和b，c为a在b上的投影。因为a· b=|c|*|b|，

c=|c|*(c/|c|)，c/|c|为c的方向向量，c/|c|=b/|b|，所以：

1.3.5 向量的外积（叉乘）

如图 5所示：a=（x1,y1,z1），b=（x2,y2,z2），a的起点 O，终点为A，b的起点为A，则：

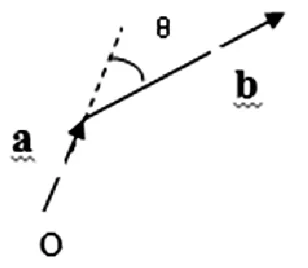
图5 向量的外积

c的大小为| a |*| b |*sinθ；c方向遵循右手定则：a沿小于 180°的方向向 b旋转，大拇指的方向即为 c的方向，c同时与a、b垂直。

c可以用行列式表示

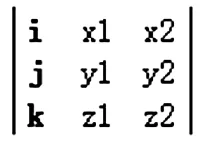
行列式展开为x3i+y3j+z3k，则c=（x3,y3,z3），其中

物理意义：表示力b对点O的力矩，a为力b对点O的半径向量（矢径）。

因为力对轴的矩等于力对该轴上任意点的矩在轴上的投影，所以结合上面的公式，可以利用向量计算任意力对任意轴的力矩。

以上公式均可以通过计算机表格程序编程完成计算。

2 案例分析

2.1 案例

根据需求，为某款轻卡设计转向杆系。转向杆系不但要满足使用要求，还要满足强度要求，所以要对转向杆系强度进行校核，首先需要对转向杆系进行受力分析。

根据设计说明书，该轻卡匹配转向器最大输出力矩为1920N·m。

2.2 受力分析

2.2.1 转向系统状态三维模拟

转向器满足使用要求，即转向器的输出力矩大于等于转向阻力矩。因为液压系统的压力由负载决定，所以只有当转向系统转到极限位置时，系统压力达到最大值，转向器输出力矩达到最大值，需要校核此时转向系统杆系的强度。

根据该车前轴图纸，可知道该车转向限位采用外轮限位，内轮最大转角为31°。以右转为例，该车右转到极限位置时的三维情况如下图6a、图6b所示：

图6 a 转向杆系右转极限位置主视图

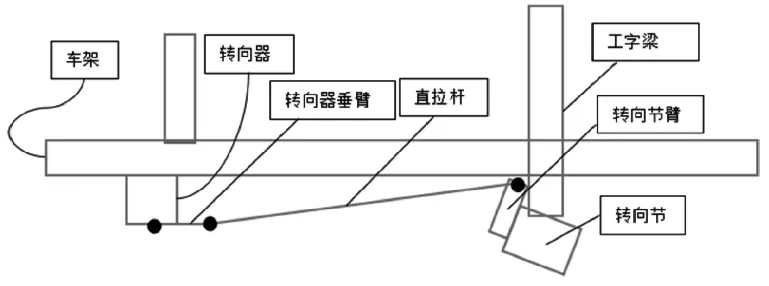
图6 b 转向杆系右转极限位置俯视图

2.2.2 杆件受力状态分析

通过三维数模，我们可以很容易的知道各杆件受力的作用点以及方向，从而要求出力的大小。

转向器垂臂：只有绕转向器输出轴旋转一个自由度，在转向器输出力矩与直拉杆对摇臂球销压力的作用下平衡；

直拉杆：二力杆，在转向器垂臂球销压力与转向节臂球销压力的作用下平衡；

转向节臂、转向节：二者为一固连整体，只有绕主销旋转一个自由度，在转向到极限位置时，转向节相当于固定在工字梁上，此时转向节臂在直拉杆的压力与转向节的支反力作用下平衡。

通过以上分析，只需要计算出直拉杆上的力，就可以分别计算出转向器垂臂、直拉杆、转向节臂的强度是否满足要求。

2.3.3 计算直拉杆受力大小

取直拉杆与转向器垂臂分析，三维如下图7所示：

图7 直拉杆与摇臂相对位置及各点坐标

转向器的输出力矩大小为M，方向由O指向C；直拉杆对转向摇臂的力为大小为F，由点A指向点B，力的作用点为B，此时需要求F的大小。通过F对轴OC的力矩与转向器输出力矩平衡求F的大小。

第一步：通过三维软件，很容易得到各点坐标，如表 1所示：

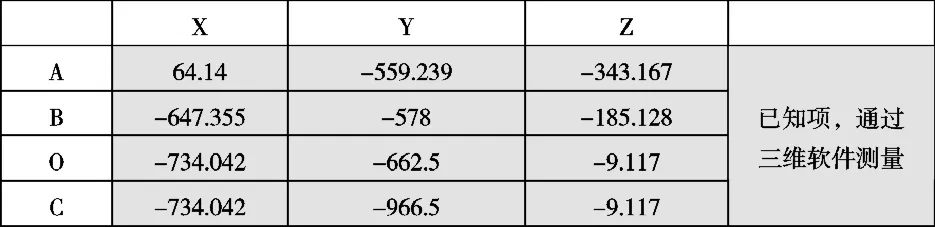
表1 利用三维软件测量各点坐标

第二步：假设AB的长度为力的大小，计算出单位长度在轴OC上产生的力矩大小，如表2。

第三步：根据转向器输出力矩的大小，计算作用在直拉杆上的力的大小，如表3。

3 结论

通过案例表明，向量运算可以将三维软件的空间模拟功能与 EXCEL的运算功能结合在一起，使汽车转向系杆件以及其它机构的受力分析更加准确。

扩展运用：本文中是已知输出力矩求力，如果已知地面作用在轮胎上的力，可以计算出整车的回正力矩、转向阻力矩等，为转向系统的设计及优化提供可靠的依据。

[1] 朱炳麒.理论力学.北京:机械工业出版社,2001.7.

[2] 王望予.汽车设计.北京:机械工业出版社,2004.8.

[3] 江淮汽车集团研发中心.江淮轻型卡车设计规范.第一版,合肥:江淮汽车集团股份有限公司,2006.6.

[4] 百度百科:向量积.