小学数学中“列方程解应用题”的教学启示

刘芳芳

一、小学生在学习列方程解应用题过程中常见的错误

1.解题格式不规范。针对简易方程学习内容的特点，列解方程解应用题的格式跟以前学的算术格式有非常大的区别，学生在学习解方程格式的过程中，会造成各种格式上的错误。有时会漏写“解”；有时等号没有对齐；有时在解完方程后面忘加单位；这些都是学生在初步学习用方程解应用题中最容易出错的细节。

2.假设主体不明确。不管是什么类型的应用题，首先要通读题目，理解题意，找出要求的未知量。例如：同学们参观“远离毒品”展览。四、五年级一共去了264人，五年级去的人数是四年级的1.2倍。两个年级各去了多少人？

解：设两个年级各去了X人。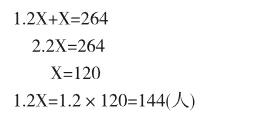

答：四年级去了144人，五年级去了120人。

【错因分析】从解题的过程中，可以很明显看到学生错误的原因是假设的主體不明确，未知量设置错误，学生理所当然地认为求什么设什么，没有深入地审视题目的意思，从而形成思维的混乱，最后造成答题的错误。

3.等量关系不准确。“含有未知数的等式称为方程”，因此“等式”是列方程不可少的条件。相比用算术的方法解决问题，列方程的方法解决问题，则是从设立未知数出发，根据题意把问题表示为含有未知量的等式关系（建立数学模型）。然后利用等式的性质对方程进行恒等变形，求出未知数。

题目：北京故宫占地面积大约72公顷，比天安门广场的2倍少8公顷。天安门广场大约占地多少公顷？

解：设天安门广场大约占地X公顷。

72÷2-8=X

【错因分析】出现此类问题的原因在于部分学生不理解题目的含义，不能正确地找出题目中所蕴含的等量关系，他们往往被题目中的某些词语、短语所吸引，比如说“天安门广场的2倍”、“少8公顷”，学生常常根据自己仅有的简单的数学知识，习惯性地将题目中的语句做出支离破碎的理解：先根据条件“天安门广场的2倍”得到算式“72÷2”，再根据条件“少8公顷”得到算式“72÷2-8”。至于方程中的“=X”，仅是一种可有可无的符号，这就势必导致解答的错误。

二、“列方程解应用题”的错误分析对数学教学的启示

1.拉近数学与生活的距离。一个好的情景创设，往往能引起学生的好奇心和求知欲，有利于引起学生对所发现问题的思考与探究情感，使学生对数学产生亲近感，体验到数学与生活同在。

2.区别列算式与列方程的联系。教师在课堂中必须通过具体的例子，让学生自己试着先用方程来解答，再用算术的方法解决问题，引导学生找出其中差异，如式子的形式及各字母或数字代表的量的不同，使学生渐渐理解用未知量假设为已知量的内涵，切实感受到用方程解题的简便和优越之处，形成将读完题就用方程解题的概念映入脑海中，快速找到题目的切入点，加快解题的速度，让学生从中找到自我效能感，体会到成功的快乐。

3.强化列代数式的练习。教师在引导学生初步形成列列方程解决应用题的思想之后，应利用不同的练习进一步点拨学生掌握分析数量关系的方法和找出等量关系的途径，及时纠正学生错误的解题思维，提高学生解决问题的能力，让学生通过不同的练习明白用方程解决问题的优越性。

4.注重变式思维的发散。教师要鼓励学生从不同的角度寻找等量关系。其次，要让学生初步领会方程的思想，不能就题论题，而应该从方程的视角抓住传统应用题的本质，以实质上具有同类等量关系的问题为主线，突出相应的解法要点，达到触类旁通，体验方程思想和价值的目的。例如，在教学“和倍”问题时，可以以它为切入点，演变为“和差”问题，两个不同的题材，但是它们的解题方法却有共同的地方，从而可以激发学生数学思维。

教师在教学过程中应注重教学策略的改进，避免思维负迁移的影响，强化符号运用和转换训，注重指导学生分析数量关系方法的运用，相信在教师和学生的共同努力下完成有算术解题到方程解题的完美过渡。（作者单位：江西省赣州市蓉江新区潭口镇中心小学）endprint