无粘结预应力活性粉末混凝土梁疲劳性能试验研究

(湖南科技大学 土木工程学院，湖南 湘潭 411201)

活性粉末混凝土(Reactive Powder Concrete，以下称RPC) 是于90年代继高强混凝土之后研制出的具备高强度、高韧性、高耐久性等优良性能的新型水泥基复合材料[1,2]。近年来国内外学者对其开展了大量研究,但大多集中在其静力性能方面[3，4]。然而，如起重机的梁、海上工作台以及公路和铁路桥梁在反复外力实施下，材料内部损伤会不断地积累，最终在不大于静载强度的情况下呈现突然的破坏[5]。为使RPC材料能够在土木领域得到广泛的推广及应用，对RPC材料构成的构件需进行疲劳试验以了解其疲劳性能。本文对4根RPC材料构成的梁施加等幅疲劳荷载，研究RPC梁的性能劣化过程。

1 试验概况

1.1 试验梁基本资料

试验共制造了5根具有相同截面尺寸的RPC梁，1根为普通钢筋RPC梁，另4根为无粘结预应力RPC梁。并根据文献[6]配制普通钢筋，普通钢筋配筋率为3.3%，无粘结预应力梁同时配置1根7股Φs15.2底松弛钢绞线。从4根无粘结预应力RPC梁中选择1根进行静载试验确定疲劳荷载，另3根和普通钢筋RPC梁进行疲劳试验。试验梁配合比见表1，浇筑每根试验梁时同时制作3个100 mm×100 mm×100 mm立方体试块用于测定立方体承担压力的能力，总共制作6个尺寸为100 mm×100 mm×300 mm的棱柱体试块用于测定棱柱体抗压强度及弹性模量。借鉴普通混凝土力学性能试验方法测定RPC材料力学性能，具体试验成果见表2。

表1 RPC配合比水胶比水泥/(kg·m-3)硅灰/(kg·m-3)细砂/(kg·m-3)0 27701931078高效减水剂/(kg·m-3)钢纤维/(kg·m-3)水/(kg·m-3)1977193

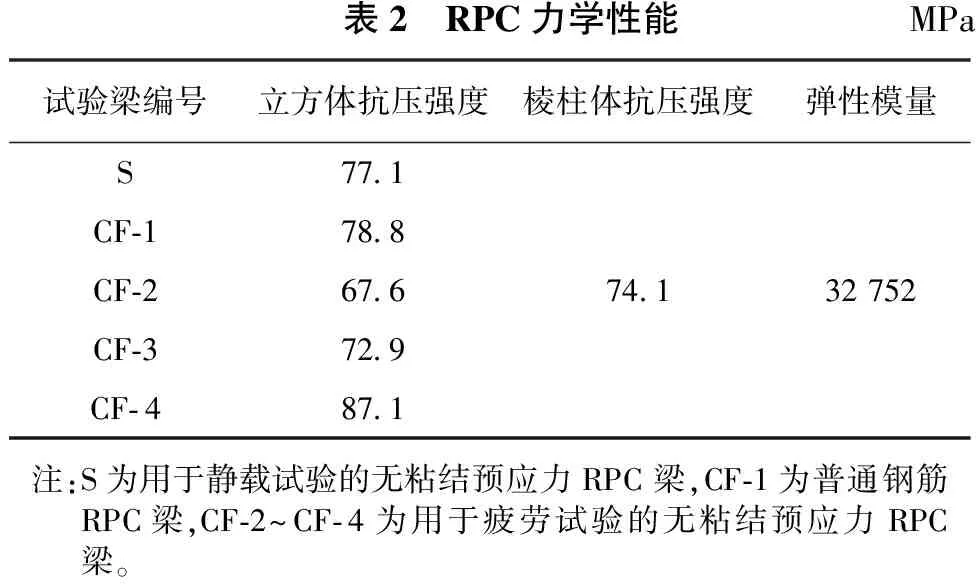
表2 RPC力学性能MPa试验梁编号立方体抗压强度棱柱体抗压强度弹性模量S77 1CF⁃178 8CF⁃267 674 132752CF⁃372 9CF⁃487 1注：S为用于静载试验的无粘结预应力RPC梁，CF⁃1为普通钢筋RPC梁，CF⁃2～CF⁃4为用于疲劳试验的无粘结预应力RPC梁。

1.2 试验加载方案及测点布置

在开展疲劳探究前先进行静态试验，以确定疲劳荷载上限值。疲劳荷载选择出现概率为98%的桥梁疲劳应力幅[5]，上限值为0.3Mu，下限值为0.05Mu。其中Mu为静力试验的极限承载力。静态探究采取三分点加载，疲劳试验运用PMS500型液压脉动疲劳机以4 Hz的频率实行正弦波加载。开始试验前先进行预加力，检测梁体是有没有放稳定，设备能否很好地工作。正式加载过程中当加载次数达到1﹑2﹑1万﹑5万﹑20万﹑50万﹑100万﹑150万和200万次时暂停加载施行一次加卸载的静力试验，同时读取设备读数。

分别在跨中﹑加载点﹑支座位置安放百分表。跨中左右2个面分别张贴5片应变片，普通钢筋在跨中﹑加载点也粘贴应变片。

2 RPC梁静载与疲劳试验结果及分析

2.1 静载试验结果与分析

无粘结预应力RPC梁在静力加载历程中，当外部力加载到75 kN时梁体跨中开始产生竖向裂纹。当加力到270 kN时，跨中位置产生2条急剧拓展的竖向裂纹,此时受拉普通钢筋已经屈服，受压区RPC被压溃。实测的无粘结预应力RPC梁的开裂值Mcr=30.5 kN·m和极限值Mu=108.5 kN·m，开裂弯矩与极限弯矩之比为0.28。高于钢筋混凝土梁0.1的值。无粘结预应力RPC梁表现出较好的耐拉能力，主要是因为掺入钢纤维的RPC材料具有较高的抗拉强度，同时预应力的施加也使得梁的延性及抗裂能的增长。荷载挠度曲线如图1所示，无粘结预应力钢筋应力增量如图2所示。

图1 荷载-挠度曲线

图2 荷载-预应力增量曲线

从上述曲线可以看出无粘结预应力RPC梁在静力实施下，其受力和形变表现为3阶段转变过程：第1过程，在开裂前荷载和挠度基本成线形关系。第2过程，开裂后挠度比荷载增加快但非线性并不是特别明显，主要是因为开裂后RPC中掺入的钢纤维还具有抗拔能力。第3过程，受拉区普通钢筋屈服挠度变化速度加快非线性特性较为明显。

2.2 疲劳试验结果与分析

通过对普通钢筋RPC梁和预应力RPC梁施加荷载幅值为0.25倍静载极限强度的等幅疲劳荷载。在反复外力实施下，不论是普通钢筋RPC梁还是无粘结预应力钢筋RPC梁都能承担200万次的反复外力而不损毁。200万次时RPC梁试验成果与静载试验梁成果对比如表3所示。通过表3呈现出，在200万次反复外力实施后，梁跨中挠度﹑RPC受压区边缘应变﹑受拉区普通钢筋应变﹑预应力增量分别占RPC梁静载极状态时的7%﹑38%﹑26%﹑11%﹑20%，无粘结预应力RPC梁体现了较强的抗疲劳性能。

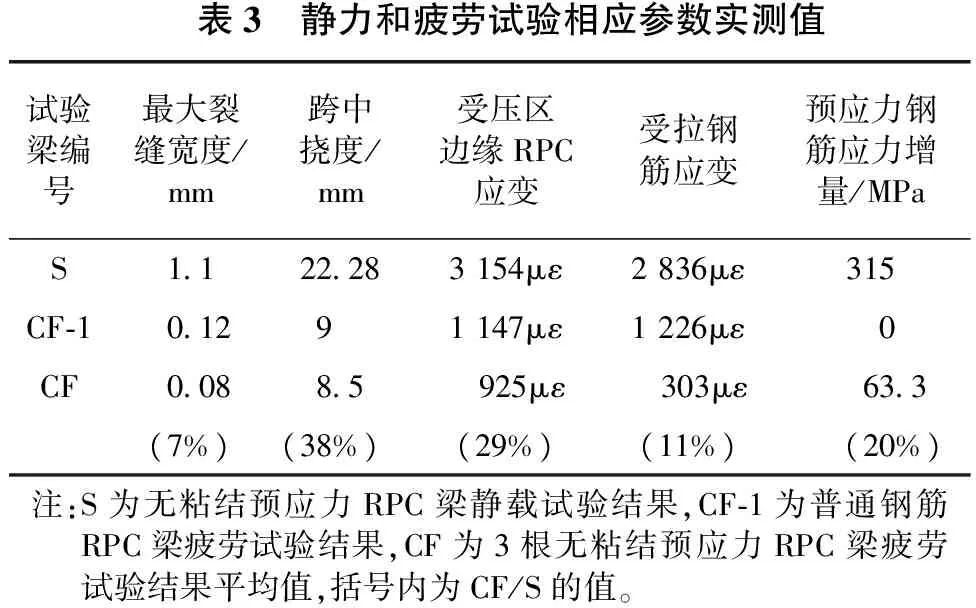
表3 静力和疲劳试验相应参数实测值试验梁编号最大裂缝宽度/mm跨中挠度/mm受压区边缘RPC应变受拉钢筋应变预应力钢筋应力增量/MPaS1 122 283154με2836με315CF⁃10 1291147με1226με0CF0 088 5 925με 303με63 3(7%)(38%)(29%)(11%)(20%)注：S为无粘结预应力RPC梁静载试验结果，CF⁃1为普通钢筋RPC梁疲劳试验结果，CF为3根无粘结预应力RPC梁疲劳试验结果平均值，括号内为CF/S的值。

2.2.1 RPC梁挠度

在试验梁跨中位置安装百分表，利用百分表可以测出挠度随外力循环次数的变化规律，通过挠度的变化可以体现出梁刚度的转变。不同外力循环作用次数下普通钢筋RPC梁及无粘结预应力RPC梁跨中挠度变化曲线如图3、图4所示。不论是普通钢筋RPC梁还是无粘结预应力RPC梁随反复外力实施次数的增加挠度值都不断的增长，并且曲线向挠度坐标轴倾斜，其中无粘结预应力RPC梁挠度倾斜程度比普通钢筋RPC梁倾斜程度大。说明无粘结预应力RPC梁在反复外力下刚度退化比普通钢筋RPC梁刚度退化快。同时疲劳荷载挠度曲线都呈现出先疏后密的特点。

图3 普通钢筋RPC梁跨中挠度随加载次数变化曲线

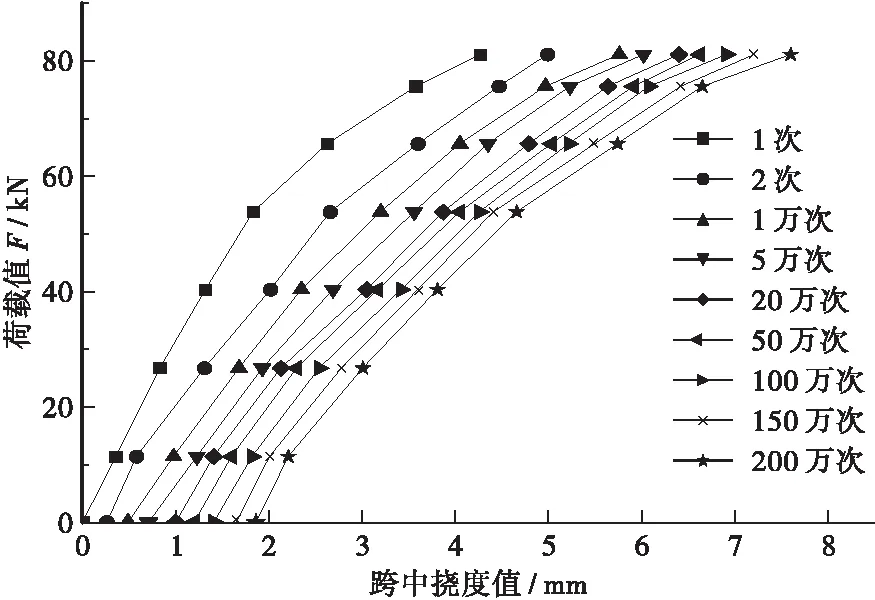
图4 无粘结预应力RPC梁跨中挠度随加载次数变化曲线

2.2.2 受压区边缘RPC应变

等幅疲劳荷载作用下RPC梁受压区应变随外力次数的变化规律如图5、图6所示。图中规律表现为：受压区边缘应变随疲劳加载次数不断增加，相同循环次数作用下无粘结预应力RPC梁受压区边缘应变小于普通钢筋RPC梁。经过200万次加载后，普通钢筋RPC梁边缘压应变为-1 147με，预应力RPC梁边缘压应变为-850με。无粘结预应力RPC梁承压区边缘总应变平均值及累积残余应变平均值随疲劳加载次数的变化规律如图7所示。从图中体现出无粘结预应力RPC梁承压区边缘残余应变和总应变都随疲劳加载次数不停增长，在200万次外力循环过程中表现出两阶段的发展规律：第1阶段结束时疲劳荷载加载次数为23万次，总应变和残余变形分别为662με及115με，该过程总应变和残余应变增长速率较快约占整个过程的11%；第2阶段总变形和残余变形变化速率逐渐减缓，第2阶段末达到200万次循环，总应变为850με,残余应变为262με。第1阶段末总变形和残余应变分别占整个过程的78%和44%，主要因为随着荷载循环次数的增加材料内部的损伤不断地累积导致残余应变在不断地增加。

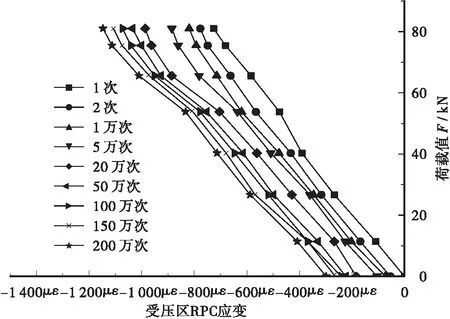
图5 普通钢筋RPC梁边缘应变随加载次数变化曲线

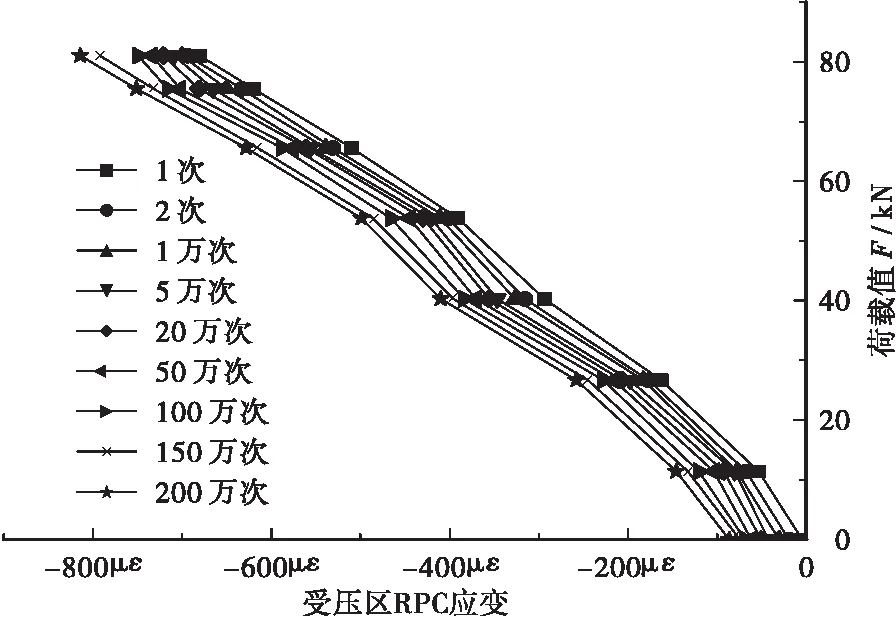
图6 无粘结预应力RPC梁边缘应变随加载次数变化曲线

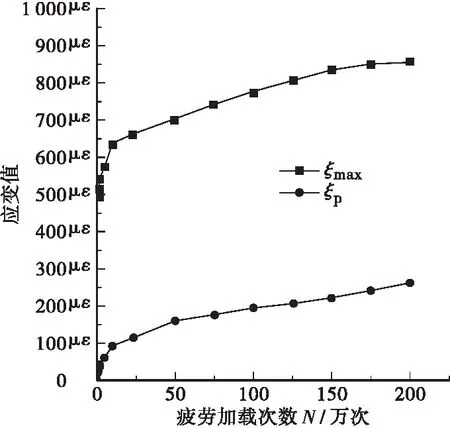
图7 无粘结预应力RPC梁应变随N发展曲线

2.2.3 钢筋应变

对于钢筋的疲劳探究主要通过在空气中实施轴拉试验和对RC梁弯曲加载试验间接测试出钢筋疲劳。首种方式可以加较高的频率值，另一方式更接近实际。图8、图9给出了本次试验过程中普通钢筋应变随加载次数的变化规律。随着反复外力次数的增加2种类型RPC梁中的普通钢筋应变变化速率都在增长。普通钢筋RPC梁加载至53 kN时钢筋应变斜率开始明显变化，而预应力钢筋RPC梁中钢筋应变变化斜率无普通梁中的变化快。同时预应力梁每次加载完后钢筋残余应变不小于普通钢筋梁中钢筋的残余应变。在200万次加载完成后预应力梁中钢筋最大应变约为普通钢筋梁中最大应变的0.5倍。所以对于普通钢筋梁中的钢筋比预应力RPC梁中钢筋更易出现疲劳断裂。

图8 普通钢筋RPC梁钢筋应变变化曲线

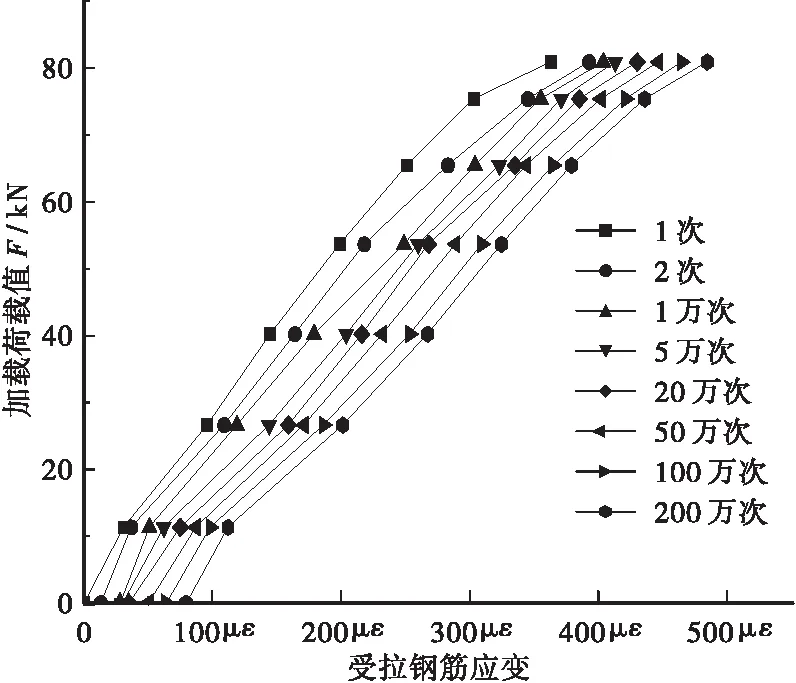
图9 预应力RPC梁钢筋应变变化曲线

3 结论

1)无粘结预应力RPC梁在静态加载过程中表现出了3阶段的规律，第2阶段占整个阶段的60%左右，开裂荷载及极限荷载的比值为0.28。体现出了较强的抗裂能力。

2)在反复外力实施下，无粘结预应力RPC梁的位移变化速率比普通钢筋RPC梁位移变化速率快，说明预应力RPC梁的刚度比普通梁刚度退化快。200万次加载后无粘结预应力梁的挠度值为静力破坏时的28%，表现出较好抗疲劳性。

3)无粘结预应力RPC梁中受压区边缘RPC总应变及残余应变变化体现出两阶段的变化趋势，第1阶段占整个过程的11%，其阶段末总应变及残余应变占整个过程的78%及44%。

4)预应力RPC梁中普通钢筋应变较普通钢筋RPC梁中钢筋应变值小，约为其值的0.5倍，同时应变发展速率也较小，所以预应力RPC梁中普通钢筋抗疲劳性能较在普通钢筋RPC梁中强。

[1] Czarnecki L,Kurdowski W.Tendencje ksztatujаce przyszobetonu[J].Stowarzyszenie Producentów Cementu,2007.

[2] 张明德.RPC混凝土的配制与应用研究[J].福建建材,2010(4):20-23.

[3] 杨胜江.不同养护制度对RPC混凝土力学性能的试验[J].低温建筑技术,2013,35(7):20-22.

[4] 罗许国,刘岱鑫.钢筋活性粉末混凝土梁的疲劳性能试验研究[J].西安建筑科技大学学报(自然科学版),2016,48(4):484-488.

[5] 朱红兵.公路钢筋混凝土简支梁桥疲劳试验与剩余寿命预测方法研究[D].长沙：中南大学,2011.

[6] 郑文忠,李莉,卢姗姗.钢筋活性粉末混凝土简支梁正截面受力性能试验研究[J].建筑结构学报,2011,32(6):125-134.