旋转机械振动信号故障诊断研究

□张 津

上海电气集团股份有限公司 中央研究院 上海 200070

1 研究背景

在冶金、化工、机械等企业中，旋转机械设备约占80%，这些旋转机械设备主要包括发电机、电动机、透平制氧机、鼓风机、大型轧钢机等。在众多的旋转机械故障诊断技术中，没有技术能比振动信号分析更能反映机械设备状况。振动和噪声的强弱及其包含的主要频率成分与故障的类型、程度、部位和原因等有密切联系。当发生故障时，旋转机械的振动信号往往表现为典型的周期性变化。各种机械设备在运行中，都不同程度地存在振动，并且这些振动往往与机器的运行状态相关[1]。

振动信号常包含很多有用的信息，如频率特征、时间特征等。振动信号分析的目的是将信号的某些信息特征通过一定的手段变换为人们容易理解的形式，以便更好地认识信号所代表的物理特性。传统的信号处理方法大多以线性平稳的高斯信号为假设前提，最常用的是傅里叶频谱分析，通过对信号频率域和能量域分布描述来揭示信号频率域的特征，能说明信号中含有哪些频率分量，并且能表示出信号在相应频率处的幅度和相位。实际生活和生产工作中，很多信号是非线性、非平稳的，其统计量是时变的函数，因此需要对振动信号进行更深入的解剖分析，如采用经验模态分解等[2]。

笔者对旋转机械振动信号的故障诊断进行了研究，介绍故障诊断的特征值提取、图谱分析与故障树整理，利用美国SpectraQuest旋转机械故障综合模拟试验台，针对转子不平衡与滚动轴承故障进行模拟仿真，采集信号并进行诊断。

2 故障诊断步骤

旋转机械的故障诊断可以通过特征值提取、图谱分析、故障树整理来完成。其中，振动信号的特征值可以为故障诊断提供判断依据，特征显著的故障完全可以通过一些特征值得出诊断结论。针对多种故障混合或是特征不显著的故障，则需要通过图谱分析提取故障信息，再通过故障树整理来进一步佐证或推导出故障类型[3]。

2.1 特征值提取

特征值主要是用于机械故障的初判定，即判定机械设备是否有故障隐患、程度如何、发展趋势怎样等。特征值主要包括平均值、均方根值、峰值指标、脉冲指标、裕度指标、歪度指标、峭度指标等，指标大小可以表示故障的程度，时间历程曲线可以表示故障的发展趋势。假设采集得到N个振幅为Xi的振动信号，平均值指标为[4]：

均方根值指标为：

均方根值Xrms描述了振动信号的能量，是机械故障诊断系统中用于判定是否存在故障的重要指标。因为均方根值描述振动信号的能量与稳定性，所以当这项指标超出正常值较多时，即可肯定机械存在故障。

峰值指标为：

式中：Xp为振动波形的单峰最大值，通常使用绝对值最大的10个数的算术平均值作为峰值Xp。

脉冲指标为：

脉冲指标Cf和峰值指标Ip都是用来检测信号中是否存在冲击的统计指标。

裕度指标为：

裕度指标Ce通常用于检测机械设备的磨损情况。若裕度指标增大，说明均方根值Xrms比平均值X增大快，说明磨损导致间隙增大。

歪度指标为：

歪度指标Cw反映了振动信号的非对称性。当机械结构存在某一方向的摩擦或碰撞时，会造成振动波性的不对称，歪度指标便会增大。

峭度指标为：

峭度指标Cq反映了振动信号中的冲击特征，正常情况下值约为3。如果值接近4或超过4，则说明机械的运动状况中存在冲击性振动，可能存在间隙过大、滑动副表面破碎等故障。

2.2 图谱分析

单值函数类特征值能够以简单的一个数值来进行判定，因而成为机械故障诊断系统中时域信号特征的主要指标。图谱分析可以进一步提取故障信号的一些频域特征，对多种故障混合或特征不显著的故障进行分解分析。针对不同的故障，图谱分析的方法较多，笔者研究的故障诊断方法包括时域频谱图、轴心轨迹图、瀑布图、时间转速幅值曲线、频谱包络线和经验模态分解[4]。

任何机械振动都具有独立性，振动波在传播过程中相遇会保持各自的振幅、频率、振动方向和传播方向，因此，一个周期信号在某一时刻的幅值可以看作是一系列正、余弦信号在该时刻的幅值之和。机械振动的独立性保证了各个分解信号之间没有干扰，但要在时域内对数目巨大的分解结果进行处理却不切实际。而在频域中，用一个幅值和一个频率唯一表达一个谐波信号，就能避免时域中谐波信号的重叠，将一个可能是不规则的周期信号先规范化，再清晰化，这就形成了振动信号的频谱分析[1]。频谱图作为旋转机械故障诊断的主要手段，可通过观察结果的主频、次频和谐波来推导可能的故障类型。若故障特征不明显，可通过其它图谱进行辅助诊断。

不同时刻下的频谱图组合到一起形成的三维图即为瀑布图，瀑布图以时间为坐标，相比频谱图可更加全面展示旋转机械振动状态的变化，使技术人员了解机械故障的发生与发展过程。旋转机械转动时，在径向平面内的振动轨迹即为轴心轨迹。通过两个相间90°安装的传感器获取波形，绘制成轴心轨迹图曲线，显示随着时间的变化转子在轴承内的振动轨迹，相比单个传感器更能反映机械的状态。频谱包络线是将不同频率的振幅最高点连接起来形成的曲线，对冲击力十分敏感，通常用于诊断轴承或齿轮等低频故障。时间转速幅值曲线针对启停状态下的机械振动，将转速曲线与振动曲线结合分析，能够对比启停机过程中的机械振动时频域，诊断热变形等故障。经验模态分解是一种自适应信号时频处理方法，与傅里叶变换一样，将信号分解为各个相互独立成分的叠加。傅里叶变换有基函数，而经验模态分解假设任何信号都由不同的本征模态函数（IMF）组成，具备自适应性，主要适用于复杂的非线性、非平稳信号。

2.3 故障树整理

进行故障诊断，需要对故障特征进行提取，并代入故障树进行分析，进而得到故障类型。表1为频谱和轴心轨迹图故障树，图1为通过旋转体轴向和径向振动频谱图进行诊断的故障树，图表中1f代表频谱图中1倍频处的振幅，2f代表频谱图中2倍频处的振幅，依次类推。通过两种故障树对应使用，可对基本的故障类型进行判断[5]。

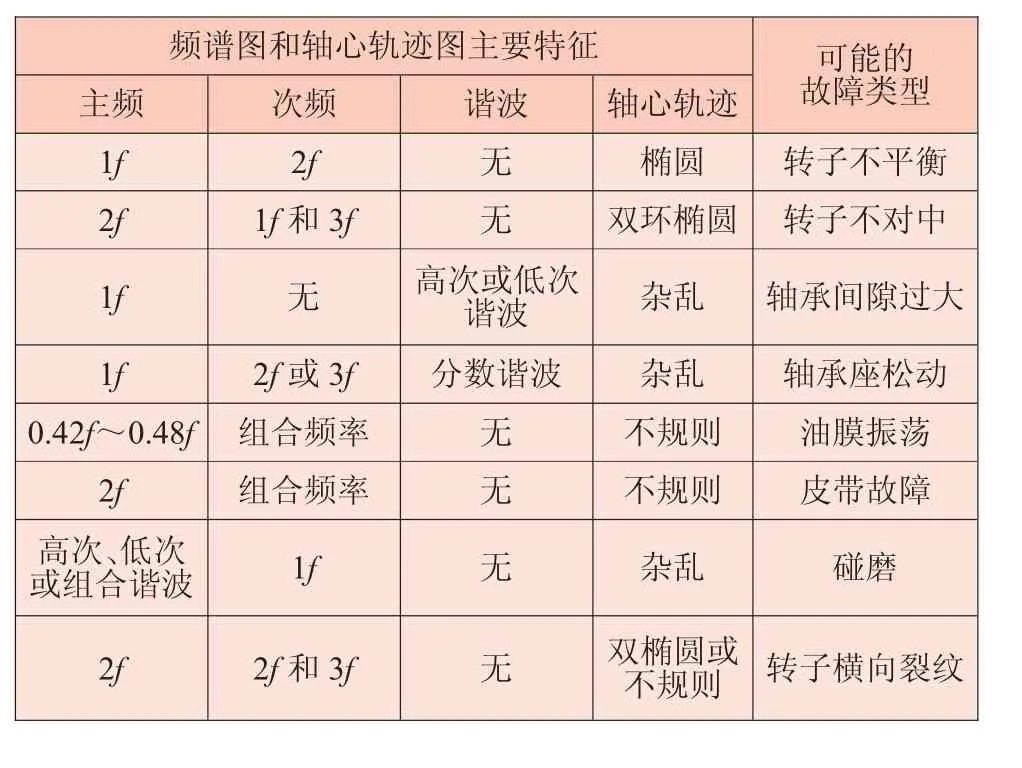
表1 频谱和轴心轨迹图故障树

3 试验结果

使用如图2所示SpectraQuest试验台可以对旋转机械进行常见故障的信号仿真，常见故障包括转子故障、轴承故障、轴心故障、电机故障和摩擦等。

图1 轴向和径向振动频谱图故障树

图2 SpectraQuest试验台

试验使用的试验数据，对应实际工况中最常见与最难判断的两种旋转机械故障，即转子不平衡和滚动轴承故障[6]。匀加速转动，速度由0提升至30 r/s。利用已连接好的加速度传感器和VibraQuest数据采集分析系统，采集振动数据并进行故障诊断[9]。

将所采集的数据导入故障诊断软件进行频谱分析，如图4所示。

3.1 转子不平衡

转子不平衡是由于转子部件质量偏心或出现缺损造成的故障，是旋转机械最常见的振动故障，约占故障总数的80%[7]。不平衡由质量中心与几何中心不重合导致，带来的后果是增加附加载荷，主要表现为1倍频振动幅值随运行时间的延长而逐渐增大。据统计，有50%左右的机械振动是由不平衡力引起的，不正常的机械振动会产生噪声，加速轴承磨损，缩短机械寿命，严重时可造成破坏性事故[8]。因此，对旋转机械转子不平衡故障进行诊断非常重要。

以转子不平衡为例进行试验，不平衡转子如图3所示。在正常平衡转子上加入不平衡螺栓，制成不平衡转子，安装到试验轴上。开启电动机，使电动机

图3 不平衡转子

根据故障诊断软件频谱分析结果可见，振动在30 Hz产生较大振幅，对应转子转速30 r/s，即1倍频。同时，在2倍频处产生较小振幅及部分谐波，根据图谱故障树可见，故障可能由转子不平衡或轴承座松动造成。进一步使用加速度传感器测量轴向和径向振动，导入轴心轨迹图，如图5所示。

由图5可见，振动信号轴心呈椭圆状，因此可以判定旋转机械故障为转子不平衡，即转子偏心。

图4 转子不平衡软件频谱分析截图

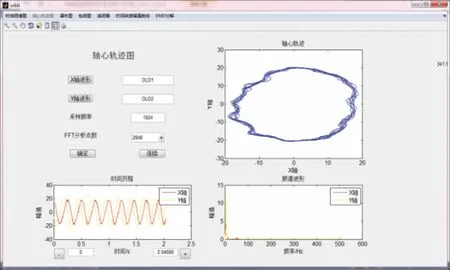
图5 转子不平衡软件轴心轨迹图分析截图

3.2 滚动轴承故障

滚动轴承作为机械设备中重要的旋转零件，也是机械设备的重要故障源之一。滚动轴承故障约占感应电动机故障总数的40%[10]。滚动轴承由内圈、外圈、滚动体、保持架组成，当这4个部分出现磨损剥落等损伤性故障时，便会产生异常振动。因此，要对滚动轴承进行振动诊断，就必须通过频谱分析找出各个部分的故障特征频率，以此来判断滚动轴承的故障位置与严重程度[8]。

由于缺少故障滚动轴承的试验数据，笔者拟用美国凯斯西储大学轴承数据中心提供的故障轴承振动数据进行故障诊断[11]。故障轴承型号为6205-2RS，其基本特征和试验数据见表2，表2中过内圈频率、过外圈频率、保持架频率和滚珠自旋频率为轴承本身的扰动频率。

过内圈频率为：

式中：α为滚珠受力方向与内外滚道垂直线的夹角。

过外圈频率为：

滚珠自旋频率为：

保持架频率为：

表2 6205-2RS轴承基本征与试验数据

设fr为轴承的转动频率，计算滚动轴承各元件故障特征频率[4]。

内圈故障特征频率为：

外圈故障特征频率为：

滚珠故障特征频率为：

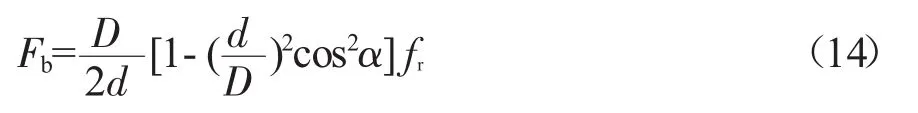
保持架故障特征频率为：

根据上述特征频率公式和相关数据，可计算出轴承的故障特征频率，见表3。

将故障数据导入故障诊断软件，进行频谱分析，如图6所示。结果显示振动存在较多较高的谐波，难以确定故障的特征频率，因此针对这种复杂的非线性、非平稳信号进行经验模态分解。

经验模态分解得到的IMF频谱包络线最终结果如图7所示，可以看到振动的故障特征频率约为157.5 Hz，因此可以判断旋转机械故障位于轴承内圈。

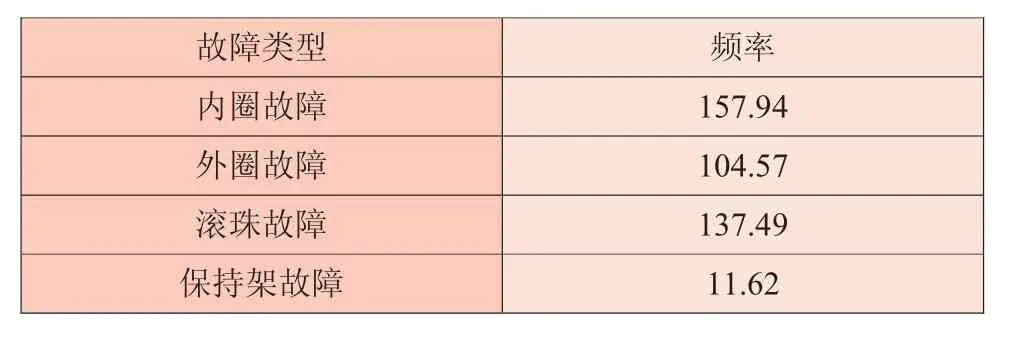
表3 轴承故障特征频率

图6 滚动轴承故障软件频谱分析截图

图7 滚动轴承故障软件经验模态分解截图

4 总结

旋转机械的振动信号故障诊断对保证设备的正常运行具有重要意义，笔者针对旋转机械的振动信号进行了研究，包括频谱分析、轴心轨迹、包络分析、时间转速分析和经验模态分解，并使用旋转机械故障综合模拟试验台对两种典型故障进行仿真试验，通过故障诊断软件进行图谱处理，处理结果由故障树整理进行归纳分析，推导出故障类型。

[1]王垚,蒋东翔,战祥森.旋转机械振动故障诊断知识库的研究与实现[J].汽轮机技术，2003，45（1）：11-13.

[2]朱可恒.滚动轴承振动信号特征提取及诊断方法研究[D].大连：大连理工大学，2013.

[3]朱文博，李郝林，甘屹.故障诊断实例检索方法研究[J].制造业自动化，2011，33（5）：74－77.

[4]高金吉.旋转机械振动故障原因及识别特征研究[J].振动.测试与诊断，1995，15（3）:1-8.

[5]朱文博，刘莎，甘屹.基于案例推理的故障诊断系统软件开发[J].上海电气技术，2010，3（3）：29-33.

[6]杨文涛.旋转机械振动信号特性提取技术研究[D].大庆：东北石油大学，2014.

[7]郭双全.基于灰色关联度的风力发电机组健康性能评估方法研究[J].装备机械，2016（1）：7-11.

[8]苏文胜.滚动轴承振动信号处理及特征提取方法研究[D].大连：大连理工大学，2010.

[9]王浩林，徐志明，甘屹，等.基于网络的数控机床故障预警与诊断平台设计与实现[J].机床与液压，2016，44（11）：181-188，262.

[10]李辉，郭双全，张梦航.基于时间序列的发电机温升趋势分析方法[J].上海电气技术，2016，9（1）：49-58.

[11]朱振军.轴承振动故障分析[J].设备管理与维修，2011（S1）：99-100.