数学思想在高中生物教学中的应用

娄蓝英

摘 要：在学科综合的指导思想下，运用数学学科中的“集合思想、函数思想、计数原理、归纳推理”等数学思想在高中生物教学中的应用研究，有效提高生物课堂的有效性，提高学生的解题能力和解题速度，同时培养学生不同学科知识的迁移能力和综合发展能力。

关键词：数学思想；高中生物教学；应用

数学是学习自然科学的一门基础性和工具性的学科，在高中生物教学中，应对不同的教学内容，教师可以引入不同的“数学思想”帮助学生理解不同的知识，“集合思想”能够让学生更加明确、生动、形象地理解不同的生物学概念以及不同概念之间的联系。把“分类加法计数原理”和“分步乘法计数原理”应用于孟德尔定律，复杂问题简单化，同时培养学生学科之间的迁移能力和综合能力。通过“归纳推理”“函数思想”，拓展学生思维，引导学生从具体的生物现象中建构抽象的数学模型，再用抽象的数学模型来解决具体的生物学现象，使学生能运用数学思维去考虑生物学问题，培养学生分析问题、解决问题的能力。

一、集合思想

在高中数学的学习过程中，集合是一个重要的概念和知识点。一般地，我们把研究对象统称为“元素”，把一些元素组成的总体叫做“集合”，不同的集合之间又存在“子集”“交集”等关系，学生通过这些概念的学习，可以有效地把它运用到高中生物学习中。高中生物教材中有上千个概念，不同的概念之间有区别也有联系，我们可以使用集合之间不同的关系将生物概念分门别类地进行总结和整理，从而帮助学生理解和记忆。

1.子集

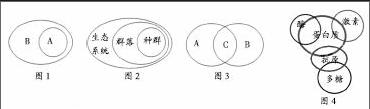
一般地，对于两个集合A、B，如果集合A中任意一个元素都是集合B中的元素，我们就说这两个集合有包含关系，称集合A为集合B的子集，在数学中可用Venn图表示（图1）。

此概念可以用来分析生态学中的“种群”“群落”和“生态系统”等概念，种群指的是占有一定空间和时间的同一物种个体的集合体。也就是说种群作为一个大的集合，其内部的同一物种的生物就是该集合内的“元素”。群落指的是占有一定空间和时间的所有生物种群的集合体，也就是说在群落这个大集合里，所有的种群就是该集合内的“元素”。因此，种群包含于群落中，种群是群落的子集。以此类推，群落在整个自然界的生态系统中也只是其中一个“元素”，群落包含于生态系统中，群落是生态系统的子集。所以可以根据以上关系，“种群”“群落”和“生态系统”三个集合可以画出相应的Venn图（图2）。

2.交集

一般地，由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集，在数学中可用Venn图表示（图3）。在生物学中不同的概念（集合A、集合B）之间有相似点或共同的条件（即交集C），比如：很多物质或结构是植物或动物特有的，但也有些结构是动植物都有的，植物性糖类（集合A）、动物性糖类（集合B）、动植物兼有的糖类（交集C）。有些概念之间比较复杂，用文字表述啰嗦不明，我们就可以借助交集图，比如：蛋白质、抗原、多糖、酶、激素之间的关系（图4）。

二、函数思想

函数是描述事物运动变化规律的数学模型，使用数学语言描述事物就称为数学模型。引导学生从具体的生物现象中建构抽象的数学模型，再用抽象的数学模型来解决具体生物学现象，使学生能运用数学思维去考虑生物学问题，培养学生的学科综合能力和分析、解决问题的能力。

实例：在理想条件下，细菌每20min分裂一次。问题：（1）如果从一个细菌开始，每繁殖一次，细菌数目有多少？（2）根据数据变化规律，用y表示细菌数目，x表示细菌繁殖代数，写出x代后细菌种群数目的表达式？（指数函数y=2x）（3）以时间为横坐标，细菌数目为纵坐标，画出细菌种群数量增长的曲线。结合数学“指数函数”的概念与性质，学生能更好地理解生物知识——“指数增长”。

三、计数原理

在小学时我们已学习了加法和乘法，这是将若干个小的数结合成较大数的最基本技巧，而由他们衍生出来的“分类加法计数原理”和“分步乘法计数原理”是计数问题两个最基本、最重要的方法。《遗传与进化》模块中孟德尔豌豆杂交实验的研究中充分体现和利用了“计数原理”，教师可利用学生已有的数学知识组织教学，让学生亲身体验和感受孟德尔遗传定律的发现过程，培养学生的科学思维和知识应用能力。

1.分类加法计数原理

分类加法计数原理是指完成一件事有两类不同的方案，在第一类方案中有m种不同的方法，在第二类方案中有n种不同的方法，那么完成这件事共有N=m+n种不同的方法。

问题：一对表现型正常的夫婦，有一个患白化病的女儿和正常的儿子。此儿子与一白化病女子婚配，他们生一个正常孩子的概率是多少？

分析：白化病是常染色体隐性遗传，基因设为B、b，则患病女儿为bb，父母均为Bb，正常儿子基因型为BB或Bb，概率分别为1/3，2/3。“此正常儿子与患病女子（bb）婚配，生一个正常孩子的概率”这件事完成有两类情况，第一类为BB1/3×bb→1/3Bb（正常），第二类为2/3Bb×bb→1/3Bb（正常）+1/3bb（患病），那么完成这件事“他们生一个正常孩子的概率”为：1/3Bb（正常）+1/3Bb（正常）=2/3。此类问题，最重要的特征是“或”字的出现。

2.分步乘法计数原理

分类加法计数原理是指完成一件事需要两个步骤，做第一步有m种方法，做第二步有n种方法，那么完成这件事共有N=n×m种不同的方法。孟德尔的自由组合定律涉及两对（或两对以上）等位基因（独立遗传），因此在解答相关题目时，多数学生存在错误率高、解题速度慢的问题，此时我们就可以利用数学中的“分步乘法计数原理”，化难为简。

（1）计算配子的种类

问题：三对等位基因独立遗传（位于三对同源染色体上），则AaBbCc能产生几种配子？

分析：AaBbCc有三对等位基因，所以这件事可以分三步：第一步，Aa能产生2种配子，第二步，Bb能产生2种配子，第三步，Cc能产生2种配子，所以答案是2×2×2=8，AaBbCc总共能产生8种配子。endprint

（2）计算子代基因型、表现型的种类

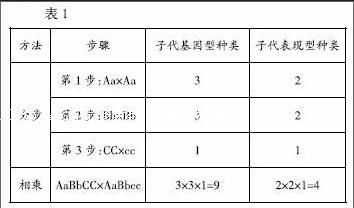
问题：两种基因型亲本杂交（AaBbCC×AaBbcc），子代基因型和表现型分别有几种？

分析：表1

同理我们也可用此方法计算子代基因型、表现型所占比例，如亲本杂交（AaBbCc×AaBbcc），子代中基因型为AaBbcc个体的概率為：1/2×1/2×1/2=1/8，表现型为A_B_cc个体的概率=3/4×3/4×1/2=9/32。

四、归纳推理

由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者由个别事实概括出一般结论的推理，称为归纳推理（简称归纳）。归纳是从部分到整体，从个别到一般的过程，它属于合情推理。

传统上，根据前提所查对象范围的不同，把归纳推理分为完全归纳推理和不完全归纳推理。完全归纳推理考查了某类事物的全部对象，不完全归纳推理则仅仅考查了某类事物的部分对象。自然界的生命现象多种多样，呈现同一生命运动规律的个体往往是无限的，所以在生物学的科学发现中，不完全归纳推理不但是常用的，而且是重要的思维方法。

1.枚举归纳推理

枚举归纳推理是根据某类事物的部分对象具有某种属性，而且没有遇到相反的情况，从而推出这一类事物的全部对象都具有某种属性的归纳推理。枚举归纳推理的结论是或然的，它的可靠程度是和事例数量相关的。

实例：枚举几种氨基酸的结构式，通过观察比较相同点，学生归纳出氨基酸的结构通式：一个中央碳原子上连接着一个氨基、一个羧基、一个氢和一个R基团。此过程遵循了由简单事实到一般规律的数学归纳思想，学生在学习过程中由感性认识上升到理性思维，并通过简单的模型建构，帮助学生理解和记忆核心概念。

2.概率归纳推理

概率归纳推理是以思维对象中的部分对象出现的概率为前提，提出思维对象的全部对象都具有这个概率的结论的推理归纳。高中生物学中的遗传学和生态学，以及实验数据处理中有较多的应用。

实例：孟德尔豌豆7对相对性状的杂交实验和测交实验的子代表现型及比例进行归纳推理（如图5）：（所以前为归纳，所以后为推理）

应用数理统计法处理遗传实验结果，是孟德尔在研究方法上的一大创造，概率归纳推理是“数理统计法处理遗传实验结果”的重要思维方式，由7对相对性状的实验结果到一般的拓展和总结，构成了孟德尔遗传定律的重要基础。

3.科学归纳推理

科学归纳推理不是考查对象数量优势和经验概括，而是以认识事物之间的因果联系为前提，所以，只要能对事物的因果联系作出正确的科学分析，即使数量不多，也能推出可靠的结论。

实例：自然界中的生物成千上万，它们的遗传物质分别是什么？科学家不可能把所有的生物进行科学实验研究，所以我们需要从部分生物的实验研究结论中，找出不同生物之间的差异和联系，归纳推理出所有生物的遗传物质分别是什么（如图6）？（所以前为归纳，所以后为推理）

参考文献：

[1]刘绍学.普通高中课程标准实验教科书数学必修1[M].人民教育出版社，2007：2-9.

[2]刘绍学.普通高中课程标准实验教科书数学选修2-3[M].人民教育出版社，2009：2-4.

[3]刘绍学.普通高中课程标准实验教科书数学选修2-2[M].人民教育出版社，2007：71.endprint