证明一个曲面方程表示柱面的两种有效途径
邓翠容
在《空间解析几何》中,柱面是一种常见且重要的曲面.关于柱面方程的求解分析及几何图形教材中都给了规范的做法.但是反过来,给出一个三元曲面方程,我们要证明它表示一个柱面,这个问题就复杂了,很多学生不会解答这一类题.对此,本文将介绍证明方程表示一个柱面的两种方法,以期帮助大家掌握这个问题.
1 基本定义
由平行于某一定方向且与一条空间定曲线相交的一族平行直线所组成的曲面叫做柱面.定曲线叫做柱面的准线,平行直线族中的每一条都叫做柱面的(直)母线,定方向是直母线的方向,也叫做柱面方向.
2 证明方程表示的曲面为柱面
思路一 构造空间中的一族平行直线,使得它们能够生成这个曲面,这样就证明了该曲面是一个柱面.
思路二 我们将作出一个柱面,它的准线可取为坐标面与题中所给曲面的交线,母线方向设为v→=(X,Y,Z),然后求出这个柱面的方程,再将这个柱面方程与题中所给的方程比较,以确定v→=(X,Y,Z)使两方程一致,这样就证明了题中所给的方程表示的曲面是一个柱面.
下面我们通过两个例题来分别说明这两种方法的应用.
例1 证明方程

表示一个柱面.
证明 将方程(x-z)2+(y+z-a)2=a2改写为

将原方程即(1)式表示的曲面叫做S.
作方程组

其中 λ1,λ2是不全为零的任意实数.对于 λ1∶λ2的每一个值,方程组(2)表示一条直线,因此方程组(2)表示一族直线,称为λ族直线,下面证明λ族直线可以构成整个曲面S,从而该曲面为柱面.为此,需要证明下面两点:
(1)λ族直线中的每一条直线都在曲面S上.
当 λ1λ2≠0 时,将(2)式中的两式相乘得到(1),可见直线(2)在曲面 S 上.当 λ1λ2=0 时,不妨设 λ1=0,λ2≠0,此时(2)变为

显然这条直线也在曲面S上.同理可证得当λ1≠0,λ2=0时相应的直线也在曲面S上.
(2)在曲面S上的每一点处,必有λ族直线中的一条直线经过该点.
设P0(x0,y0,z0)是曲面S上的任意一点,则有

作方程组

这是一个关于λ1,λ2的二元一次齐次方程组,由(3)式知系数行列式等于零,从而上述方程组有非零解,因此可以唯一确定比值λ1∶λ2,于是在λ族直线中有唯一的一条直线经过P0点.
综上可知,曲面S为柱面.
例2 证明方程
2x2+5y2+2z2-2xy-4xz+2yz+2x-10y-2z-1=0表示一个柱面.
分析 这是一个三元二次方程,而且各项都齐全,如果想把它像例1那样,把它改写为一次因子的乘积,再由此写出生成曲面的直线族是比较困难的,为此我们用上面的思路二来解答.
证明 取曲线

即

为准线,母线方向为v→=(X,Y,Z)来建立柱面的方程.
设 P(x,y,z)是柱面上任意一点,则点 P 必定落在某条母线上,即存在准线上一点P1(x1,y1,z1),使得点 P 位于过点 P1且以v→=(X,Y,Z)为方向向量的直线上,于是有

由方程组消去 x1,y1,z1得
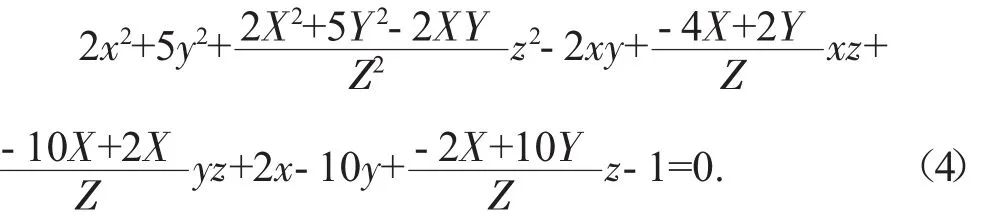
将此式与原方程比较,并取

由此方程得 X∶Y∶Z=1∶0∶1,带入(4)得到的方程即为原方程
2x2+5y2+2z2-2xy-4xz+2yz+2x-10y-2z-1=0,所以原方程表示的曲面是一个以

为准线,母线方向v→=(1,0,1)的柱面.
评注 当方程容易改写为一次因子的乘积时,用例1的方法,计算简单些.当方程不容易改写为一次因子的乘积时,用例2的方法.对于证明方程是柱面的问题,例2的方法是普遍适用的,只是计算量比较大.
[1]李养成.空间解析几何(新版)[M].北京:科学出版社,2008:74-76.
[2]丘维声.解析几何(第二版)[M].北京:北京大学出版社,2007:83-84.

