一类粘弹性流体的多重网格法及其收敛性分析
张宏伟, 邓 燕
1 引言
PTT粘弹流体属于非牛顿流体的范畴,是解决复杂流体动力学中经典且著名的模型之一.像日常生活中的沐浴露、润滑油、表面活性剂等;同时人体的血液、地层内的石油等都是复杂流体.PTT流体模型[1]就是解决此类复杂流体动力学中著名且经典的模型之一.同时此类流体模型问题一直都是有限元研究的一个热点.本文将应用v循环多层网格方法求解一种不考虑扭曲张量的PTT流体流动问题.
2 模型介绍
PTT粘弹流体模型的控制方程为[2]:
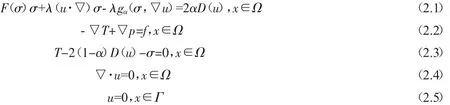
Ω为R2中边界为Γ的多边形区域,σ是粘弹应力张量,它是对称的,T为偏应力张量,u是流速,p是流体压强,f为单位体积力.偏应力张量 T 可分解为弹性部分和粘弹性部分,即 T=2(1-α)D(u)+σ,这里 α(0<α<1)为粘度比常数,D(u)=(▽u+▽uT)/2 是应变率张量.此外,粘弹应力张量 τ需要满足下面的本构方程:-g(ασ,▽u)=2αD(u),其中 λ 是流体的We数,g是双线性泛函,定义如下:
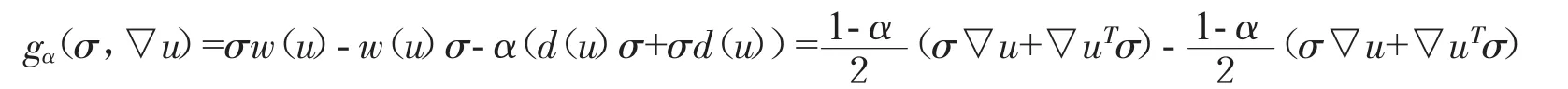
要研究完全的PTT型流体流动问题的数值方法存在很大的困难,因此我们仅研究不考虑扭曲张量的较简单形式的PTT型流体流动问题,即:
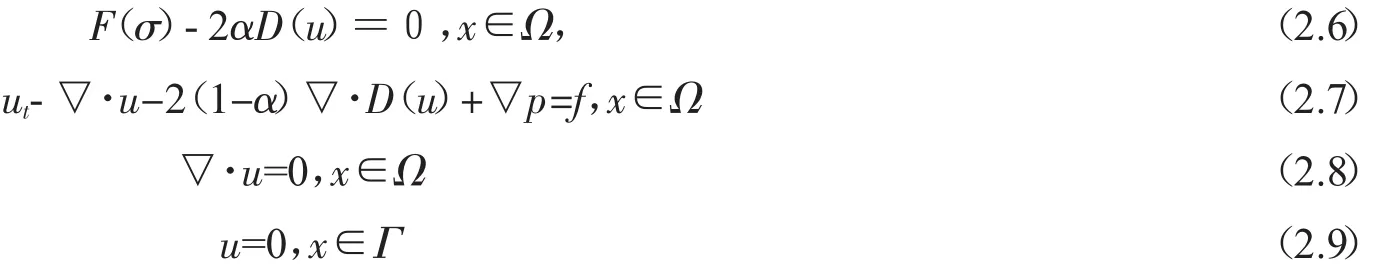
3 PTT流体模型的线性化
假设流体流经的是有界联通的区域Ω⊂Rd(d=2,3),其边界ΓLipschitz连续
假设H(div;Ω)是所有元素和散度都平方可积的向量函数组成的函数空间,即H(div;Ω)={v∈L2(Ω)d∶▽·v∈L2(Ω)}
该函数空间是Hilbert空间,并定义空间中元素的范数如下:
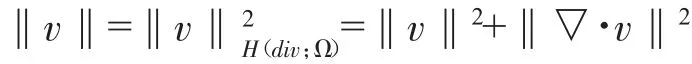
为了将非线性的本构方程进行线性化处理,我们假设粘弹应力张量σ有近似值σ1,即σ≈σ1,并假设该近似值具有如下性质:
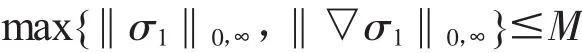
因此有如下近似公式[3]:
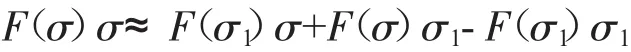
将上述关系式带入PTT流体模型(2.6),可得到如下线性化的PTT模型:

4 PTT粘弹流体流动的v循环多层网格法
下面我们讨论用v循环多层网格法解决PTT粘弹流体的流动问题,具体步骤如下:
步骤一:(前光滑)在细网格Γh2上,对于任意的计算使得它们满足下列方程组:

步骤二:(残量转移)将(4.1-4.3)式与(3.1-3.3)式联合,得到:

然后利用L2投影算子Ql-1将残量转移到粗网格

5 收敛性分析
定理1(存在唯一性):PTT型流体流动的简单形式(3.1-3.3)的v循环多重网格法存在唯一解
类似于文献[4]中的证明.
定理2:设问题(3.1-3.3)的解(σn,un,pn)∈Hk+(1Ω)4×Hk+(2Ω)2×Hk+(1Ω),步骤1的迭代解×Xh2×Qh2,那么对于一直三角剖分Γh2,存在常数C,使得:


我们又令
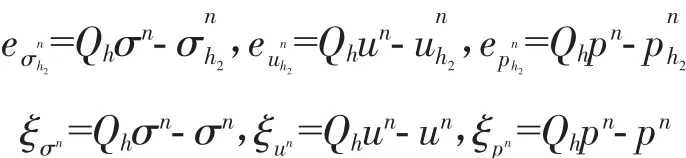
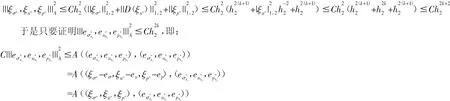

对于上式,利用Poincare不等式,我们有:
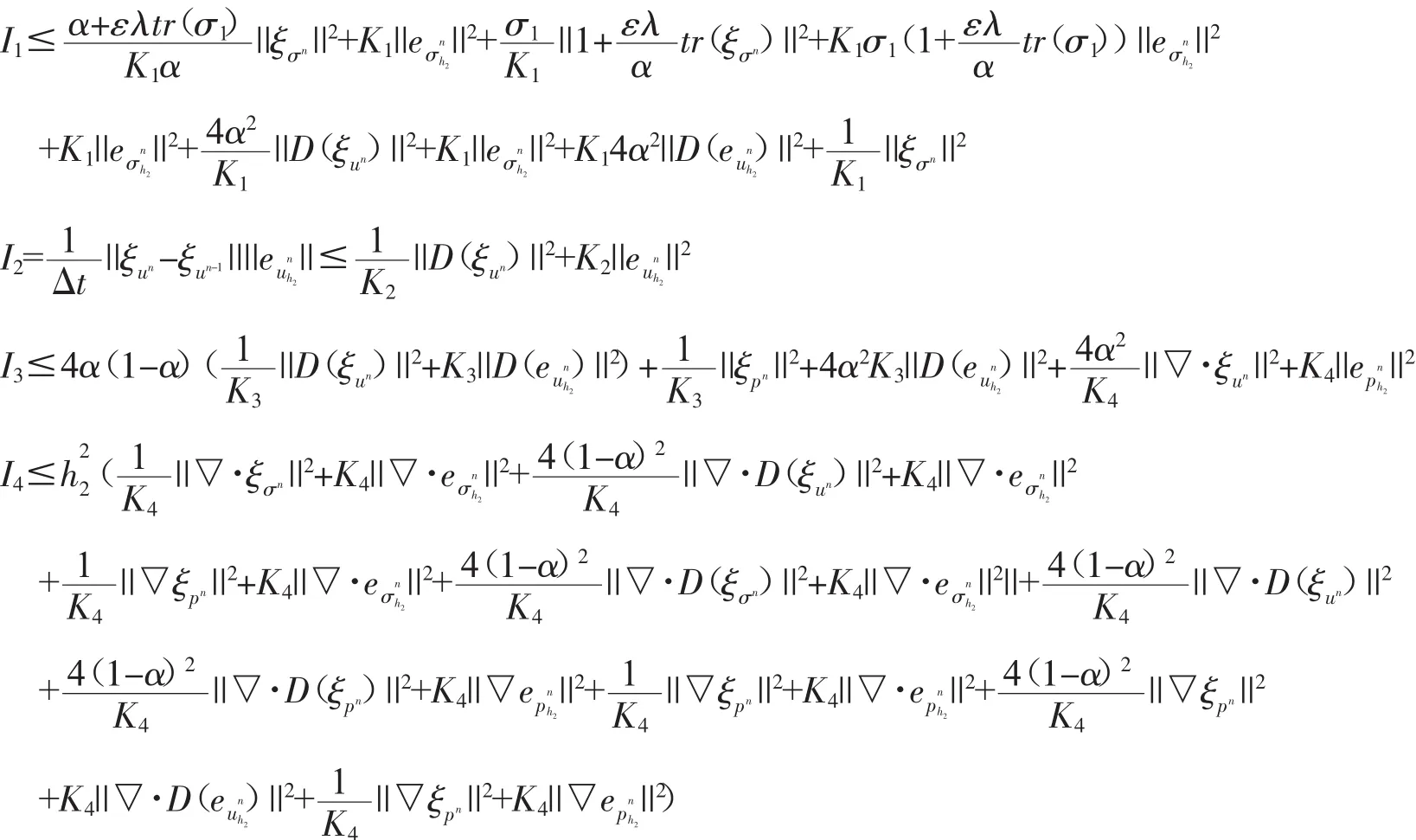
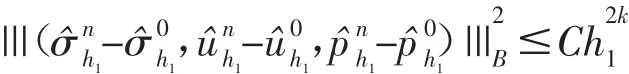
具体推导过程可参考文献[4].
定理4:设问题(3.1-3.3)的解(σn,un,pn)∈Hk+1(Ω)4×Hk+2(Ω)2×Hk+1(Ω)且问题(4.4-4.6)的迭代解),则这时存在与h2无关的正常数C使得v循环多层网格法的迭代解
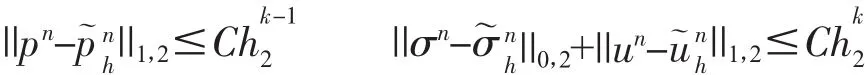
证明:根据定理2,有:

又由相应双线性形式A的范数的定义,可知:
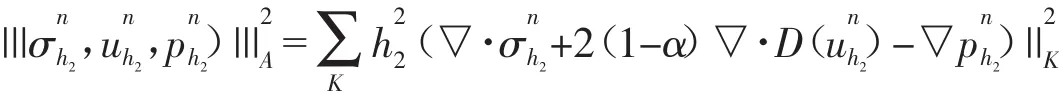
于是我们得到:
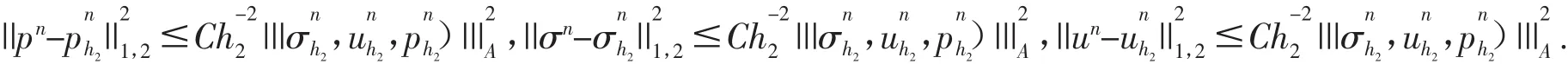
所以,我们有:

利用逼近性质和定理3,我们得到:
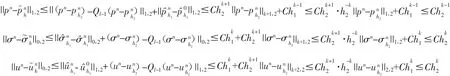
于是定理得证.
[1]王烈衡,许学军.有限元方法的数学基础[M].北京:科学出版社,2004:2-15.
[2]周少玲.非牛顿流体模型的最小二乘有限元方法[M].上海:上海交通大学,2015:12-15.
[3]李开泰,黄艾香,黄庆怀.有限元方法及其应用[M].西安:西安交通大学出版社,1992:12-15.
[4]张宏伟,鲁祖亮,粘弹性流体流动的V循环多层网格法[J].延安大学学报,2007,26(2):15-19.
[5]张宏伟,鲁祖亮,粘弹性流体流动的混合有限元法[J].长沙电力学院学报,2006,21(4):25-28.
[6]鲁祖亮,黄晓.OldroydB型流体的有限元解的存在唯一性[J].湖北名族学院学报(自然科学版),2008,26(1):1-5.

