基于全双工中继网络的功率分配优化策略
,
(太原理工大学 信息工程学院,太原 030024)
0 概述
随着无线通信技术的不断发展,信息安全问题受到了越来越多的关注。基于密码学的传统加密技术被广泛应用[1-3],但是这种加密技术面临着密钥分发困难、密钥可破解等严峻的挑战。物理层安全技术作为对传统加密技术的补充备受关注[4-5]。
为了进一步提高物理层安全网络系统的性能,协作中继技术被提出并广泛得到应用[6]。传统的半双工中继在相互正交的频段进行不同时的信息收发,而全双工中继系统进行同时同频的信息传输。因此,全双工中继系统相比半双工中继系统能够提高接近一倍的频谱效率[7]。但是,全双工中继系统受到来自中继发送天线对于接收天线的自干扰影响。因此,全双工中继系统的应用很大程度上依赖自干扰消除技术的发展[8]。
对于一个通信系统来说,系统能以多大的速率进行安全的信息传输是一个重要的问题。为了衡量系统的安全性能,文献[4-5,9]定义安全容量为最大的安全速率,即主信道和窃听信道的信道速率差的最大值。进一步讲,在系统发送功率有限的情形下研究最大的安全传输速率是一个重要的课题。文献[10]在解码转发中继系统中进行最优的功率分配来达到最大的系统安全速率。文献[11-13]在不同的中继协作方式下进行了最优的功率分配来最大化系统的安全速率。文献[14]研究了双向中继系统的功率分配策略。这些文献都没有研究在自干扰能够有效抑制的情形下全双工中继网络的功率分配问题。
综上所述,本文在自干扰能够有效抑制的情形下,研究在全双工解码转发中继网络中以最大化安全速率为目的的功率优化问题。为解决优化引起的非凸性问题,基于DC规划和凸优化理论提出一种有效的迭代算法。
1 系统模型
如图1所示,系统模型考虑一个源节点S、一个目的节点D、一个中继节点R和一个窃听节点E。除了中继节点具有收发双天线之外,其他节点只具有单天线。

信息传输过程可以在一个时隙完成。首先,源节点S向中继节点R和目的节点D广播信号x。假设此处中继的信号处理时延可以忽略。然后,在中继节点R和目的节点D接收到信号的同时中继节点R解码和重新编码信号为s并且发送出去。最后,目的节点D收到s。在整个传输过程中,窃听节点E能够窃听到来自源节点的x和中继节点的s,中继节点受到残留自干扰的影响。所以,中继节点R、目的节点D以及窃听节点E收到的信号可以分别表示成:
(1)
(2)
(3)

E[|x|2]=1,E[|s|2]=1
根据节点S和D收到的信号以及信号传输速率的定义,主信道的信息传输速率如下:
(4)
从信息论的角度,式(4)表示如果主信道要通信成功,那么发送信息的速率必须同时小于源节点到中继节点以及中继节点到目的节点的信息传输速率,即取两信道的信息速率最小值。
窃听节点E处收到的信号进行最大比率合并(Maximal Ratio Combing,MRC)处理之后,窃听信道的信息传输速率如下:
(5)
系统安全信息速率如下:
Rsec=max{0,min(R1,R2)}
(6)
其中:
(7)
(8)
2 问题公式化
本文主要是在功率受限和系统最小信息安全速率保证的要求下,通过最佳的功率分配来达到最大的信息安全速率。因此,优化问题可以被表示为:
(9)
其中,目的节点和中继节点的功率都有各自限制,根据实际通信的要求,限制条件预设了最小的信息安全速率以保证通信的安全进行。
由式(9)可以看出,目标函数是一个非凸函数,限制条件形成的集合也不是一个凸集。为了解决非凸的优化问题,结合DC规划和凸优化理论,提出了一种有效可行的迭代算法。该算法能够把非凸问题转化成为一系列凸问题,通过凸优化的求解方法可以得到最优解。
3 问题的转化和求解
首先把问题重新写成如下形式:
(10)
由式(10)可知,目标函数被转化为一个线性函数,非凸性被转化到限制条件中。根据DC规划可对公式进行进一步化简。
定理1如果函数A(x)和B(x)都是凸函数,那么问题min{A(x)-B(x),x∈D}就是标准的DC形式,其中,D为凸集。这个问题可以化成如下形式:
min{A(x)-B(xm)-〈B(xm),x-xm〉,x∈D}
(11)
其中,xm为第m次迭代的值,B(xm)为B(x)在xm处的偏导,〈a,b〉代表的是两者的点乘。
式(10)可重新写成如下:
(12)
其中:
已经证明,D(pS,pR)、B(pS,pR)、C(pR)和D(pS,pR)关于pS、pR都是凹函数,则-A(pS,pR)、-B(pS,pR)、-C(pR)和-D(pS,pR)都为凸函数。
利用DC规划,问题可以转化如式(13)所示。
(13)
基于DC规划的迭代算法如下:
步骤1给定所有信道增益、容忍度σ,功率初始值pS(0)和pR(0)。
步骤2利用凸优化方法求出pS(1)和pR(1)。
步骤3计算前后2次求得的功率值对差值直到低于设定的容忍度。
|(pS(m)-pS(m-1))2+(pR(m)-pR(m-1))2|≥σ
步骤4利用凸优化方法求出pS(m+1)和pR(m+1)。
步骤5m=m+1。
步骤6直到收敛。

通过DC规划化简之后的问题是一系列的凸优化问题,可以利用凸优化理论进行凸问题的求解,通过外层基于DC规划的迭代以及内部凸问题的求解,最终会得到最优的功率分配。
4 仿真结果
通过以系统安全速率为指标仿真验证所提的优化方法得到的性能比传统的平均分配策略更优。为了仿真的方便进行,假设所有节点处于同一个水平轴上,假设源节点S、中继节点R、目的节点D以及窃听节点E分别为(0,0)、(100,0)、(200,0)和(300,0),除非有特殊的声明,否则假设不变。仿真参数如表1所示。

表1 仿真参数
在图2中,在窃听者距离dse=300 m的条件下对比了全双工中继网络中最大化安全速率和平均功率2种分配策略中残留自干扰对系统安全速率Rsec的影响。从图2中可看出,随着残留自干扰增益的增大,2种功率分配策略达到的系统安全速率呈下降趋势。这是由于残留自干扰消除不理想的情况下会直接导致合法信道的信道质量降低,进一步会导致合法信道和窃听信道的安全速率差减少,即系统安全速率的降低。另外,以安全速率为衡量目标,本文提出的最大化安全速率策略要优于平均功率分配策略。

图2 残留自干扰信道增益与系统安全速率的关系
在图3中,在残留自干扰相同的条件下,随着总功率Ptot的变化,进行了最大化安全速率和平均功率2种分配策略的性能对比。从图中可以看出,文中提出的功率分配策略的曲线随着总功率Ptot的增大呈上升趋势,而平均功率分配策略的曲线则呈下降趋势。这是由于在发送总功率不断增加的情形下,本文提出的功率分配策略为了实现最大化安全速率的目标会最优地进行功率分配,而平均分配策略在任何情形下都进行平均功率分配,会直接导致安全速率的性能损失。另外,本文也对比了穷举法和提出的迭代算法的性能,可得出文中提出的算法以可容忍的精度损失和低计算复杂度实现了功率的优化分配。
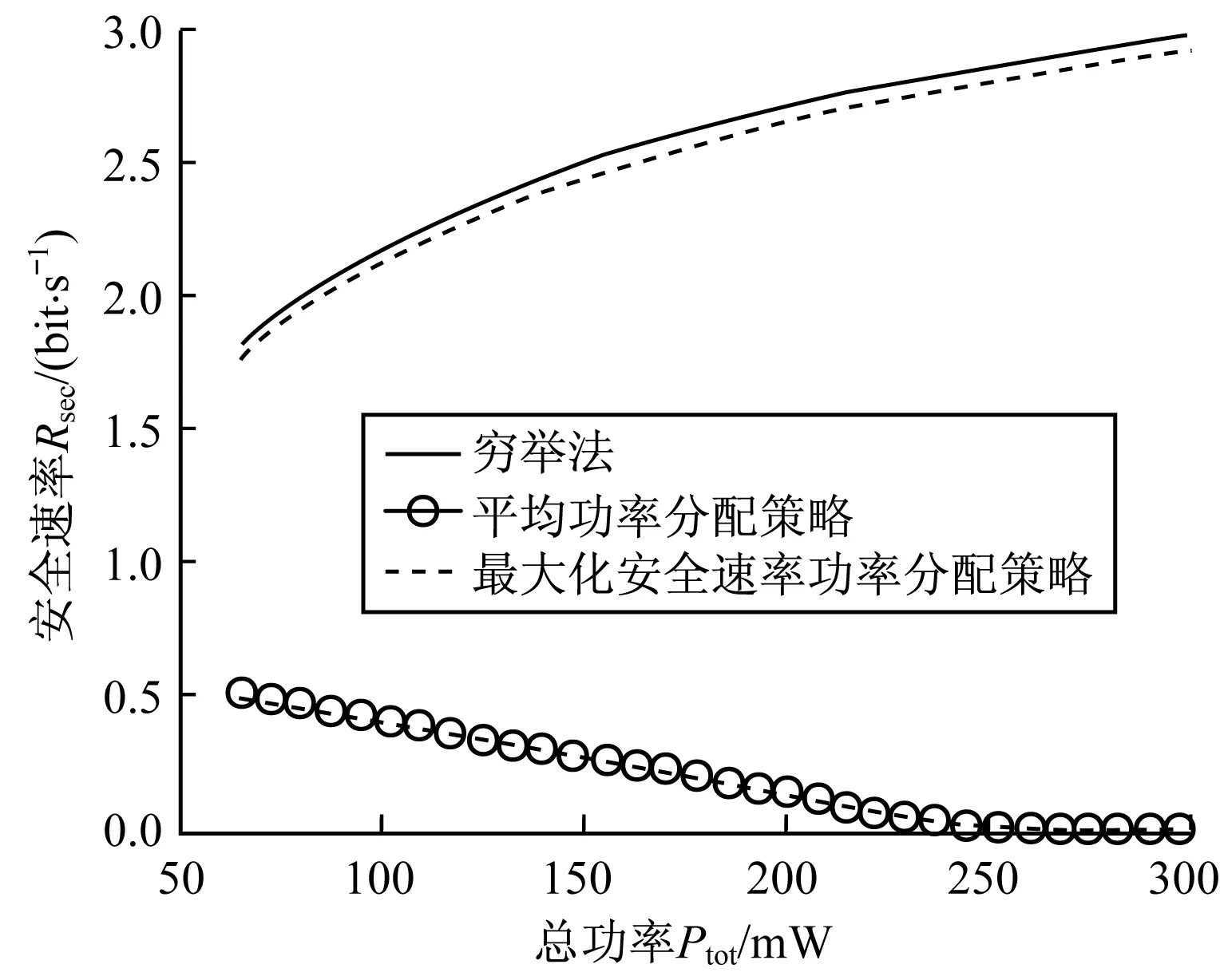
图3 功率分配策略的性能对比1


图4 功率分配策略的性能对比2
在图5中,基于最大化安全速率功率分配策略对比了不同的预设最小的安全速率Rpre对系统安全速率的影响。从图中可看出当预设最小安全速率Rpre增大的时候,Rsec逐渐变小,最后趋于0。从优化问题的限制条件下解释为如果预设安全速率越高,那么对于系统的限制就越大,当达到一定阈值的时候,现有的总功率值在现在的分配策略情况下达不到预设的最小安全速率。总功率值大的曲线会优于总功率值低的曲线。由此得出结论,当预设安全速率越大,表明对系统的要求越高,那么就需要系统投入更大的功率来达到高要求。所以,根据实际情况,一般设置预设最小安全速率不能太高,以此达到安全性和高效能的均衡。
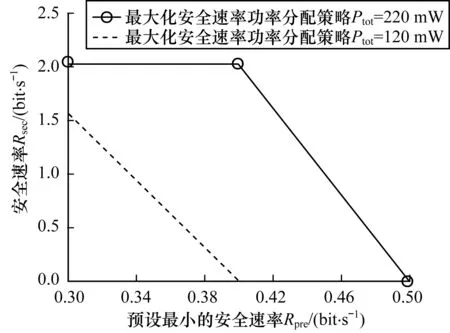
图5 预设最小的安全速率与系统安全速率的关系
5 结束语
本文针对物理层安全的功率分配问题,在全双工解码转发中继协作网络中,基于最大化安全速率的功率分配策略进行最优的功率分配。仿真结果表明,通过与传统平均功率分配策略对比证明了本文研究的功率分配策略能够在实现安全通信的条件下,达到更优的功率分配。但是,本文只研究了简单的通信模型以及理想信道状态下的功率分配策略,实际通信系统设计中往往会面临不理想的信道状态,多中继的选择和多种资源的分配问题,这些优化问题往往具有很高的计算复杂度,因此,下一步将对该问题进行研究。
[1] HELLMAN M E.An Overview of Public Key Crypto-graphy[J].IEEE Communications Magazine,2002,40(5):42-49.
[2] KARTALOPOULOS S V.A Primer on Cryptography in Communications[J].IEEE Communications Magazine,2006,44(4):146-151.
[3] ZOU Yulong.Improving Physical-layer Security in Wireless Communications Using Diversity Techniques[J].IEEE Network,2015,29(1):42-48.
[4] YVO D.Information Theoretic Security[J].Foundations & Trends in Communications & Information Theory,2009,5(4):355-580.
[5] 刘在爽,王 坚,孙 瑞,等.无线通信物理层安全技术综述[J].通信技术,2014,47(2):128-135.
[6] WANG Dong,BAI Bo,CHEN Wei,et al.Energy Efficient Secure Communication over Decode-and-Forward Relay Channels[J].IEEE Transactions on Communications,2015,63(3):892-905.
[7] WANG Li,TIAN Fei,SVENSSON T,et al.Exploiting Full Duplex for Device-to-device Communications in Heterogeneous Networks[J].IEEE Communications Magazine,2015,53(5):146-152.
[8] CHOI D,PARK D.Effective Self Interference Cancellation in Full Duplex Relay Systems[J].Electronics Letters,2012,48(2):129-130.
[9] BARROS J,RODRIGUES M R D.Secrecy Capacity of Wireless Channels[C]//Proceedings of IEEE International Symposium on Information Theory.Washington D.C,USA:IEEE Press,2006:356-360.
[10] JEONG C,KIM I M.Optimal Power Allocation for Secure Multicarrier Relay Systems[J].IEEE Transactions on Signal Processing,2011,59(11):5428-5442.
[11] DONG Lun,HAN Zhu.Improving Wireless Physical Layer Security via Cooperating Relays[J].IEEE Transactions on Signal Processing,2010,58(3):1875-1888.
[12] LI J,PETROPULU A P,WEBER S.On Cooperative Relaying Schemes for Wireless Physical Layer Security[J].IEEE Transactions on Signal Processing,2011,59(10):4985-4997.
[13] YANG Ye,LI Qiang,MA W K,et al.Cooperative Secure Beamforming for AF Relay Networks with Multiple Eavesdroppers[J].IEEE Signal Processing Letters,2013,20(1):35-38.
[14] 曹申好,刘顺兰.双向中继系统的联合中继选择和功率分配策略[J].计算机工程,2013,39(7):127-132.
[15] CHEN Gaojie,GONG Yi,XIAO Pei,et al.Physical Layer Network Security in the Full-Duplex Relay System[J].IEEE Transactions on Information Forensics & Security,2015,10(3):574-583.

