信道预测和联合收发分集的RQAM误符号率性能分析
,,
(杭州电子科技大学 通信工程学院,杭州 310018)
0 概述
具有理想信道状态信息(Channel State Information,CSI)的衰落信道上发射天线选择(Transmit Antenna Selection,TAS)/接收天线最大比合并(Maximal-ratio Combining,MRC)天线分集可获得的分集增益为收、发天线数的乘积,是多入多出无线通信系统中的一种低复杂度的联合收发天线分集方案[1-3]。文献[1-3]研究了在瑞利块衰落信道上TAS/MRC分集下具有理想CSI的二进制相移键控(Binary Phase Shift Keying,BPSK)、M进制相移键控(Multiple Phase Shift Keying,MPSK)和方形M进制正交幅度(Multilevel Quadrature Amplitude Modulation,MQAM)等调制方式的误码性能。文献[4]推导了Nakagami-m衰落信道上TAS/MRC分集下相干检测MPSK、方形MQAM等调制方式的误码性能解析表达式。文献[5]研究了任意相关接收Nakagami-m衰落信道上TAS/MRC下MPSK和方形MQAM的误码性能。文献[6]研究了η-μ衰落信道上TAS/MRC分集下的方形MQAM的误码性能。在实际中,由于无线网络中存在延时以及传输损耗等因素的影响[7],理想的CSI难以获得,其中,信道延时使发射端使用过期的CSI信息,导致系统误码性能恶化。文献[8]研究在瑞利块衰落信道上反馈延时对TAS/MRC分集下的BPSK误码性能的影响。文献[9]研究了在存在反馈延时的时间选择性瑞利块衰落信道上TAS/MRC分集下的BPSK和四相相移键控(Quadri Phase Shift Keying,QPSK)调制的误码性能。文献[10]推导了存在反馈延时的Nakagami-m衰落信道上TAS/MRC分集下MPSK、方形MQAM的误码性能解析表达式。利用导频符号辅助调制(Pilot Symbol Assisted Modulation,PSAM)技术可以获得CSI信息,文献[11]将单入单出衰落信道上的PSAM技术扩展到多入多出系统[12]。文献[13-14]将PSAM技术和信道预测应用于TAS/MRC分集系统(即TASP/MRC)以克服反馈延时引起的系统误码性能恶化,并推导时间选择性瑞利块衰落信道上采用PSAM技术和最小均方误差(Minimun Mean Square Error,MMSE)维纳滤波器的BPSK调制误码性能。矩形正交幅度调制(Rectangular Quadrature Amplitude Modulation,RQAM)具有频谱利用率高、实现简单的特点[15],方形MQAM和差分编码四相相移键控(Diferentially-encoded Quadriphase Shift Keying,DE-QPSK)是其特殊情况,在高速无线通信系统中获得广泛应用[16]。为此,本文分别推导在时间选择性瑞利块衰落信道上采用MMSE维纳信道预测器和TAS/MRC天线分集的RQAM、DE-QPSK的平均误符号率(Average Symbol Error Rate,ASER)精确和近似表达式,并对其进行仿真。
1 系统模型
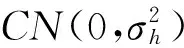
(1)
其中,τ=DLbTs为信道延时,Ts为RQAM或DE-QPSK的符号周期,D为正整数,fd为多普勒频移,E[.]表示求期望,J0(.)是第一类零阶Bessel函数[14]。
假定使用文献[13-14]的PSAM技术和N阶MMSE维纳信道预测器来完成对信道估计和预测,由维纳-霍夫方程可得到前D个数据块的信道增益预测值为[14]:
(2)
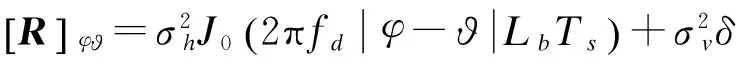
(3)
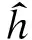
TASP/MRC接收机合并器输出信噪比(SNR)γ的概率密度函数为[14]:
(4)
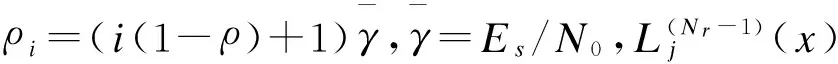
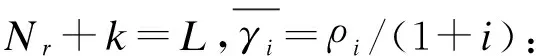
(5)
(6)
利用文献[14]的拉盖尔多项式展开式:
(7)
将式(7)代入式(4)中,利用式(5)、式(6)经化简可得γ的概率密度函数为:
(8)
于是经推导可得γ的矩生成函数(Moment Generating Function,MGF)为:
(9)
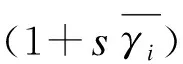
2 精确性能分析
在时间选择性瑞利块衰落信道上采用TASP/ MRC和MMSE维纳信道预测器的RQAM和DE- QPSK的ASER,可由其在AWGN下的条件误符号率Ps(e|γ)对fγmax(γ)求统计平均后得到[18],即:
(10)
下面利用MGF法和高斯Q函数的另一种表达式推导时间选择性瑞利块衰落信道上采用MMSE维纳信道预测器和TASP/MRC天线分集的RQAM、DE-QPSK的ASER的精确表达式。
2.1 RQAM
在AWGN信道上采用相干检测的矩形MI×MQQAM的条件误符号率为[15,18]:
(11)
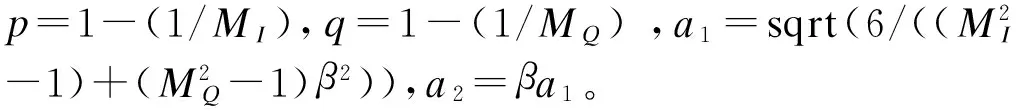
利用文献[18]中Q(x)和Q(x)Q(y)的另外一种表达式:
(12)
(13)
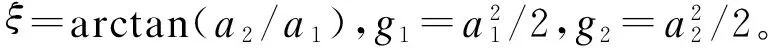
将式(8)和式(11)~式(13)代入式(10)中,可得瑞利块衰落信道上采用TASP/MRC和MMSE维纳信道预测器的矩形MI×MQQAM的ASER为:
Ps=2pI1+2qI2-4pqI3
(14)
式中:
(15)
(16)
令z=cos2θ,经计算可得:
(17)
其中,2F1(a,b;c;x)为高斯超几何函数[19-20]。
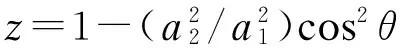

(18)
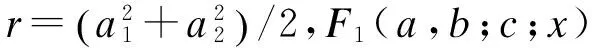
将式(15)~式(18)代入式(14)可得瑞利块衰落信道上采用TASP/MRC和MMSE信道预测器的矩形MI×MQQAM的ASER为:
(19)
2.2 DE-QPSK
在AWGN信道上相干解调DE-QPSK的条件误符号率为[16,18]:
(20)
将式(8)、式(20)代入式(10)可得瑞利块衰落信道上采用TASP/MRC和MMSE维纳信道预测器的DE-QPSK的ASER为:
(21)
其中:
(22)
令z=cos2θ,并利用文献[18]中的(5.18a)可推得:
(23)
利用文献[20]的式(6.1.39):
(24)
并将其代入式(23)中,有:
(25)
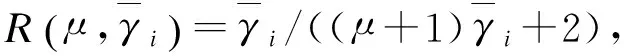
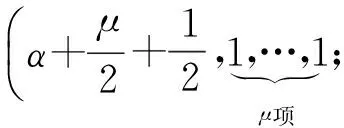
m≥2
(26)
将式(25)、式(26)代入式(21)中,可得瑞利块衰落信道上采用TASP/MRC和MMSE维纳信道预测器的DE-QPSK的ASER为:
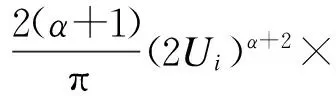
(27)
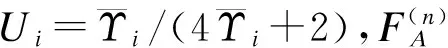
3 近似性能分析
为了简化计算,利用MGF法和高斯Q函数近似表达式,推导时间选择性瑞利块衰落信道上采用MMSE维纳信道预测器和TAS/MRC天线分集的RQAM、DE-QPSK的ASER近似表达式。
3.1 RQAM
根据文献[18],高斯Q函数的近似为:
(28)
其中,w1=0.301 7,w2=0.438 9,w3=1.051 0,t=1,2。
将式(8)、式(11)、式(28)代入式(10),可得采用TASP/MRC和MMSE维纳信道预测器的矩形MI×MQQAM的近似ASER为:
P≈2pY1+2qY2-4pqY3
(29)
其中:
(30)
(31)
(32)
利用式(9)和式(30)~式(32)经推导得:
(33)
(34)
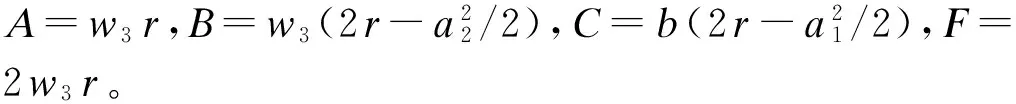
将式(33)、式(34)代入式(29)中,得到瑞利块衰落信道上采用TASP/MRC和MMSE维纳信道预测器的RQAM的近似ASER为:
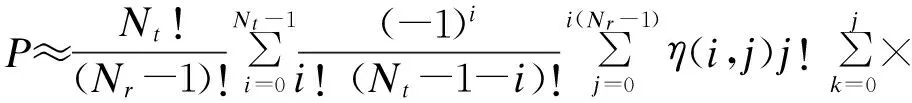
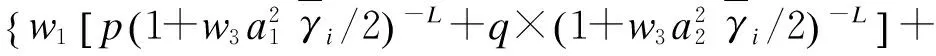
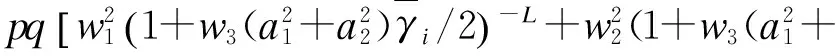
(35)
3.2 DE-QPSK
将式(8)、式(20)、式(28)代入式(10)中可得瑞利块衰落信道上采用TASP/MRC和MMSE维纳信道预测器的DE-QPSK的近似ASER为:
P≈4Z1-8Z2+8Z3-4Z4
(36)
利用式(28),采用与式(30)~式(32)相类似的推导方法可得:
(37)
(38)
(39)

(40)
利用式(9)和式(37)~式(40)经推导可得:
(41)
(42)
(43)
(44)
将式(41)~式(44)代入式(36),并将w1,w2,w3的值代入式(36)中,得到瑞利块衰落信道上采用TASP/MRC和MMSE维纳信道预测器的DE-QPSK的ASER近似表达式为:
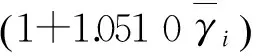
(45)
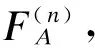
4 数值计算与仿真
下面假定所有收发天线上的多普勒频移均相同,采用与文献[14]相同的信道参数,即Ts=10-6、Ep/N0=30 dB、fd=100 Hz、Lb=1/(100fdTs),以采用DE- QPSK或矩形4×2QAM(dI=dQ)调制的(Nt,1;Nr)的TASP/MRC系统为例,对不同的归一化延时fdτ下时间选择性瑞利块衰落信道上采用MMSE维纳信道预测器的TASP/MRC的DE-QPSK和矩形4×2QAM进行数值计算和Matlab仿真,结果如图1~图5所示,其中时间选择性瑞利块衰落信道采用文献[18]中的方法产生,图1~图4为在预测阶数L=5情况下的仿真结果。
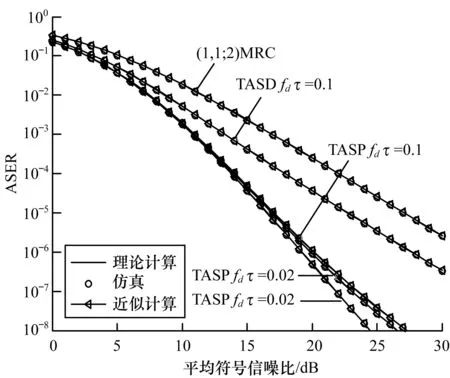
图1 不同fdτ下DE-QPSK的精确和近似ASER性能
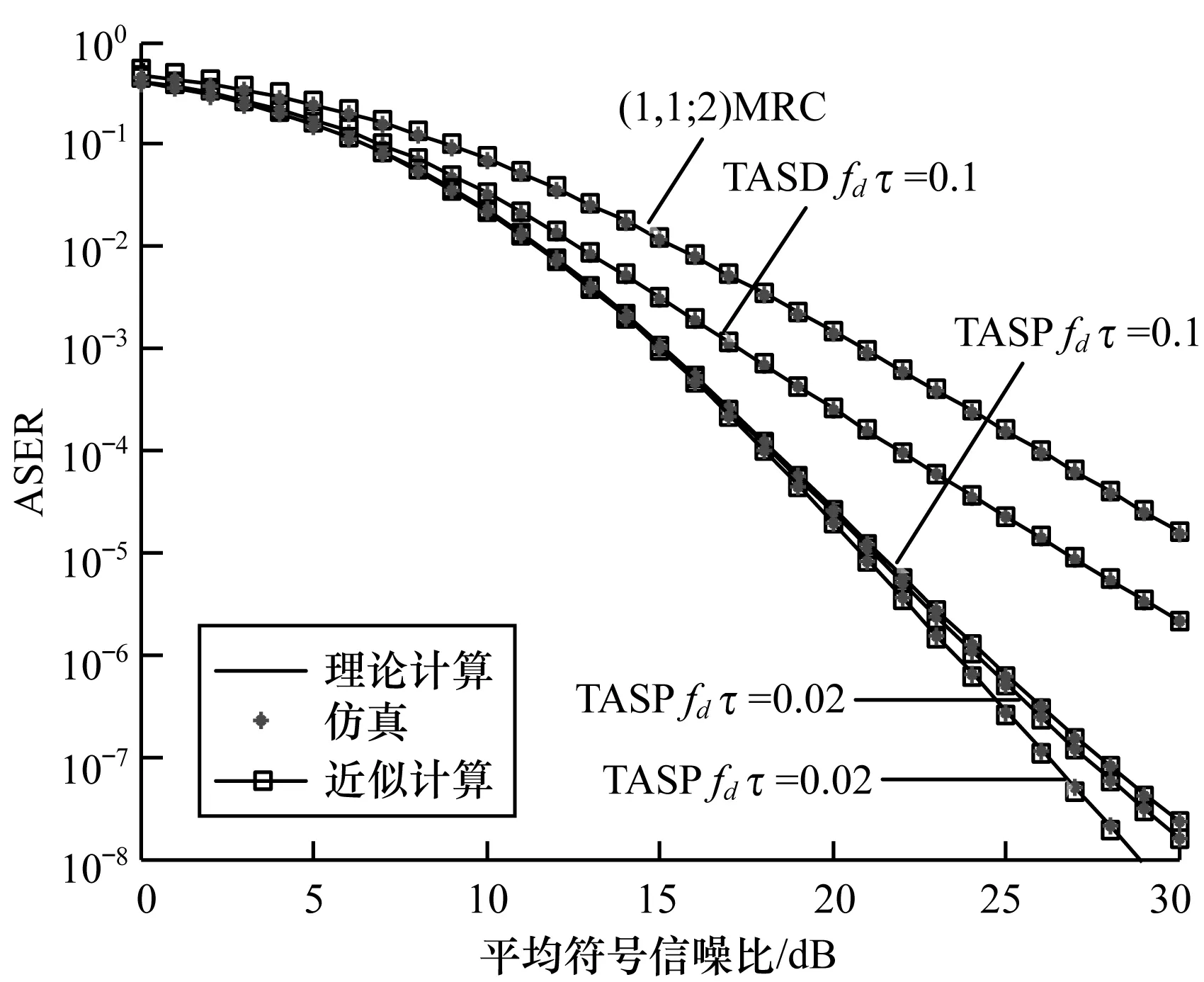
图2 不同fdτ下4×2QAM的精确和近似ASER性能
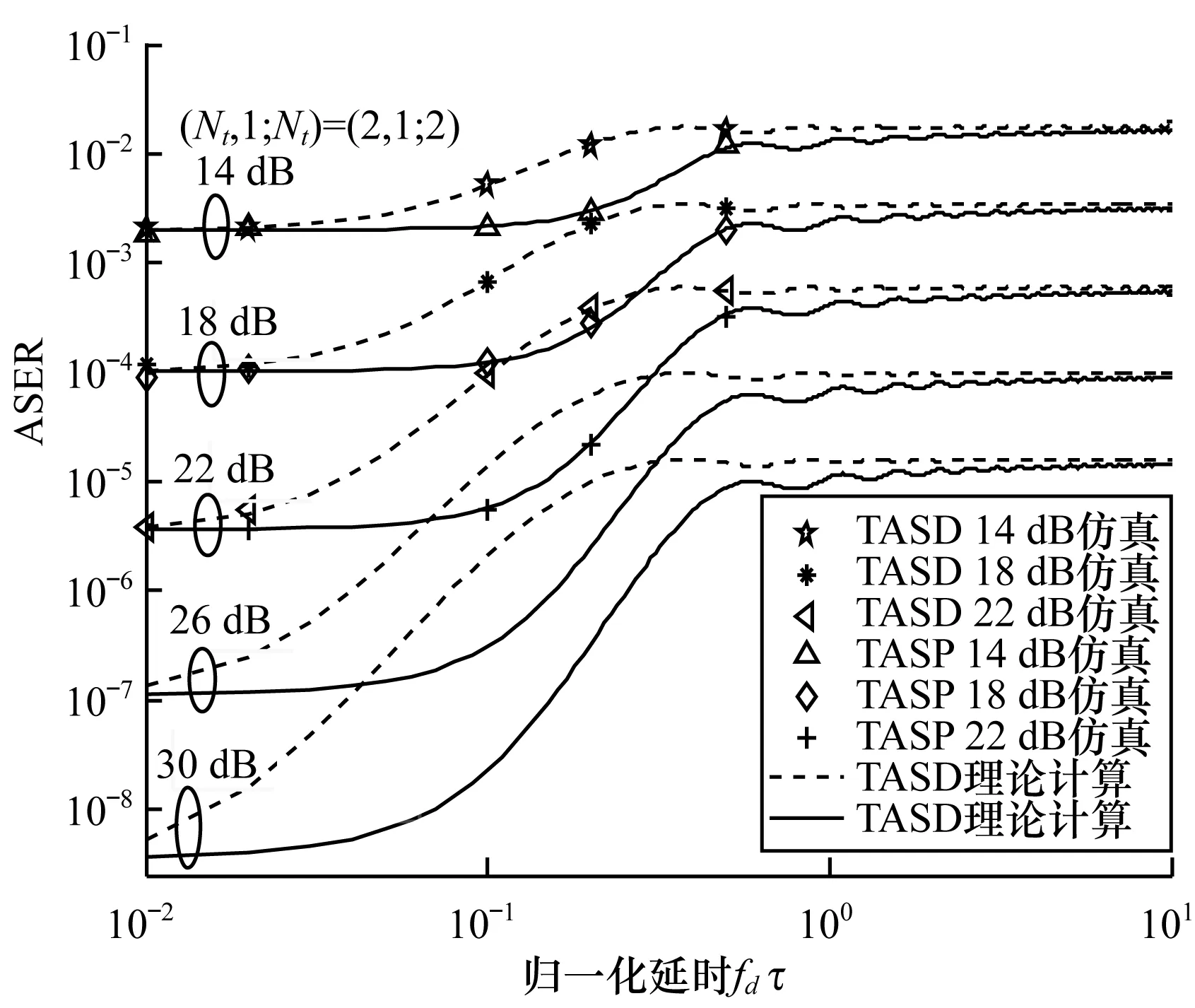
图3 不同下4×2QAM的精确和近似ASER曲线
图1和图2分别给出了时间选择性瑞利块衰落信道上和TASP/MRC天线分集的不同归一化延时fdτ下采用MMSE信道预测器的DE-QPSK和4×2QAM的 ASER性能曲线,并与文献[14]中的反馈延时发射天线选择/接收MRC(TASD/ MRC)天线分集方案进行比较。
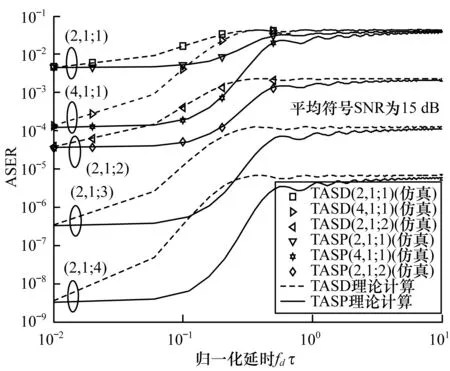
图4 不同(Nt,1;Nr)下DE-QPSK的ASER性能曲线
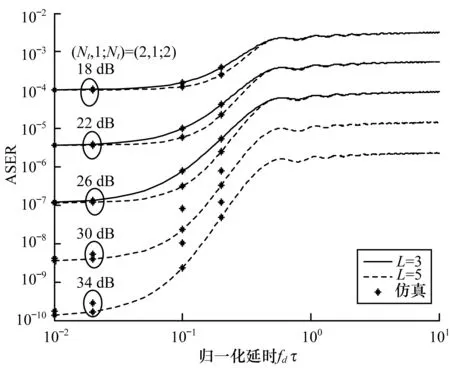
图5 不同L和下4×2QAM调制的ASER性能
由图1和图2可知,在小信噪比和小延时下TASD/MRC和TASP/MRC的ASER性能几乎相同。归一化延时fdτ越大,采用TASP/MRC的ASER性能改善越明显。如ASER=10-6时,采用TASP/MRC较采用TASD/MRC的DE-QPSK、4×2 QAM在归一化延时fdτ=0.02和0.1时分别有1.2 dB和7.5 dB、1.8 dB和8 dB的信噪比性能改善。在大归一化延时fdτ情况下,采用TASD/MRC的DE-QPSK和4×2QAM调制信号的ASER与开环(1,1;2)MRC的ASER性能相近,TASP/MRC的ASER性能明显优于TASD/MRC。
由图1~图5可以看出,DE-QPSK和4×2QAM的ASER近似值和精确值非常接近、精确值和仿真值吻合,从而验证了近似分析的准确性和理论分析的正确性。
5 结束语
本文利用MGF方法和高斯Q的另一种表达式或近似表达式,分别推导了时间选择性瑞利块衰落信道上采用MMSE维纳信道预测器和TAS/MRC天线分集的ASER精确和近似表达式,理论结果与仿真结果都证明了矩形QAM和DE-QPSK调制的ASER性能近似分析的准确性和理论分析的正确性,可见,本文的结果为时间选择性瑞利块衰落信道上采用MMSE维纳预测器和存在信道反馈延时的TASP/MRC系统设计提供一种理论分析工具。
[1] 李光球.相关衰落信道上MIMO系统中组合SC/MRC的性能分析[J].电波科学学报,2009,24(1):163-166.
[2] 李光球,曹晓波.瑞利衰落信道采用组合发射机SC/接收机MRC的MQAM性能分析[J].电子学报,2003,31 (7):1080- 1082.
[3] CHEN Z,YUAN J,VUCETIC B.Analysis of Transmit Antenna Selection/Maximal-ratio Combining in Rayleigh Fading Channels[J].IEEE Transactions on Vehicular Technology,2005,54(4):1312-1321.
[4] 李光球.Nakagami衰落信道上组合SC/MRC的性能分析[J].电波科学学报,2007,22(2):187-190,250.
[6] KUMBHANI B,KSHETRIMAYUM R S.Analysis of TAS/MRC Based MIMO Systems overη-μFading Channels[J].IETE Technical Review,2015,32(4):252-259.
[7] 李长乐,李建东,蔡雪莲,等.无线局域网有效支持智能天线应用的接入时延性能分析[J].计算机学报,2006,42(1):37-44.
[8] PRAKASH S,MCLOUGHLIN I.Channel Prediction for Mitigating Feedback Link Issues in Transmit Antenna Selection Systems[C]//Proceedings of International Symposium on Personal,Indoor and Mobile Radio Communications.Tokyo,Japan:[s.n.],2009:973-977.
[9] ONGGOSANUSI E N,GATHERER A,DABAK A G.Performance Analysis of Closed-loop Transmit Diversity in the Presence of Feed-back Delay[J].IEEE Transactions on Communications,2001,49(9):1618-1630.
[10] RADAYDEH R M.Receive Maximal-ratio Combining with Outdated Arbitrary Transmit Antenna Selection in Nakagami-M Fading[J].IET Communications,2009,10(3):1638-1648.
[11] CAVERS J K.An Analysis of Pilot Symbol Assisted Modulation for Rayleigh Fading Channels[J].IEEE Transactions on Vehicular Technology,1991,40(4):686-693.
[12] PRAKASH S,MCLOUGHLIN I.Predictive Transmit Antenna Selection with Maximal Ratio Combining[C]//Proceedings of Global Telecommunications Conference.Honolulu,USA:[s.n.],2009:1-6.
[13] 田心记,李晓静.MIMO干扰信道中改进的干扰消除方法[J].计算机工程,2016,42(10):135-139.
[14] PRAKASH S,MCLOUGHLIN I.Effects of Channel Prediction for Transmit Antenna Selection with Maximal-ratio Combining in Rayleigh Fading[J].IEEE Transactions on Vehicular Technology,2011,60(6):2555-2568.
[15] MAAREF A,AÏSSA S.Exact Error Probability Analysis of Rectangular QAM for Single and Multichannel Reception in Nakagami-M Fading Channels[J].IEEE Transactions on Communications,2009,57(1):214-221.
[16] RADAYDEH R M,MATALGAH M.Results for Infinite Integrals Involving Higher-order Powers of the Gaussian Q-function with Application to Average SEP Analysis of DE-QPSK[J].IEEE Transactions on Wireless Communications,2008,7(3):793-798.
[17] 叶新荣,张爱清,麻金继.一种仿真瑞利信道的有效方法[J].中国科学院研究生院学报,2010,27(2):228-233.
[18] SIMON M K,ALOUINI M S.Digital Communication over Fading Channels[M].New York,USA:John Wiley & Sons Inc.,2005.
[19] SHI Q,KARASAWA Y.Some Applications of Lauricella Hypergeometric Function F_A in Performance Analysis of Wireless Communications[J].IEEE Communications Letters,2012,16(5):581-584.
[20] ABRAMOWITZ M.Handbook of Mathematical Functions:With Formulas,Graphs,and Mathematical Tables[M].[S.l.]:US Government Printing Office,1967.

