复杂曲面的三坐标测量机采样参数选取

陈大伟，陈岳坪，杨 翊，周晓慧

（1.广西科技大学 机械工程学院，广西 柳州 545006；2.柳州市特种设备检验所，广西 柳州 545006）

1 引言

随着现代制造业的快速发展，人们对零部件的轮廓构造提出了多元化的要求，具有复杂型面的零部件越来越多地得到了应用，检测技术的地位也随之日益凸显。因此，对复杂型面的高效率、高精度的测量及评定的要求也越来越高[1]。三坐标测量机在检测零件时主要使用触发式测头和扫描测头，离散数据的获得方式是通过测量一系列离散点，并把这些测点的坐标作为测量结果。

最精确的方法测量曲面，得到的结果也存在误差。测量精度与测量工具、测量环境、测量方法等因素有关，可以对某些因素进行合理优化，保证测量结果的准确性。文献[2]研究了测点采样间隔和测球直径对测量结果的影响。文献[3]研究了三坐标测量机采点数目和采点方法对测量误差的影响。同一个零件表面由无数个点组成，三坐标测量机却只能测量离散的点集，所以，文献[4-5]认为曲面测量误差与测点的位置和数目有关。文献[4]还认为空间自曲面在三坐标测量误差与测量区域、网格尺寸和测球直径有关。相关文献表明，复杂曲面三坐标测量的形状误差与测球形状和测球直径有关。如文献[6-7]表明，改变球头直径的大小，可能会导致轮廓不同程度的变形，并且将会改变微观高度的值。在采样间隔方面，一方面，如果采样间隔太小，曲面需要通过大量数据来表示，这将降低测量效率；另一方面，如果取样间隔过大时，可能无法测量到曲率半径较小位置的关键点，将会影响到测量精度。因此，选择采样参数应根据测球直径来进行[7]。

2 采样参数

采样策略包括了采样间隔和测球直径等，其应受到被测要素的实际状况（误差精度和体量）、测量系统精度、测量评定要求等方面的影响[8]。考虑三坐标测量机的超高精度，因此忽略测量系统的测点误差的因素，重点研究采样间隔和测球直径的两个关键采样参数对测量结果的影响。

2.1 采样间隔选择

采样间隔是指测球相邻两次采样时间的测量点之间的距离，如图1所示，可以看出，采样间隔越小，复杂曲面上的测点数将会布置越多，更有效反映曲面的实际轮廓。文献[9-10]认为测球直径与采样间隔，最常用的比例为0.5：1、1：1和2：1，主要参考上述采样原则进行实验，确定最合理的采样参数。

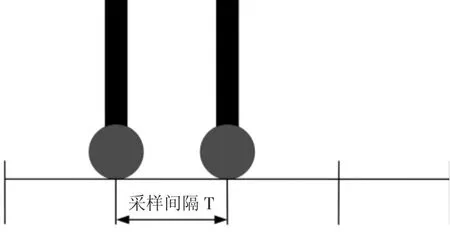
图1 采样间隔T示意图Fig.1 Sampling Interval T

2.2 测球直径选择

测球直径多为（0.3～8）mm，为了测量复杂曲面零件的各个部位，测球测量曲面示意图，如图2所示。可以看出，测球位于轮廓波谷处，测球直径越小，更易接近轮廓实际位置，保证测量结果的准确性，所以尽量选择直径较小的测球。同时，尽可能的选择较短的测针，否则测针越长其弯曲或变形量越大，精度越低。实验分别使用直径为1.5mm，5mm，8mm的三种测球，对复杂曲面进行测量，并对实验结果进行分析与总结。

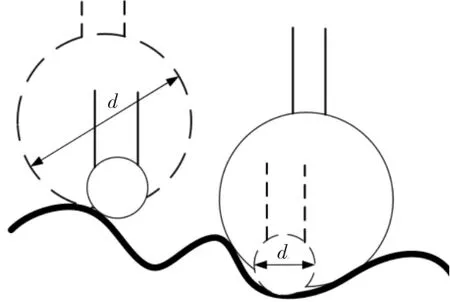
图2 测球测量曲面示意图Fig.2 Measuring Surface of Measuring Ball

3 实验研究

为了研究不同采样参数对三坐标测量误差的影响，采用了一实例零件进行实验验证。零件是一个B样条曲面，数控加工是在一个标准长度为80mm80mm17mm铝合金毛坯进行，精加工使用球头铣刀直径为8mm，主轴转速为3000r/min，进给率为500 mm/min，走刀方式为行切法，行距为0.4 mm，加工后的实物，如图3所示。曲面测量实验在德国海克斯康Leitz Reference HP三坐标测量机（Quindos软件，MPEE=0.9+L/400μm）下进行，配备接触触发式测头，测球直径为1.5mm，3mm，5mm，8mm测针各一根。实验内容主要包括：（a）曲线在接触式测量时，在同一球头直径采用三种不同的采样间隔；（b）在同一采样间隔采用三种不同测球直径；（c）曲面接触式测量选用两种不同参数组合。

3.1 采样间隔影响

曲线是在B样条曲面上相截得到，截面是（y=40，2.5≤x≤77.5），得到曲线，如图4所示。选择测球直径，在方向分别选择100，50，20个测点进行测量实验，每组测点等间距分布，整个曲线在每个测点法向偏差，如图5所示。从图5可以看出，在100个测量点的情况下，测球直径与采样间隔的比为2：1时，轮廓上相邻测点之间的距离最短，相比50个测点（）与20个测点（）测量法向偏差要大，结果，如表1所示。可以看出，测点数目多的平均值、最大值、最大轮廓高度要比测点数目少要大。因此要想提高复杂曲面测量精度，尽可能在曲面上选择更多的测量点。

图3 曲面实物图Fig.3 Material Object of Surface

图4 曲线位置图Fig.4 Location of Curve

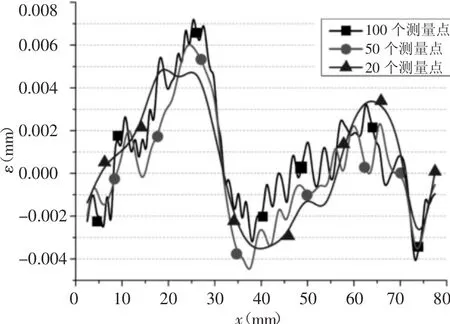
图5 不同数目测量点的曲线法向偏差Fig.5 Normal Deviations of Curve for Different Numbers of Measurement Points

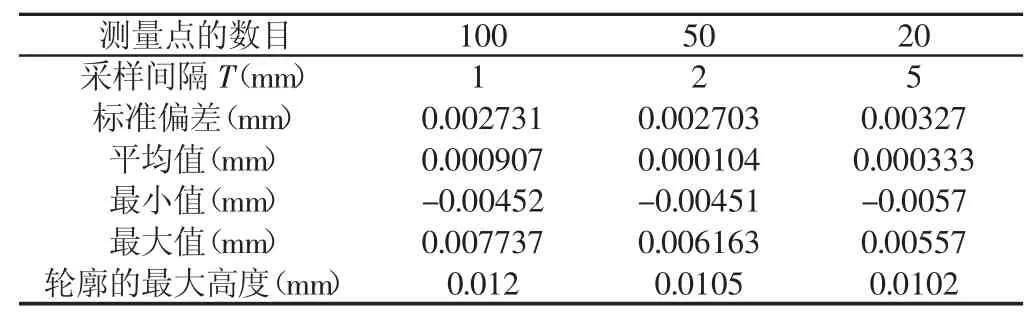
表1 不同采样间隔的法向偏差Tab.1 Normal Deviations of Different Sampling Intervals

3.2 测球直径的影响

分别采用测球直径为1.5mm，5mm，8mm的三根测针对复杂曲线进行采点，每次采点数为100个，曲线，如图4所示。在三种球头直径下测得曲线法向偏差，如图6所示。测量结果，如表2所示。

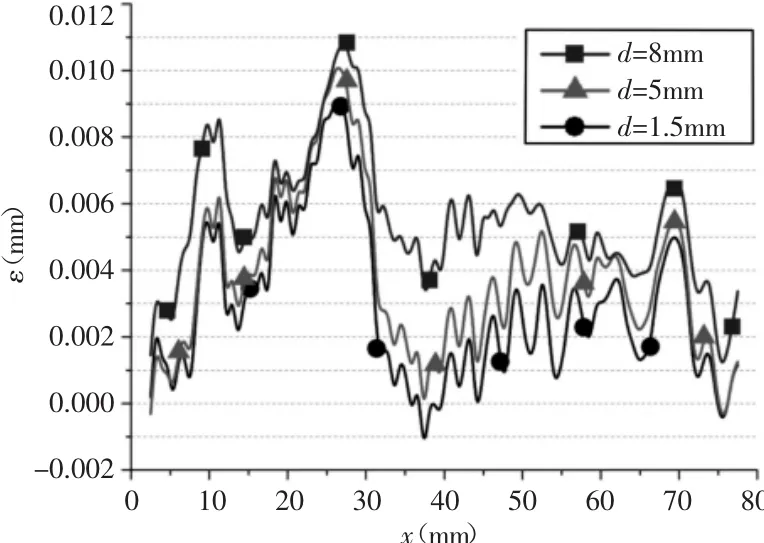
图6 不同测球直径的曲线法向偏差Fig.6 Normal Deviations of Curve for Different Diameter of Measuring Ball

从图6可以看出，使用的测球要比、更容易测得复杂曲线轮廓的波谷，反映轮廓更真实形状，曲面测量误差更小。从表2得出，测球直径为1.5mm测得轮廓最大高度要比测球轮廓度要大0.0011mm。因此在复杂曲面测量时尽可能的使用较小直径的测球，减小曲面轮廓在法向的测量误差，提高曲面的测量精度。

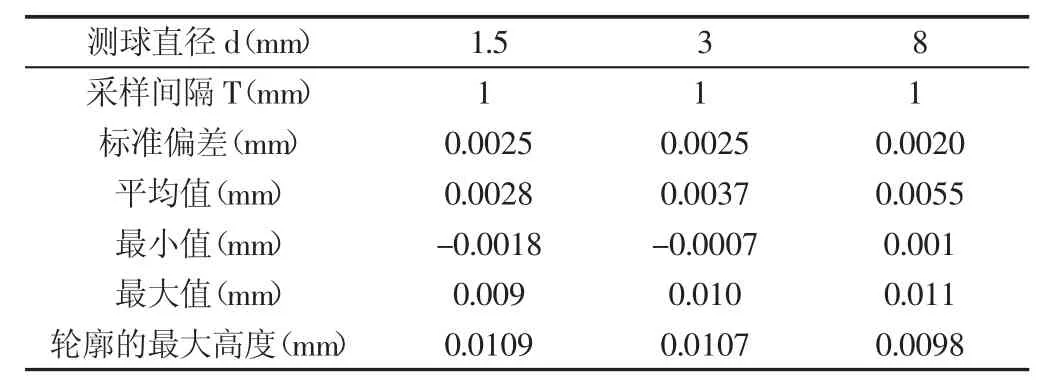
表2 不同测球直径的曲线法向偏差Tab.2 Curve Normal Deviations of Different Diameter of Measuring Ball

3.3 两组参数组合的影响

实验测量B样条曲面的区域为，第一种实验方法使用球头直径为1.5mm在曲面布置6400个测点（80行×80列，样本间隔为0.75mm），另外一种实验方法使用球头直径为5mm在曲面布置576个测点（24行×24列，样本间隔为2.5mm），实验结果，如图7和表3所示。该组实验是在的采样原则下，研究测球直径和采样间隔对复杂曲面法向偏差的影响。对比图7中的a，b可以看出，使用测球直径比测球直径测得曲面法向偏差要大。在采样间隔较大情况下，复杂曲面曲率半径小的坐标数据易被忽略，进而降低了曲面的测量精度。由表3可以看出，同时采用较小的测球直径与采样间隔，所得的平均值、最小值和轮廓最大高度相对较大。因此，尽可能选择直径较小的测球，以及较小的采样间隔，来提高复杂曲面三坐标测量的精度。

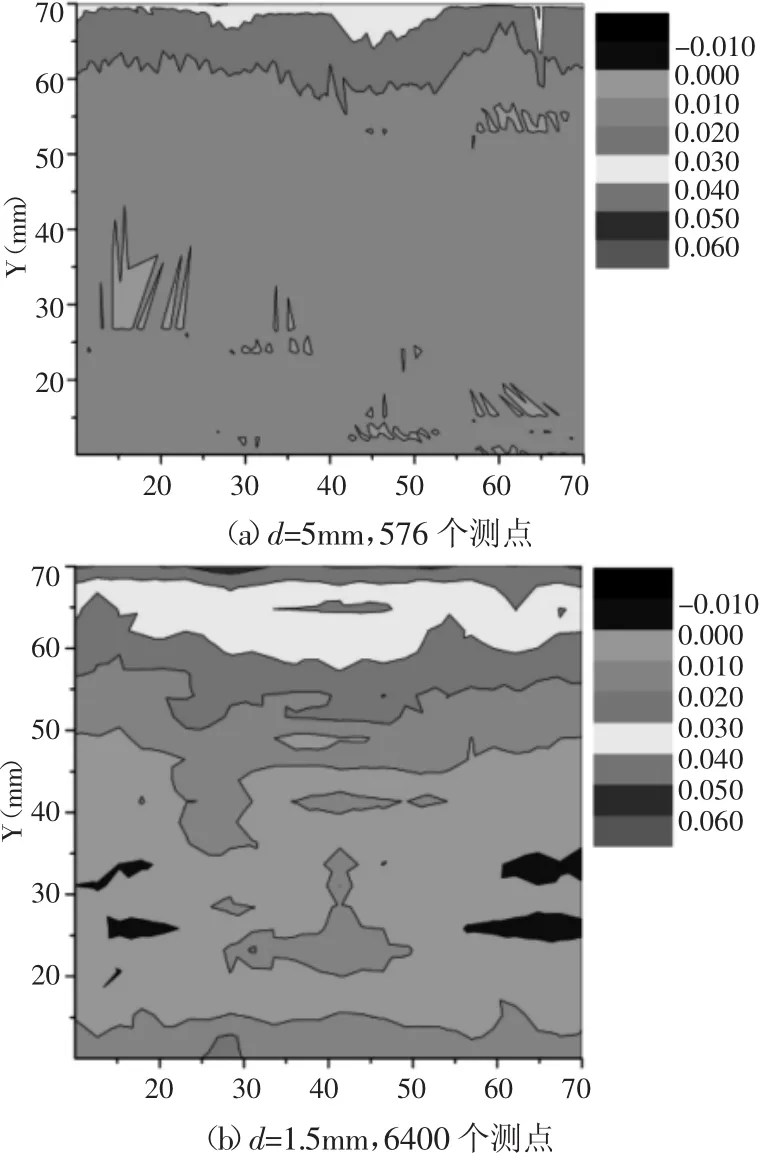
图7 法向偏差图Fig.7 Normal Devations

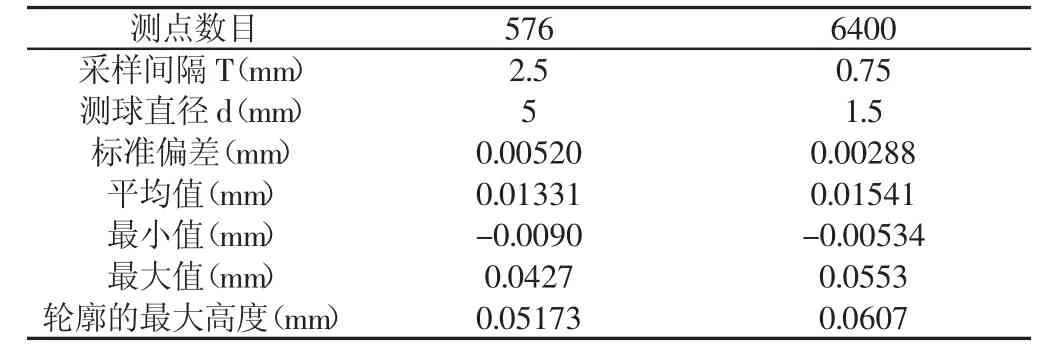
表3 曲面法向偏差Tab.3 Normal Devations of Surface

4 结论

针对复杂曲面，研究了不同的采样间隔和测球直径对曲面法向偏差的影响。研究了三种不同的采样间隔对曲面测量精度的影响，可以发现：在同一测球直径下，采样间隔越小，则测量得到的曲面坐标数据更能有效地反映曲面的实际轮廓，从而提高了复杂曲面测量精度，保证零件检测方法的合理性。此外，分析了不同测球直径对复杂曲面测量的影响，即：在相同采样间隔下，测球直径越小，更容易测量到复杂曲面轮廓的波谷，保证测量结果的准确性。最后，研究了在保持的采样参数比例下，改变和的值对测量效果的影响，得出当和同时取较小值时，曲面的测量精度更高。深入研究了不同因素对曲面法向偏差测量结果的影响，将对今后复杂曲面三坐标测量参数选取具有一定的指导意义。

［1］陈岳坪，靳龙，李书平.复杂曲面的形状误差评定方法研究［J］.机械设计与制造，2014（7）：215-7.（Chen Yue-ping，Jin Long，Li Shu-ping.Method of form error evaluation for complex surfaces［J］.Machinery Design&Manufacture，2014（7）：215-7.）［2］Adamczak，S.（2008）.Surface geometric measurements.Warsaw：WNT.（in Polish）

［3］卢耀晖，周继伟，张蔚.基于三坐标测量机的平面测量方法研究［J］.金属加工（冷加工），2012（1）：64-6.（Lu Yao-hui，Zhou Ji-wei，Zhang Wei.The method study based on plane measurements of coordinate measuring machines［J］.Metal Working（cold working），2012（1）：64-6.）

［4］Ainsworth I，Ristic M，Brujic D.CAD-Based Measurement Path Planning for Free-Form Shapes Using Contact Probes［J］.The International Journal of Advanced Manufacturing Technology，16（1）：23-31.

［5］Elkott DF，Elmaraghy HA，Elmaraghy WH.Automatic sampling for CMM inspection planning of free-form surfaces［J］.International Journal of Production Research，2002，40（11）：2653-76.

［6］Poon CY，Bhushan B.Comparison of surface roughness measurements by stylus profiler，AFM and non-contact optical profiler［J］.Wear.1995，190（1）：76-88.

［7］Bettge D，Starcevic J.Quantitative description of wear surfaces of disc brakes using interference microscopy［J］.Wear，2001，248（1-2）：121-7.

［8］曹旭，李明，韦庆玥.三坐标测量中测量点数对精度影响的研究［J］.机械制造，2013（4）：71-4.（Cao Xu，LI Ming，Wei Qing-yue.Research on the influence of measuring points on the accuracy in the CMM［J］.Machinery，2013（4）：71-4.）

［9］Poniatowska M.Deviation model based method of planning accuracy inspection of free-form surfaces using CMMs［J］.Measurement，2012，45（5）：927-37.

［10］Dong WP，Mainsah E，Stoutt KJ.Determination of appropriate sampling conditions for three-dimensional microtopography measurement［J］.International Journal of Machine Tools and Manufacture，1996，36（12）：1347-62.