基于AHP的供应链合作伙伴选择方法研究

余鹏飞，李 明，刘 湘，熊宗慧，巴智勇

（新疆大学 机械工程学院，乌鲁木齐 830047）

1 研究背景

随着信息化时代的到来，市场竞争加剧，企业所处的外部环境发生了巨大的变化，传统的企业运行方式已经无法应对信息化时代的挑战，如果还是固步自封、封闭式管理，最终只会被淘汰。面对激烈的市场竞争，企业必须联合上、下游企业，建立一条经济利益相连、业务相连紧密的供应链。供应链上的企业不再是单纯的业务往来，核心企业、供应商、分销商、客户之间是利益休戚与共的伙伴关系，共同分担市场竞争环境中的风险，达到“双赢”的效果。

供应链专家马丁·克里斯托弗说：“21世纪的市场是一个没有企业只有供应链的时代，供应链之间的竞争主导着市场的竞争。”所以选择合适的供应链合作伙伴成为企业当前的迫切需求。选择合作伙伴是供应链协作关系正常运行的基础，只有科学、正确地选择合作伙伴，才能真正实现供应链合作关系整体利益。建立供应链合作伙伴关系就意味着链上企业不再是一味地追求价格，而是更多地追求技术品质、质量攻关和整体的售后服务。供应链合作伙伴选择需要考虑方方面面的因素，同时合作伙伴之间必须有相同的战略目标，这就给合作伙伴选择增加了更大的难度。目前,供应链合作伙伴的选择方法主要有招标法、直观判断法、协商选择法、ABC成本法、AHP（层次分析法）、人工神经网络算法及模糊综合评价法等。本文主要采用AHP（层次分析法）对供应链合作伙伴选择进行研究。

2 供应链合作伙伴选择指标体系

企业在选择合作伙伴的时候，主观判断成分居多，存在根据企业印象和人际关系来确定合作伙伴的情况，选择过程掺杂太多的主观因素。企业选择合作伙伴所依据的标准体系不够健全，现存的选择标准主要是根据企业产品的质量、交货期和价格等方面，没有一个成型的供应链合作伙伴标准体系，这样很难对企业做出全面、客观、详实的评价。

企业选择供应链合作伙伴之前应先建立选择指标体系，指标体系建立需要遵循以下几个原则。①整体性。企业在选择合作伙伴时，应从整体上把企业的信誉、设备因素、质量成本、技术创新和交货期等各个方面的因素，全部纳入所要考虑的范畴。同时，企业要建立综合的评价指标体系，对企业做出全面、客观、详实的评价。②稳定性。评价指标体系应稳定运行，不受外界干扰，杜绝主观因素。③灵活性。评价指标体系应该灵活运行，不能生搬硬套，要根据企业的实际情况，灵活运用指标。同时，评价指标体系也要根据具体的情况进行不断丰富、扩展。④针对性。设置评价指标体系，企业应该对重要的合作伙伴和次要合作伙伴有所区分，尤其是对具有企业战略意义的合作伙伴，应该充分考虑各种定性和定量指标。企业在充分考虑合作伙伴的信誉、产品质量、成本、技术创新、交货期、售后服务等的基础上，坚持以上原则，并建立了一个供应链合作伙伴选择体系，如图1所示。

3 基于AHP方法的供应链合作伙伴选择

目前，AHP（层次分析法）方法已经被广泛认为是简单、有效的多目标决策方法。它综合考虑了客观因素和主观因素，将定性与定量结合起来，把一个复杂问题的相关组成因素按照内在联系分组，形成有序的递阶层次结构，通过两两因素之间的对比方式，确定各因素的相对重要性，同时合理有效地利用人的经验和判断力确定各因素的重要性排序，为供应链合作伙伴选择提供理性判断。AHP方法可以有效处理那些很难用简单的数学解析形式或者是难以完全定量解决的问题，由于它的这种广泛应用的特性，AHP方法为现实生活中的多目标、多规则决策问题提供了解决途径。AHP方法评价选择供应链合作伙伴的过程如图2所示。

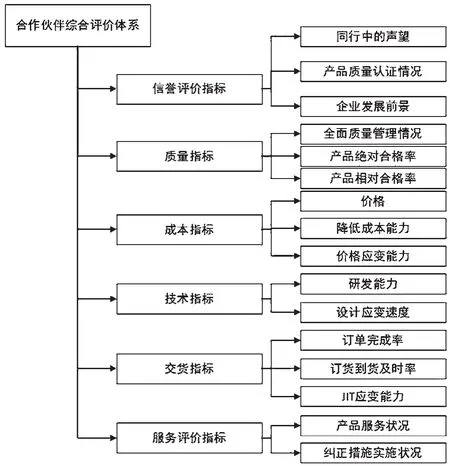
图1 供应链合作伙伴选择体系结构

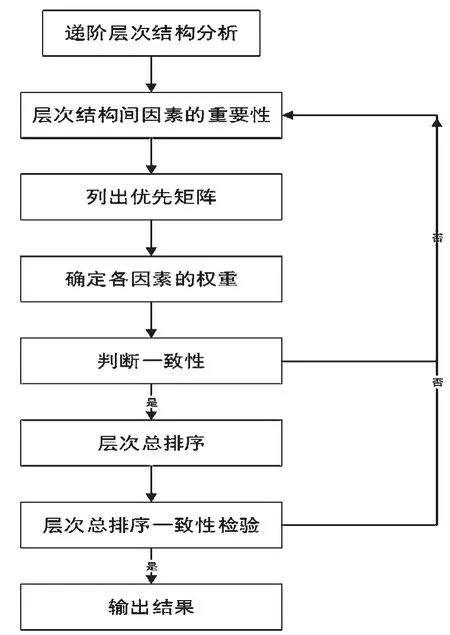
图2 AHP方法过程

3.1 建立递阶层次结构

首先明确问题所涉及的因素，并对其进行分类，同时建立一个各因素之间相互关联的递阶层次结构模型。其中顶层是目标层，一般只有一个因素，中间层为准则层，最底层为决策层。层次结构模型如图3所示。

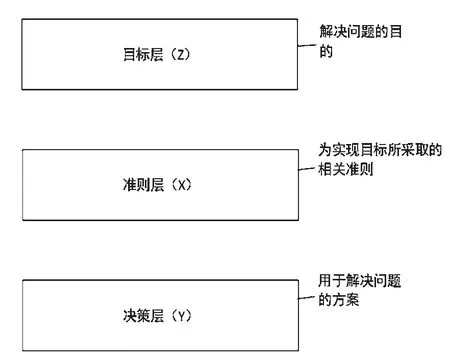
图3 AHP方法层次结构模型

3.2 构造判断矩阵

对于同一层次的元素，通过两两重要度比较，组成模糊比较矩阵。设模糊比较矩阵A=(Xij)n×n，同时满足Xij=1/Xji，Xii=1。在特定的情况下，模糊比较矩阵的元素具有传递性，且满足一致性要求。模糊判断矩阵的形式如下。

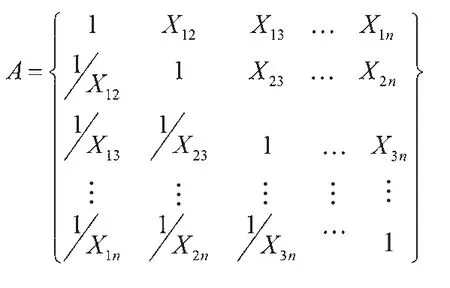
要比较同一层因素对上一层因素的影响，比较他们对于目标层Z的重要性。元素比较比例标度如表1所示。

表1 相对比较比例标度

3.3 数据量化处理

根据上面的判断矩阵，计算判断矩阵A的最大特征根βmax和经过归一化处理的特征向量集w=(w1,w2,…,wn)T。首先根据判断矩阵A，求得其最大特征根，再根据公式Aw=βmaxw，求得特征向量W并将所得结果归一化处理，将归一化处理所得出的特征向量w=(w1,w2,…,wn)T作为本层次元素X1，X2，…，Xn对目标层Z的排序权重。

3.4 判断矩阵的一致性检验

检验判断矩阵的一致性是要求矩阵中的元素满足Xij×Xjk=Xik，决策者根据各元素的相互重要性对评判矩阵各元素赋值，但是有时也会出现违背逻辑一致性的情况，比如“A比B重要，B比C重要，但是C比A重要”。为了防止判断矩阵一致性偏离太大，需要对判断矩阵的一致性指标CI进行检验。

正常情况下，低阶的判断矩阵（一阶或二阶）具有完全的一致性，但是对于高阶矩阵，它的一致性指标CI跟同阶的一般随机一致性指标RI之比，称之为判断矩阵的随机一致性比例，CR=CI/RI。当CR＜0.1时，判断矩阵A的一致性在允许范围内，当CR＞0.1时，判断矩阵A的一致性需要修正。平均随机一致性指标如表2所示。

表2 平均随机一致性指标RI

3.5 判断矩阵各层次元素权重计算排序

经过上述的计算可以得出其中一组元素对上层元素的权重向量，但是，最后需要得到所有元素对总目标的权重，尤其是最低层的元素对总目标的权重合成。合成权重的计算是自上而下的，将单一准则下的权重进行合成计算，并对其进行一致性检验。综合各层次元素相对于总目标的优先权重排序，得出各层次的总排序，决策者根据总排序做出选择。

4 结 语

供应链合作伙伴选择是企业发展的必经之路，当前我国企业已经认识到合作伙伴选择的重要性，但是选择合作伙伴的方法缺少系统研究，大多是根据自己的主观意愿去选择合作伙伴，从长远来看，这种选择方法会给企业带来很多损失。本文结合国内外对供应链合作伙伴选择方法的研究，提出用层次分析法来解决供应链合作伙伴的选择问题。同时，本文建立了一套供应链合作伙伴选择的指标，按照指标体系，并结合层次分析法对合作伙伴进行选择。但是，层次分析法也有一定的缺点，AHP方法最后只是给出了各合作伙伴的权重排序，最后选择哪一个作为合作伙伴，还需要决策者更多的信息评价。

［1］刘伯超.供应链合作伙伴选择研究［D］.长春：吉林大学,2007.

［2］柳青,黄道.基于AHP-BP算法的供应链合作伙伴选择建模及其应用［J］.华东理工大学学报：自然科学版,2007(1).

［3］苏仕宾,杨茂盛.基于可拓层次分析法的动态供应链合作伙伴选择［J］.物流技术,2005(11).

［4］陆锦洪,陈畴镛.基于AHP的供应链合作伙伴选择［J］.杭州电子工业学院学报,2001(3).

［5］马新安,张列平,冯芸.供应链合作伙伴关系与合作伙伴选择［J］.工业工程与管理,2000(4).