基于MapReduce离散萤火虫群优化算法的服务选择方法
,,,
(1.合肥工业大学 a.管理学院;b.过程优化与智能决策教育部重点实验,合肥 230009; 2.北京航空航天大学 自动化科学与电气工程学院,北京 100191)
0 概述
Web服务作为一种新型的分布式计算模型,已经成为面向服务架构(Service Oriented Architecture,SOA)和云计算软件即服务(Software as a Service,SaaS)的主要技术之一[1]。随着Web服务技术的日益成熟和服务的不断加入,出现了大量在网络上稳定易用且功能相对单一的Web服务,但是单个Web服务能够提供的功能有限,难以快速地满足用户复杂和多变的需求[2]。将现有的多个小粒度Web服务组合成一条增值的大粒度服务链来满足用户需求成为必然趋势[3]。因此,服务组合技术已成为云计算按需服务的关键技术和研究热点。
目前,基于服务质量(Quality of Service,QoS)的Web服务动态选择方法主要有两种,一种是基于QoS的局部优化原则,另一种是基于QoS的全局最优原则。基于QoS局部最优的Web服务选择是在每个服务类候选集中通过加权和排序选择局部最优的服务,但是不能保证组合服务整体最优[4];将基于QoS全局最优的服务动态选择问题转化为一个带QoS约束的多目标服务组合优化问题,目前有遗传算法、粒子群、整数规划[5-7]等方法求解全局最优组合问题,但是存在收敛速度慢、易陷入局部最优问题。而对于云环境下的大规模服务,搜索空间膨胀,造成组合效率低下的问题,云计算技术则提供了很好的支持,如云计算环境下的并行蚁群算法[8]、并行粒子群算法[9]等,将智能算法进行并行化,可高效、快速地解决海量数据的问题。
萤火虫群优化(Glowworm Swarm Optimization,GSO)算法是一种群智能优化算法[10]。该算法已应用于连续型和离散型论域优化,如多模态函数优化问题[11]、旅行商问题[12]、属性选择问题[13]、聚类[14]等多个领域。服务动态选择的实质是多条件多目标下的离散组合优化问题,但是在云计算环境下离散萤火虫群优化算法的研究甚少。本文研究在云计算环境下的离散萤火虫群优化算法的并行实现方法,提出基于MapReduce的并行离散萤火虫群优化算法(MRDGSO)。该算法融合分群分治思想,定义MRDGSO的Map过程和Reduce过程,加快收敛速度和避免陷入局部最优,并且针对Web服务选择问题,重新定义个体的编码、计算个体间的距离,改进位置更新、非可行解处理以及相关参数。
1 问题定义和描述
1.1 Web服务定义
对面向SaaS平台的大量功能相同而非功能属性不同的Web服务给出相关定义如下。
具体服务(Concrete Service,CS):由服务提供者在统一描述、发现和集成(Universal Description Discovery and Integration,UDDI)注册中心中注册的可执行的Web服务[15],记为:CS={D,F,Q}。其中,D表示服务的信息属性集合,F表示服务的功能属性集合,Q表示服务的质量属性集合。
抽象服务(Abstract Service,AS):仅描述服务的功能和接口信息,对应于某个服务候选集,是构成一条服务链的基本逻辑单元。一个AS包含多个CS,且这些CS由不同服务提供者提供,具有不同的QoS值,记为AS={CS1,CS2,…,CSh}。
服务组合(Service Composition,SC):为每个抽象服务AS从其包含的具体服务中根据QoS选定出具体服务,所形成的可执行具体服务链,记为SC={AS1,AS2,…,ASm},表示每一个服务组合SC由m个AS组成,而每一个AS由k个功能相同的候选CS组成,每一个CS有nq个QoS属性{QoSn1,QoSn2,…,QoSnq}。
服务质量(QoS):是Web服务的一组非功能特性,包括响应时间、吞吐量、可靠性、可用性、安全性、真实度等。本文主要考虑Web服务的5种QoS属性,分别为执行时间T、执行费用C、信誉度Rep、可靠性Rel和可用性Ava。这也是目前较常用和具有代表性的QoS属性。
1.2 基于QoS服务选择问题描述
QoS全局最优Web服务选择就是在Web服务组合中,对各个抽象服务相对应的候选服务集中分别选择出一个具体服务,形成一条可执行的服务链,使得服务链满足QoS约束的前提下,整体的QoS达到最优[16]。将服务组合中基于QoS的服务选择问题定义如下模型,如图1所示。
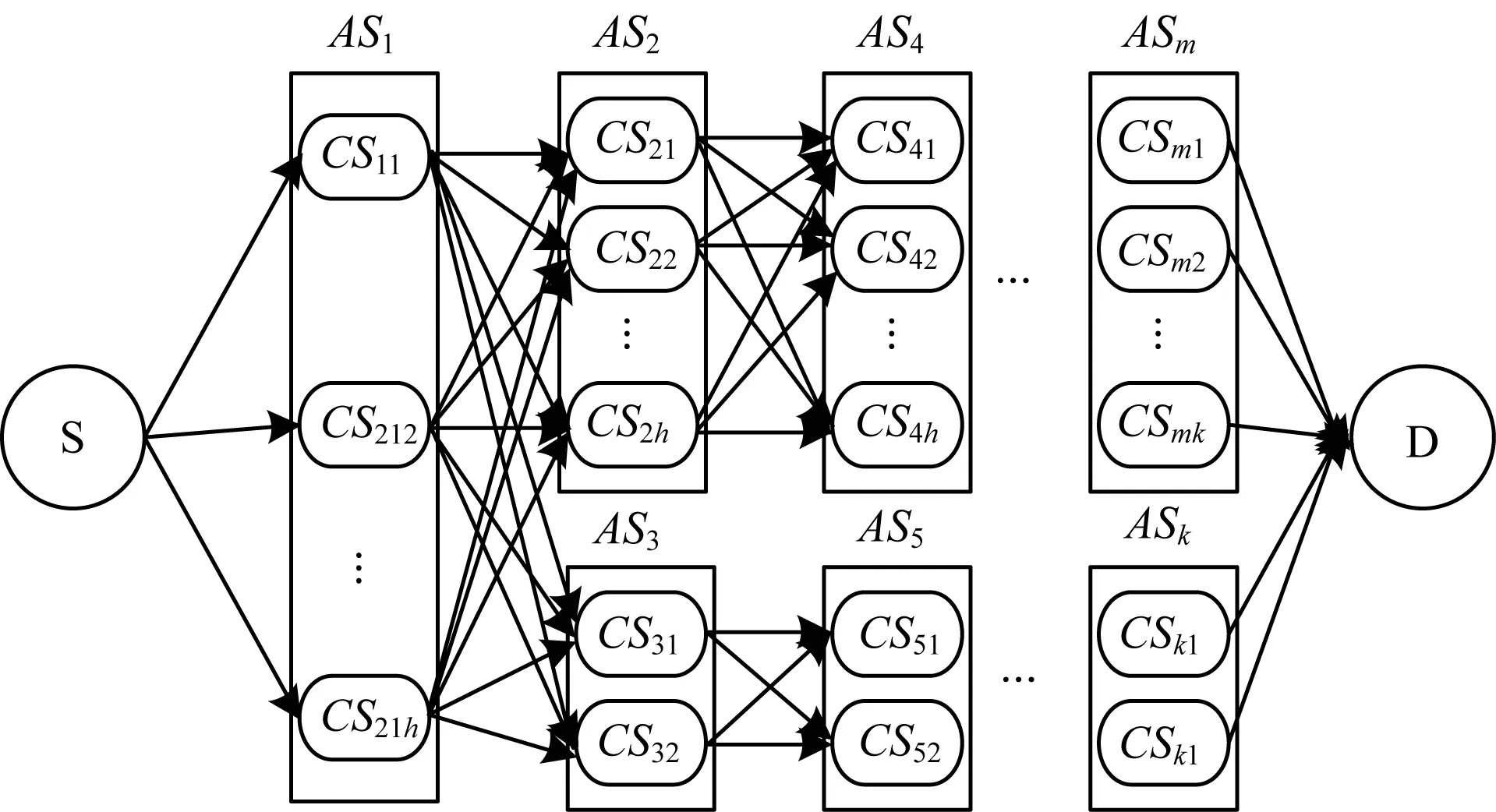
图1 服务组合
服务组合(SC)由AS1,AS2,…,ASm,m个抽象服务组成,而每个AS由h个候选功能相同而非功能属性不同的CS组成,表示为ASm={CSm1,CSm2,…,CSmh},每一个CS有nq个服务质量属性QoSn1,QoSn2,…,QoSnq,那么SC={CS1j,CS2j,…,CSmj}(j=1,2,…,h)表示满足用户需求的其中一个服务组合。服务组合就是在每一个抽象服务中选出一个具体服务,并且满足整体QoS属性达到最优。对应于上述服务组合图,QoS全局最优Web服务选择问题可转化为一个求从S到D的带QoS约束条件下的多目标最优路径问题,则一个带QoS约束的多目标服务组合优化模型形式化描述可表示如下:
(1)
其中,T(sc)为服务组合执行花费的总时间,C(sc)为服务组合执行花费的总成本,T(sc)和C(sc)作为2个性能评价准则,Rep(sc)表示为服务组合执行的信誉度,Rel(sc)表示为服务组合执行的可靠性,Ava(sc)表示为服务组合执行的可用性,Rep(sc)、Rel(sc)和Ava(sc)作为3个约束条件。
2 基本的萤火虫群优化算法
GSO通过模拟自然界萤火虫求偶或觅食行为,聚集在一个或多个点,该点即为最优解。GSO算法主要包含4个阶段,即萤火虫初始化、萤光素更新、位置更新和决策半径更新[17]。算法流程如下:
步骤1初始化。在可行域中随机生成n个萤火虫,初始化每个萤火虫的萤光素l0、动态决策域r0、感知域rs、移动步长S、邻域阈值nt、萤光素消失率ρ、萤光素更新率γ、动态决策域更新率β、最大迭代次数Tmax。
步骤2萤光素更新。对于极小值问题按式(2)进行更新:
li(t)=(1-ρ)li(t-1)+γ1/f(xi(t))
(2)
其中,f(xi(t))表示萤火虫i在t时刻所在位置的目标函数值,li(t)表示萤火虫i在t时刻的萤光素值。
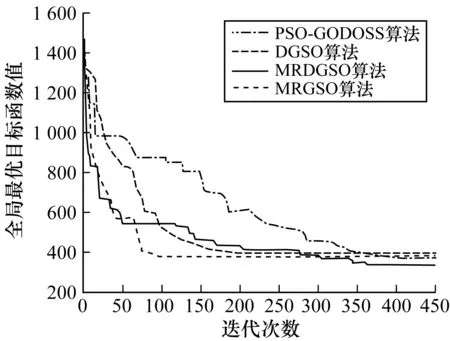
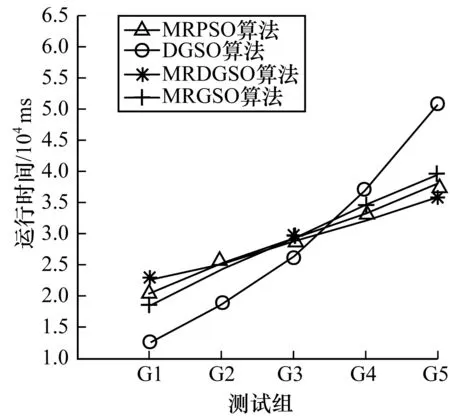
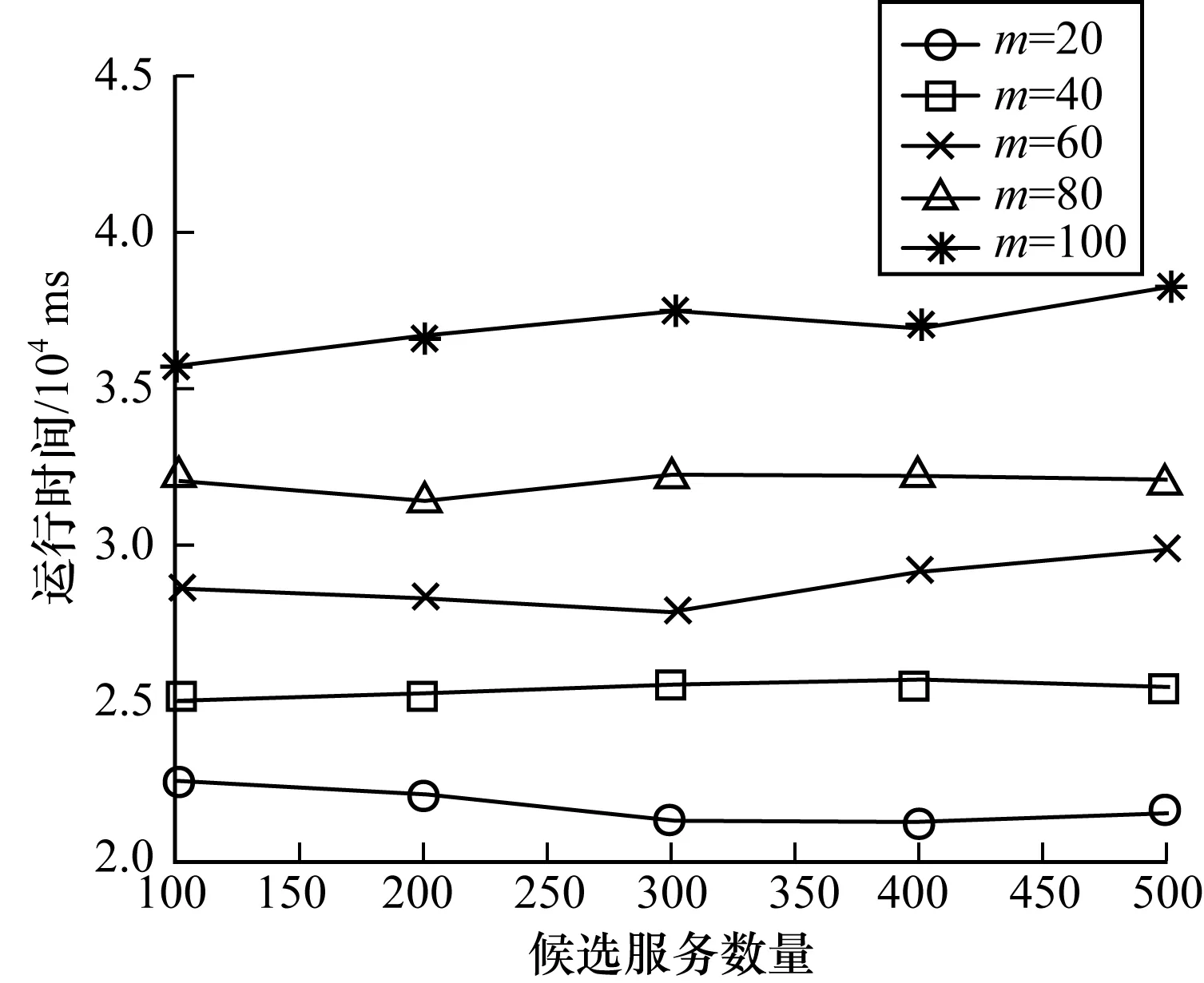
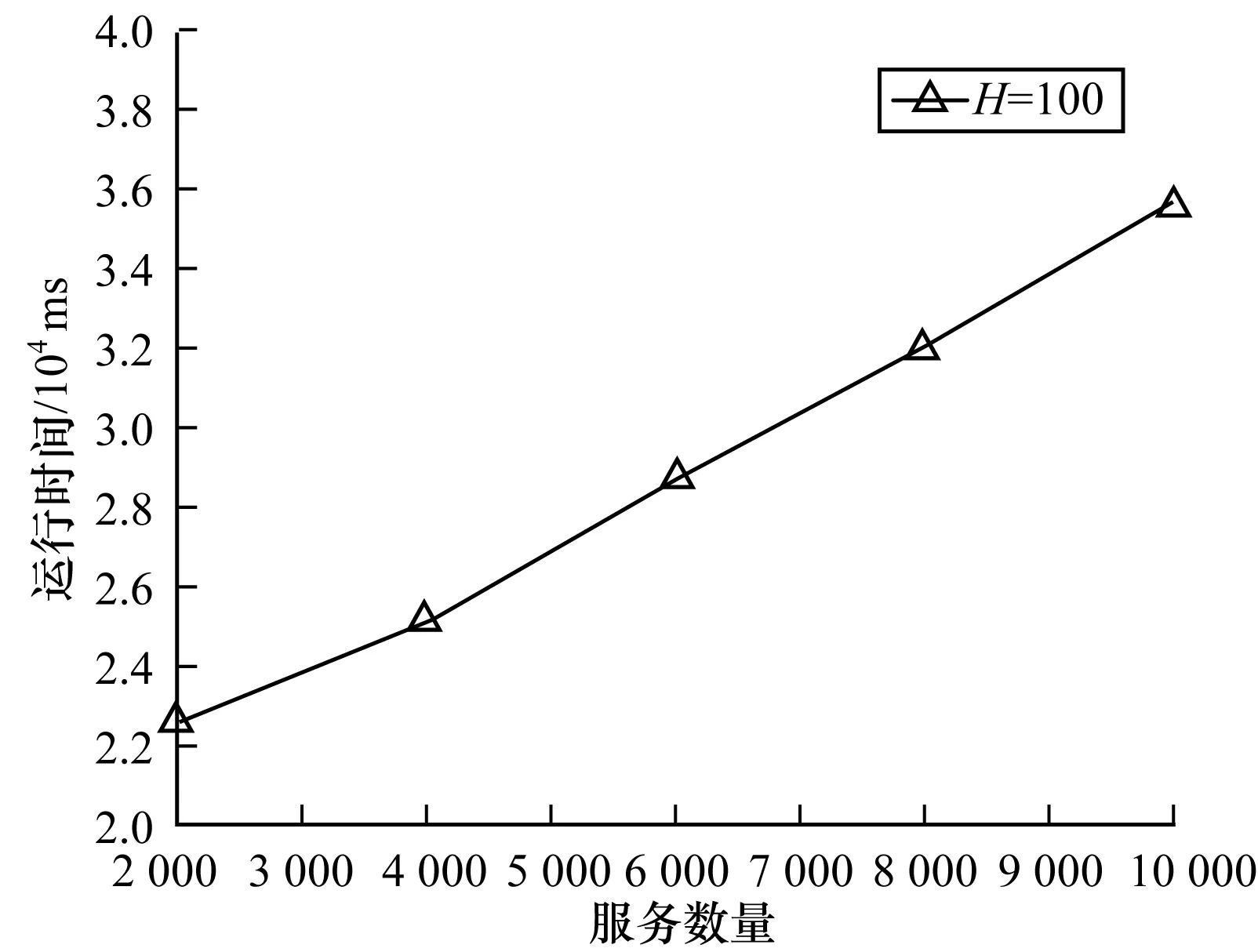
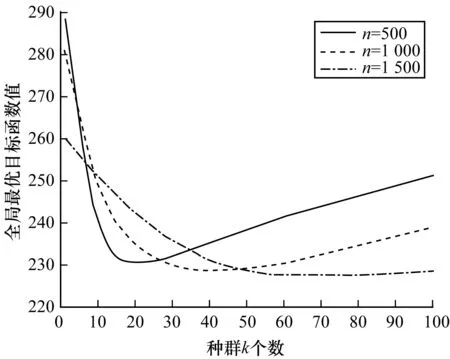
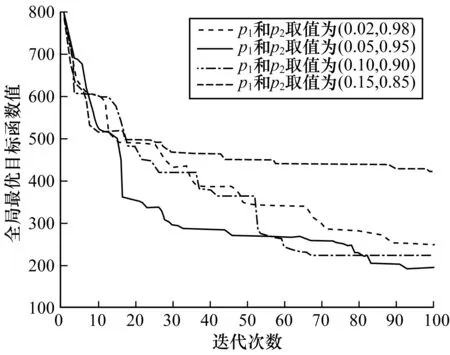
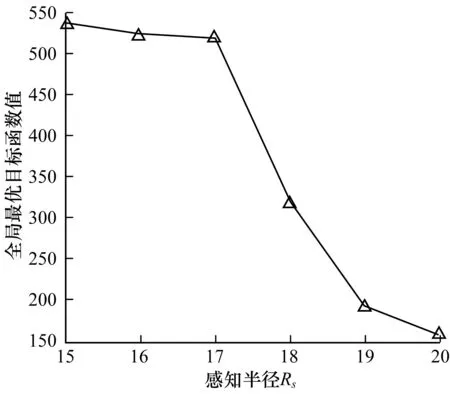
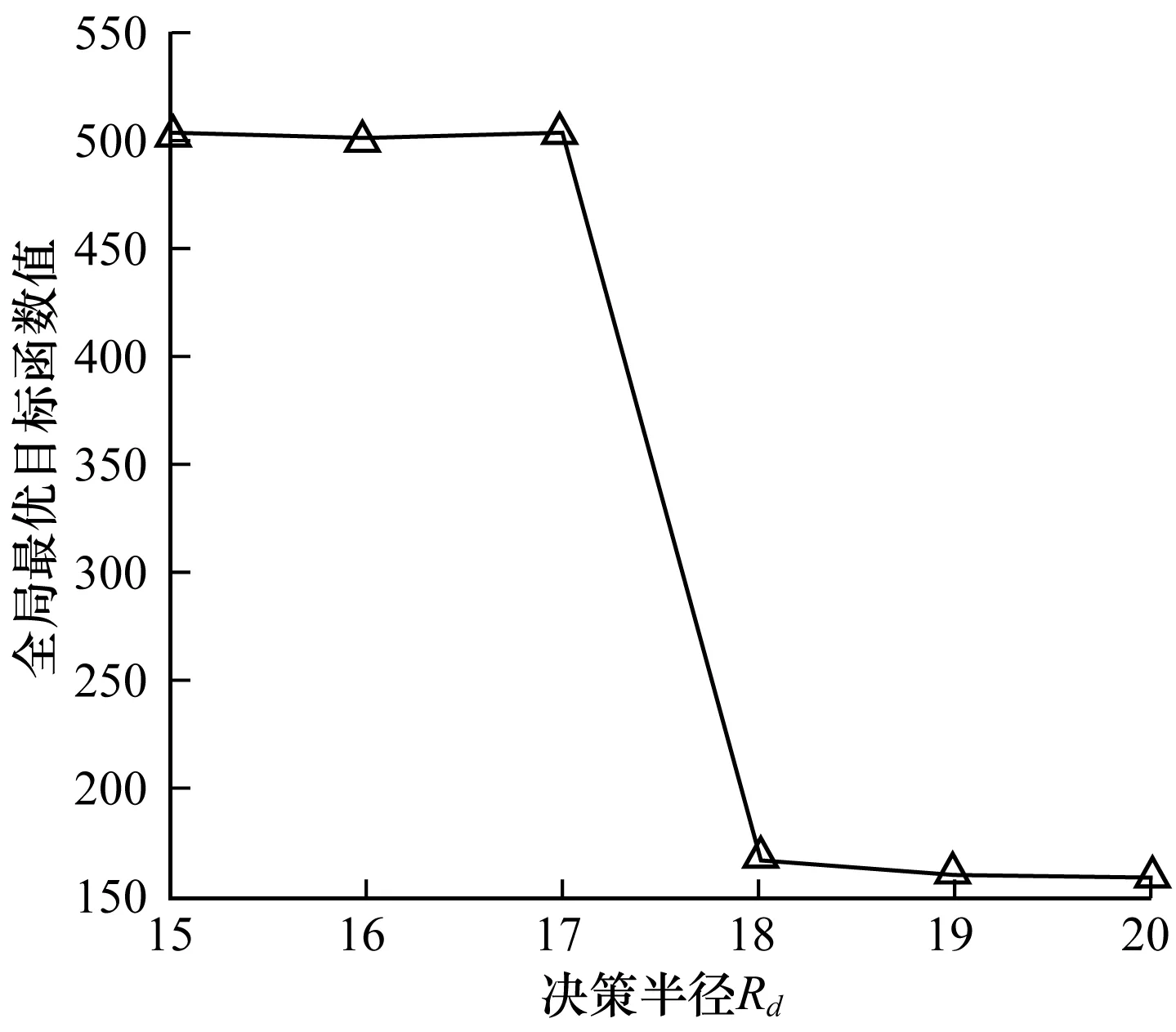
Ni(t)={j:‖xj(t)-xi(t)‖ (3) (4) (5) 步骤4按式(6)更新决策半径: β(nt-|Ni(t)|))) (6) 其中,|Ni(t)|为邻域集内的萤火虫数量。 MRDGSO运用云计算的MapReduce编程模式[18]将离散萤火虫群优化算法并行化,设计出离散萤火虫群优化算法、Map函数和Reduce函数,并针对服务组合优化问题,重新定义了个体的编码、距离计算、目标函数、改进位置移动方式。借鉴分群分治的思想,融入到MRDGSO算法中,实现云环境下小规模多种群[19]并行计算,改善算法搜索速度慢和易于陷入局部最优的缺点,提高求解效率和对海量数据的处理能力。MRDGSO融合分群分治思想的执行过程如图2所示。 图2 MRDGSO执行过程 文献[20]针对多模态函数提出了基于MapReduce的萤火虫群优化算法,改善了搜索计算耗时和大规模问题求解效率低的缺点。本文进一步优化,将分群分治思想融入到改进的DGSO算法中,具有快速和高效地求解高维海量数据的能力。 MRDGSO主要分为4个阶段,即初始化阶段、分群搜索阶段、优良解保留阶段和合并搜索阶段。 步骤1在初始化阶段创建一个初始的萤火虫群,在给定的搜索空间内采用空间分割法[21]随机生成m维的初始位置Xi,并对目标函数J、萤光素L0和决策半径Rd0进行初始化,最后将所有萤火虫平均分配在不同的种群中,以萤火虫位置信息、目标函数信息、萤光素信息、决策半径信息和种群信息组成的萤火虫结构体形式进行存储,萤火虫结构体形式如图3所示。其中,K表示萤火虫群的种群编号,i表示萤火虫编号。最后在给定的Web服务集合中计算出理想点T*、C*。 图3萤火虫结构体 步骤2在分群搜索阶段应用Map函数分别对不同的种群用DGSO算法独立搜索,并行萤火虫算法中最耗时的部分——萤火虫之间的距离计算和邻域搜索,应用Reduce函数来更新萤火虫的萤光素、目标函数,并保存种群内的最优解,最后将更新后的萤火虫以结构体形式作为输出结果,作为下一代Map函数的输入,反复循环迭代,直至所有种群收敛或满足阈值。 步骤3在优良解保留阶段保留K个种群的优良解。在合并整个可行域的解时,通过控制算法的感知域Rs来控制萤火虫的飞行范围,从而实现在不同种群之间的信息共享。 步骤4在合并搜索阶段将保留下来的优良解作为新的萤火虫群初始位置,应用MapReduce计算模型搜索全局最优解,直至种群收敛或满足阈值。 文献[12]中的离散萤火虫群优化算法在求解离散组合优化问题时,简单、易实现而且鲁棒性强。应用DGSO解决服务组合问题的关键是解向量构造和初始化、萤火虫个体间距离计算、目标函数构造、萤火虫个体位置更新和非可行解处理。 1)解向量构造和初始化。本文基于符号的编码,将每只萤火虫的序列编码看作一个组合服务,序列编码中的每个元素对应于服务候选集中的一个具体服务编号,其解向量编码表示为:Xi=(Xi1,Xi2,…,Xik),Xik∈[1,Hk]。其中,Xi表示第i只萤火虫,不同的萤火虫表示不同的服务组合,Xik表示第i只萤火虫在第k个服务类下的具体服务编号,取值为区间[1,Hk]上的整数。在MapReduce模式下的萤火虫结构体为:Gi=(Xi,J(Xi),Li,Rdi,Ki),其信息包含基本的萤火虫位置Xi、目标函数J(Xi)、萤光素Li、决策半径Rdi和种群编号Ki。初始解采用文献[21]中的区间分割法生成,在解空间上均匀分布,保证随机产生的各个解向量具有差别性并且满足QoS多约束条件,以避免陷入局部最优,增强了全局搜索的能力。 2)个体间距离计算公式。萤火虫个体间的距离由维度间距离和维度内距离两部分组成,由维度间距离引导维度内距离,使得相同的维度数量越多,距离越小,其次在相同的维度数量情况下,维度内距离越小,则距离越小。设个体i、j在第t次迭代的位置编码分别为序列xi(t)=(xi1,xi2,…,xik)和xj(t)=(xj1,xj2,…,xjk),则个体i、j在第t次迭代的距离计算公式定义为: (7) (8) (9) 其中,dij(t,k)表示xj(t,k)-xi(t,k),1/m是维度引导系数,Hk是第k维度上的取值上限,也指在服务组合上第k个抽象服务的候选服务数量,C为常数,表示距离系数。由式(9)可知dij(t)∈[0,C],个体i、j之间的距离满足对称性,即dij=dji。参数C取值太大或者太小都不利于邻域集更新。 3)目标函数构造。本文将多目标问题转化为单目标优化问题来求解全局QoS最优,求得的最优解作为多目标的最优解,采用TOPSIS法构造目标函数。 (10) 其中,f+(k)表示为第k个抽象服务的QoS理想解。 对于约束条件下的单目标求最小化问题则表示为: f+=min{f(m)|R(m)≥R0,k∈[1,m]} 对于约束条件下的单目标求最大化问题则表示为: f+=max{f(m)|R(m)≥R0,k∈[1,m]} 4)萤火虫个体位置更新。对于求解离散组合优化问题,DGSO算法是在各维上相同位置则保持不变,不同位置则以一定的概率选择更新公式进行更新,从而实现整个位置的更新。具体更新公式如下: xik(t+1) (11) 5)非可行解处理。在每次迭代过程中,某些解向量有可能不满足于约束条件或者偏离可行解域,成为非可行解。在进入下一次迭代之前,丢弃本次迭代中所有非可行解,采用上述区间分割法随机产生可行解替换非可行解,并且重新初始化其决策半径,从而提高搜索效率和保持种群多样性。 Map函数的任务是分别对k个种群内的个体萤火虫i在其各自的种群内独自搜索,将萤火虫最耗时的邻域搜索和位置更新并行化,得到新位置的个体萤火虫i,同时更新移动后的决策半径。Map函数输出的 函数1MRDGSO的Map函数 Function Map(Key,value) 1.Ki←key,Ni←Ø 2.Xi,J(Xi),Li,Rdi,Ki←getInfo(value) 3.Temp←getTempSwarm(distributedCache) //HDFS Distributed Cache 4.for each j∈Temp do 5.Xj,J(Xj),Lj,Rdj,Kj←getInfo(Temp) 6.dij←getDistance(Xi, Xj)// using Equation (9) 7. if (dij< Rdiand Li< Ljand Ki= Kj) then Ni←Ni∪j // using Equation (3) 8.end for 9.if (|Ni|>0) then 10. for each j∈Nido 11. Pij←getProbability(Li,Lj) 12. end for 13.end if 14.Xi←getBestNeighbor(Pij) 15.Xnew←getNewX(Xi,Xj)//using Equation (11) 16.Rdnew←getNewRd(Rdi,| Ni|) // using Equation (6) 17.Glowwormnew←setInfo(Xnew, J(Xi), Li, Rdnew) 18.Emit(Ki, Glowwormnew) End Reduce函数的任务是对Map产生的新位置的萤火虫i更新萤光素,并根据QoS属性值利用理想点法更新萤火虫的目标函数值,选出当前种群内最优的服务组合,保存当前种群内萤火虫的最优解。Reduce函数输出的 函数2MRDGSO的Reduce函数 Function Reduce(key,valueList) 1.K←key;Glowwormbest←Ø ; 2.for each j∈valueList 3. Xj,J(Xj),Lj,Rdj,Kj←getInfo(valueList) 4. Jnew(Xj)←getNewJ(Xj)//using Equation (10) 5. Lnew←getNewL(Lj, Jnew(Xj)) //using Equation (2) 6. Glowwormnew←setInfo(Xj, Jnew(Xj), Lnew, Rdj) 7. Emit(K, Glowwormnew) 8.end for End 设萤火虫总数目为n,种群数为k,有效迭代次数为Titer,Web服务总规模为N,抽象服务的属性个数为m。则算法时间复杂度分析如下: 1)第1阶段初始化解的过程时间复杂度为O(n+N)。 2)一次迭代中,第2阶段Map函数的总时间复杂度为O(mn2/k)。 3)一次迭代中,第2阶段Reduce函数的总时间复杂度为O(n)。 4)第3阶段保留种群优良解过程的总时间复杂度为O(n2/k)。 5)一次迭代中,第4阶段Map函数的总时间复杂度为O(mk2)。 6)一次迭代中,第4阶段Reduce函数的总时间复杂度为O(k)。 故迭代Titer次的算法时间复杂度为: 本文实验硬件环境:Inter Core i5处理器;内存为4 GB;64位Linux操作系统;3台VMware。实验所需的软件包括Centos 6.5、Hadoop-0.20.0、JDK1.7.0、Eclipse4.5。将其中1台主机节点作为master,其他2台主机节点作为slave,搭建hadoop集群。根据文献[12]中建议的参数,并结合本文多次实验,将MRDGSO参数设置选定如表1所示。 表1 DGSO参数设置 此外,式(8)、式(10)分别取值为C=20,p1=0.05,p2=0.95。 本文的实验测试数据参照文献[8]中随机方式生成各具体服务CS的QoS值,QoS的取值范围为:0 表2 各组不同规模的测试数据 4.2.1 可行性和有效性分析 为了验证本文算法的可行性和有效性,引入了文献[2]中的基于粒子群进化的服务选择算法(PSO-GODSS)、文献[20]中的MRGSO算法和传统的DGSO进行比较。图4给出了PSO-GODSS、MRGSO、DGSO、MRDGSO在基于上文所述的QoS评价指标上的实验结果,并且采用G1组规模下对算法性能进行测试,发现在该G1组规模下迭代第30次之前,MRDGSO、MRGSO和DGSO算法前期收敛速度略快于PSO-GODSS,而迭代第45次时DGSO算法陷入局部最优,迭代第84次时MRGSO算法陷入局部最优,迭代第100次时PSO-GODSS算法陷入局部最优,MRDGSO算法在第315次达到全局最优解,其全局搜索能力略优于其他算法。图5给出了上述算法在G2组规模下对算法性能的测试结果,发现在较大规模服务下MRDGSO算法的收敛速度和全局搜索能力明显优于DGSO和PSO-GODSS算法,而在全局搜索能力上优于MRGSO算法。 图4 在G1组下的全局最优收敛过程 图5 在G2组下全局最优收敛过程 表3给出了MRPSO、DGSO、MRDGSO、MRGSO算法分别在不同规模下求得的全局最优解及其所消耗的时间结果,其中MRPSO是上述PSO-GODSS在MapReduce框架下实现的并行化,可以看出MRDGSO的全局搜索能力表现优秀,始终优于DGSO和MPRPSO。而在G1、G2和G3数据,并行化的MRDGSO、MRGSO和MRPSO运行时间比非并行的DGSO慢,而在大规模服务G4和G5下并行算法明显比非并行的快。图6展示了4种算法在不同服务规模下的运行时间走势情况,从而体现了MRDGSO并行算法求解大规模问题的优势,也进一步从执行效率上证明了MRDGSO算法的可行性和有效性。 表3 4种算法在不同服务规模下的全局最优解及其计算代价 图6 3种算法在不同服务规模下的运行时间 综合上述实验表明,本文提出的MRDGSO算法在求解服务选择问题上具有可行性和有效性,且其求解全局QoS最优在解的质量上和算法性能上均比PSO-GODSS、MRPSO、DGSO算法有显著提升。 4.2.2 MRDGSO的扩展性及性能分析 图7给出了抽象服务AS数量m分别为20、40、60、80、100,候选服务数H从100增加到500,并以100为步长,统计出MRDGSO算法进行服务选择执行20次的平均计算时间开销。实验结果表明,候选服务数量的变化对算法时间没有明显的影响,而抽象服务规模越大,算法运行时间越长。图8给出了候选服务数H固定为100,服务数量N从2 000增加到10 000,即抽象服务AS数量以步长20从20增加到100,统计出MRDGSO算法进行服务选择执行20次的平均计算时间开销。实验结果表明,服务数量的增加或者抽象服务AS数量的增加,算法运行时间呈现增长的趋势。说明该算法有良好的扩展性,而且能够应对大规模服务集合的组合问题。 图7 候选服务数量对本文算法性能的影响 图8 服务数量对本文算法性能的影响 在云计算平台Hadoop下,MRDGSO实现并行化的实际时间开销除了平台自身消耗以外,还跟所选取的mapper数量有关。设定每个节点最多可运行10个mapper,那么整个map的容量是10×3(节点)=30个。图9给出了在给定10 000个变量的总规模下,随着mapper数量的增加所消耗的时间逐渐减小,而超过30个mapper时,由于资源缺乏而无法容纳更多的mapper,每次迭代所耗费的时间会增加。 图9 在恒定规模问题下本文算法的可扩展性 图10给出了在每个mapper设置为150个变量下,开始随着mapper数量的增加逐渐上升,然后随着mapper数量的增加不会改变迭代时间。在mapper数量达到30个后,map的容量饱和导致迭代时间略有增加。 图10 在恒定负载下本文算法的可扩展性 综合上述实验,表明本文提出的MRDGSO并行化算法有良好的可扩展性,克服了离散萤火虫群优化算法解决服务选择问题计算效率低的困难,而且能够处理大规模问题。但也存在以下不足:1)用Map函数并行计算萤火虫邻域集在计算耗时问题上可进一步优化;2)Reduce函数并不适应计算所有问题的评价函数;3)由于MapReduce模型的一些限制,并未表现出其线性扩展性。 4.2.3 参数分析 图11给出了参数n和k对MRDGSO算法的影响结果,展示了在G1组规模和萤火虫总数n分别为500、1 000和1 500的种群规模下,MRDGSO分成种群k与n之间的关系。从图中可以看出,在一定的萤火虫群体规模下,随着分成种群k数量的不断增加,全局最优搜索能力先是逐渐增强,当k达到一定值后又逐渐降低;当n=500时,k在[15,30]范围内全局搜索能力最强,当n=1 000时,k在[35,50]范围内全局搜索能力最强,当n=1 500时,k在[60,80]范围内全局搜索能力最强;满足n/k∈[15,30]时,即每个种群的萤火虫数量控制在[15,30]范围内,全局搜索能力最强。 图11 n和k对本文算法性能的影响 MRDGSO算法在求解服务选择离散组合问题的关键在于p1和p2参数的取值,直接影响算法的收敛速度和全局搜索能力。图12给出了参数p1和p2对MRDGSO算法的影响结果,展示了在G1服务规模下,不同的p1和p2取值对算法性能的影响。从图中可以说明不同的参数p1和p2取值影响算法的收敛速度和全局搜索能力。当p1和p2取值为(0.05,0.95)时,MRDGSO收敛速度最快,全局搜索能力最强;当p1和p2取值为(0.15,0.85)时,MRDGSO收敛速度最慢,全局搜索能力最差;当p1和p2取值为(0.02,0.98)和(0.10,0.90)时,MRDGSO收敛速度较慢,全局搜索能力还未达到最强。 图12 参数p1和p2对本文算法性能的影响 由式(9)中可知,2个萤火虫个体之间的距离dij(t)∈[0,C],引入距离系数C,且设置为20,使得所有的萤火虫个体之间的距离在[0,20]范围内,而其感知半径和决策半径的大小直接引导着萤火虫的搜索方向和最优解的质量。图13给出了在G1服务规模下参数Rs对本文算法的影响。从图中可以看出,感知半径Rs=20时,全局搜索能力最强。图14给出了在G1服务规模下,且Rs固定为20,参数Rd对本文算法的影响。从图中可以看出,决策半径Rd在[18,20]范围内,求得的全局最优解质量较高,且当Rd=20时,全局搜索能力最强。综合上述实验,对参数感知半径和初始决策半径设置为Rs=Rd=20,p1和p2设置为p1=0.05,p2=0.95,n和k的设置为n/k∈[15,30]。 图13 感知半径对本文算法性能的影响 图14 决策半径对本文算法性能的影响 针对云计算下大规模服务组合中的QoS全局最优Web服务选择问题,本文在云计算平台下利用MapReduce计算模型实现了离散萤火虫群优化算法并行化,提出了求解该问题的基于MapReduce的并行离散萤火虫群优化算法。对传统的DGSO算法进行了改进,设计了离散萤火虫群优化算法、Map函数和Reduce函数,并将分群分治思想融入到算法中,避免算法过早陷入局部最优,加快算法收敛速度和提高算法的全局搜索能力。实验结果表明,MRDGSO算法在服务选择问题上得到了成功的应用,具有对高维和大规模问题的求解能力,表现出良好的扩展性。今后将针对MRDGSO算法存在的问题作进一步改进,使之应用到其他领域上,扩展算法的实际应用价值。 [1] 刘 旋,廖明潮.基于人工鱼群算法的QoS全局最优Web服务选择的研究[J].计算机应用与软件,2013,30(8):87-90. [2] 康国胜,刘建勋,唐明董,等.QoS全局最优动态Web服务选择算法[J].小型微型计算机系统,2013,34(1):73-76. [3] 倪志伟,吴 昊,尹道明,等.云和声搜索算法及其在知识服务组合中的应用[J].计算机应用究,2013,30(3):806-809. [4] 刘书雷,刘云翔,张 帆,等.一种服务聚合中QoS全局最优服务动态选择算法[J].软件学报,2007,18(3):646-656. [5] 张成文.基于遗传算法的具有全局QoS限制的Web服务选择[D].北京:北京邮电大学,2007. [6] 范小芹,蒋昌俊,方贤文,等.基于离散微粒群算法的动态Web服务选择[J].计算机研究与发展,2010,47(1):147-156. [7] ZENG Liangzhao,BENATALLAH B,DUMAS M,et al.Web Engineering:Quality Driven Web Service Composition[C]//Proceedings of World Wide Web Conference.New York,USA:ACM Press,2003:411-421. [8] 王会颍,倪志伟,伍章俊.基于MapReduce和多目标蚁群算法的多租户服务定制算法[J].模式识别与人工智能,2014,27(12):1105-1116. [9] MCNABB A W,MONSON C K,SEPPI K D.Paralled PSO Using MapReduce[C]//Proceedings of the Congress on Evolutionary Computation.Singapore:[s.n.],2007:7-14. [10] KRISHNANAND K N,GHOSE D.Glowworm Swarm Based Optimization Algorithm for Multimodal Functions with Collective Robotics Applications[J].Multiagent & Grid Systems,2006,2(3):209-222. [11] KRISHNANAND K N,GHOSE D.Glowworm Swarm Optimization for Simultaneous Capture of Multiple Local Optima of Multimodal Functions[J].Swarm Intelligence,2009,3(2):87-124. [12] 周永权,黄正新,刘洪霞.求解TSP问题的离散型萤火虫群优化算法[J].电子学报,2012,40(6):1164-1170. [13] 倪志伟,肖宏旺,伍章俊,等.基于改进离散型萤火虫群优化算法和分形维数的属性选择方法[J].模式识别与人工智能,2013,26(12):1169-1178. [14] ALJARAH I,LUDWIG S A.A New Clustering Approach Based on Glowworm Swarm Optimization[C]//Proceedings of IEEE Congress on Evolutionary Computation.Washington D.C.,USA:IEEE Press,2013:2642-2649. [15] 龚小勇,朱庆生.支持QoS的Web服务选择模型的研究与实现[J].计算机工程,2008,34(24):55-57. [16] 康国胜,刘建勋,唐明董,等.基于差异演化算法的QoS全局最优动态Web服务选择[J].电信科学,2011,27(12):67-71. [17] 祝华正.萤火虫群算法的改进及其应用[D].南宁:广西民族大学,2011. [18] JIN C,VECCHIOLA C,BUYYA R.An Extension of MapReduce for Parallelizing Genetic Algorithms[C]//Proceedings of the 4th International Conference on Escience.Washington D.C.,USA:IEEE Press,2008:214-221. [19] 祝华正,何登旭.一种小规模多种群萤火虫群优化算法[J].计算机工程与应用,2011,47(23):48-50. [20] ALJARAH I,LUDWIG S A.A MapReduce Based Glowworm Swarm Optimization Approach for Multimodal Functions[J].Swarm Intelligence,2013,8237:22-31. [21] ZHANG Kangli,CHEN Shouyuan,SHAO Zengzhen.The Improvement of Harmony Search Algorithm[J].Artificial Intelligence and Robotics Research,2015,4(4):32-39.3 求解服务选择问题的MRDGSO算法
3.1 MRDGSO并行化设计
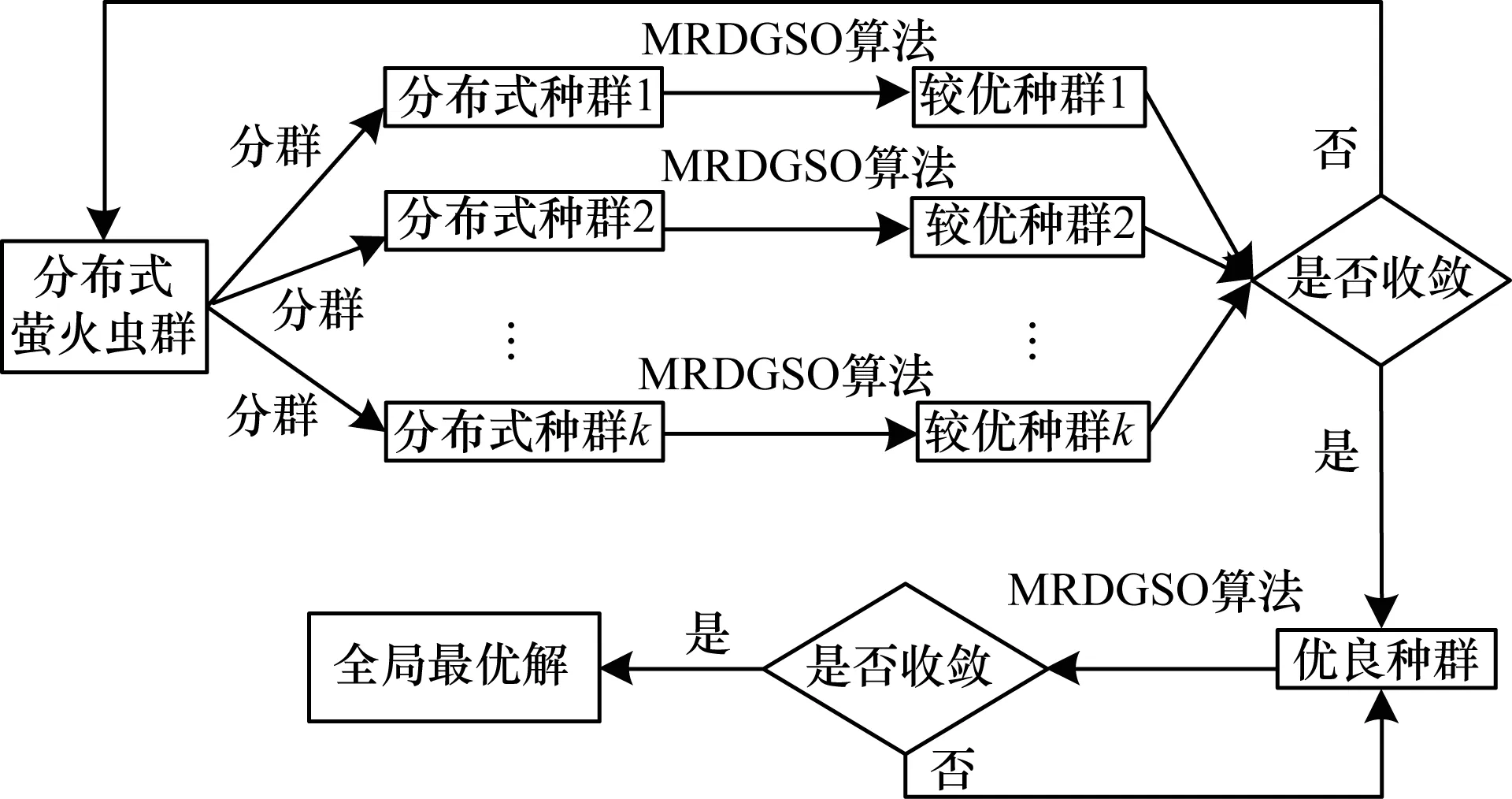

3.2 离散萤火虫群优化求解方法
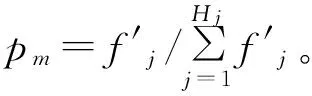
3.3 Map函数设计
3.4 Reduce函数设计
3.5 时间复杂度分析
4 实验及结果分析
4.1 实验设置

4.2 结果分析




5 结束语

