公路规则梁桥地震易损性模型及简化计算方法

陈力波， 黄才贵， 黄勇冰， 栗怀广

(1.福州大学土木工程学院，福建福州350108;2.西南交通大学土木工程学院，四川成都610031)

桥梁结构作为交通运输工程生命线的重要组成，在地震发生时往往遭受较大程度的损坏，也因此造成巨大的经济损失.作为公路交通系统地震风险评价的重要环节，桥梁地震易损性分析对震后应急决策提出和桥梁抗震评估与加固等都具有相当重要的指导意义.桥梁地震易损性通常采用易损性函数进行刻画，即为不同地震动水平作用下桥梁结构达到特定损伤状态的概率.20世纪90年代以来，在遭受了如1995年阪神地震、1999年集集地震、2008年汶川地震所造成的惨痛损失后，国内外学者对桥梁地震易损性展开了较为广泛的研究.文献［1］基于阪神地震资料和桥梁损伤数据结合最大似然估计法，对桥梁的地震易损性进行分析，评估桥梁的破坏类型和损伤状态;文献［2］统计了美国洛杉矶Northridge地震震后的桥梁破坏数据，并根据桥梁结构进行分类，按对数正态分布假定回归得到了各类桥梁的地震易损性曲线和参数;文献［3-4］基于桥梁的震害调查数据，采用数理统计建立了经验型地震易损性模型的方法.另一方面针对这些地区典型桥型，采用不同分析手段和方法建立了分析型地震易损性模型.文献［5］通过人工合成的地震动记录，对位于New Madrid地震带的连续梁桥进行地震易损性分析并得到其易损性曲线;文献［6］采用一阶可靠度理论对美国的一座典型公路桥梁展开地震易损性分析;文献［7］考虑了外部环境对桥梁结构的侵蚀作用，对多跨连续梁桥进行时变易损性分析;文献［8］考虑墩高、配箍率和支座类型的差异性，对新规范设计下的双柱式连续规则梁桥这一特定类型的桥梁进行地震易损性研究.

目前，美国、日本和台湾地区已将桥梁地震易损性模型纳入桥梁抗震评估及加固的相关手册或报告中，为区域范围内的桥梁抗震加固优先级决策提供依据［9-11］.鉴于我国现有公路桥梁现状与美、日、台等地区存在巨大差异，上述3个国家和地区的研究只能作为参考.我国在桥梁易损性应用领域的研究尚有欠缺，多数学者仅针对某特定桥例或某一类特定桥型开展地震易损性模型研究，少有学者考虑桥梁结构参数的变异性对桥梁系统地震易损性的影响，尚未形成典型公路桥梁的分类地震易损性模型.此外既往研究中，数值分析所需耗费的计算量较大，对我国数量庞大且迅速增长的桥梁而言，不利于易损性模型的进一步推广及应用.

本文以我国公路规则梁桥作为研究对象，根据不同上部结构支承形式、墩柱形式和设计规范细化桥型，建立分析型地震易损性模型，并展开模型参数化研究.得到桥梁地震易损性中位值的简化计算公式，同时给出了对数标准差的建议值，为后续桥梁抗震评估及加固决策提供参考和依据.

1 桥梁样本建构与非线性有限元分析

1.1 桥梁分类

本文主要研究对象为公路规则梁桥，其常见的上部结构支承形式包含简支梁和连续梁，常见的墩柱形式有单柱式和双柱式，同时考虑到在2008年《公路桥梁抗震设计细则》(JTG/T B02-01—2008)［12］颁布之后(以下简称《08 抗震细则》)，桥梁抗震设计标准更加严格，桥梁相应的抗震性能也得到提高.新旧规范的差异性主要体现在桥墩的配筋率与配箍率取值的不同要求.

基于上述考虑，在确定桥梁样本参数之前，本文依据上部结构支承形式、墩柱形式和设计规范年限对公路规则梁桥进行了分类.表1给出了公路规则梁桥的分类及其代号，其中，旧规范指按《公路工程抗震设计规范》(JTJ 004—1989)［13］所设计的桥梁样本(以下简称《89抗震规范》)，新规范指按《08抗震细则》所设计的桥梁样本.

1.1.1 上部结构参数

我国公路规则梁桥常用的上部结构主要有空心板、T梁和箱梁3种形式.对于公路规则梁桥，它包含着不同的上部结构截面形式、不同的跨径、不同的桥面宽度等参数信息.查阅公路桥梁上部结构通用图，可以得到这3种形式上部结构的基本参数分布情况.本文综合考虑了各种截面形式参数的分布情况，对每一类桥型分别设计出10种不同的上部结构样本，包括2种空心板梁、4种箱梁和4种T梁.

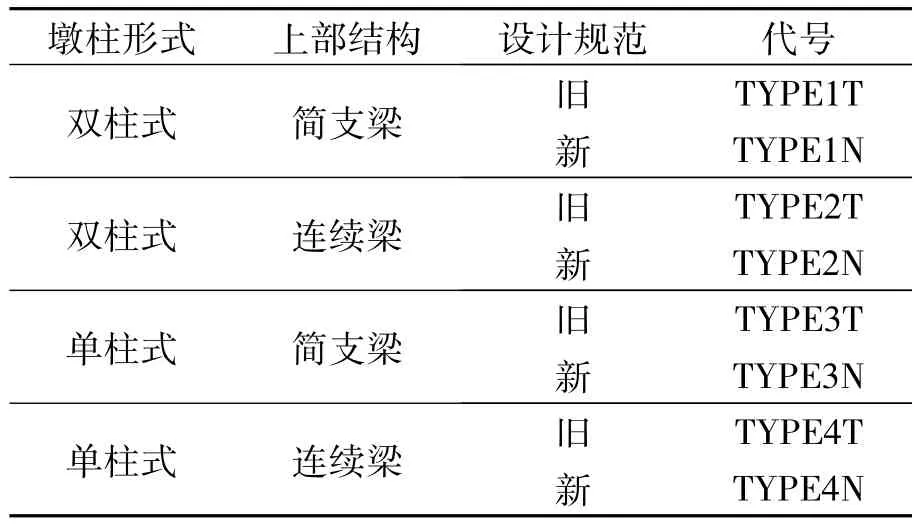
表1 公路规则梁桥桥型分类Tab.1 Category of regular highway girder bridges

1.1.2 墩柱参数

实际工程中墩柱参数受地形和地基的影响，形式是多种多样的，没有通用的标准图提供选择.本文确定桥梁墩柱样本是在考虑墩柱本身参数的不确定性和符合规范关于规则梁桥界定标准的基础上，采用随机抽样的方法生成桥梁墩柱样本.选择圆形截面作为桥梁墩柱截面，以下对相关因素进行逐项分析.

(1)墩柱截面直径

基于实际桥梁工程的统计并结合现有的一些调查数据，对于公路规则梁桥而言墩柱截面尺寸与桥梁跨径之间存在一定的关系，伴随上部结构跨径增大及上部结构总质量增大，墩柱作为承受上部质量的构件，其截面也会随之增大.针对不同的墩柱形式采用10种墩径，整体范围为1～2 m，间隔为0.1 m.基于前述提出的每种上部结构，采用3种墩柱直径与其相配，并随机分布在8个样本中.

(2)墩柱高度

公路规则梁桥的墩高变化范围也较广，根据《08抗震细则》中的定义，本文选择规则梁桥的墩高范围不大于 30 m，且桥墩长细比为 2.5～10.0.由于墩柱截面直径已经确定，在同时满足以上两项规定的前提下，对每一类上部结构形式的桥梁采用4种墩高，随着跨径和墩柱截面直径变化而不同，整体分布在4～18 m，间隔2、3 m或4 m，同样先是采用随机分布与已有墩柱截面和上部结构组合成样本，若不满足上述规则梁桥要求，则再对样本进行个别调整.

(3)配筋率、配箍率

从现有的调查统计资料看，配筋率、配箍率是分布最广的参数.新旧规范也对墩柱配筋率、配箍率进行了部分限定，具体如表2所示.

表2 新旧规范对墩柱配筋率、配箍率的规定Tab.2 Provisionsfor reinforcement ratio and stirrupratio by old＆newly specification %

新规范对桥梁的配筋要求更高，按照新规范设计的桥梁配筋率、配箍率相对更大，因此本文采用不同的配筋率、配箍率来区别新旧规范设计桥梁的类别.根据调查统计资料结合工程实际经验，分析确定了双柱式和单柱式的配筋率、配箍率范围.假定其符合均匀分布并随机抽样选出具体数值进行配筋.

(4)材料参数

墩柱的材料包含混凝土和钢筋，为了使每类桥梁的情况更符合实际公路桥梁，对墩柱的材料进行了设计.由统计资料可知，墩柱的混凝土等级主要为 C30、C35，钢筋主要为 HRB335，也有部分为HRB400.对每类桥梁的墩柱样本材料设计为:混凝土等级 C30、C35各 40个;钢筋等级 HRB335、HRB400分别为60、20个.同样采用随机抽样，随机分布在各个样本中.

1.1.3 其他构件参数

盖梁采用正方形截面，边长假定为墩柱直径，盖梁的钢筋等级与混凝土等级与墩柱相同，配筋率、配箍率在墩柱的基础上有所提升，保证其有一定的承载能力.由上部结构的参数计算获知每个支座的支反力，依此查阅《公路桥梁板式橡胶支座规格系列》(JTT663—2006)［14］确定出具体支座规格，进而计算得到支座的水平刚度和竖向刚度.简支梁和连续梁有不同的支座布置形式和不同的传力方式，所得到的支座规格会有不同.本文为简支桥梁设计了4种规格支座，连续桥梁设计了5种规格支座.

综上分析，以新规范双柱式简支梁桥为例，建立基准桥梁流程图，如图1所示.

根据每类桥型的墩柱形式，在考虑跨径、截面宽度和截面形式等因素基础上，提出10种简支梁桥上部结构样本.参考双柱式桥墩对应的墩柱直径，墩高依据1.1.2节取值，同时随机抽取每个桥墩的配筋率和配箍率，在满足规范长细比规定基础上，生成112个桥墩样本.进一步考虑墩柱直径与上部结构跨径的对应关系，挑选得到80个合理的桥墩样本.将10种上部结构样本、4种支座类型随机匹配80个桥墩样本，得到新规范双柱式简支梁桥的80个桥梁样本.最后根据表1的桥梁分类，按照类似流程本文建构8种桥梁类型共计640个基准桥梁样本.

图1 设计流程Fig.1 Designing diagram

1.2 桥梁非线性动力有限元分析

本文选用Opensees(open system for earthquake engineering simulation)进行桥梁非线性动力有限元分析［15］.从既往震害分析可知，大多数梁桥其上部结构在地震中基本保持线弹性状态，因此采用三维弹性梁单元模拟主梁，依据前文计算得到主梁截面特性，将其赋予主梁单元.板式橡胶支座是我国公路规则桥梁较为常用的一种支座类型，在动力作用下的滞回曲线为狭长形，故采用零长度单元(zerolength element)来实现线弹性弹簧单元的模拟，依据规范计算支座单元的水平和竖向刚度将其赋予零长度单元.在地震作用下，桥墩和盖梁结构较易发生损伤，因此采用基于柔度法的非线性梁柱单元进行模拟［16］.单元截面采用纤维截面进行精细化模拟，通过纤维材料的本构关系可以确定截面恢复力与变形的关系，精确模拟截面的实际受力情况.选取修正后的Kent-Scott-Park本构模型即OpenSees材料库中的Concrete02 Material来模拟约束和无约束混凝土材料;选用Giuffre-Menegotto-Pinto本构模型，即OpenSees材料库中的Steel02 Material定义钢筋材料.综合计算成本，桥台部分采用简化方法进行模拟，将其作为支座处理;基础部分本文未考虑桩土效应对桥梁地震响应的影响，墩底采用固结处理.

地震动通常可以按来源分为实际测量的天然波以及合成的人工波.根据剪切波速的不同，对所选地震记录依照我国现行《公路桥梁抗震细则》的相应规定按场地类型进行了划分.从美国太平洋地震研究中心数据库和中国国家地震动台中心强震观测数据库中分别挑取Ⅰ类、Ⅱ类、Ⅲ类场地各80条地震波，合计240条地震记录，并按能量法［17］进行截断处理，以震级为标准来区分大小地震，以震中距来定义近远场地震.为了确保数值模拟更加真实地反映桥梁在实际遭受地震作用下的响应，采用三向地震波输入方式.由于本文研究需要对地震波进行多次调幅，并含有大量非线性动力计算分析，在综合考虑时间成本、计算代价及计算结果精确度后，选择地表峰值加速度PGA作为地震动强度指标.

采用前述建构的640个桥梁样本，针对不同的场地类别，随机选取地震波分别与640条地震动记录进行随机匹配，进一步完成增量动力分析［18-19］，通过回归计算得到桥梁构件及系统的地震易损性参数.有限元分析计算量较为庞大，包含8种桥型，每种桥型80个样本，分3类场地，每条地震波调幅10 次(0.1g～1.0g)，共计包含有19 200 次的非线性时程分析.

2 公路规则梁桥地震易损性分析

2.1 损伤指标及极限状态定义

在强地震动作用下，结构部分构件进入非线性状态，同时出现不同程度的损坏，如何准确描述构件的破坏程度并给出一个可靠的评估方法，一直是地震工程理论中的一个重要研究课题.既往研究者对破坏准则进行大量研究，提出了各种损伤等级［20］.对比各国的研究报告并结合考虑桥梁在震后的功能和修复要求，本文采用五级性能水准划分来细化公路规则梁桥的破坏程度，分为完好无损、轻微破坏、中等破坏、严重破坏、完全破坏.对于常见的公路规则梁桥而言，结构主要易损构件是墩柱和支座.

选取位移延性比作为墩柱抗震性能损伤指标，结合 Hwang等［21］和美国的 FEMA 协会［9］的研究对墩柱的极限状态进行定义.支座的抗震性能设计参数为剪切应变，结合日本规范［10］和文献［23］的研究确定极限状态.公路规则梁桥支座和桥墩5个性能水准的极限状态如表3所示.

表3 公路规则梁桥墩柱和支座极限状态Tab.3 Limit states of pier and bearing for regular highway girder bridges

2.2 桥梁构件及系统损伤概率分析

2.2.1 构件损伤概率分析

基于上述结果进一步计算桥梁构件地震易损性，由地震易损性定义可知，易损性为在给定地震动强度IM下，构件的地震需求DEDP大于其抗震能力CEDP的概率，如式(1)所示.

为了对此概率进行估计，式(1)可改写为

式中:N为地震动记录的样本数;Fi为构件的极限状态函数，其意义为地震动强度IM下第i组地震动记录，计算得到的构件抗震需求DEDP，i大于等于其抗震能力 CEDP，i时取值为 1，反之为 0，即

基于前述增量动力分析，可以计算得到不同地震动强度 IM，j(j=1，2，3，…，n)下构件发生损伤状态概率Pcomp的离散数据点.假设构件的易损性函数为对数正态分布函数，即

式中:mcomp、βcomp分别为构件易损性函数的中位值和对数标准差.

对式(4)进行最小二乘法回归，即可估计得到mcomp和 βcomp.

2.2.2 桥梁系统损伤概率分析

常规系统一般可以分为串联系统、并联系统和混合系统.考虑到桥梁构件极限状态反应了其在桥梁系统中的功能丧失程度，因此将桥梁结构系统界定为串联系统，即认为每个构件的破坏都会造成整个系统相同程度的破坏，构件的最大损伤等级就是系统的损伤等级，即

式中:DS，system为系统的损伤状态;DS，pier为桥墩的损伤状态;DS，Bearing为支座的损伤状态.

通过式(5)，统计出桥梁系统在每个PGA下发生某损伤等级的频数，将其除于样本数(式(2))，即可得到桥梁系统的损伤概率psys.假定桥梁系统地震易损性函数服从对数正态分布，则

式中:msys、βsys分别为系统易损性函数的参数中位值和对数标准差.

通过最小二乘法回归得到msys和βsys.

2.3 桥梁系统地震易损性模型

考虑不同的墩柱型式、上部结构类型和规范要求，从3类场地中分别挑取不同的地震波进行非线性动力时程分析，回归出易损性函数中的统计参数，包括中位值和对数标准差.分类桥梁在各类场地下的地震易损性参数如表4所示，同时给出了场地汇总(即忽略场地影响，只考虑桥梁类型的差异性)和桥梁汇总(即忽略桥梁类型的影响，只考虑场地的差异性)的中位值和对数标准差.

对上述计算结果进行分析讨论，具体如下:

(1)对比不同墩柱形式得到的地震易损性函数中位值，可以看出:墩柱形式对易损性函数中位值的结果影响较大，经计算两者结果的差值百分比全都大于17%，在组成规则梁桥的3个因素中，墩柱形式对易损性函数中位值起着较为重要的影响作用;任一类场地的中位值对比结果发现双柱式数值都比相应的单柱式数值要大，因此对于不同的墩柱形式，单柱式相对于双柱式更加易损.对比不同墩柱形式得到的地震易损性函数对数标准差存在一定的差异:墩柱形式对上部简支旧规范这类桥梁影响最小，对上部连续旧规范这类桥梁影响最大;上部连续旧规范、上部连续新规范这两类桥梁墩柱形式为双柱式时的对数标准差小于单柱式;上部简支旧规范和上部简支新规范两者对数标准差没有确定大小关系.

(2)对比新旧设计规范得到的桥梁系统地震易损性函数中位值可以看出:设计规范对易损性函数中位值的影响相比墩柱形式要小，两者结果的差值百分比大都介于7%～25%.任一类场地的中位值对比结果发现旧规范数值都比新规范数值要小.因此对于不同的设计规范，旧规范设计的桥梁相对于新规范设计的桥梁较易损，这与预期相符.对比不同设计规范得到的桥梁系统地震易损性函数对数标准差，可以看出:不同设计规范对双柱式梁桥影响较小，其差值百分比大都小于18%;对于双柱式简支这类桥梁，旧规范的对数标准差小于新规范;对于单柱式连续这类桥梁，旧规范的对数标准差大于新规范;双柱式连续和单柱式简支这两类桥梁，对数标准差没有确定的大小关系.

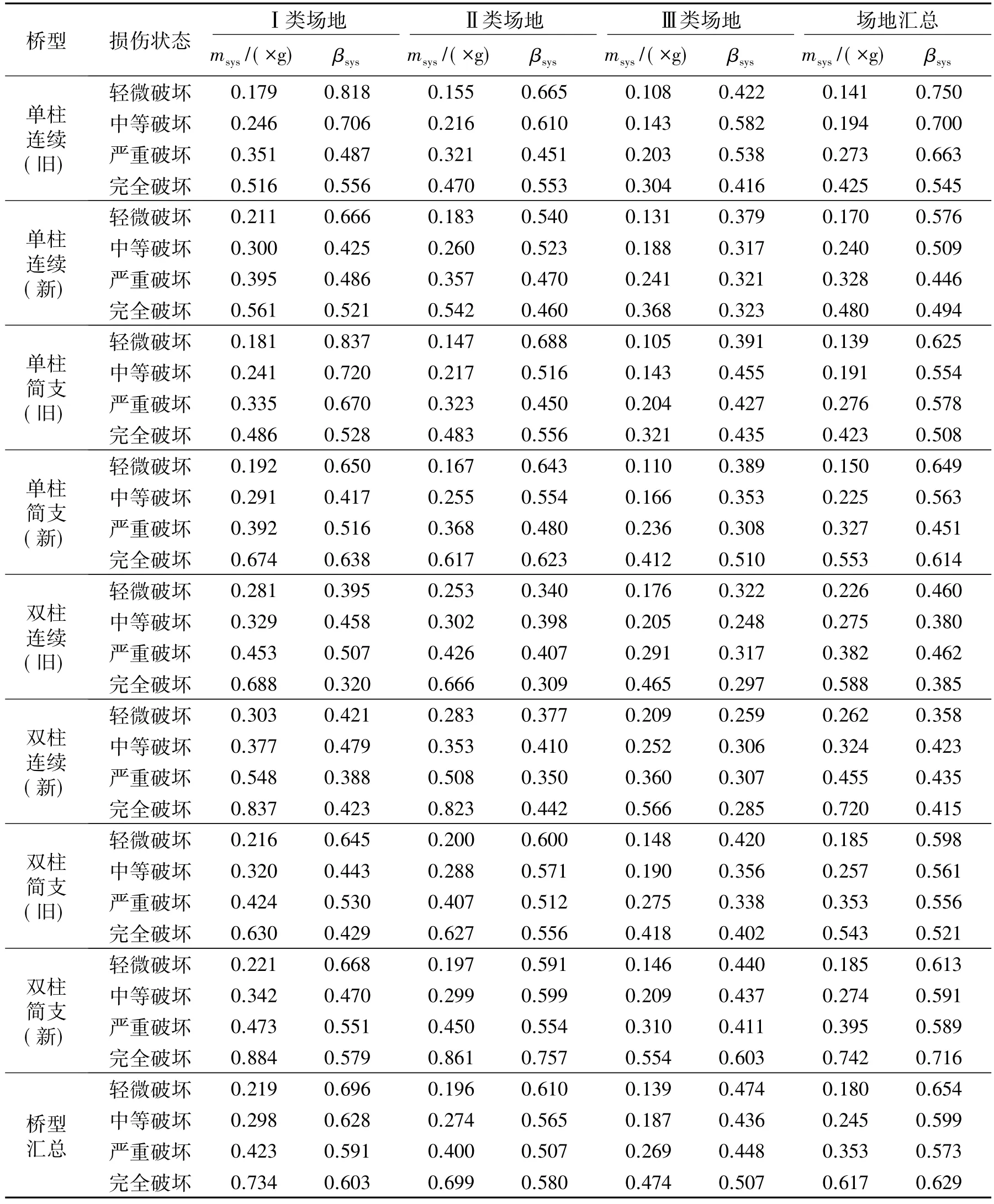
表4 公路规则梁桥各类场地下的地震易损性参数Tab.4 Seismic vulnerability parameters of regular highway girder bridges under the various fields

(3)对比不同上部结构支承形式得到的地震易损性函数中位值可以看出:上部结构形式对易损性函数中位值的结果影响较小，两者结果的差值百分比大都小于15%，特别是对单柱式旧规范这类桥梁的影响最小，4种损伤状态下两者的结果差值百分比都小于8%;对比任一类场地的中位值结果发现简支梁数值都比相应的连续梁数值要小.因此对于不同的上部结构支承形式，简支梁相对于连续梁较易损.对比不同上部结构支承形式得到的地震易损性函数对数标准差，结果存在一定规律:不同的上部结构支承形式对单柱式新规范这类桥型影响较小，对双柱式新规范这类桥影响最大;对于双柱式旧规范、双柱式新规范、单柱式新规范这三类桥梁，上部结构支承形式为简支时的对数标准差大于连续;对于单柱式旧规范这类桥梁，上部结构支承形式为简支梁时的对数标准差小于连续.

3 桥梁地震易损性简化计算方法

3.1 震易损性函数简化计算流程

综合考虑桥梁类别和场地类型的变异性对桥梁系统地震易损性的影响，建立典型公路桥梁的分类地震易损性模型.进一步针对典型公路桥梁地震易损性模型计算结果展开参数化研究，进而提出适用于我国公路规则梁桥的地震易损性简化计算方法.

先是采用统计回归方法，建立桥梁各分类汇总下的易损性中位值与各分类之间的线性关系，例如，已知桥墩汇总下的中位值，通过回归获得修正系数k，即可基于线性方程y=kx预测得到单柱和双柱的易损性中位值，结果表明误差均可控制在可接受的范围.因此参考台湾地区规范［11］，在已知各分类汇总中位值线性方程的前提下，通过系数的连乘方式，计算得到不同桥梁分类及不同场地类型的易损性函数中位值.然而计算结果显示简单的连乘导致结果与实际值误差较大，无法满足精度的要求.因此，本文将桥梁分类和场地类型归为定性变量，并假定各分类的水平数，采用哑变量－1、1代替桥梁分类，各类桥梁的哑变量取值如表5所示，用－1、0、1 分别代替Ⅰ类、Ⅱ类、Ⅲ类场地［23］，采用多元非线性回归方法建立易损性函数中位值与各分类之间关系，结果发现回归得到的公式过于复杂，未取得简化计算的目的.

综合上述两种计算思路，采用哑变量－1、1代替桥梁分类，通过多元线性回归方法计算出场地汇总下的易损性中位值，再通过线性回归的方式得到3类场地的易损性函数中位值.对于对数标准差，由于其描述桥梁发生损伤概率数据的离散程度没有实际的工程意义，所以均值化处理，详细简化计算流程如图2所示.

3.2 地震易损性函数中位值的简化

地震易损性函数中位值反应了桥梁达到某种损伤状态的概率为50%时所对应的地震峰值加速度值.本文综合考虑了公式的复杂程度与计算偏差之后，提出适合于我国公路规则梁桥的中位值简化计算公式.为了检验简化公式的拟合效果，采用均方误差EAvg、最大绝对误差Emax和均方根误差ERms来检验函数预测的效果［23］，分别如式(7)～(9).

式中:yi为样本值;^yi为拟合值.

图2 地震易损伤参数简化计算流程Fig.2 Flow chart of simplified calculation for Seismic vul n erability parameters

3.2.1 场地汇总下中位值的回归

将墩柱类型、上部支承结构类型和新旧规范纳为定性变量，假定每一个定性预测变量只有两水平，并用－1和1表示［23］.考虑不同桥梁分类对地震易损性函数中位值大小的影响，通过最小二乘法进行多元回归分析，得出场地汇总下的地震易损性函数中位值的简化计算公式，如式(10)所示.

式中:ε0、εe、εef为待定参数.进一步对回归方程中的变量进行显著性检验，设定95%的置信区间，将显著性水平大于0.05的变量判定为不显著，将其逐个删除，刷选出显著性的变量进行回归.

最终场地汇总下各损伤状态的地震易损性函数中位值的简化计算公式如式(11)～(14).

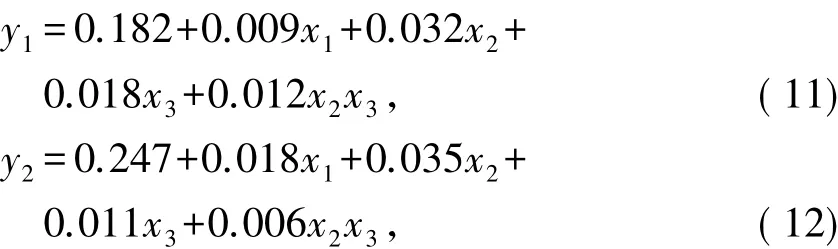
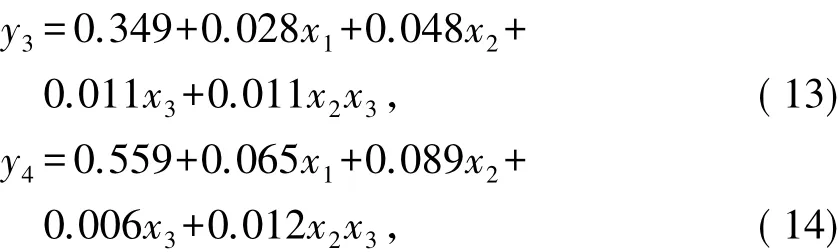
式中:yj为场地汇总下地震易损性模型的中位值，j=1，2，3，4分别表示轻微破坏、中等破坏、严重破坏、完全破坏;x1为规范类型、x2为墩柱类型、x3为上部结构类型，x1、x2、x3取值依据表5所示.通过式(11)～(14)，在已知规范类型、墩柱类型及上部支承类型的条件下，可以快速计算出场地汇总下不同损伤状态的桥梁易损性函数中位值，提高了易损性模型分析的时效性.

3.2.2 场地汇总与各类场地之间的关系

本小节以计算得到的桥梁类型汇总下的地震易损性函数中位值为基准，用最小二乘法建立正比例函数y=kx，得到不同场地类别下的地震易损性函数中位值.图3给出了不同场地类型下地震易损性函数中位值的实际值和线性回归的预测值.

表5 定性参数取值Tab.5 Value of qualitative parameters

由图3可知，通过对场地类型汇总下的地震易损性函数中位值乘以修正系数k，即可很好的回归出不同场地类别下的中位值.

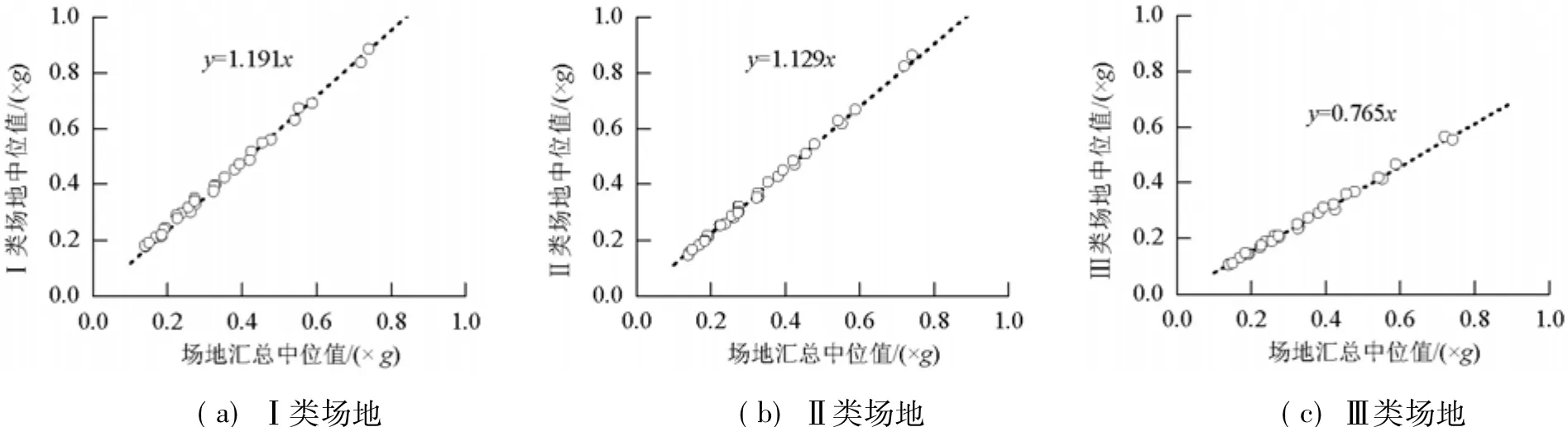
图3 不同场地类别下地震易损性函数中位值间的关系Fig.3 Correspondence of Seismic vulnerability median under the various sites

3.2.3 各类场地回归

本文综合考虑公式的简便程度与计算结果的误差之后，将前两节计算结果综合起来，在已知墩柱类型、上部支承结构类型和新旧规范的前提下，用4.2.1节回归得到的简化公式计算得到场地汇总下的4种损伤状态的地震易损性中位值，并乘以4.2.2节计算得到的修正系数，得出不同的桥梁分类与不同的场地类型下的地震易损性函数中位值，如式(15)～(16).

式中:不同损伤状态的 ε0、ε1、ε2、ε23等系数由式(11)～(14)给出;i=1，2，3分别代表场地汇总与一类、二类和三类场地.修正系数k由图3给出.

表6给出了不同参数下各中位值的误差估计.由表6可知，各损伤状态下EAug和ERms都较小，最大误差都小于6%，Emax稍大，其中轻微损伤的最大绝对误差最大，但都保证在11%以内.这表明本文提出的简化公式可以很好地拟合各参数下易损性函数的中位值.这对我国公路规则桥梁的地震易损性研究具有很大的实用性，可以帮助决策部门制定某个地区公路规则桥梁震后救援方案和加固维修计划.

表6 不同参数下各中位值的误差估计Tab.6 Error estimation of median under various parameters

3.3 地震易损性函数对数标准差的简化

图4 桥梁系统易损性对数标准差Fig.4 Logarithmic standard deviation of bridge system fragility

地震易损性函数对数标准差反应了桥梁地震响应数据的离散程度，在易损性曲线中体现为曲线的平缓程度.本文对每种损伤状态下的8类桥型和3种场地类型即24个样本点的对数标准差进行均值平滑处理，见图4.由图4可知，轻微破坏的对数标准差最大，完全破坏次之，中等破坏和严重破坏较小.由于对数标准差仅体现地震动强度的有效区间，并无相应符合的工程物理意义，且数据较为散乱，无法提出较为合理的简化方式，因此建议针对每一种损伤状态对其取均值，具体数值如表7所示.

表7 对数标准差建议值Tab.7 Proposed values of logarithmic standard deviation

4 结论

本文考虑桥梁和场地类型对桥梁系统地震易损性的影响，选择墩柱和支座作为桥梁的易损构件，基于大批量的非线性动力有限元分析，运用最小二乘法，回归得到各类桥梁的地震易损性模型.对生成的易损性模型展开参数化研究，并提出公路规则梁桥易损性模型的简化计算方法，得到结论如下:

(1)通过对不同桥梁类型的易损性模型比较，对于易损性函数中位值而言，不同墩柱形式对其影响较大，设计规范和上部结构形式影响相对较小.3种不同的场地类型下，双柱式中位值的数值都比相应的单柱式数值大17%以上、旧规范数值都比相应的新规范数值小7%～25%、简支梁数值都比相应的连续梁数值小8%以上.因此对于不同的桥梁形式，在相同地震动强度下，单柱式相对于双柱式更加易损，旧规范设计的桥梁相对于新规范设计的桥梁较易损，简支梁相对于连续梁较易损.

(2)对易损性函数对数标准差进行比较发现:对新旧规范连续梁桥，双柱式对数标准差小于单柱式，对于新旧规范简支梁桥，两者的对数标准差没有明确的大小关系;对于双柱式简支梁桥，旧规范对数标准差小于新规范，单柱式连续梁桥，旧规范对数标准差大于新规范，双柱式连续和单柱式简支梁桥对数标准差没确定的大小关系;对于双柱式新旧规范梁桥和单柱式新规范梁桥，简支梁桥对数标准差大于连续梁桥，单柱式旧规范简支梁桥对数标准差小于连续梁桥.

(3)本文对计算得到的易损性模型进行了参数研究，提出了适用于我国公路规则梁桥的中位值简化计算公式，并给出相应损伤状态的对数标准差建议值.通过与有限元计算结果进行比对，本文提出的简化计算公式均方误差和均方根误差都小于6%，最大绝对误差稍大，但都保证在11%以内.这说明本文提出的简化计算公式具有较高的准确性，方便易损性模型在工程实践中的应用与推广，能够为我国典型公路规则梁桥的地震风险评估及抗震加固决策提供参考依据.

［1］ SHINOZUKA M，FENG M Q，LEE J，et al.Statistical analysis of fragility curves［J］.Journal of Engineering Mechanics，2003，126(12):1224-1231.

［2］ SINGHAL A， KIREMIDJIAN A S. Method for probabilistic evaluation of seismic structural damage［J］.Structural Engineering，1996，122(12):1459-1467.

［3］ DUTTA A，MANDER J B.Seismic fragility analysis of highway bridges［C］∥ Proceedings of the INCEDEMCEER Center-to-CenterProjectWorkshopon Earthquake Engineering Frontiers in Transportation Systems.Blacksburg:State University of New York，1998:22-23.

［4］ 陈力波.汶川地区公路桥梁地震易损性分析研究［D］.成都:西南交通大学，2012.

［5］ HWANG H，JERNIGAN J B，LIN Y W.Evaluation of seismic damagetoMemphisbridgesand highway systems［J］.Journal of BridgeEngineering， 2000，5(4):322-330.

［6］ CHOI E， DESROCHESR，NIELSONB.Seismic fragility of typical bridges in moderate seismic zones［J］.Engineering Structures，2004，26(2):187-199.

［7］ GHOSH J，PADGETT J E.Aging considerations in the developmentof time- dependentseismic fragility curves［J］.Journal of Structural Engineering，2010，136(12):1497-1511.

［8］ 张菊辉，管仲国.规则连续梁桥地震易损性研究［J］.振动与冲击，2014，33(20):140-145.ZHANG Juhui，GUAN Zhongguo.Seismic vulnerability analysis of regular continuous girder bridges［J］.Journal of Vibration and shock，2014，33(20):140-145.

［9］ BUCKLE I G，FRIEDLAND I，MANDER J，et al.Seismic retrofitting manual for highway structures:part 1-bridges［R］.Washington D.C.:Federal Highway Administration，2006.

［10］ JAPAN Road Association.Specifications for highway bridges:partⅤ.seismic design［S］.Tokyo:Maruzen，2002.

［11］ 张国镇，蔡益超，宋裕祺，等.公路桥梁耐震能力评估及不强准则之研究［R］.台北:地震工程研究中心，2009.

［12］ 重庆交通科研设计院.JTG/TB02-01—2008公路桥梁抗震设计细则［S］.北京:人民交通出版社，2008.

［13］ 中华人民共和国交通部.JTJ 004—1989公路工程抗震设计规范［S］.北京:人民交通出版社，1989.

［14］ 中华人民共和国交通部.JT/T663—2006公路桥梁板式橡胶支座规格系列［S］.北京:人民交通出版社，2006.

［15］ MAZZONI S，MCKENNA F，FENVES G L.OpenSees command language manual［EB］.［2008-01-25］http://opensees.berkeley.edu/OpenSees/manuals/usermanual.

［16］ SPACONE E，CIAMPI V，FILIPPOU F C.Mixed formulation ofnonlinearbeam finite element［J］.Computers＆ Structures，1996，58(1):71-83.

［17］ TRIFUNAC M D，BRADY A G.A study on the duration ofstrong earthquake ground motion［J］.Bulletin of the Seismological Society of America，1975，65(3):581-626.

［18］ BERTERO V V.Strength and deformation capacities of buildings under extreme environments［J］.Structural engineering and mechanics，1977，53(1):211-215.

［19］ VAMVATSIKOS D.Incremental dynamic analysis［J］.Earthquake Engineering＆ Structural Dynamics，2002，31(3):491-514.

［20］ Federal Emergency Management Agency.HAZUS-MH MR4 earthquake model technical manual［M］.Washington D.C.:Springer，2003:1-93.

［21］ HWANG H，LIU J B，CHIU Y H.Seismic fragility analysis ofhighway bridges［R］. Memphis: The University of Memphi，2001.

［22］ ZHANG J，HUO Y.Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method［J］.Engineering Structures，2009，31(8):1648-1660.

［23］ JAMES G，WITTEN D，HASTIE T， et al.An introduction to statistical Learning with Applications in R［M］.Berlin:Springer，2013:41-72.