碰撞对山区高墩桥弹塑性动力响应的影响

李 晰， 贾宏宇， 李 倩， 康 锐， 陈志伟

(1.西南交通大学土木工程学院，四川成都610031;2.西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031)

在中国西南山区，为了跨越山高谷深的复杂地形，高等级公路及铁路系统中存在大量的高墩桥.高墩桥的主桥部分需要跨越河谷深沟，一般采用墩高较高的连续刚构体系或者连续梁体系，引桥部分一般采用墩高较矮的连续梁体系或者简支梁体系.因此，与常规的多联连续梁桥或者连续刚构桥相比，高墩桥最为显著的特点为墩高相差悬殊，属于不规则桥梁［1］，且其抗震设计已经超出中国现行桥梁抗震规范的适用范围［2］.

在以往的地震中，碰撞被认为是导致桥梁结构产生损伤及倒塌的一个重要原因，如在1989年的Loma Prieta地震［3］、1994 年的 Northridge地震、1995年的Kobe地震以及2008年的汶川地震中均有调查表明地震激励所引起的桥梁相邻结构之间的碰撞会使桥梁产生严重的损伤甚至倒塌［4-6］.已有研究表明［7-8］相邻结构动力特性的差别是引起桥梁结构产生碰撞的主要原因，并且美国Caltrans的抗震规范也建议对于多联桥梁结构，相邻联的周期比应大于0.7.然而由于受地形影响，高墩桥主桥和引桥墩高的显著不同会导致相邻两联桥梁结构的动力特性存在较大差别，使伸缩缝处的相邻梁体更容易发生碰撞.因此，相对于其他形式的桥梁结构，高墩桥在地震作用下的动力响应更容易受到碰撞的影响.

在过去的几十年里，碰撞对桥梁结构抗震性能的影响引起了很多学者的关注.大部分学者主要针对常规的多跨简支梁桥［9-10］和多联连续梁桥［11-12］或者连续刚构桥［13-15］进行了研究.但这些已有研究中有关碰撞对桥梁结构动力响应的影响有着不同的观点，有些研究认为碰撞对结构的受力状态不利，有些研究则认为碰撞会减小结构的响应.如Jankowski等［11］对连续梁桥进行了研究，指出碰撞力会显著增大墩底的内力，而Molhotra［12］则指出由于碰撞会耗散一定的能量，不会导致桥墩变形的增加.Chouw和 Hao［14］对多跨连续刚构桥进行了研究，指出碰撞在一定程度上会降低墩底的弯矩响应，DesRoches等［13］则指出碰撞会增大刚度较大结构的动力响应，而减小刚度较小结构的响应，特别是对于相邻结构动力特性相差较大的情形.因此，对于山区高墩桥这类非规则结构，有必要进一步研究碰撞对其地震响应的影响.

有关桥梁碰撞的参数研究表明，除了相邻结构刚度比之外，碰撞的模拟方法［16-17］、地震动的施加方式［18-20］、桥墩的非线性行为［10］等因素都会对桥梁结构的碰撞产生影响.但是，当前对高墩桥碰撞效应研究［21-22］没有或者简单考虑了碰撞中的能量耗散、桥梁的非线性行为等因素对桥梁碰撞所产生的影响.

鉴于此，本文以中国西南山区的实际高墩桥梁为原型，建立了两种典型桥跨结构的弹塑性动力分析模型，即连续刚构(主桥)-连续梁桥(引桥)和连续梁桥(主桥)-连续梁桥(引桥)，并考虑了碰撞的能量耗散、桥墩的非线性行为以及不同场地条件等因素.在此基础上，对比分析了碰撞对山区高墩桥弹塑性动力响应的影响，从而为山区高墩桥的减撞防撞设计提供相应的参考.

1 桥梁模型及动力特性

1.1 有限元模型建立

本文所选的原型桥梁为中国西南山区的一座实际高墩桥，该桥由两联组成，其中，主桥为三跨预应力混凝土刚构桥(跨径组合为88 m+168 m+88 m)，引桥为三跨变截面预应力混凝土连续梁桥(跨径组合为33 m+56 m+33 m)，主梁截面均为单箱单室箱形截面，顶板宽为12 m，底板宽为8 m，且梁高从跨中到支点处按二次抛物线变化.全桥共设5个桥墩，其中:1、2号墩为变截面空心矩形薄壁墩，墩高分别为75 m和103 m;3、4号墩为变截面空心圆角矩形薄壁墩，墩高分别为56 m和75 m，且3号墩为主桥和引桥的共用墩;5号墩为变截面实心圆角矩形重力式桥墩，墩高为19 m.具体桥型 布置见图1.

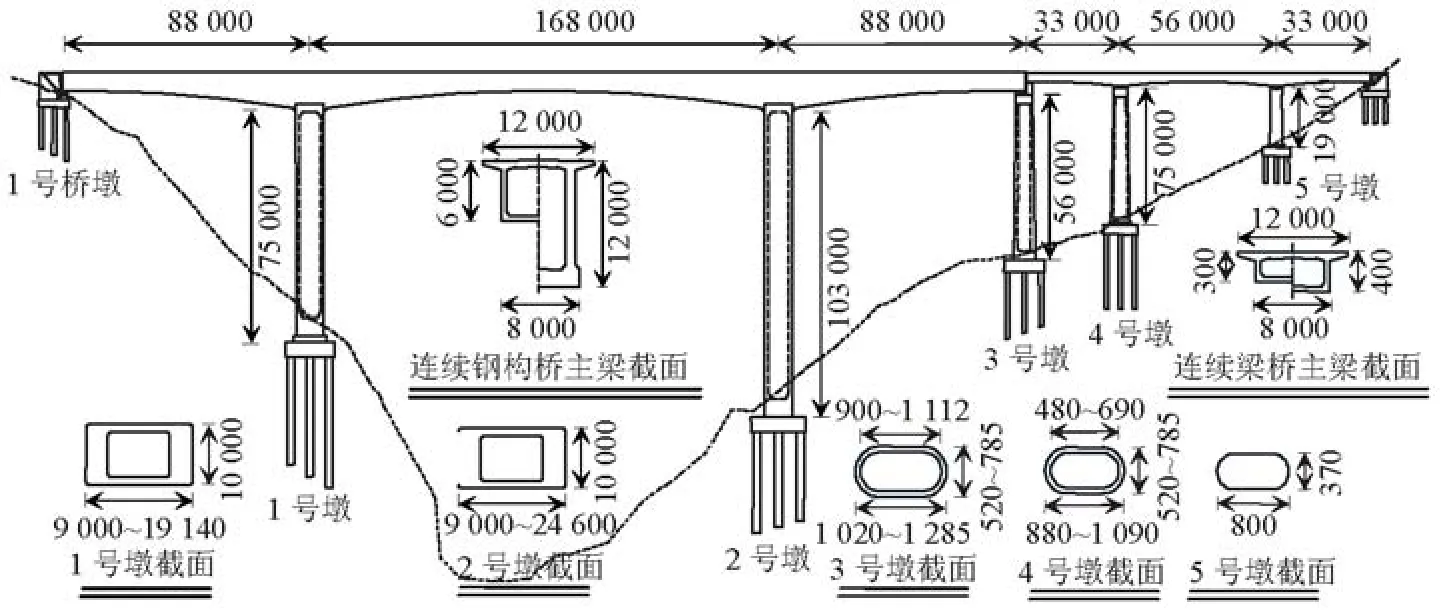
图1 全桥布置图Fig.1 Layout of the bridge

参照上述原型桥，以OpenSees作为分析平台分别建立了两种典型高墩桥体系的三维弹塑性动力分析模型，即连续刚构-连续梁桥体系(rigid bridge-continuous bridge，R-C)和连续梁桥-连续梁桥体系(continuous bridge-continuous bridge，CC)，有限元模型如图2所示.

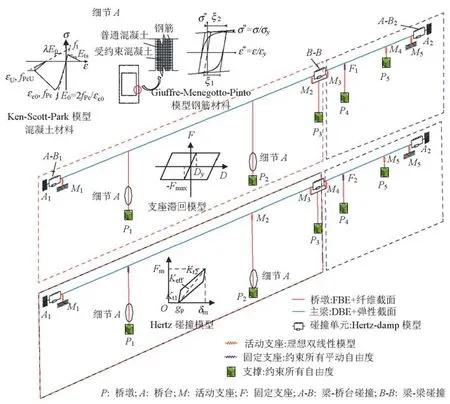
图2 三维有限元模型示意图Fig.2 Schematic view of 3-D FEA model

图2 中:ft为混凝土抗拉强度;Et为混凝土抗拉软化模量;fpc为混凝土28 d抗压强度;E0为混凝土初始弹性模量;εc0为混凝土达到抗拉强度时的应变;fpcU为混凝土残余强度;εU为混凝土残余强度对应的应变;λ为残余应变处的卸载斜拉与初始斜率的比值;σ和ε分别为钢筋的应力和应变;σy和εy分别为钢筋的屈服应力和应变;σ*和ε*分别为归一化的钢筋应力和应变;ζ1和ζ2为控制弹性段向塑性段过渡的参数;δm为最大入侵位移;gp为初始间隙;Fm为最大入侵位移所对应的碰撞力;Kt1和Kt2分别为初始刚度和应变硬化刚度;Keff为等效刚度;F和Fmax分别为支座滑动摩擦力和临界滑动摩擦力;D和Dy分别为支座位移和支座屈服位移.

高墩桥的主梁采用基于位移的梁柱单元(displacement-based beam-column element，DBE)结合弹性截面属性来模拟，并采用给单元两节点赋予不同截面属性的方法来考虑主梁截面高度沿纵向的变化.桥墩采用基于力的梁柱单元(forcebased beam-column element，FBE)结合纤维截面属性来模拟地震中可能出现的非线性行为.图2给出了桥墩纤维截面的划分示意，无约束混凝土和约束混凝土的材料特性基于kent-scott-park模型［23］，钢筋的材料 特 性基于 giuffré-menegottopinto model with isotropic strain hardening 模型［24］，支座采用连接单元来模拟，其滑动向的非线性行为采用双线性滞回材料来模拟.

此外，为了研究在地震中可能发生的梁-梁碰撞以及梁-桥台碰撞，采用Hertz-damp模型来模拟碰撞效应，并充分考虑了碰撞过程中的能量耗散以及碰撞刚度的变化，如图3(a).图中:kh为Hertzdamp理论模型的碰撞刚度，且相关参数依据《公路桥梁抗震设计细则》［2］的规定进行取值.

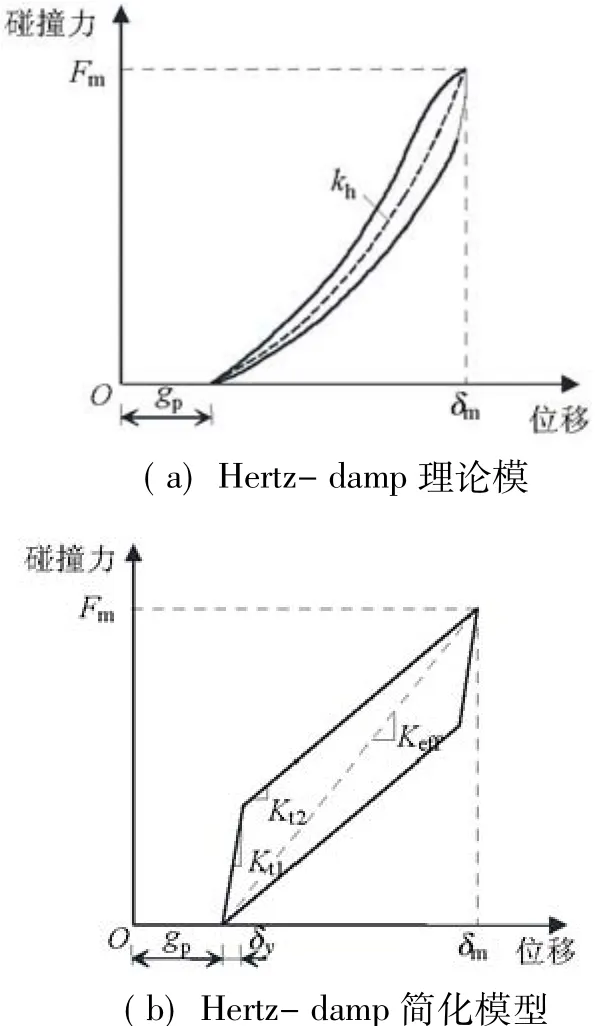
图3 Hertz-damp模型Fig.3 Hertz-damp model

为了方便在有限元软件中使用Hertz-damp模型，Muthukumar［25］给出了基于 Hertz-damp 理论模型的简化模型.该简化模型为双线性刚度接触模型，其碰撞力-位移关系如图3(b)所示.简化模型的参数主要包括Kt1，Kt2以及δy，这些主要参数都需要通过对Hertz-damp理论模型进行等效来确定.

对于本文的桥梁结构体系，Hertz-damp理论模型中关键参数的精确值需要通过试验或者基于实体模型的数值分析获得，但为了简化建模过程，通常也可以参照已有文献的经验值进行取值.因此，本文依据文献［25］有关Hertz-damper模型在混凝土桥梁结构中应用的研究结果，对碰撞模型的关键参数进行取值，并计算得到其它特征参数.相关参数的取值及计算结果如表1所示.表中:e为回归系数;n为Hertz系数;a为屈服参数.

表1 Hertz-damp简化模型特征参数Tab.1 Properties of Simplified Hertz-damp model

1.2 桥梁结构动力特性

对于本文所研究的高墩桥，主梁和桥墩(台)的连接分为3种形式，即墩梁固结、固定支座及单向滑动支座，因此主梁和桥墩(台)之间的横向位移均被约束，碰撞的主要形式为纵桥向的梁-梁碰撞和梁-桥台碰撞.鉴于此，本文主要研究在纵向地震激励下碰撞对桥梁结构动力响应的影响.桥梁结构纵向的模态信息如表2所示.从表2中可以看出，R-C体系中主桥和引桥的频率比为0.69，C-C体系中主桥和引桥的频率比为0.58，这说明高墩桥体系中相邻结构的动力特性相差较大，在地震激励下容易产生非一致振动.

表2 桥梁结构纵向模态信息Tab.2 Longitudinal modes of bridge structure

2 地震波激励与工况设置

本节所选的地震波分为人工地震波和天然地震记录两类，并考虑了不同的场地条件(硬场、中硬场和软场).为了考虑地震动的随机性，同一场地条件分别选取了3条人工合成地震波和3条天然地震记录.

对人工地震波，文献［26］所提供的方法来合成与目标谱相匹配的人工地震波.该方法基于所选的功率谱密度函数和包络函数对随机过程进行迭代修正来生成人工地震波.其中功率谱密度函数依据目标反应谱获得，包络函数采用Jennings提出的分段模型.本文将中国《公路桥梁抗震设计细则》［2］所规定的设计反应谱作为目标反应谱，不同场地条件下的目标谱如图4(a)所示，所生成的人工地震波与目标谱的匹配情况如图4(b)～(d)所示.

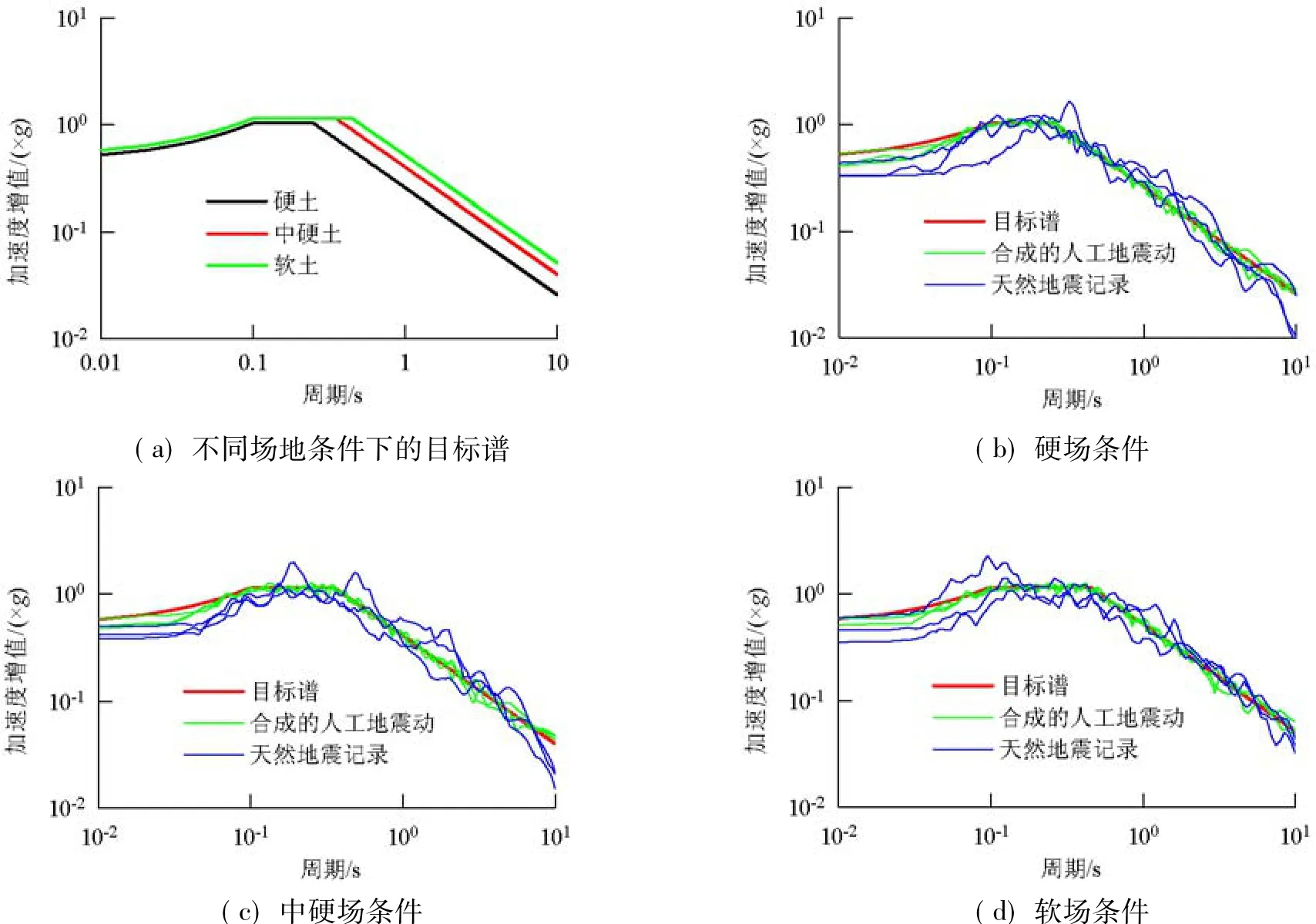
图4 目标反应谱与所选地震激励反应谱Fig.4 Target spectra and response spectra of selected ground motions

本文的天然地震记录均来自PEER 强震数据库［27］，使用者可通过确定目标反应谱及描述地震动的基本特性就可以挑选出一系列与目标反应谱相匹配的地震加速度时程.

对于所选地震动与目标反应谱的匹配程度，采用均方误差MSE来衡量，其基于地震记录的加速度谱与目标谱在感兴趣的周期范围内所对应的加速度谱值来计算，并且越小的MSE值表明所选地震动与目标谱有更好的匹配.表3给出了所选地震记录的详细信息.

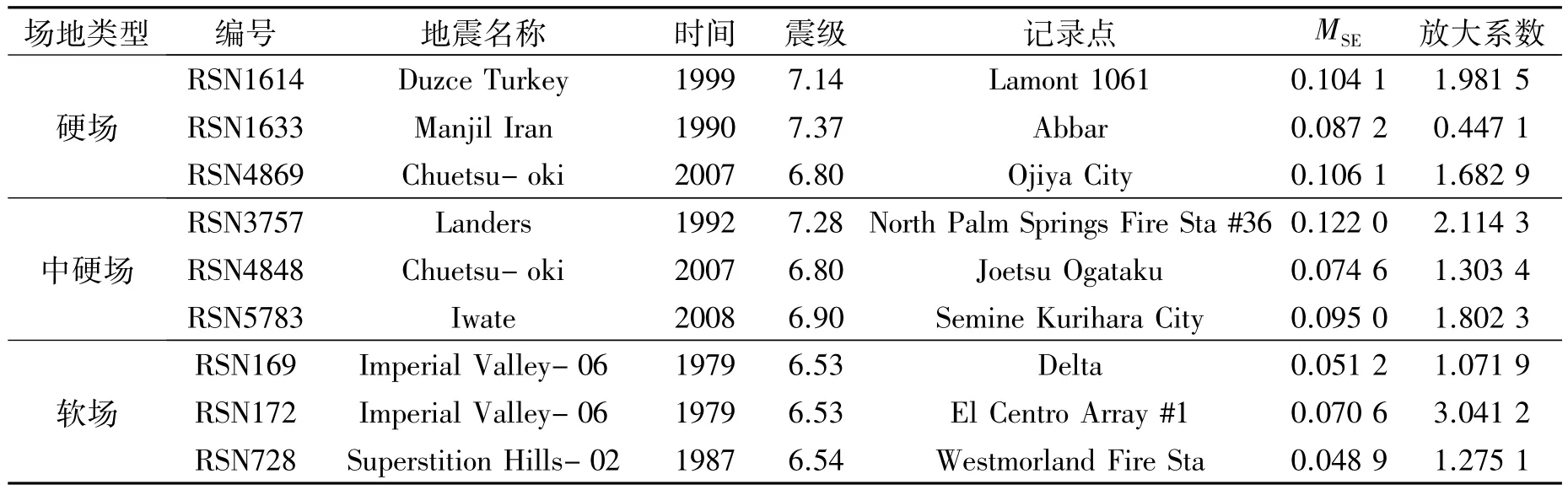
表3 所选地震动详细信息Tab.3 Detail of selected ground motions

从表3可以看出，所选地震动具有较低的MSE值(0.048 9～0.122 0)，说明其与目标谱匹配较好，这从图4(b)～(d)中也可以看出.各场地条件下典型的人工地震波加速度时程如图5(a)所示.各场地条件下典型的天然地震记录加速度时程曲线及加速度峰值PGA如图5(b)所示.

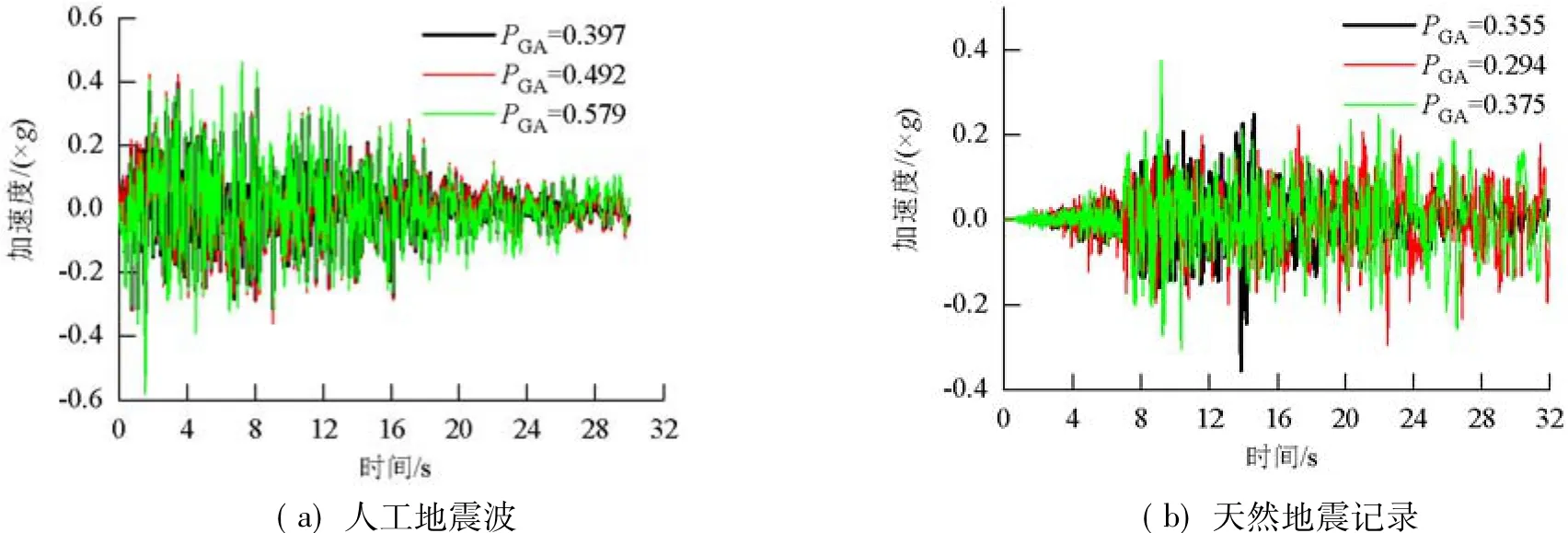
图5 各场地条件下典型地震波Fig.5 Typical ground motions for each site condition

由于本文主要研究碰撞对高墩桥弹塑性动力响应的影响，因此只在纵桥向施加了地震激励.基于所选地震动，共进行了36次计算，具体工况如表4所示.

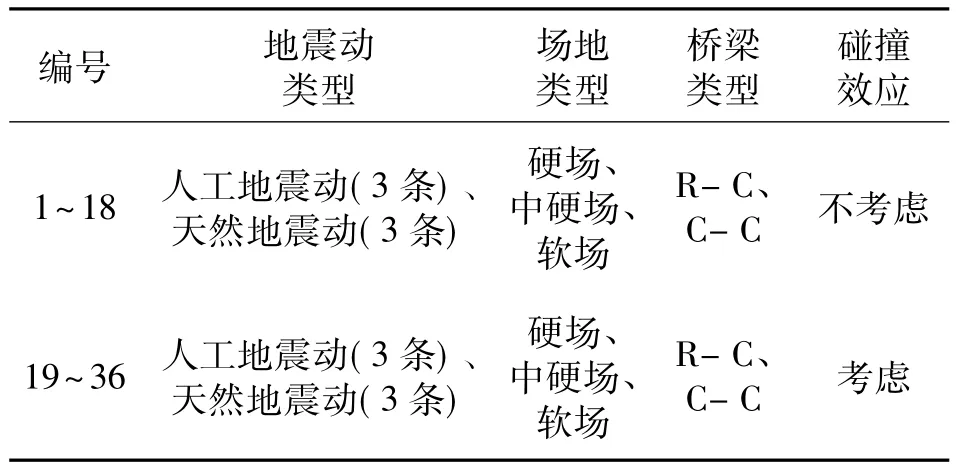
表4 工况列表Tab.4 Case details

3 结果分析

为了说明碰撞效应对结构响应的影响，本文定义了结构响应的改变率R=100(Rp－Rnp)/Rnp，其中:Rp为考虑碰撞效应时结构的响应;Rnp为不考虑碰撞效应时结构的响应.R为正值表示碰撞效应导致结构响应增大，反之则表示碰撞效应导致结构响应减小.

3.1 不同场地条件下碰撞对高墩桥动力响应的影响

图6、7分别给出了两种高墩桥结构体系在考虑碰撞和不考虑碰撞两种情形下的结构响应对比.从图6(a)和图7(a)可以看出，碰撞效应会对两种结构体系中的桥墩位移产生较为明显的影响，场地条件越差，碰撞效应对其的影响就越明显.从表5也可以看出:对于R-C结构体系和C-C结构体系，1号墩相对位移的最大改变率分别为6.36%与－8.77%;2号墩相对位移的最大改变率分别为6.86%和3.94%;3号墩相对位移的最大改变率分别为2.12%和－3.89%;4号墩相对位移的最大改变率分别为－10.50%和－12.81%;5号墩相对位移的最大改变率分别为－2.86%和－2.53%.

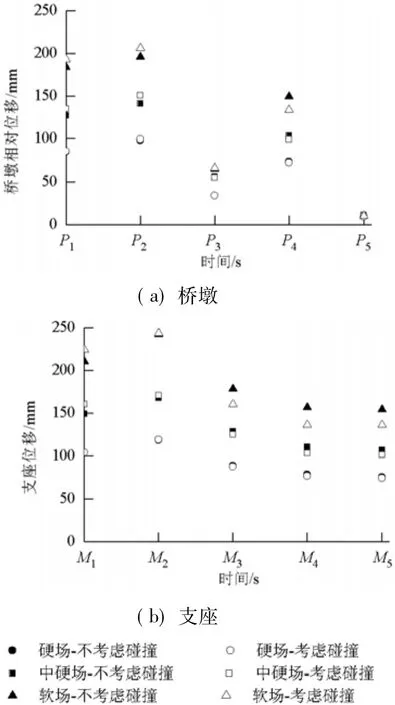
图6 R-C结构体系响应对比Fig.6 Response comparison of R-C structure system

从图6(b)和图7(b)可以看出，碰撞效应也会对两种体系结构中的支座位移产生较为显著的影响，场地条件越差，影响越为显著.对于R-C结构体系和C-C结构体系，支座位移的最大改变率分别为－13.17%和－15.86%，如表 6 所示.

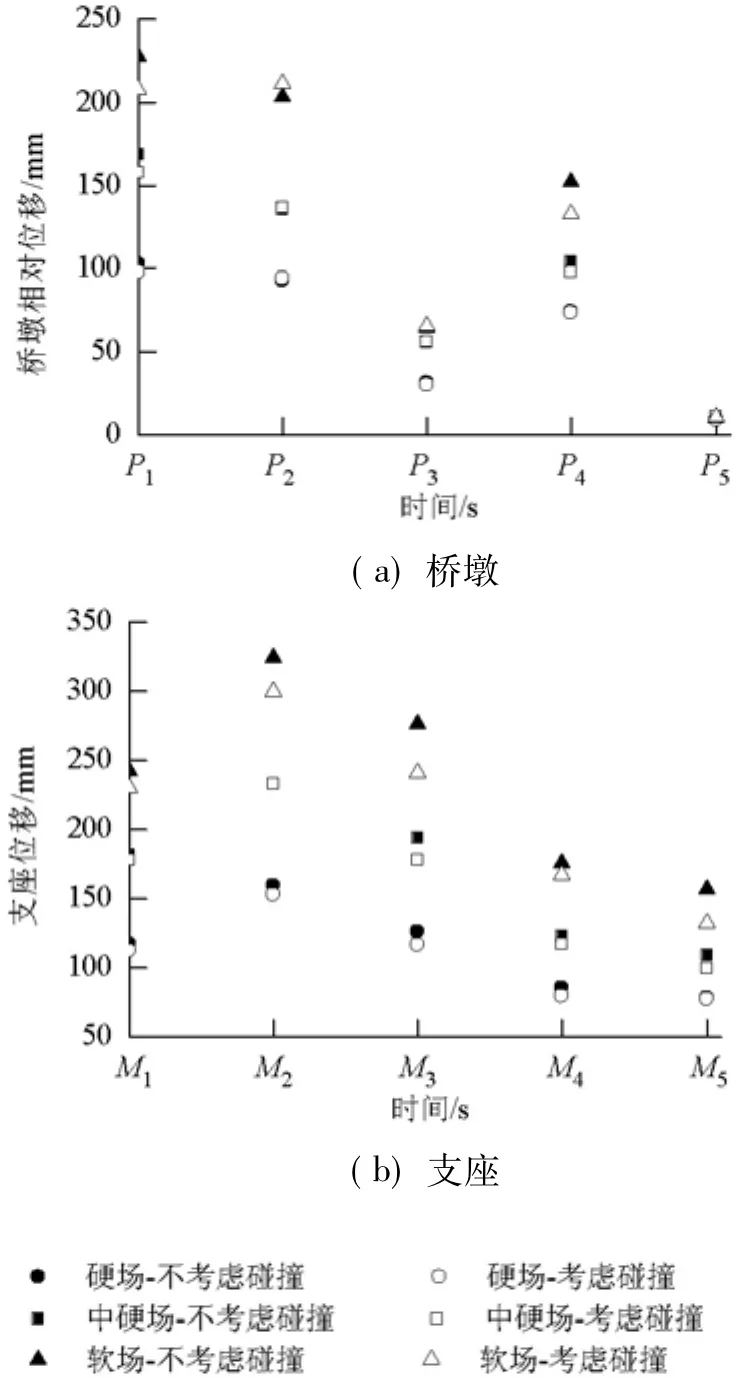
图7 C-C结构体系响应对比Fig.7 Response comparison of C-C structure system

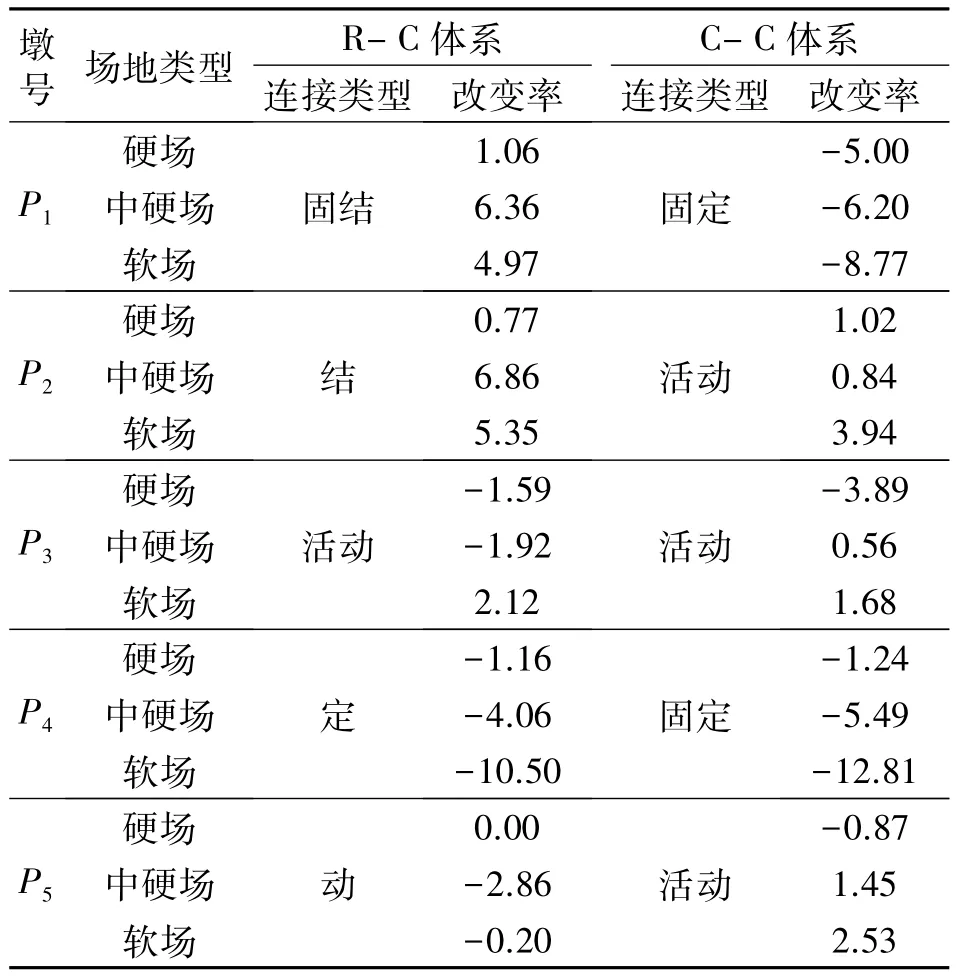
表5 桥墩相对位移改变率Tab.5 Change rate of pier displacement %

以上结果表明碰撞效应会对高墩桥结构的响应产生较为明显的影响在抗震设计中应引起重视，特别是在场地条件较差的情形，否则可能会错误的估计结构的响应.

从图6(a)、图7(a)及表5还可以看出，对于墩梁固结的桥墩(R-C结构体系中的1号墩、2号墩)，碰撞效应会较为明显的增大其相对位移，最大改变率为6.86%.对墩顶设置固定支座的桥墩(R-C结构体系中的4号墩以及C-C体系中的1号墩、4号墩)，碰撞效应会较为明显的降低其相对位移，最大改变率为－12.81%.对墩顶设置活动支座的桥墩(R-C结构系统中的3号墩、5号墩以及C-C体系中的2号墩、3号墩、5号墩)，碰撞效应不会对其产生较为明显的影响.产生这些现象的原因可以解释为:对墩梁固结以及墩底设置固定支座的桥墩，碰撞力可以通过这些连接传递至桥墩，因而会对桥墩的变形产生较为明显的影响;对墩顶设置活动支座的桥墩，无论碰撞力的大小，作用于墩顶位置的水平力均不会超过活动支座的滑动摩擦力，因此，碰撞力对此类桥墩的变形影响较小.这些现象说明碰撞效应对桥墩相对位移的影响大小及程度与桥墩同主梁的连接方式有较为密切的关系.在对高墩桥进行抗震设计时有必要对支座的类型及布置方式进行优化.

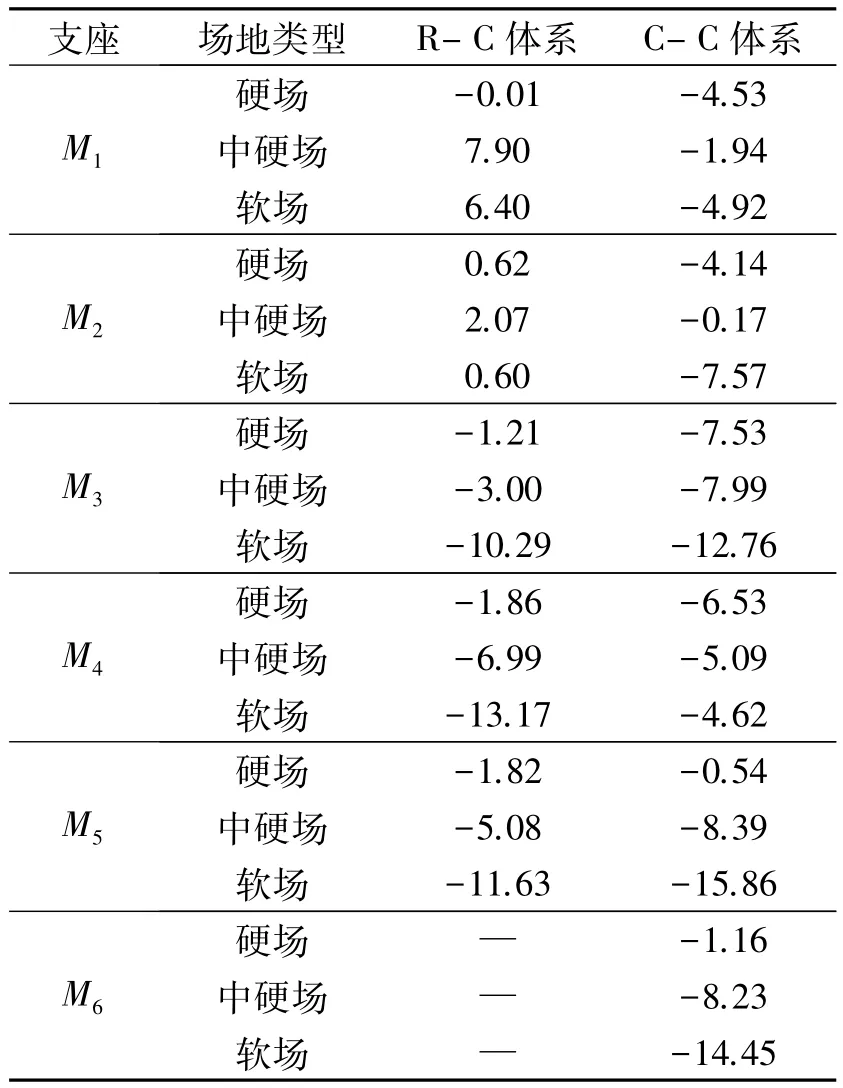
表6 支座位移改变率Tab.6 Change rate of bearings %

3.2 碰撞对不同结构体系高墩桥影响的差异

对比图6(a)和图7(a)可以看出，碰撞效应较为明显地增大了R-C结构体系主桥部分的桥墩相对位移(1号墩、2号墩)，而较为明显地降低了C-C结构体系主桥部分的桥墩相对位移(1号墩)，产生这种现象的原因可以依据结构的响应时程来解释.

图8分别给出了R-C结构体系和C-C结构体系的桥墩位移时程和碰撞力时程.

为了方便解释，将不考虑碰撞时的桥墩位移D，而考虑碰撞时的桥墩位移Dp.从图8(a)和(b)可以看出，当主梁与桥台发生碰撞时，由于碰撞的限制作用使指向桥台方向的主桥桥墩位移Dp要明显小于D，但在碰撞力和地震动的联合作用下，相反方向的桥墩位移可能会增大.如果下一次碰撞(梁与梁碰撞)发生在桥墩位移Dp小于D时，碰撞将会阻碍Dp继续增大，表现为碰撞作用降低了桥墩的位移(如图8(a)).如果下一次碰撞发生在Dp大于D时，虽然碰撞依然会限制桥墩位移继续增大，但此时桥墩位移Dp已经超过D，其表现为碰撞作用增大了桥墩位移(如图8(b)).这是因为碰撞会限制结构当前方向的变形，但同时可能联合地震作用增大相反方向的结构变形，此时碰撞对结构峰值位移的影响主要取决于第2次碰撞发生的时间.对比图8(a)和(b)可以看出，由于C-C结构体系中相邻结构的动力特性差异更大(如表5)，其发生梁-梁碰撞的概率要明显大于R-C结构体系，使碰撞的限制作用更容易在桥墩位移Dp小于D时发生，从而导致在考虑碰撞效应后，R-C结构体系的响应表现为增大而C-C结构体系的响应表现为减小.

表7给出了两种结构体系中各碰撞位置处的最大碰撞力以及发生碰撞次数，其中，碰撞次数是指结构在6条地震波作用下(6个工况)引起结构发生碰撞的工况数.

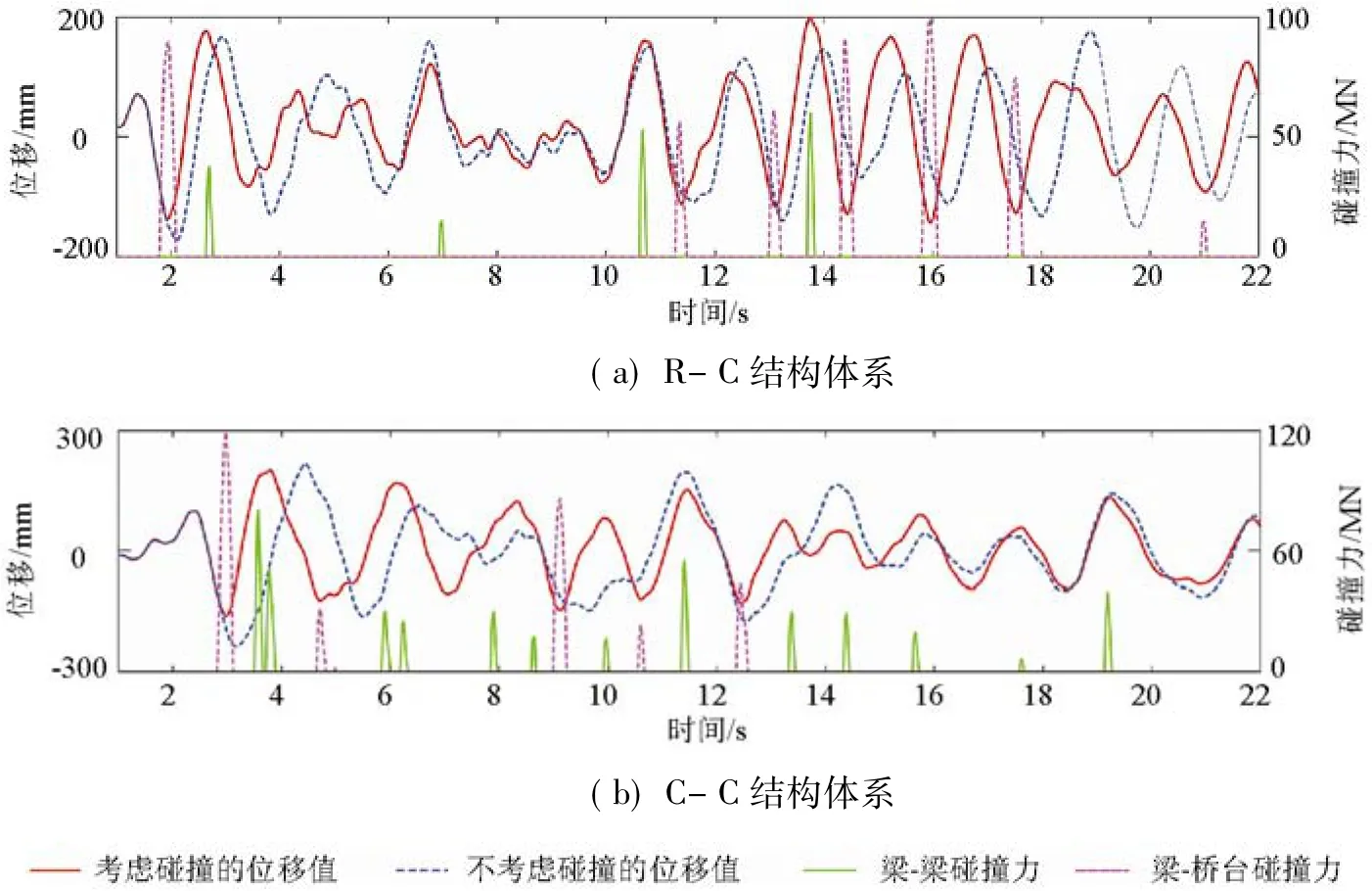
图8 桥墩相对位移及碰撞力时程对比图Fig.8 Comparison of piers relative displacements and pounding forces

从表7可以看出，C-C结构体系的碰撞次数较多，但其碰撞力要小于R-C结构体系.这可以解释为:由于碰撞次数较多，碰撞对C-C结构体系变形的限制作用更为明显，同时在碰撞过程中发生的能量耗散也更多，使C-C结构体系在发生碰撞时的碰撞力降低.

以上这些现象均说明虽然减小相邻结构的动力特性差异可以降低碰撞发生的概率，但有可能提高碰撞的强度及其对结构响应的放大的作用，从而对结构产生不利影响.因此在确定高墩桥结构体系的相邻结构周期比时，不能只考虑相邻结构动力特性差异对碰撞概率的影响，还应考虑其对碰撞效应的影响，避免出现碰撞次数减小而碰撞强度及结构响应增大的情况.

从表7还可以看出，对于梁-梁碰撞(B-B)，C-C结构体系的发生次数要明显高于R-C结构体系，这是由于C-C结构体系相邻结构的刚度差别要大于R-C结构体系，从而使其相邻结构更容易产生不同步振动.而对于梁-桥台碰撞(A-B1和A-B2)，两种结构体系的碰撞次数在同种场地条件下基本相同，这是因为桥台被假设为固定点，梁与桥台是否碰撞只取决于其自身结构振动幅值的大小.此外，还可以发现场地条件越差，两种结构体系发生碰撞的次数就越多，且碰撞力越大，这是因为场地条件会对地震动的幅值产生较为明显的影响.这些现象表明:对梁-桥台碰撞，其主要受地震动作用大小的影响，对梁-梁碰撞，不但与地震动的大小有关，还与相邻结构的动力特性相关，因此在进行减撞防撞设计时，应针对不同的碰撞位置采取不同的措施.

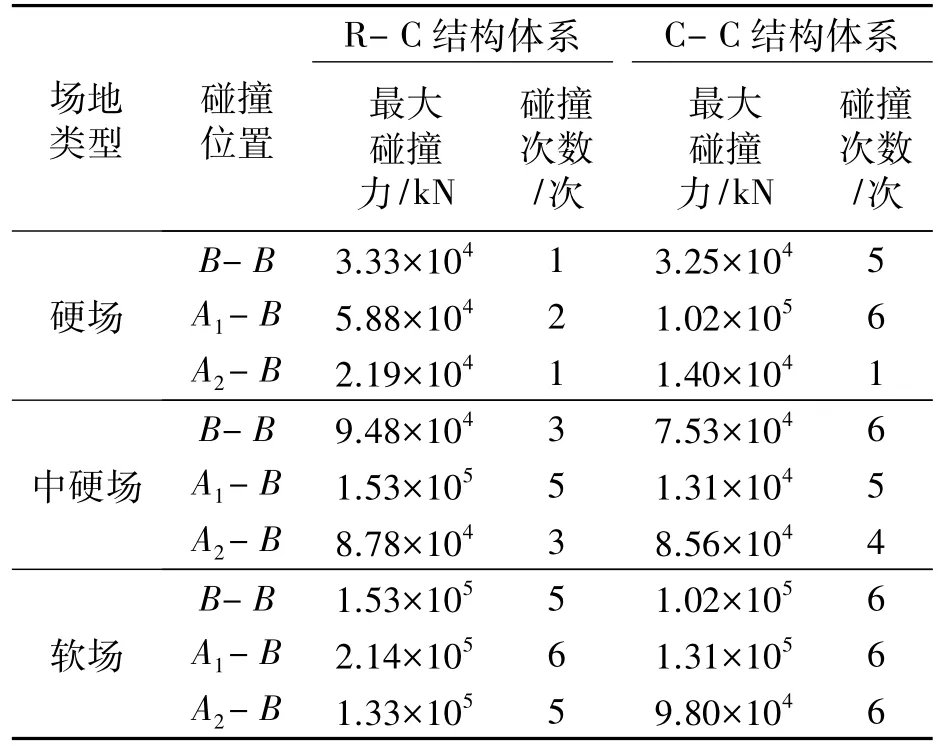
表7 最大碰撞力及碰撞次数Tab.7 Details of maximum pounding force and pounding frequency

4 结论

在充分考虑碰撞的刚度变化、能量耗散以及桥墩非线性行为的基础上，以两类典型的高墩桥结构体系为例，研究了碰撞对高墩桥动力响应的影响.得出如下结论:

(1)与不考虑碰撞的情形相比较，碰撞会对高墩桥结构的弹塑性动力响应产生较为明显的影响，特别是结构所处场地较差时，其最大改变率为15.86%.在抗震设计中应充分考虑碰撞效应带来的影响，否则会错误的估计结构的响应.

(2)桥墩与主梁的连接方式会改变碰撞效应对桥墩变形的影响大小和程度，即碰撞会对墩梁固结以及墩顶设置固定支座的桥墩产生较大影响而不会对墩顶设置滑动支座的桥墩产生明显影响.在进行高墩桥的减撞防撞设计时应考虑桥墩与主梁的连接方式对碰撞效应的影响，从而对支座的类型及布置形式进行优化.

(3)随着相邻结构动力特性差异的增大，其发生碰撞的概率也会增大，但由于碰撞对桥墩变形的限制作用，反而会降低桥墩的动力响应.因此在确定高墩桥结构体系的相邻结构周期比时，不但要考虑相邻结构动力特性差异对碰撞概率的影响，还应考虑其对碰撞效应的影响，即碰撞力的大小以及碰撞对结构响应的放大和缩小作用，从而避免出现碰撞次数减小而碰撞强度及结构响应增大的情况.

(4)梁-桥台碰撞主要受地震动作用大小的影响，而地震动的强度和相邻结构动力特性的差异都会对梁-梁碰撞产生影响，在对高墩桥进行减撞防撞设计时，应针对不同的碰撞位置采取不同的措施.

［1］ 宋晓东，李建中.山区桥梁的抗震概念设计［J］.地震工程与工程振动，2004，24(1):92-96.Song Xiaodong，Li Jianzhong.Seismic conceptual design for mountain bridges［J］.Earthquake Engineering and Engineering Vibration ，2004，24(1):92-96.

［2］ 中华人民共和国交通运输部.JTG/T B02-01—2008公路桥梁抗震设计细则［S］.北京:重庆交通科研设计院，2008.

［3］ LEW H S.Performance of structures during the loma prieta earthquake of October 17，1989［M］.Washington D C:NIST SP 778，1990:5-7.

［4］ MOEHLE J P.Northridge earthquake of January 17 1994:Reconnaissance report，volume 1- highway bridge and traffic management［J］.Earthquake Spectra，1995，11(3):287-372.

［5］ BRUNEAU M.Performance of steel bridges during the 1995 Hyogoken-Nanbu(Kobe，Japan)earthquake-a North American perspective［J］. Engineering Structures，1998，20(12):1063-1078.

［6］ HAN Q，DU X，LIU J，et al.Seismic damage of highway bridges during the 2008 Wenchuan earthquake［J］. Earthquake Engineering and Engineering Vibration，2009，8(2):263-273.

［7］ 李建中，范立础.非规则梁桥纵向地震反应及碰撞效应［J］.土木工程学报，2005，38(1):84-90.Li Jianzhong，Fan Lichu.Longitudinal seismic response and pounding effects of girder bridges with unconventional configurations［J］. China Civil Engineering Journal，2005，38(1):84-90.

［8］ PRIESTLEY M N，SEIBLE F，CALVI G M.Seismic design and retrofit of bridges［M］.New Jersey:John Wiley＆ Sons，1996:155-264.

［9］ ZANARDO G，HAO H，MODENA C.Seismic response of multi-span simply supported bridges to a spatially varying earthquake ground motion［J］. Earthquake Engineering ＆ Structural Dynamics，2010，31(6):1325-1345.

［10］ WON J H，MHA H S，KIM S H.Effects of the earthquake-induced pounding upon pier motions in the multi-span simply supported steel girder bridge［J］.Engineering Structures，2015，93:1-12.

［11］ JANKOWSKI R，WILDE K，FUJINO Y.Pounding of superstructure segments in isolated elevated bridge during earthquakes［J］.Earthquake Engineering ＆Structural Dynamics，2015，27(5):487-502.

［12］ MALHOTRA P K.Dynamics of seismic pounding at expansion joints of concrete bridges［J］.Journal of Engineering Mechanics，1998，124(7):794-802.

［13］ DESROCHESR， MUTHUKUMAR S. Effectof pounding and restrainerson seismic response of multiple- frame bridges［J］. JournalofStructural Engineering，2002，128(7):860-869.

［14］ CHOUW N， HAO H.SignificanceofSSIand nonuniform near- faultground motionsin bridge responseⅠ:effect on response with conventional expansion joint［J］.Engineering Structures， 2008，30(1):141-153.

［15］ NAVA F， NOBILIC， FERLA G.Experimental investigation of inelastic bridge response under spatially varying excitationswith pounding［J］.Engineering Structures，2014，79(54):106-116.

［16］ MUTHUKUMAR S，DESROCHES R.A Hertz contact modelwith non- linear damping for pounding simulation［J］.Earthquake Engineering ＆ Structural Dynamics，2006，35(7):811-828.

［17］ GUO Anxin，CUI Lili，LI Hui.Impact stiffness of the Contact-Element models for the pounding analysis of highway bridges:experimental evaluation［J］.Journal of Earthquake Engineering，2012，16(8):1132-1160.

［18］ BI K，HAO H，CHOUW N.Influence of ground motion spatial variation，site condition and SSI on the required separation distances of bridge structures to avoid seismic pounding［J］.Earthquake Engineering ＆Structural Dynamics，2011，40(9):1027-1043.

［19］ 周光伟，李建中，陈昌萍，等.行波输入下连续梁桥纵向墩梁相对位移碰撞效应分析［J］.世界地震工程，2012，28(4):51-57.ZHOU Guangwei，LI Jianzhong，CHEN Changping，et al.Analysis of longitudinal pounding due to relative displacement between pier top and girder of continuous girder bridge under input of traveling wave［J］.World Earthquake Engineering，2012，28(4):51-57.

［20］ LI B， BIK， CHOUW N， etal.Experimental investigation ofspatiallyvarying effectofground motions on bridge pounding［J］. Earthquake Engineering ＆ Structural Dynamics，2012，41(14):1959-1976.

［21］ 高玉峰，蒲黔辉，李晓斌.考虑碰撞效应的双柱式高墩桥梁非线性地震反应特性研究［J］.公路交通科技，2011，28(4):36-45.GAO Yufeng，PU Qianhui，LI Xiaobin.Nonlinear seismic response characteristics of bridge with doublecolumn high-rise piers considering pounding effect［J］.Journal of Highway and Transportation Research and Development，2011，28(4):36-45.

［22］ 王军文，李建中，范立础.非规则梁桥横桥向地震碰撞反应分析［J］.振动与冲击，2010，29(6):25-30.WANG Junwen，LI Jianzhong，FAN Lichu.Analysis on pounding effect of irregular girder bridges under transverse earthquake［J］.Journal of Vibration and Shock，2010，29(6):25-30.

［23］ YASSIN M H M.Nonlinear analysis of prestressed concrete structures under monotonic and cycling loads［D］.Berkeley:University of California，1994.

［24］ FILIPPOU F C，POPOV E P，BERTERO V V.Effects ofbond deterioration on hysteretic behavior of reinforced concrete joints［R］.Berkeley:University of California，1983.

［25］ MUTHUKUMAR S.A contact element approach with hysteresis damping for the analysis and design of pounding in bridges［D］.Georgia:Georgia Institute of Technology，2003.

［26］ VANMARCKE E H，GASPARINI D A.Simulated earthquake motions compatible with prescribed response spectra［R］. Boston: Dept. of Civil Engineering，Massachusetts Inst.of Technology，1976.

［27］ PEER.Technical report for the PEER ground motion database web application［R］. Berkeley: Pacific Earthquake Engineering Research Center，2010.