新证据冲突衡量标准下的证据二次修正组合

曹 洁，冯 锋，王进花

（兰州理工大学 计算机通信学院，兰州730050）

D-S证据理论是信息融合技术得以实现的重要工具，产生于20世纪60年代人们对多值映射工作的研究[1]。相对于概率论，它对证据的融合无需先验知识，对信息的表达和处理更加有效，因而D-S证据理论被广泛地应用于信息融合领域中[2]。然而，在证据理论发展应用的过程中，也遇到了诸如“一票否决”、“鲁棒性差”、“信任度偏移”等问题。对此，研究人员从以下方法开展了研究：

第一类方法，Smarandache等人认为证据理论框架本身不合理，并对其进行修改，在超幂集的框架上构建了DSmT理论。该理论处理不确定信息非常适宜，但对框架的修改难度很大。

第二类方法，许多学者将问题归咎于Dempster组合规则归一化运算，认为将冲突信度按比例分配给其他非空焦元并不合理，因而提出对Dempster组合规则进行修改[3-6]。

第三类方法，部分学者首先对Dempster组合规则给予肯定，认为合成结果有悖常理应归咎于数据模型的不合理性，因而提出在组合规则不变的情况下对证据源模型进行修改的方法[7-10]。

证据之间冲突程度的衡量是处理冲突的关键，常常被人们忽视。目前，对于衡量证据之间的冲突，尚未有统一的方法[11]。算例表明，用经典冲突系数k表征冲突的大小，并不合理。文献[12-13]提出，将Pignistic概率距离和k组合，构成1个二元组用于表征证据之间的冲突程度，其效果优于仅仅使用冲突系数k，然而由于证据是嵌套子集，如果证据条数＞2，则不能有效地判断证据之间的冲突。文献[14-15]利用Jousselme距离和冲突系数k的简单平均来修正原始的冲突系数。文献[16]用冲突系数和自定义的证据距离来描述证据之间的冲突，但是当存在相同证据时却不能用这样的表达式来描述它们之间的冲突程度。

针对上述问题，在此基于三角模算子定义了证据之间的相似度，计算得到了证据距离，并结合定义的证据马氏距离及经典冲突系数k，提出一种比较合理地衡量证据冲突的冲突系数。由此得到待组合证据体相应的权重，采用序贯方式实现证据组合。

组合前利用折扣因子对待组合证据予以修正，经Dempster组合规则融合后，利用信任系数对组合结果进行第2次修正，然后参与后续证据的组合。该组合方法摒弃了对传统D-S证据理论模型框架的修改，使实现组合的难度大大降低。其实质是对待组合证据体进行了预处理，并改变了传统批量式的融合方式，并未对组合规则本身进行修正，保留了组合规则所满足的交换律和结合律性质。

1 D-S证据理论存在的问题分析

文献[17]给出了D-S证据理论的基本概念。虽然证据理论在信息融合、故障诊断、智能决策等系统中已获得广泛运用，但是在实际应用中也遇到了难题。在此举例说明Dempster组合规则存在的不足。

1.1 高冲突证据组合问题

当k=1时，不能用Dempster组合规则进行融合，而当k→1时，对高冲突证据进行融合，将会产生有悖常理的结果。

例 1假定辨识框架 Θ=｛a，b，c｝，系统 2个证据为

证据 1：m1（a）=0.99，m1（b）=0.01

证据 2：m2（b）=0.01，m2（c）=0.99

证据m1和m2以0.99的信度值分别最大支持焦元a和c，而支持b的信度值只有0.01，但合成结果为 m（a）=m（c）=1，m（b）=0，融合结果有悖常理。同时，如果证据完全冲突，合成公式的分母为0，组合规则完全失效。

1.2 传统冲突表示存在的问题

例 2 假定辨识框架 Θ=｛A，B，C，D，E｝，2 个证据的基本概率分配为

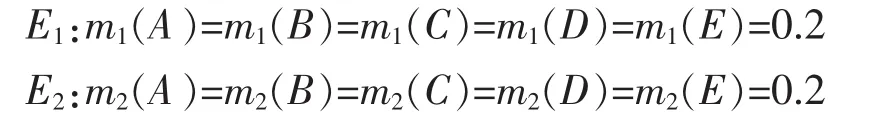
组合后的融合结果为

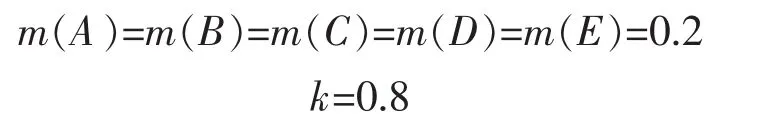
完全相同的证据体m1和m2冲突程度应为0。但是，计算得到系数k=0.8，说明描述证据冲突程度仅仅依靠传统冲突系数k，显然并不合理。而利用文献[14-16]所提冲突程度表达式在此计算冲突程度也不为0，据此可知其所提冲突系数并不全面。

1.3 引入三角模算子

分析经典冲突系数k及以上两例可知，仅利用焦元间的非包容性衡量证据间的冲突程度并不全面，证据之间的差异性也是衡量冲突程度必须考虑的重要因素。为了在描述证据冲突时利用证据之间的差异性，特引入三角模算子（triangular norm）[18]。

三角模算子是人工智能领域中的一种理论方法[19]，常依赖于模糊推理的思想，将单源决策映射到另一空间，通过比较来达到判决目的。三角模定义如下：

若映射 T（S1，S2），［0，1］*［0，1］→［0，1］，对∀a，b，c，d∈［0，1］，满足条件为

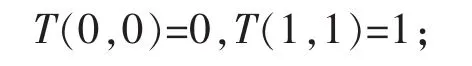
若 a≤b，c≤d 则 T（a，b）≤T（c，d）；

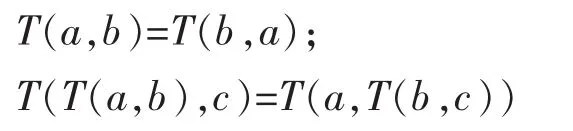
则映射T称为三角模算子或三角模。几种常见的三角模算子如下：

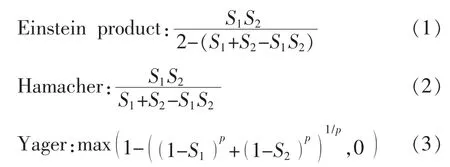
定义1假设m为识别框架Θ上的BPA函数，定义证据mi，mj之间的相似度为

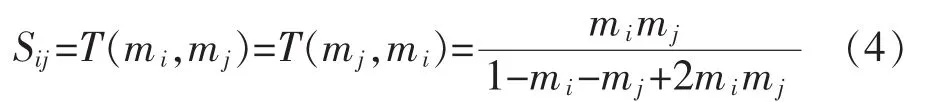
定义2证据mi和mj之间的证据距离定义为

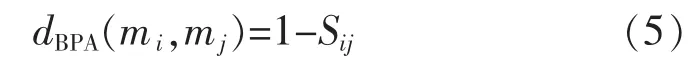
例3假定辨识框架Θ=｛a，b，c｝， 系统3个证据为

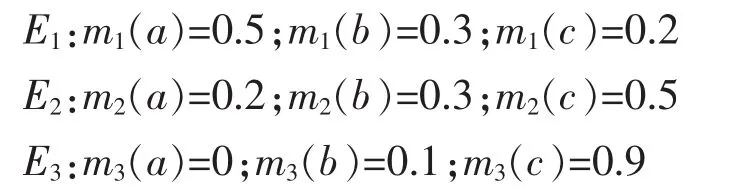
证据 E1支持 a，E2和 E3支持 c，一般推断 E2和E1的冲突要大于E2和E3，经计算得到k12=0.71，d12=0.32；k23=0.52，d23=0.38（kij为第 i个和第 j个证据的冲突系数；dij为第i个和第j个证据的距离）。故根据冲突系数判断E2和E1的冲突大于E2和E3，与分析一致，但按照距离来判断却会得到相反的结论，因此同样不能单纯利用证据距离来表征冲突程度。

2 基于新冲突系数的证据二次修正融合方法

2.1 新的冲突系数

为了更好地描述证据间的差异性，引入了马氏距离[20]（Mahalanobis distance）。 马氏距离有别于欧氏距离，由于考虑了各种特征之间的联系且独立于测量尺寸，用于计算2个未知样本集的相似度非常有效，能够避免变量相关性所造成的干扰。

第i，j两个样品之间的马氏距离为

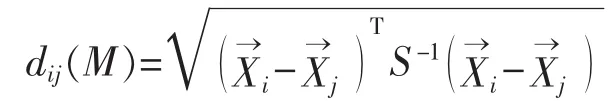
定义3假设m为识别空间U上的BPA函数，U→［0，1］，定义 mi和 mj之间的马氏距离为

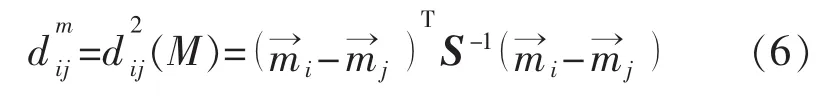
由上可知，冲突系数kij反映了证据之间的非包容性，而自定义证据距离 dBPA（mi，mj）及证据间的马氏距离能够反映证据间的差异性。鉴于此，为了充分利用两者在某些情况下的互补性，提出新的证据冲突程度的表达式为

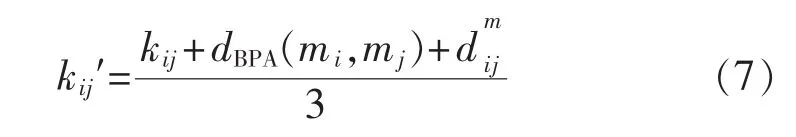
由式（7）可以看出，新的冲突系数 kij′为 kij，dBPA（mi，mj）和三者共同作用的结果。只有当三者均为0时，才说明证据间无冲突，同时也只有当三者都较大时，才能判定证据之间存在较大的冲突，有效地抑制了单一要素对证据冲突判定造成的偏差。

2.2 改进组合规则的实现

2.2.1 证据权重系数

证据的权重系数是证据的“价值”体现，与其他证据冲突较小的证据为“多数证据”，有利于最终组合结果的正确合成，权重系数较大；与其他证据冲突较大的证据为“少数证据”，它们会使最终合成结果有悖常理，应获得较小的权重系数。在此定义了第 i个与第 j（ j≠i）个证据的矛盾因子 kij′后，令

证据冲突程度方阵的每一个元素由证据间的冲突程度构成，于是n维冲突方阵为

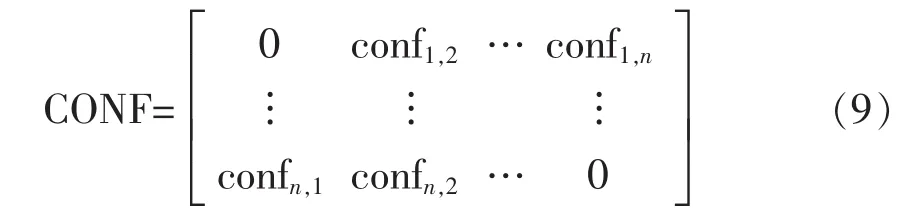
将冲突方阵的第i行或第i列相加，可得到第i个证据与其他证据的总冲突程度，即：

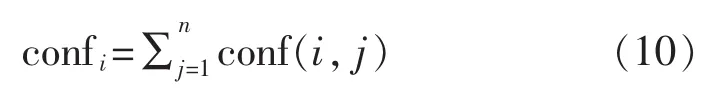
设有n个待组合的证据体mi，各自所对应的总冲突度为confi，每个证据体对应的权重为[21]

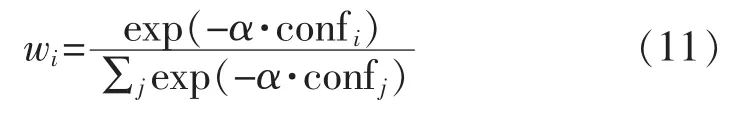
式中：α为负指数函数参数。

2.2.2 证据的二次修正

关键证据的权重系数最大，其权重系数为

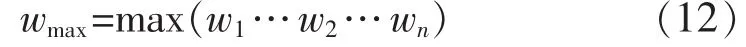
得到的各证据相对权重向量为

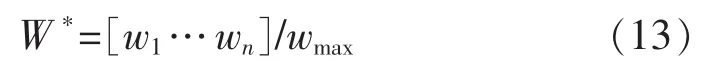
于是得到证据mass函数的“折扣因子”为

根据“折扣因子”对证据体进行第1次修正：

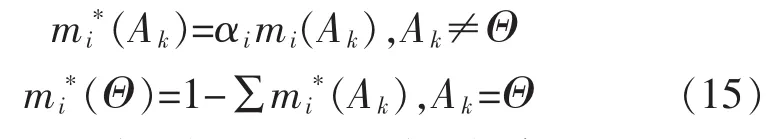
修正后的证据利用D-S规则进行合成。

定义4证据mi和mj之间融合的信任系数定义为

假设证据 mi和 mj融合后的结果为 mij（X），则第2次修正的结果为

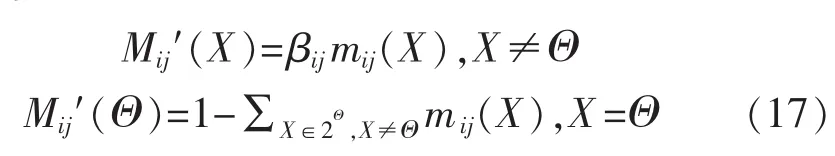
将修正的融合结果Mij′（X）和新证据重复上述融合与再修正，后续融合依此类推。融合过程类似于哈夫曼编码，由于采用序贯式融合，无需再对证据进行排序。 假设有 5 个证据 m1，m2，m3，m4，m5，计算得到对应的“折扣因子”为 α1，α2，α3，α4，α5，证据的二次修正过程如图1所示。

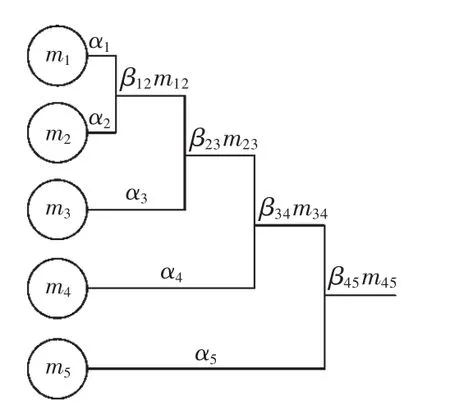
图1 证据的二次修正组合过程Fig.1 Secondary correction combination process of evidence

采用上述改进方法进行证据组合的步骤归纳如下：

步骤1融合系统（传感器）收集到n个证据，计算两两间的证据相似度；

步骤2计算两两间的证据距离，并得到新的冲突系数；

步骤3构造冲突方阵并分别计算各个证据的权重系数、折扣因子及衡量各步融合结果的信任系数；

步骤4采用序贯式进行证据二次修正组合，得到最终组合结果。

3 算例分析

3.1 试验1—新冲突衡量指标有效性验证

1）根据所提的冲突系数计算例1中所给证据体的冲突，由于证据m1最大支持焦元a，证据m2最大支持焦元c，2条证据之间存在较大冲突，由上述计算公式计算得到：

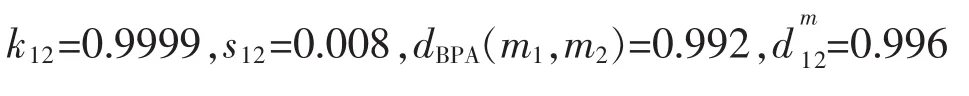
则新的冲突系数为

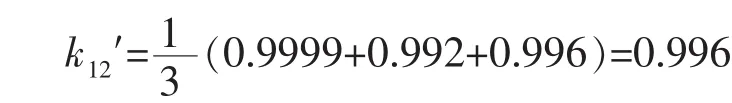
例1中，2组证据的冲突非常高，新冲突系数亦能准确反映出来。

2）根据所提出的冲突系数计算例2中所给证据体的冲突：

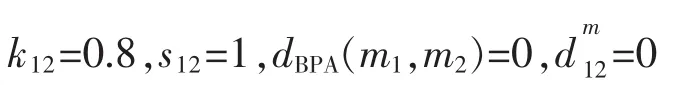
则新的冲突系数为

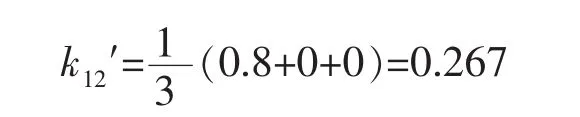
例2中，2组证据完全一致，因此证据间冲突程度应为0，所提方法计算结果并不为0，但相比经典冲突系数更加切合实际。由此可知所提出的冲突系数能够较好地反映证据间的冲突程度。

3.2 试验2—多源数据融合对比

以文献[23]给出的4个证据为例，将传统D-S组合方法及典型的几种修改方法的组合结果进行对比，从而验证所提方法的有效性。

假设辨识框架 Θ=｛A：民航机，B：轰炸机，C：战斗机｝，利用开发的软件仿真产生4组传感器数据，从而构成4个不同的证据体，即

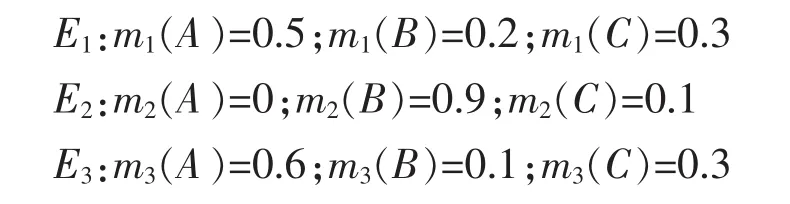
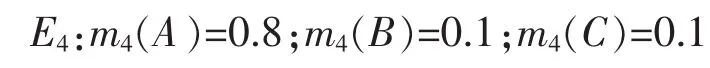
将这 4 个证据分别用 Dempster，Yager，Murphy，文献[3]，文献[22]，文献[23]和本文提出的二次修正组合方法进行融合，结果如表1所示。

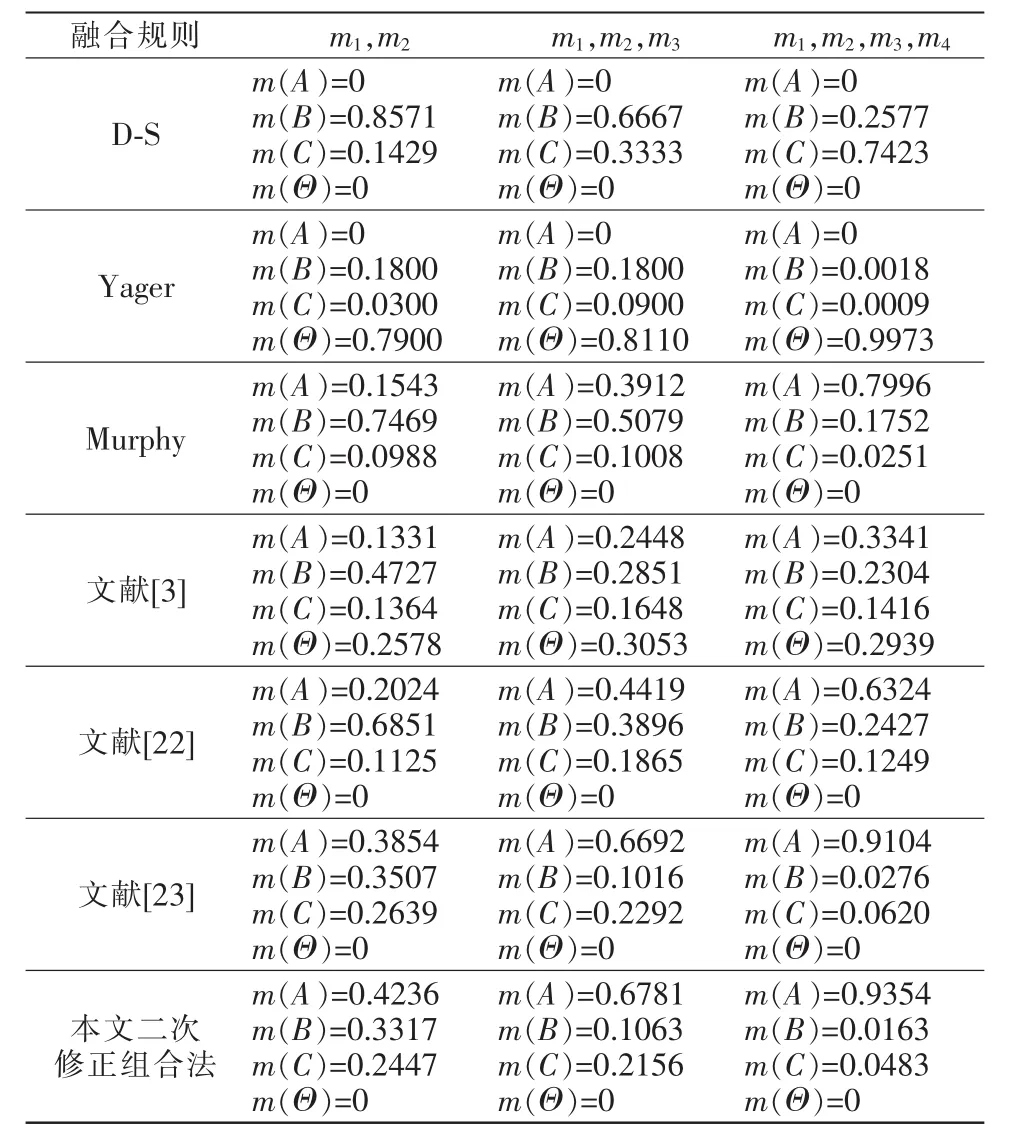
表1 多信息源融合结果Tab.1 Fusion results of multiple information sources

由表1可知，D-S组合规则无法有效地处理存在高冲突的证据，若存在支持度为0的证据体，则证据合成结果始终是0，而不依赖其他证据对该命题有多大的支持概率，即该组合规则存在“一票否决”的弊端而得出错误结论。

Yager的结果与D-S组合规则类似，并未克服“一票否决”的弊端，它将导致证据冲突的那部分信度值完全转移给Θ，证据数量的扩大也导致了未知项m（Θ）增大，从而增加了组合结果的不确定性。

Murphy平均方法的不足在于忽略了证据之间的相关性，虽然也能够正确识别目标A，由于它仅通过对证据简单平均来抵消证据2中 “坏值”0的影响，在系统收集到4个证据时才识别出目标A，所以收敛速度较慢。

本文提出的二次修正组合方法采用序贯方式实现证据组合，分别对组合前的证据及各步组合结果进行修正，有效地抑制了“坏证据”对系统最终融合结果的影响，提高了融合结果的准确性，避免了由于D-S融合方法改进而导致运算量的增加，使得整体的融合过程具有较小的计算量。

4 结语

信息融合系统，由于受到人为或自然环境等因素的干扰，使得收集到的证据之间常常存在较大冲突，这时传统的Dempster组合规则失效，无法得到令人满意且合理的融合结论，同时经典冲突系数对证据冲突的描述也并不合理。鉴于此，基于三角模算子及马氏距离，同时考虑证据间的非包容性和差异性，提出了新的冲突表示方法，从而有效地度量证据之间的冲突程度。然后，基于新的冲突表示方法提出了一种新的冲突信息融合方法，实现了融合过程的二次修正，在系统存在高冲突证据时仍能获得正确结论，且收敛速度快，计算量小。

[1]Pan G，Wu L L.An improved D-S evidence combination rule and its application[J].Systems Engineering，2014，32（6）：150-153.

[2]江涛.基于D-S证据理论的信息融合算法[J].计算机科学，2013，40（11A）：120-124.

[3]孙全，叶秀清，顾伟康.一种新的基于证据理论的合成公式[J].电子学报，2000，28（8）：117-119.

[4]Yager R.On the Dempster-Shafer framework and new combination rules[J].Information Sciences，1987，41（2）：93-137.

[5]张山鹰，潘泉，张洪才.证据推理冲突问题研究[J].航空学报，2001，22（4）：369-372.

[6]张捍东，王翠华，强克坤.基于焦元支持度的合成规则[J].控制理论与应用，2011，28（5）：741-744.

[7]Murphy C K.Combining belief functions when evidence onflicts[J].Information Fusion，2001，2（1）：91-101.

[8]邓勇，施文康，朱振福.一种有效处理冲突证据的组合方法[J].红外与毫米波学报，2004，23（1）：27-32.

[9]孟晨晨，肖建于.D-S证据组合规则下的修正系数的研究[J].计算机工程与应用，2016，52（19）：63-67.

[10]许将军.一种新的证据权重系数确定方法[J].计算机科学，2016，43（6A）：93-94.

[11]Wang Li，Bai Jing，Zhang Yi-ran.A New Method for Conflict Evidence Processing in D-S Theory[J].Science Technology and Engineering，2013，13（28）：8497-8500.

[12]Liu W R.Analyzing the degree of conflict among Belief functions[J].Artificial Intelligence，2006，170（11）：909-924.

[13]Lu R，Xu Q J，Zhang J，et al.Combination method of conflicting evidence based on mahalanobis distance[J].Communications Technology，2015，48（13）：278-282.

[14]蒋雯，彭进业，邓勇.一种新的证据冲突表示方法[J].系统工程与电子技术，2010，32（3）：562-565.

[15]蒋雯，张安，邓勇.基于新的证据冲突表示的信息融合方法研究[J].西北工业大学学报，2010，28（1）：27-32.

[16]曹洁，李晓瑶.一种新的证据融合方法及在目标跟踪中的应用[J].小型微型计算机系统，2015，36（4）：891-896.

[17]Liu Xi-liang，Chen Gua-ming.Improved evidence combination approach[J].Application Research of Computers，2013，30（9）：2668-2671.

[18]仇英辉，何霖.基于三角模算子的RPL协议路由优化算法[J].传感技术学报，2015，28（12）：1861-1866.

[19]王炫名，张晓林，景晓军.基于改进型的三角模准则的融合滤波算法[J].电子学报，2011，39（6）：1327-1330.

[20]鲁睿，徐启建，张杰，等.一种基于马氏距离的冲突证据组合方法[J].通信技术，2015，48（3）：278-282.

[21]韩德强，韩崇昭，邓勇，等.基于证据方差的加权证据组合[J].电子学报，2011，34（3A）：153-157.

[22]郭华伟，施文康，刘清坤，等.一种新的证据组合规则[J].上海交通大学学报，2006，40（11）：1895-1900.

[23]吕雪婷，贾瑞生，孙惠惠.证据冲突下D-S融合算法的改进[J].系统仿真学报，2013，25（3）：571-574.