液压传动型风力发电机组恒转速研究

党存禄，石 晶

（兰州理工大学 电气工程与信息工程学院，兰州 730050）

风力机是整个风电转换系统中的关键部件[1]。当前主流机型以变桨距变速机组为主，需要复杂的变桨距系统，机组的成本相对较高，系统可靠性降低。定桨距[2]风力机桨叶与轮毂直接刚性连接，当风速变化时，桨叶的桨距角不发生变化。定桨距型风力机利用失速性能良好的风力机桨叶，解决了机组在大风时的功率控制问题；叶尖扰流器成功地应用在风力发电机组上，解决了在突甩负载情况下的安全停机问题。且凭借其结构简单，可靠性高的优点，在近20年的风能开发利用中始终占据主导地位，被广泛应用。

液压传动风力发电机作为新一代风力发电设备[3]，采用液压柔性传动装置，解决塔架顶部设备、齿轮箱故障及维修问题，省去了传统机型中齿轮箱、变流器等装置，减少了塔架顶部设备的重量及装机成本。

据风电行业人士介绍，德国有400 kW的液压风电机组运行；美国、丹麦和挪威等国家正在研制阶段，未有产品报道；国内燕山大学的孔祥东教授团队针对定量泵-变量马达闭式系统[4]，在实验室完成系统工作机理研究，但主要是针对变桨距型液压风力机。

本文以上述研究为基础，采用定桨距型液压传动风电机组，在桨距角固定的情况下，研究影响转速的原因，要求发电机能够实现并网，对转速进行控制，使变量马达以恒速运行，同步并网。

1 定桨距型风力机

由于没有变桨功能，风力机从风中捕获的功率表述为[5]

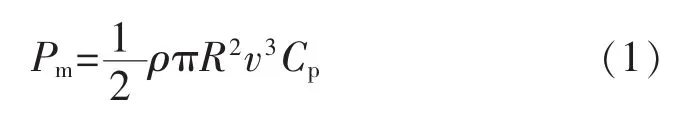
式中：Cp为风能利用系数，Cp仅由叶尖速比λ决定，λ＝ωR/v，ω 为风力机角速度；R 为叶片半径；v为风速；ρ为气流密度。

定桨距风力机输出功率P曲线规律如图1所示，图中ω*为风力机最优角速度，功率曲线只有一点具有最大功率Pmax，变化规律主要取决于Cp。

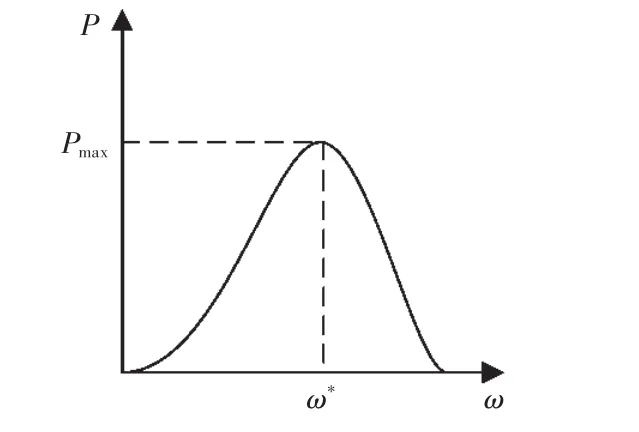
图1 风力机输出功率特性曲线Fig.1 Characteristic curve of output power of wind turbine

2 液压传动风力发电机组

2.1 液压系统工作原理

液压型风力发电机组主要包括主传动系统、偏航系统及刹车安全系统等。

图2为液压型风力发电机组的主传动系统示意。包括了风力机、定量泵-变量马达液压传动、同步发电机和发电控制系统等。定量泵与风力机连接安装在机舱里，风力机推动定量泵将风能转换为液压能。变量马达与同步发电机安装在地面上，液压能传输到变量马达处，驱动变量马达转动产生机械能，变量马达稳定输出转速，同步发电机并网[6]。

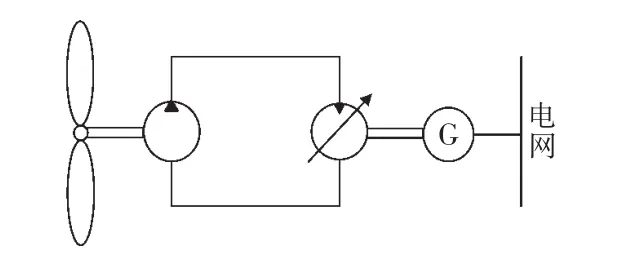
图2 液压型风力发电机组的主传动系统示意Fig.2 Schematic diagram of main drive system of hydraulic wind turbine

2.2 主传动数学模型

推导定量泵-变量马达系统传递函数时，原理如图3所示[7]。

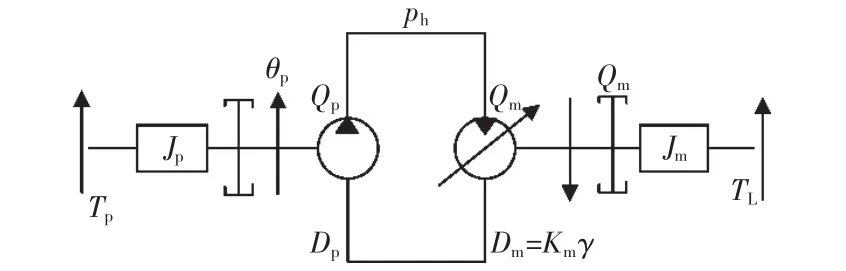
图3 主传动系统原理Fig.3 Schematic diagram of main drive system

定量泵流量方程为

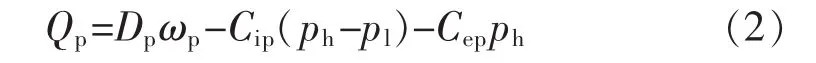
式中：Qp为定量泵流量（m3/s）；Dp为定量泵排量（m3/rad）；ωp为定量泵的转速（rad/s），Cip为定量泵内泄露系数（m3/（s·Pa））；Cep为定量泵外泄露系数（m3/（s·Pa））；ph为高压管路压力（Pa）；pl为低压管路压力（Pa）。

定量泵-变量马达高压腔流量连续方程为

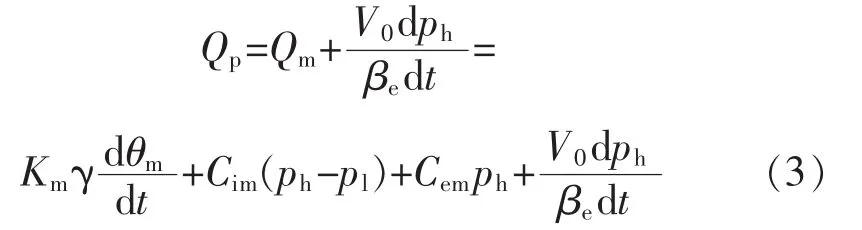
式中：Qm为变量马达流量（m3/s）；V0为高压管路的总容积（m3）； βe为油液综合体积弹性模量（Pa）；Qm为变量马达转角（rad）；Cim为变量马达内泄漏系数（m3/（s·Pa））；Cem为变量马达外泄漏系数 （m3/（s·Pa））；Qm为变量马达的转角（rad）。

变量马达排量方程为

式中：Dm为变量马达排量（m3/rad）；Km为变量马达排量梯度（m3/rad）；γ为变量马达摆角位置，取值区间［0，1］。

变量马达转速方程为

根据文献对变量马达转角θm的推导公式，可知变量马达转速对斜盘位置传递函数进行拉氏变换为

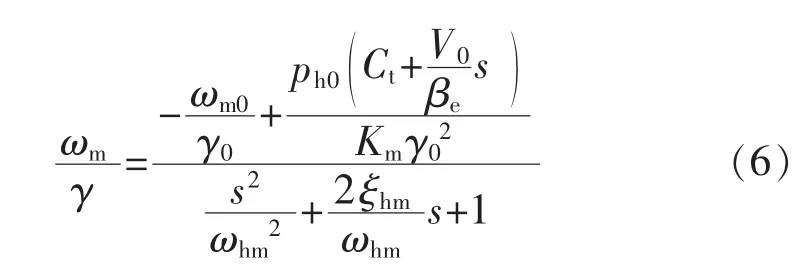
式中：ωhm为变量马达转速回路固有频率；ξhm为变量马达转速回路阻尼比。由于变量γ与乘积成非线性，将其线性化处理得：

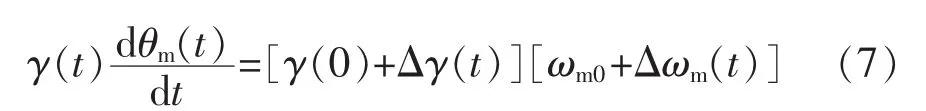
忽略高阶无穷小量得：

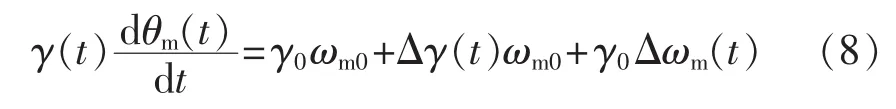
式中：γ0为变量马达摆角初始值；Δγ（t）为变量马达的摆角变化值；ωm0为变量马达初始的转速（rad/s）；Δωm（t）为变量马达的转速变化值（rad/s）。

变量马达输出功率传递函数为

2.3 液压传动风力发电机组控制原理

实现同步并网的要求[8]：①发电机端电压大小等于电网电压；②发电机频率与电网频率一致；③并网合闸时，发电机与电网回路电势为零；④发电机相序与电网相序一致；⑤发电机电压波形与电网电压波形相同。条件④和条件⑤在发电机设备选型和制造时已得到了保证。

由上述公式分析可知，风速大小影响了定量泵输出的流量和压力，风速越大，定量泵转速越高，流量和压力越大；定量泵和变量马达在一个闭环管路上，变量马达的开度由斜盘控制器控制，主要控制闭环管路中的流量，斜盘控制角越大，流量越大，变量马达转换的功率越大；变量马达和同步发电机同轴联接，将变量马达吸收的功率转换为电功率，吸收的越多，发电机输出的电功率越大；发电机输出电压大小由同步发电机的励磁电流决定；发电机的频率由转速决定。

3 液压型机组转速功率控制方法

由上述分析可知，当定量泵流量为常值时，系统压力不变，只有变量马达是变量，改变变量马达的排量，输出转速与马达排量成反比。定量泵转速随着风速不断变化输出不同流量时，变量马达产生不同转速。按照同步并网要求，需要频率一定，即需控制马达转速恒定不变，同步输出。由式（1）、式（2）知，通过改变马达的斜盘角度可实现。即输出转速高低由斜盘控制角决定，输出转速高，说明控制角偏大，需要调小，反之亦然。

泵转速变化时，对同一马达转速对应不同变量马达摆角γ，由式（6）知马达摆角γ与马达摆角初始值γ0和摆角变化值Δγ有关。不同的摆角γ变化时对转速和功率都有影响，采用图4所示液压型机组转速功率闭环控制方法[9]，通过反推理方式，间接用控制器控制斜盘角来控制变量马达转速和功率。

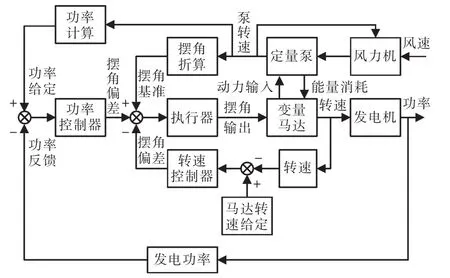
图4 液压型机组转速功率闭环控制方法Fig.4 Speed and power closed loop control method of hydraulic unit

在不断变化风速下，转速偏差经控制器得到摆角变化值Δγ形成马达摆角微调量，需要选定的马达初始值γ0接近工作要求，使其能在小范围内变化。此时若选定一固定的马达初始值γ0，可能造成Δγ变化过大，无法达到稳定调节。则需检测定量泵输入转速，按流量匹配原则计算所得初始值γ0，作为马达达到工作范围要求的初始输出转速摆角值，γ0-Δγ作为变量马达摆角控制值。

控制系统设计的核心内容是控制器的选择及参数的调节，在研究的液压传动型风力发电机组系统中存在非线性，采用PID调节所研究的是线性化后的系统模型，且动态性能和稳定性兼顾麻烦，存在矛盾。

因此，采用模糊PID控制方法[10]，结合传统PID控制器及模糊控制器优点进行优化控制。其利用模糊控制器灵活、快速的特点和PID控制器使用的方便性、鲁棒性等特点，使其可靠性和性价比更高，易于掌握。

4 控制系统仿真

通过某风力发电机组生产厂家提供真实风力机数据，实施600 kW风力机组主传动液压系统为研究对象。变量马达参数为排量1000 mL/r，最高压力42 MPa，马达输出转速初值为1500 r/min，采用相似理论确定计算其它实验数据。

根据数学模型和控制原理框图，利用Matlab/Simulink软件对系统进行仿真。定量泵取一个阶跃信号400～410 r/min，通过模糊PID不断调节参数，变量马达摆角仿真曲线如图5所示。

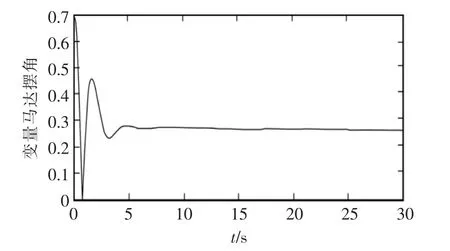
图5 变量马达摆角仿真曲线Fig.5 Simulation curve of swing angle of variable motor

通过控制器对马达摆角的闭环调节控制，变量马达转速的恒定输出仿真如图6所示。可知马达输出恒定转速能够使频率保持恒定，符合同步并网要求，即对速度影响因素分析控制方法完全可用。

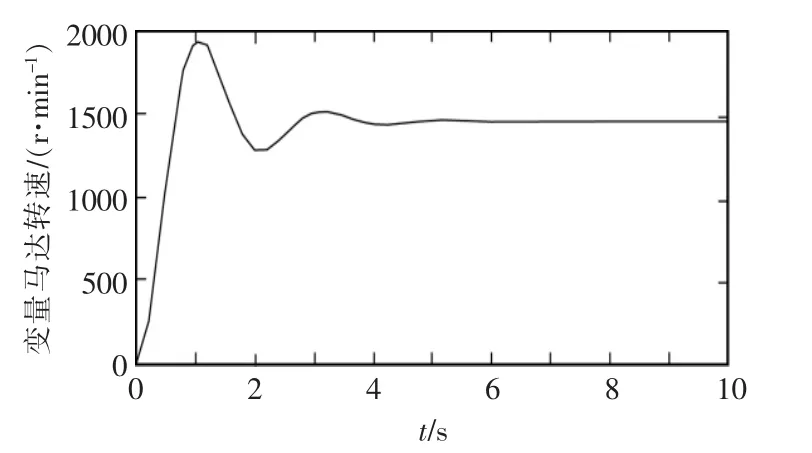
图6 变量马达转速仿真曲线Fig.6 Simulation curve of variable motor speed

5 结语

本文主要介绍了液压型风力发电机区别于传统风力机的优点。用液压柔性传动代替了机械刚性传动，减少了机组的机械故障率，降低了制造和维护成本。选用定桨距机组，机组在整个风速运行范围里实现与变桨距变速风力机相媲美的功率特性。针对变量马达恒速运行问题进行分析，通过间接控制马达摆角变化实现了对变量马达速度的恒定控制。由于试验设备不足，没有进行试验验证，存在不足。

[1]Abdul Motim Howlader，Naomitsu Urasaki，Kousuke Uchida，et al.Parameter identification of wind turbine for maximum powerpoint tracking control[J].Electric Power Components and Systems，2010（38）：603-614.

[2]胡祖荣.定桨距变速风力发电机组的变速控制技术研究 [D].江苏：南京航空航天大学，2010.

[3]Gruet R.The European Wind Energy Association.Wind energy and EU climate policy[R/OL].Print：www.artoos.be.2011：6-8.

[3]艾超，孔祥东，陈文婷，等.液压型风力发电机组主传动系统稳速控制研究[J].太阳能学报，2014，35（9）：1757-1763.

[4]赖日新.定桨距变速风力发电机组的控制技术研究及其仿真[D].江苏：南京航空航天大学，2009.

[5]Johannes Schmitz，Nils Vatheuer，Hubertus Murrenhoff.Hydrostatic drive train in wind energy plants[J].Drive Train Components and Power Electronics，2011：1-8.

[6]艾超，闫桂山.液压型风力发电机组最优功率追踪控制方法研究[J].动力工程学报，2015，35（2）：126-132.

[7]张刚.液压型风力发电机组主传动系统功率控制研究[D].河北：燕山大学，2012.

[8]艾超.液压型风力发电机组转速控制和功率控制研究[D].河北：燕山大学，2012.

[9]张高峰.液压传动型风力发电系统马达转速特性研究[D].辽宁：大连理工大学，2012.