砂性海床管道承载能力与入泥深度上限分析❋

张其一， 董小松

(1. 中国海洋大学工程学院, 山东 青岛 266100; 2. 山东省海洋工程重点试验室, 山东 青岛 266100)

海床上不要求埋设的海底管道，对其进行在位期间稳定性分析时，管道的入泥深度是一个非常重要的参数。因为管道的入泥深度直接影响到作用在管道上的水动力计算和管道周围土体的约束作用，而这些水动力效应和海床土体约束又是确定管道稳定性的重要因素。海底管道在自重和外部附加荷载作用下，都将不同程度地压缩管周土体发生局部或整体的不可恢复塑性变形或破坏，直到达到平衡状态为止。管道的入泥深度与海床地基的极限承载能力密切相关，为了探讨浅埋管道的入泥深度，首先需要确定圆形管道周围土体的极限承载能力。

目前，国内外学者与工程人员在计算海底管道入泥深度时，往往借鉴条形基础地基承载力计算公式，部分规范给出水下饱和软黏土海床上管道单位长度的极限承载能力为(2+π)SuB[1]，日本规范则采用3SuB作为软黏土海床上管道极限承载力计算公式[2]。天津大学闫澍旺教授利用极限平衡与极限分析原理，基于Prandtl塑性破坏模式，按照二维条形基础模式，推导了饱和软黏土海床上管道极限承载能力与入泥深度，为本文进一步深入研究砂性海床管道入泥深度提供了理论支持。

国外，Merifield et al利用有限元法详细研究了环境荷载作用下海管周围土体的变形规律与承载能力[3]。Randolph & White比较详细地研究了浅埋海管的极限承载能力[4]。Krost et al利用数值方法分析了管道周围土体中超孔隙水压力的消散规律[5]，计算结果往往都是同二维条形基础计算公式进行对比。海床上的圆形管道与条形基础的几何形状明显不同，地基土体的极限承载能力也必然存在较大差异，因而不能完全沿用条形基础的地基承载力公式。为了准确而合理地确定砂性海床上海底管道的极限承载能力，求得相应的入泥深度，有必要从理论上研究管道周围土体的变形规律与失稳模式。

事实上，能否准确求解海床上浅埋圆管的极限承载能力，取决于地基土体极限状态时的失稳模式。本文基于Hill塑性失稳模式[6]，根据圆周边界滑移线场混合边值方程，构建了浅埋圆管周围土体的运动许可速度场，利用虚功率原理分析了砂性海床上浅埋管道极限承载能力，并推导出了管道入泥深度计算公式，与常用的Terzaghi承载力计算公式进行了详细对比，验证了该方法的可行性。

1 浅埋圆形管道承载力与入泥深度上限分析

虚功率原理指出[7]：对于任意一组静力容许的应力场和任意一组机动容许的速度场，外力的虚功率等于物体内能耗散功率。而且上限定理指出：在所有运动许可变形场(速度场)所对应的极限荷载中，真实的极限荷载最小，换言之，由运动许可变形场所确定的极限荷载一定不小于真实极限荷载。

1.1 运动许可速度场的建立

根据极限分析上限定理，针对半径为R、入泥深度为h的浅埋圆管构造运动许可速度场[8]。做出如下假定：

(1) 考虑到三维问题运动许可速度场构建的复杂性[9]，本文取单位长度圆形管道为研究对象，将三维问题简化为二维平面应变问题，如图1所示；

(2) 圆形管道为完全刚性体，管道与海床土体之间为光滑接触；

(3) 海床土体为刚塑性体，满足相关联流动法则，且服从Mohr-Coulomb破坏准则与简单加载条件[10]；

(4) 管道周围海床土体破坏区分为两部分：螺旋面abc塑性剪切变形区、acd三角形Rankine被动区，如图2所示；图2(b)只绘出了管道右侧土体的塑性破坏区域，管道左侧土体破坏模式与右侧一致；

(5) 基础竖向初始速度为VP，基础底部土体b点剪切滑裂面上速度大小与方向如图2(a)所示；

(6) 为了简化推导，暂不考虑重力作用。

图1 海床浅埋圆形管道

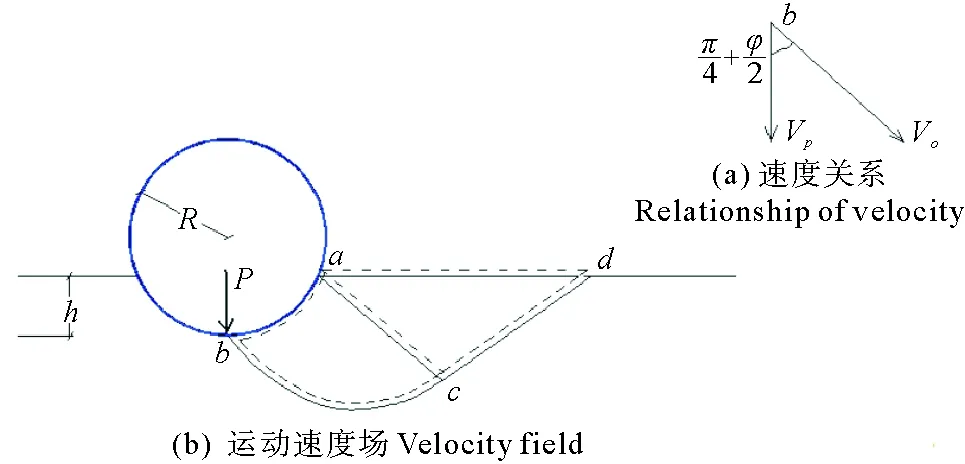
图2 运动许可速度场

1.2 上限分析

本文理论推导过程中，内能耗散率包括速度间断面上的能量耗散率、螺旋变形区能量耗散率，外功率为极限载荷作用下的虚功率。

1.2.1 运动速度场几何关系 基于图3所示对数螺旋线关系，b、e、c为螺旋线上的点，且oac三点共线，可求得旋转线中心点o的位置；当圆形管道入泥深度为h时，存在如下几何关系：

(1)

(2)

(3)

oe=ob·exp(θ·tanφ)，

(4)

其中，令

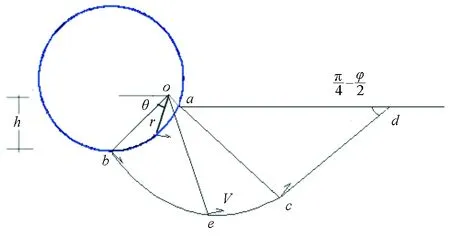
图3 运动速度场几何关系

1.2.2 滑动土体内能耗散率

(1) 管道下部塑性变形区abc能量耗散率

exp(2tanφ·θ)Vodθ，

(5)

令：

(6)

(7)

则可推得

Wabc=cVoR·M·f(h)·ctanφ-SuVo·

(8)

(2)bc螺旋弧间断面内能耗散率

exp(2tanφ·θ)dθ，

(9)

令

(10)

则上式可得到

[exp(2tanφ·θ*)-1]。

(11)

(3)cd被动区间断面内能耗散率

Wcd=cVoexp(tanφ·θ*)·

(12)

1.2.3 外力总功率 作用在圆形管道上的外部荷载P，在竖向速度VP情况下产生的外力功率为：

Wext=P·VP。

(13)

1.2.4 上限解答 由极限分析上限定理知，外力总功率等于内能耗散率。则浅埋圆形管道极限承载力P与管道入泥深度h满足如下能量守恒方程：

(14)

2 浅埋管道承载力与入泥深度

当圆管入泥深度超过半径R时，会导致管道周围土体向管壁回流，同时被动区出逸点d将消失于海床表面，此时运动许可速度场将比较复杂，随后文章将对这一特殊问题进行进一步讨论。所以，本文给出的管道承载能力与入泥深度上限解答，只适用于管道入泥深度不超过管道半径R的情况。

本文分别取半径R为0.25、0.5、0.75、1.0、1.25、1.5、1.75、2.0 m等8种工况，入泥深度h分别取h=0.1R、h=0.3R、h=0.5R、h=0.7R、h=0.9R等5种工况，海床砂性土力学参数为c=12kPa、γ′=800 N/m3，φ=15°、φ=20°以及φ=25°等三种情况。圆形管道周围海床土体极限承载能力Q部分计算结果如下表1、2和3所示，表中对土体极限承载能力进行了无量纲处理。

表1 不同工况下管道承载能力与入泥深度(φ=15°)

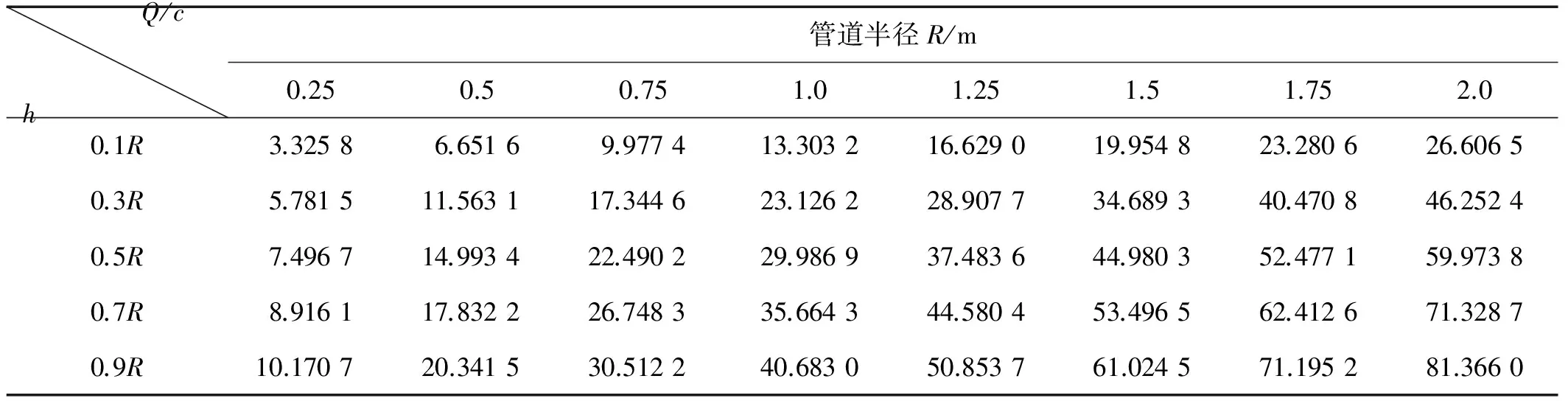
表2 不同工况下管道承载能力与入泥深度(φ=20°)

表3 不同工况下管道承载能力与入泥深度(φ=25°)

图4 本文上限解答与部分理论公式对比图(φ=15°)

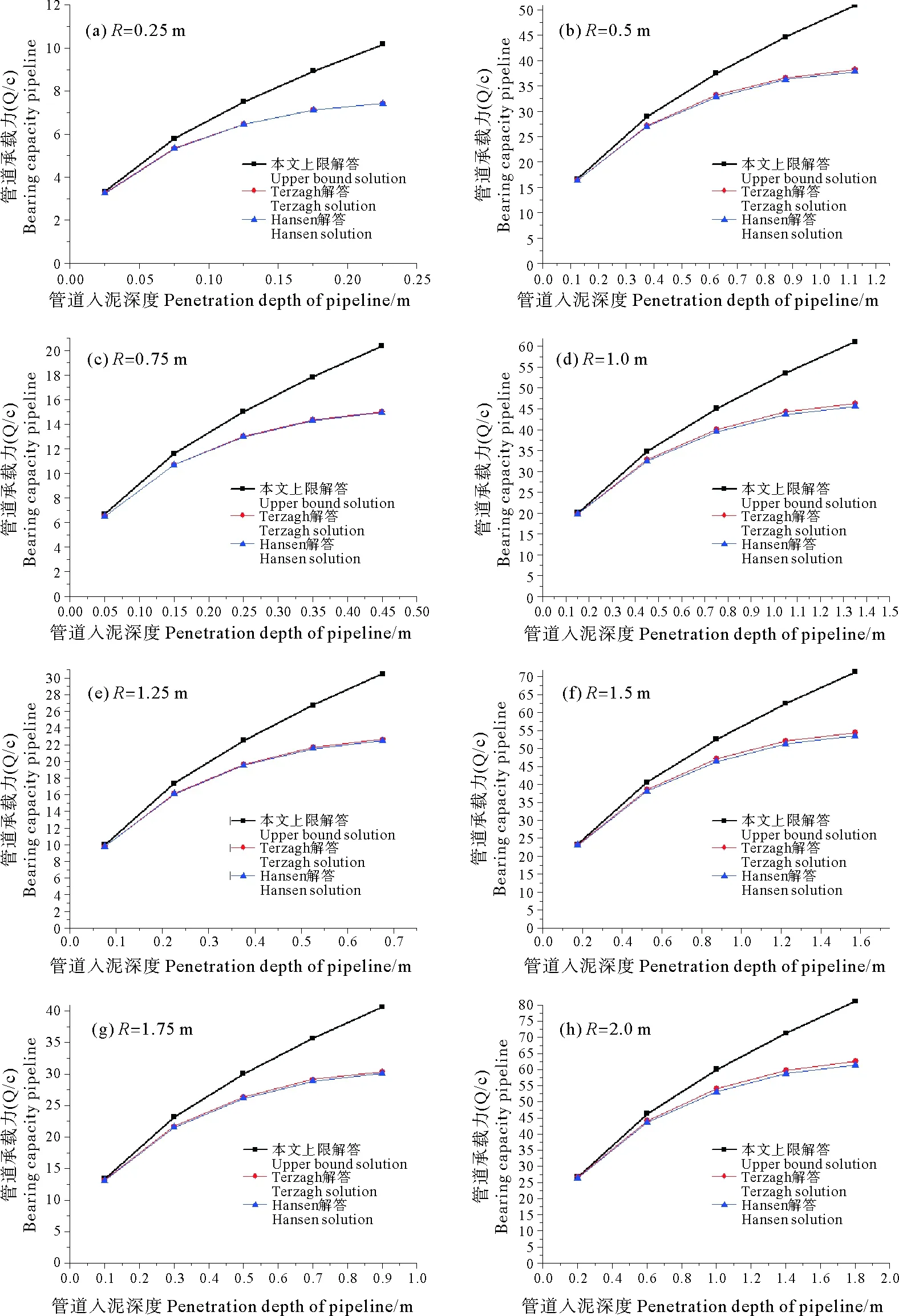
图5 本文上限解答与部分理论公式对比图(φ=20°)

为了进一步验正本文上限解答的合理性，将计算结果同Terzaghi、Hansen计算公式进行了对比，对比结果如图4、5和6所示。

图4结果表明，本文给出的圆形管道周围土体失效模式产生的内能耗散率较大，能够提供较大的极限承载能力。当土体内摩擦角较小时，与圆形管道接触的土体，随着圆形管道的逐渐贯入，土体发生挤压-剪切塑性变形，比Hill塑性剪切破坏模式下耗散的内能大；此时，Terzaghi计算公式中的Nγ较小，所以本文解答高于Terzaghi公式计算结果。

图5所示结果表明，随着海床土体内摩擦角度的增加，Terzaghi破坏模式中的被动破坏区逐渐扩大，被动区重力耗散的内能逐渐增大，Terzaghi公式计算结 果逐渐逼近本文上限解答；当土体内摩擦角进一步增大，如图6所示，地基承载力系数Nγ将进一步增加，Terzaghi和Hansen计算结果将明显增大。

图6 本文上限解答与部分理论公式对比图(φ=25°)

针对二维条形基础，图7中弹性核周围123区域表示摩擦角为15°时，管道周围土体内能耗散区域；弹性核周围456区域表示摩擦角为20°时，管道周围土体内能耗散区域；弹性核789区域表示摩擦角为25°时，管道周围土体内能耗散区域；可以发现，随着土体内摩擦角的线性增加，基底土体内能耗散率将呈现非线性增大，而且被动破坏区域重力耗散功率与土体总耗散功率的比值将逐渐扩大，从而导致Terzaghi地基极限承载力系数Nγ较大。

由于圆形管道与海床接触时，接触面为圆弧形状，导致管道周围土体变形规律较为复杂，变形过程中土体剪切能耗散较大，跟Prandtl假定的条形基础底部主动土压力刚性剪切破坏模式不一致，圆形管道周围土体不再发生主动破坏，而是在管壁曲面挤压下发生塑性挤压-剪切变形，类似于小孔扩张，从而比Prandtl破坏模式吸收更多的塑性剪切畸变能。此时，圆形管道贯入海床过程中，管道周围土体的挤压-剪切塑性变形耗散的内能高于Terzaghi对数螺旋区域耗散的内能，如图4所示。随着土体内摩擦角的逐渐增大，Terzaghi公式将给出较大的土体极限承载能力，而本文尚未考虑土体重度对圆形管道承载能力的影响，故呈现出本文上限解答与Terzaghi承载能力逐渐接近，如图5、图6所示。针对不排水饱和软黏土情况，由于土体内摩擦角为零，按照本文给出的破坏模式，将得到较为理想的极限承载能力与入泥深度，与闫澍旺教授提出的修正Prandtl计算公式较为接近[2]，如图8所示。

图7 不同摩擦角下土体内能耗散区域

图8 饱和软黏土海床上限解答(φ=0°)

本文推导结果表明，采用二维条形基础承载力Terzaghi计算公式，用管道与海床泥面相交的管道横截面作为基础宽度，计算的极限承载能力较小，所以工程上一般对圆形管道横截面位置进行假定，将横截面下移一定深度，视管道为浅埋基础，从而提高圆形管道的极限承载能力[2]。

3 结论

基于岩土塑性力学极限分析上限定理，借鉴Hill可动速度场模式，本文推导出了砂性海床上浅埋圆形管道的极限承载力与入泥深度上限解答。通过将Terzaghi理论解、Hansen理论解与本文上限解的对比，可以得出：

(1) 考虑管壁周围土体的剪切变形耗散能，能够提高管道的极限承载能力。文中给出的管道周围土体运动速度场满足运动许可条件，圆管周围土体在管壁挤压下发生塑性剪切变形，类似于小孔扩张，从而比Prandtl破坏模式吸收更多的塑性剪切畸变能。

(2) 本文上限解答给出的管道入泥深度与承载能力，能够为进一步深入研究管道与土体相互作用提供一定的理论支持。

[1] 海洋石油工程设计指南编委会. 海洋石油工程设计指南: 海洋石油工程海底管道设计[M]. 北京: 石油工业出版社, 2007.

Offshore engineering design guide. Guide for design of Offshore Oil Engineering：Offshore oil engineering design of submarine pipeline[M]. Beijing: Petroleum Industry Press, 2007.

[2] 施红伟, 闫澍旺. 海底管道的沉降量计算[J]. 中国海洋油气(工程), 2003, 15(2): 1-4.

Shi Hongwei, Yan Shuwang. Calculation of settlement of submarine pipeline[J]. China Offshore Oil and Gas(Engineering), 2003, 15(2): 1-4.

[3] Merifield R, White D J, Randolph M F. The ultimate undrained resistance of partially embedded pipelines[J]. Geotechnique, 2008, 58(6): 461-470.

[4] White D J, Randolph M F. Seabed characterisation and models for pipeline-soil interaction[J]. Int Journal of Offshore & Polar Engng, 2007, 17(3): 193-204.

[5] Krost K, Gourvenec S M, White D J. Consolidation around partially embedded seabed pipelines[J]. Geotechnique, 2011, 61(2): 167-173.

[6] 陈惠发. 极限分析与土体塑性[M]. 北京: 人民交通出版社, 1975.

Wai-Fah Chen. Limit Analysis and Soil Plasticity[M]. Beijing: China Communications Press, 1975.

[7] 王仁, 熊祝华, 黄文彬. 塑性力学基础[M]. 北京: 科学出版社, 1982.

Wang Ren, Xiong ZhuHua, Huang WenBin. Fundamentals of Plasticity Mechanics[M]. Beijing: Science Press, 1982.

[8] 栾茂田, 张其一 等. 均质地基上浅埋矩形基础极限承载力上限分析[J]. 海洋工程, 2008, 26(2): 69-77

LUAN Mao-tian, ZHANG Qi-yi et al. Upper bound limit analysis of bearing capacity of rectangular shallow footing on homogeneous clays[J]. The Ocean Engineering, 2008, 26(2): 69-77.

[9] 张国祥, 付江山. 基于极限分析的圆形浅基础地基承载力上限解[J]. 岩土力学，2010, 31(12): 3849-3854.

ZHANG Guo-xiang, FU Jiang-shan. Upper bound solution for bearing capacity of circular shallow foundation based on limit analysis[J]. Rock and Soil Mechanics, 2010, 31(12): 3849-3854.

[10] 张学言, 岩土塑性力学基础[M]. 天津: 天津大学出版社, 2004.

Zhang XueYan. Fundamentals of Geotechnics Plasticity[M]. Tian Jin: Tianjin University Press, 2004.