镜头畸变和照度随主光线角度变化的优化分析

叶果，刘智颖，徐百威，刘建华

（1.长春理工大学 光电工程学院，长春 130022；2.中国人民解放军驻五五九厂军事代表室，无锡 214035）

随着互联网的发展以及广大消费者对于手机拍照需求的日益增长，手机像素从最初的100万、200万、500万［1］，发展到了现在的800万甚至是千万像素。在CMOS没有出现以前500万像素、800万像素的手机镜头的光学总长度至少在10mm以上［2］随着手机感光元件加工工艺以及产品性能的提升，像元尺寸从先前的5μm迅速发展到现在的1.4μm甚至1.1μm［3］，通常镜头的长度是与成像质量成正比的，而在手机镜头上，因为长度要制造得非常小，就必须在其它参数上做补偿［4］，这对手机镜头的设计提出了更高的要求。为了充分使用高分辨率的图像传感元件的分辨能力，通常采用4片透镜元件如美国专利764655、7609454。除了影响MTF的各种像差，在大视场高像素手机镜头的设计中像面照度优化显得尤为重要。良好的照度优化能消除暗角，能进一步提高手机镜头在暗光环境下的成像质量。在对手机的像面照度进行优化时，一定的负畸变有利于改善光学系统的相面照度，但是过大的畸变将会引起轴外视场分辨力的退化并且失真严重影响使用效果［5-7］，在以往的手机镜头设计中均未对手机镜头的像面照度优化设计进行细致的讨论，本次设计结合仿真中的数据变化，使用MATLAB对优化得到的数据点进行拟合，为优化手机镜头的像面照度提供可靠依据。

1 理论分析

1.1 镜头的光学畸变

在系统畸变可以忽略的条件下，根据小孔成像的理想模型，可以将线性的成像系统描述成下式：

当物体到镜头的距离有限时：

当物体到镜头的距离无限远时：

镜片径向曲率的变化会使像点沿径向移动，导致图像便变形，离中心点越远，其变形量越大。正的径向变形量会使图像向远离图像中心的方向移动，其比例系数增大；负的径向变形量会引起点向靠近图像中心的方向移动，其比例系数减小。

1.2 光学系统的畸变率：

通过引入了畸变率来衡量图像的畸变程度。畸变率的定义如下

其中，η表示实际成像高度即实际成像点到图像中心的距离；H为理想成像高度即理想成像点与图像中心的距离；D表示畸变率。根据式（3）可知，当图像产生的是枕型畸变时，有η＞H，那么畸变率D应为正数；当图像产生的是桶形畸变时，则η＜H，畸变率D为负数。

1.3 光学系统的像面照度

光学系统轴上像点的经典照度公式［8］为

式中τ为光学系统透过率，n，n'为物空间和像空间折射率，u'为轴上视场成像光束的像方孔径角。当物像空间介质相同时n=n'为物空间和像空间折射率，u'为轴上视场成像光束的像方孔径角当物像空间介质相同时，n=n'，（4）式变为

利用几何光学进行推导，可以得到轴外视场角ω视场对应的像面照度按照规律下降：

联立（5）（6）可得：

由此公式可知像面照度受到主光线角度的影响。

2 手机镜头的优化

2.1 设计要求

镜头的F#为2.4，视场角大于60°，光学总长小于4.1mm。1/2极限频率处全视场的MTF值大于0.5，畸变小于2%。

2.2 初始光学结构

图1 使用的初始结构

非球面透镜的光学系统计算初始结构比较困难，故从专利中选取由4片塑料非球面镜片和1片滤光片组成的初始结构。分析专利的初始结构，第一块透镜是双凸面的，通过减小透镜的曲率可以改善光学系统的光学总长第二块透镜是双凹面的，将第二块透镜设计为在近轴区是凹面的在离轴区域是凸面的，这时候该表面上从离轴区域投射到图像传感器的光线的角度能够被有效的减小，能够提高光学系统的像面照度，而且能够校正轴外像差［9］。第三块透镜的前表面为凹面后表面为凸面，在整个系统中起矫正像散的作用。第四块透镜的前表面为凹面后表面为凸面，在整个光学系统中能够校正系统的高级像差和像散［10］。此外，合理的增大最后一片镜片的光焦度，能够有效地减小轴外光线在图像传感器上的投射角度，改善系统的成像质量。优化前的MTF曲线、场曲畸变、垂轴像差和相对照度、如图2，图3，图4和图5所示。

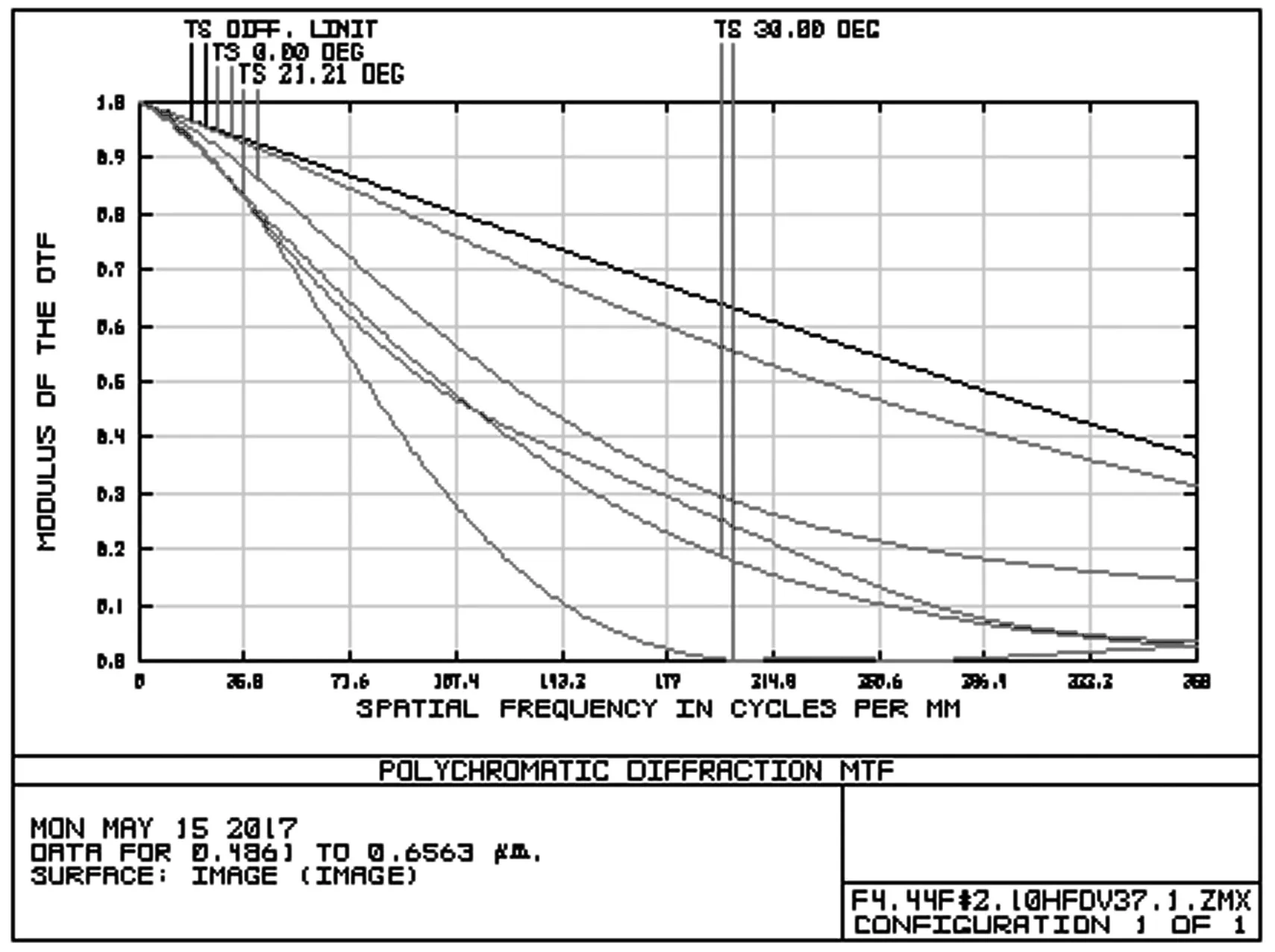
图2 优化前的MTF曲线

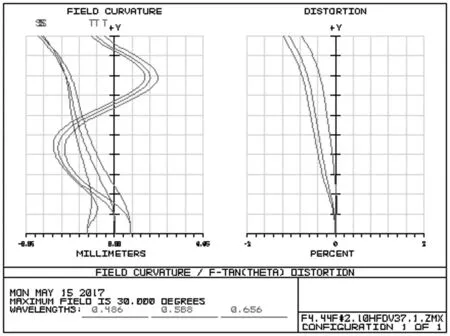
图3 优化前的场曲和畸变曲线

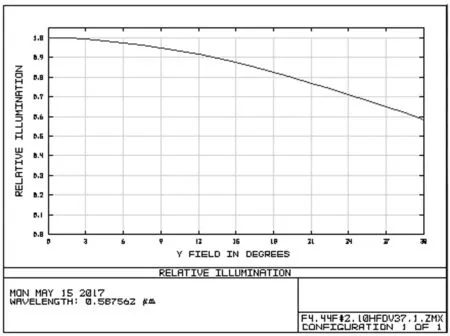
图4 优化前的相对照度曲线

图5 优化后的MTF曲线

通过操作数对各类像差进行限制，进行逐步优化。结构优化时发现由于较大的视场和短总长，本设计的场曲和畸变不容易控制，为了减小场曲将第三块透镜手动修改为厚透镜，并适当加厚第四块透镜校正场曲，同时过小的畸变值将会增大其他像差导致设计不符合要求，故在整个优化过程中始终用DIMX限制最大畸变值在1.9%处为其他像差的调整留出空间。除了畸变，为了在边缘处得到更好的照度值，使用RAID减小主光线的角度，并用MTFT提升边缘视场的像质，使照度满足要求。经过优化后如图6、图7所示。

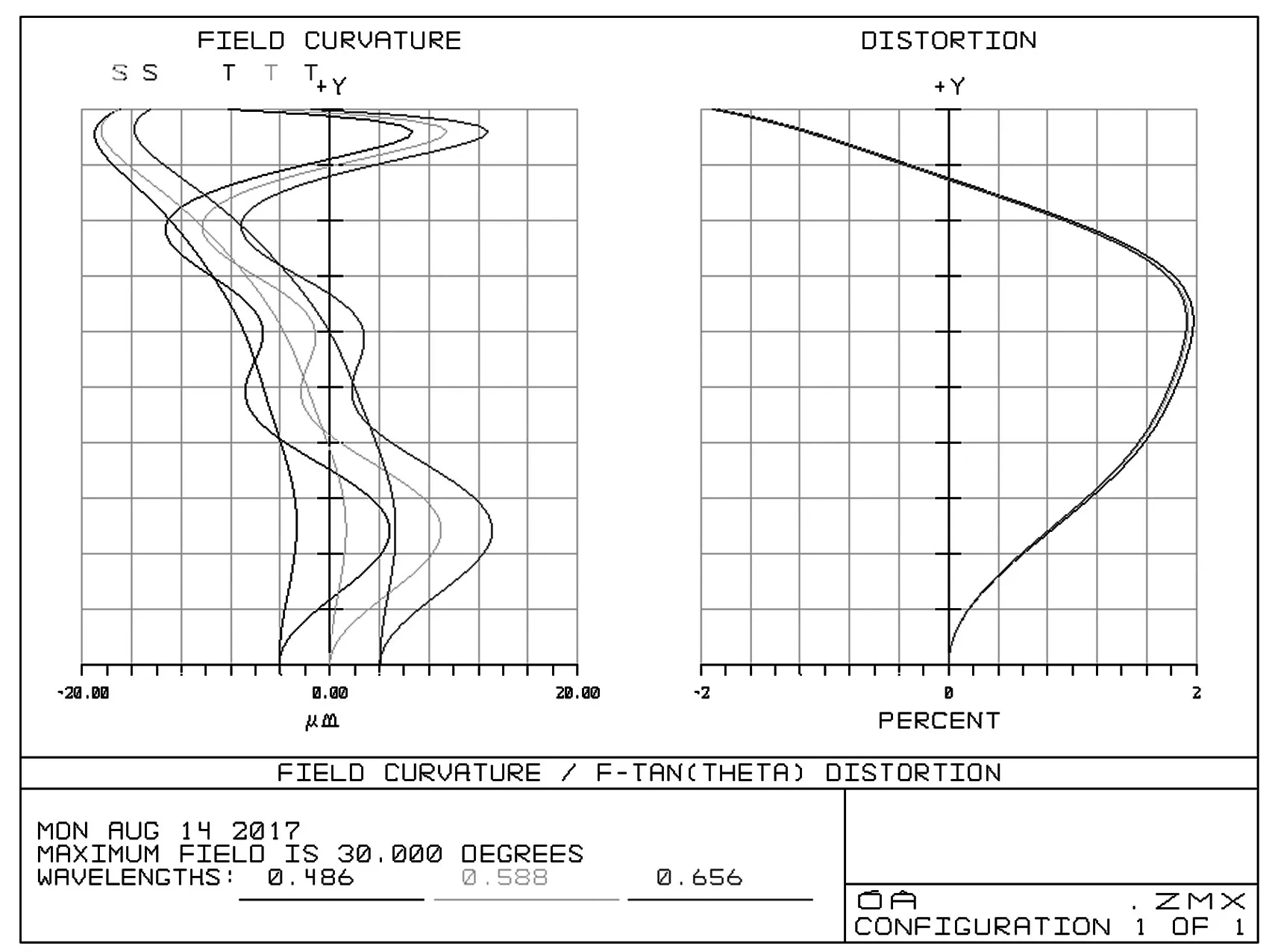
图6 优化后的场曲和畸变曲线

图7 优化后的相对照度曲线

3 主光线入射角度与畸变和相面照度的关系

3.1 仿真数据分析

在对照度进行优化的过程中，发现边缘照度与畸变主光线角度具有较强相关关系。于是，将已经优化完成的设计结构作为模拟的对象，鉴于设计要求为畸变小于-2%。因此本文决定以畸变值为-2%为起点，为防止变化过大对结构产生较大影响，降低数据可信度每次减小畸变值仅为0.1%，得到数据如表1所示。控制系统的场曲像散慧差球差，保证系统的最大畸变小于2%系统全视场MTF大于0.5，得到优化数据的散点图，如图8、图9、图10所示。

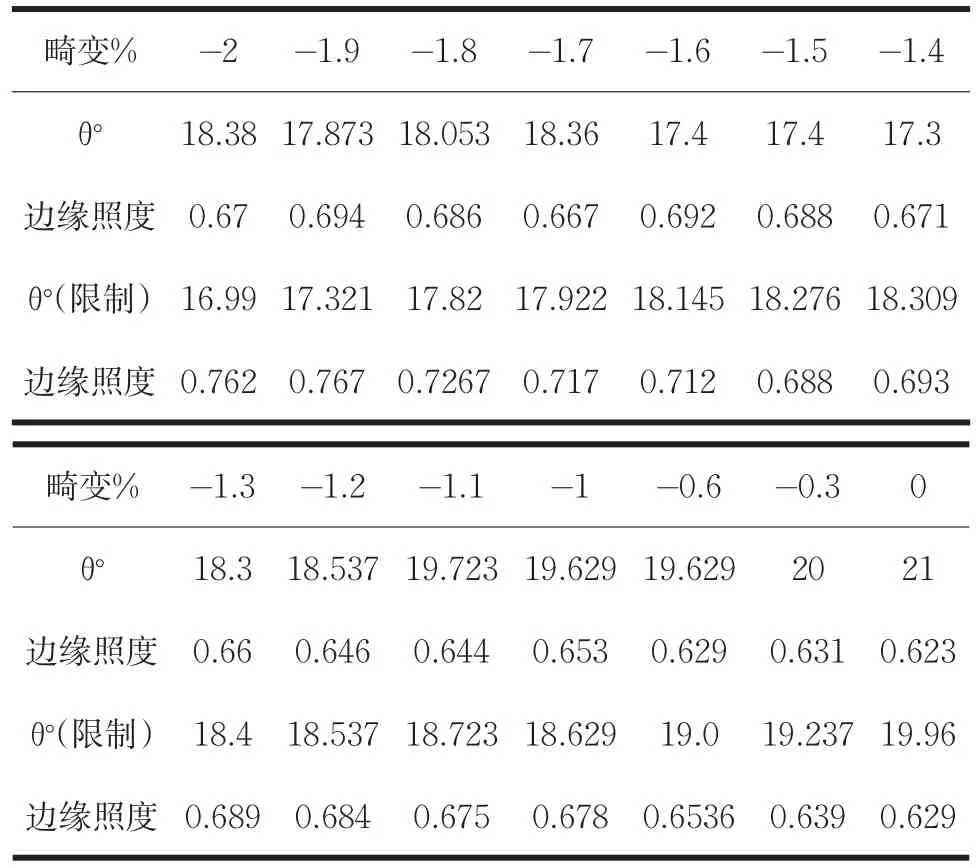
表1 未限制边缘主光线和限制边缘主光线对照

图8 畸变与主光线角度相关关系

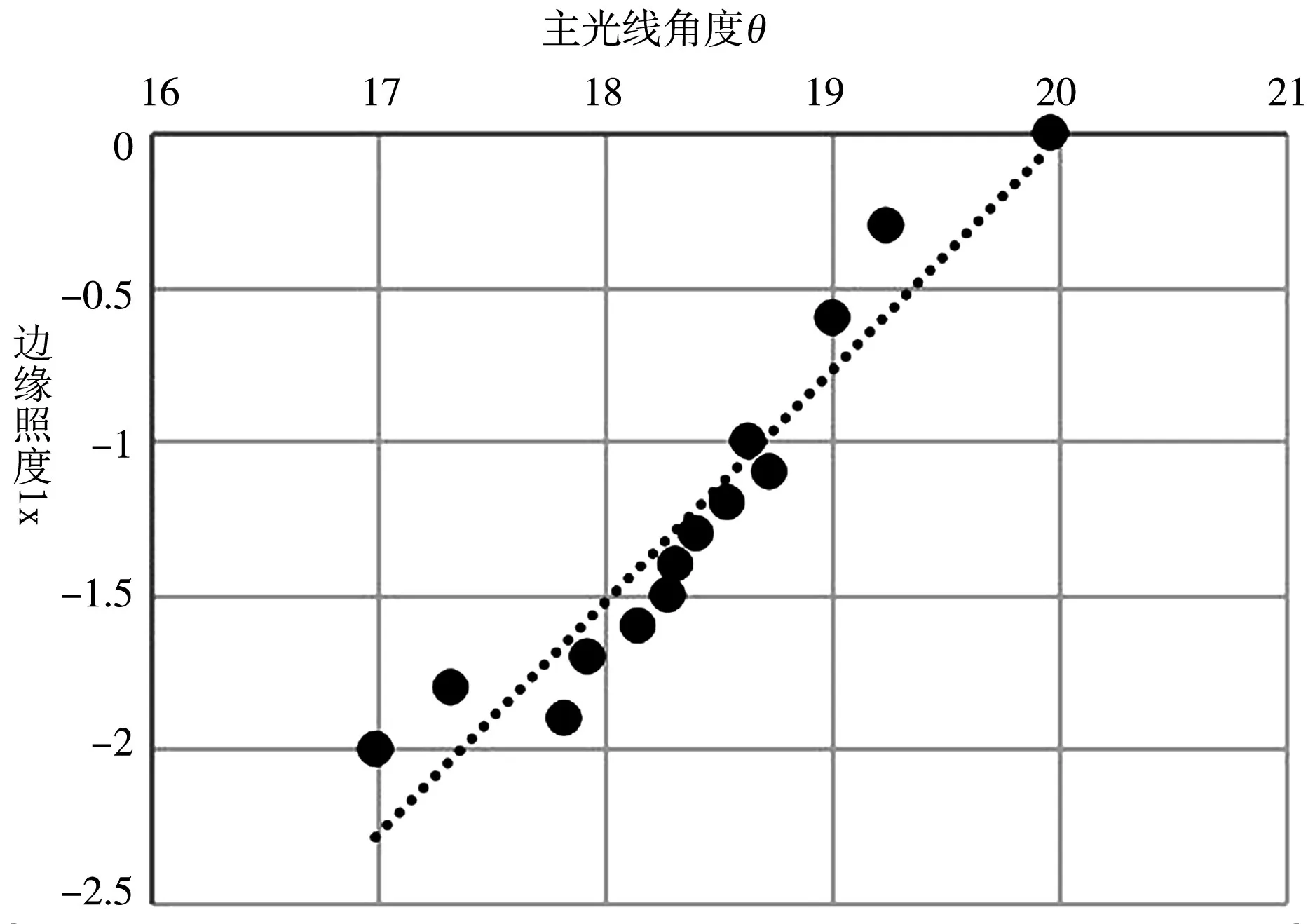
图9 边缘照度与主光线角度的相关关系

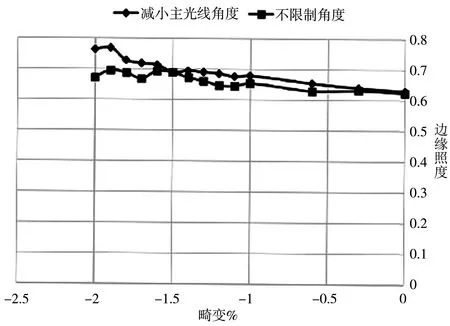
图10 控制主光线后照度对比图

图8说明畸变随主光线角度增大而减小。图9说明边缘光照度也随主光线角度增大而减小。对于设计要求需要在光照度和畸变要求达到平衡，求解出最佳主光线角度。图10不主动控制主光线出射角度在不同畸变条件下的优化结果和降低主光线入射角度的优化结果的对照。说明主动控制边缘主光线角度有利于改变边缘照度情况。通过对照数据发现边缘畸变最优点在-1.5%左右，主光线角度在0.95视场为17.5°。以17.5°为基础能找到系统的平衡解。记录了不同主光线角度条件下，边缘相对照度和边缘畸变的走势，在图11中标记出了满足最小照度条件下的畸变、照度和主光线角度，在图12中标记出了满足最小边缘畸变条件下的畸变、照度和主光线角度。

图11 满足要求的最小照度

图12 满足要求的最小边缘畸变

3.2 优化结果

普通优化方法结果如图13和图14左图所示，结合Matlab分析出最优主光线角度的优化结果如图13和图14右图所示。

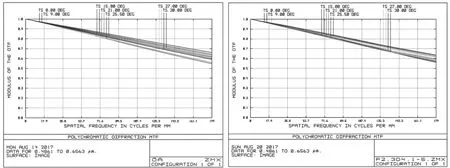
图13 优化结果与原始MTF曲线对比

图14 优化结果与原始照度曲线对比

4 结论

利用Zemax对大视场光学系统进行照度优化时，没有相应的优化操作数，只能通过调整系统的边缘光线来优化边缘照度，通过仿真数据显示在优化过程中一定的负畸变有利于改善像面照度，对主光线进行优化时，畸变和像面照度呈现线性变化，存在一个特定的主光线角度使得畸变和相对照度有最优解，通过对数据的统计得到系统满足条件下的最优边缘畸变值与边缘主光线大小，得到满足要求的设计结果。经仿真实验得出的结论，适用于大视场光学系统出现边缘照度低的情况，对于系统的优化设计具有指导意义。

［1］张萍，王诚，宋东璠，等.500万像素手机镜头设计［J］.应用光学，2009，30（6）：934-938

［2］李文静.500万像素手机镜头的光学设计［J］.激光与光电子学进展，2009，46（1）：56-59.

［3］杨周，阳慧明，丁桂林.一款超薄800万像素手机镜头的设计［J］.应用光学，2013，34（3）：413-419.

［4］丛海芳.4P超薄800万像素镜头设计［J］.红外与激光工程，2014，43（12）：3993-3997.

［5］于艇，迟名辰，李艳红，等.1300万像素折衍混合式手机镜头设计［J］.长春理工大学学报：自然科学版，2015，38（6）：5-11.

［6］李广，汪建业，张燕.800万像素手机镜头的设计［J］.应用光学，2011，32（3）：421-424.

［7］彭雪峰.基于CodeV的800万像素手机摄像镜头设计［J］现代科学仪器，2012，144（4）：71-74.

［8］屈恩世，张恒金，曹剑中，等.对光学设计中照度计算公式的讨论［J］.光学学报，2008，（7）：1364-1368.

［9］刘宵婵.变焦手机镜头的设计［D］.长春：长春理工大学，2009.

［10］尹志东.800万像素手机镜头的光学设计与制造［D］.长春：长春理工大学，2014.