期望与方差的应用

孙晓玲

(合肥师范学院 数学与统计学院，安徽 合肥 230601)

1 引言

《概率论与数理统计》是研究随机变量统计规律性的学科。该课程有严密的理论体系，其结论和方法有很强的应用性，在生产实践、经济管理和社会生活中有众多的应用案例。本课程的理论和方法与数学、物理学、计算机科学的诸多分支都有密切的联系，在培养大学生综合素养方面发挥着重要的作用[1-3]。

随着信息技术的发展，学习早已超越课堂，已经成为可以随时、随地发生的终生行为。为了适应人们能够利用碎片时间随时随地学习需求，“微课”应运而生了。“微课”是指在较短时间内，有明确的教学目标、内容短小，集中说明一个问题的小课程。微课的兴起与发展源于网络教育的迅猛发展，它的出现满足了人们个性化学习、按需选择学习的愿望，既可查缺补漏又能强化巩固知识，是课堂学习的重要补充和拓展[4-7]。

由于微课需要在10到15分钟以内完成传统课堂1到2节课的教学内容，这就要求微课制作者合理设计教学内容，在课程中引入新的教学方法、教学手段和教学理念。本文根据全国首届(2015)高校数学微课程教学设计竞赛中的微课教学案例“小李的选择”来阐述概率论与数理统计中期望和方差在经济决策中的应用步骤和方法。

2 应用实例

2.1 教学内容分析

要全面的掌握随机变量的统计规律性，必须了解这个随机变量的分布函数。但在实际问题中，要求得随机变量的分布函数往往很困难，也没有必要。通常只需要了解到随机变量的几个数量指标即可，这些数量指标就是随机变量的数字特征。期望和方差是概率分布中最重要、最常用的数字特征，它们在金融决策中发挥着重要的作用。这里将以微课教学案例“小李的选择”为例说明期望与方差在经济决策中的应用步骤和方法。

2.2 教学案例—“小李的选择”

问题背景小李有30万元想购买理财产品，若存银行，一年可获得利息收益9300元，为了保值增值，小李更倾向于购买具有较高收益的理财产品。对工作人员推荐的产品A，B，C，小李让业内朋友帮忙分析获得了三种理财产品的盈亏分析。业内朋友帮小李绘制了一年后三种产品获得收益的情况如下图1、图2、图3所示：

图1 理财产品A的预期收益

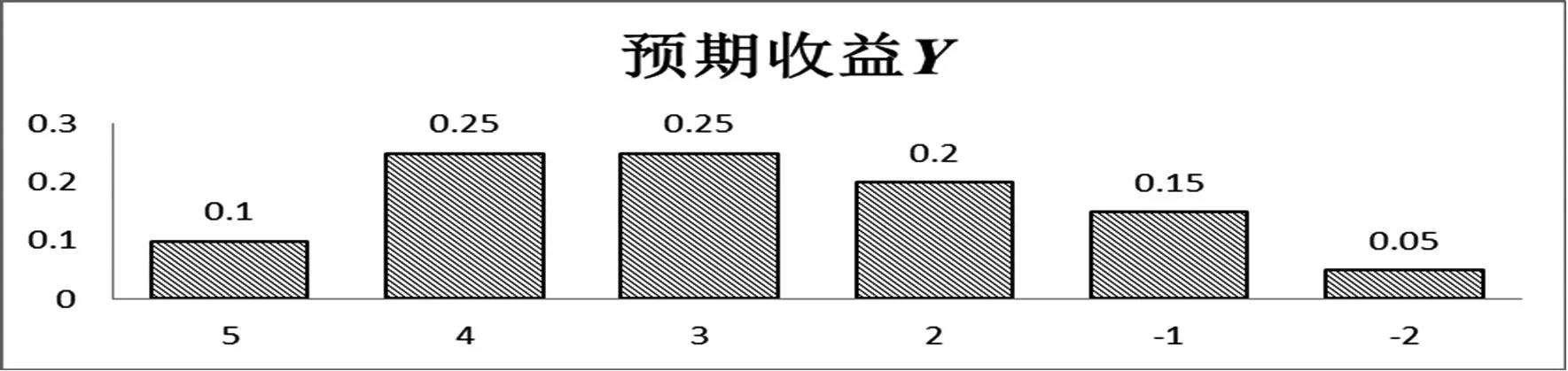
图2 理财产品B的预期收益

图3 理财产品C的预期收益

问题提出看到上图，小李感到很困惑，还是不知该如何选择，接下来就讨论能否利用期望和方差的知识帮助小李做出合理的选择。根据讨论的结果可以引出期望和方差的概念，也能让学生切实感受到期望和方差概念的应用。

问题分析在帮助小李做出选择之前需要明确理财产品的选择标准。小李之所以选择购买理财产品是因为其相对于其它理财方式所具有的高收益。因此，可将高收益作为购买理财产品的一个选择标准。但是鉴于理财市场经常流行一句话“高收益、高风险”，小李还想在保证一定收益的情况下尽量降低风险。因此，还需要考虑另外一个选择标准：低风险。

确定好了高收益，低风险这两个选择标准之后，小李又面临了另一个问题，由于理财产品的收益都具有不确定性，确定了选择标准后又该如何量化预期收益呢？下面就分别以高收益，低风险作为选择标准来量化各个理财产品的预期收益从而帮助小李做出选择。

2.2.1 问题解决：选择标准1：高收益

由于收益具有不确定性，因此可以用随机变量表示收益，将这三种产品一年后的收益分别记为随机变量X，Y，Z。显然，它们都是一维离散型随机变量。从上面的柱状分析图可以分别看出三种理财产品的预期收益X，Y，Z的概率分布分别如表1、2、3所示：

表1 预期收益X的概率分布

表2 预期收益Y的概率分布

表3 预期收益Z的概率分布

由于理财产品收益取值有多个，仅仅了解了预期收益的概率分布还是不能确切知道一年后各产品的具体收益，因此可以用数学期望来代表这个预期收益。数学期望是随机变量的数字特征之一，它表示随机变量取值的平均水平。离散相随机变量的数学期望定义如下所示：

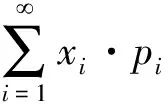
数学期望的本质以概率为权值对随机变量取值的加权平均，即随机变量取值的均值。

可以根据理财产品A，B，C预期收益的概率分布数据，再利用Excel软件中的SUMPRODUCT(A1:G1*A2:G2)函数计算出X,Y,Z的数学期望，如表4所示：

表4 预期收益的数学期望

利用Excel现场演示计算不仅能够省去传统课堂黑板书写演示的时间，还能让学生感受到数学软件对学习的强大辅助作用。从表中容易看出，若以期望收益最大为标准进行选择，小李应该选择平均收益最大的产品B。但是在这种风险投资中，高收益往往伴随着高风险，风险投资者们进行投资，必然要关注被投资项目的风险是不是在他可接受的范围之内。若风险超出了他能承受的范围，即使预期收益再高投资者也很可能不会冒大的风险进行投资。因此下面还需要考虑第二个选择标准：低风险，由此可引出方差的概念。

2.2.2 问题解决选择标准2：低风险

如何评估风险？

在某一特定环境下，在某一特定时间内，经济学中度量收益不确定性的指标，可用方差进行度量。方差是用来度量随机变量和其数学期望(即均值)之间的偏离程度，定义如下：

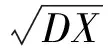
方差的本质方差是用来度量随机变量取值与其数学期望之间的平均偏离程度的量，方差越小，则随机变量与其数学期望的偏离程度越小，随机变量的取值就越集中在期望值附近。

方差的概念与生活密切关联。在风险决策、经济决策、证券投资、效益评估、产品质量评估等领域都有广泛的应用。

要利用方差帮小李按照第二个选择标准：低风险进行选择，可根据三种理财产品的预期收益X，Y，Z的概率分布表以及相应数学期望值数据，再应用Excel软件中的SUMPRODUCT(((A1:G1)-H1)^2*A2:G2)函数计算得到下面的表5：

表5 预期收益的方差

从表5可以看出若以低风险作为理财产品的选择标准，显然要选择产品C，而若以高收益为选择标准的话显然要选产品B，那么到底该如何抉择呢？为了让投资更加稳妥，下面将两个选择标准综合考虑进行决策。

3 综合决策

为了选择收益最高、风险最低的产品，不妨以产品C的收益和风险为量纲来评估风险。

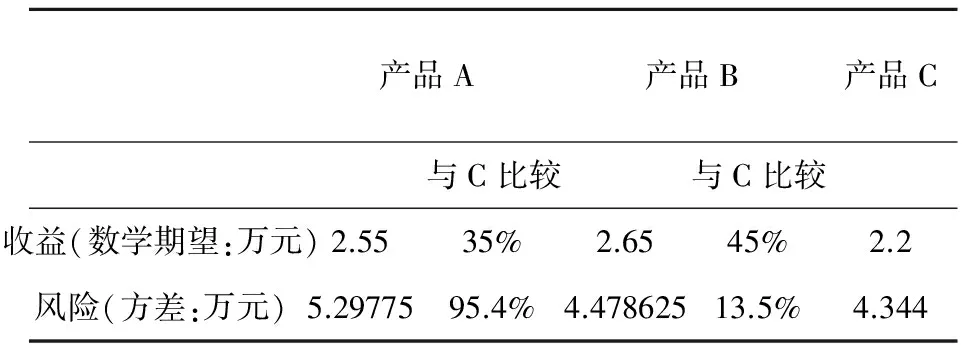
表6 风险评估表

从表6可以看出，与产品C相比，产品A收益增加35%，风险增加更多，达到95.4%。而产品B与C相比，收益增加45%，风险却只增加13.5%，收益增幅高于风险增幅，综合考虑，可以建议小李选择产品B。

若选择的对象更多，数据量更大，可以将上面的选择过程进一步量化。可将上表中的收益增幅与风险增幅相除，得到一个评判数据，则表6可以变为以下表7形式：

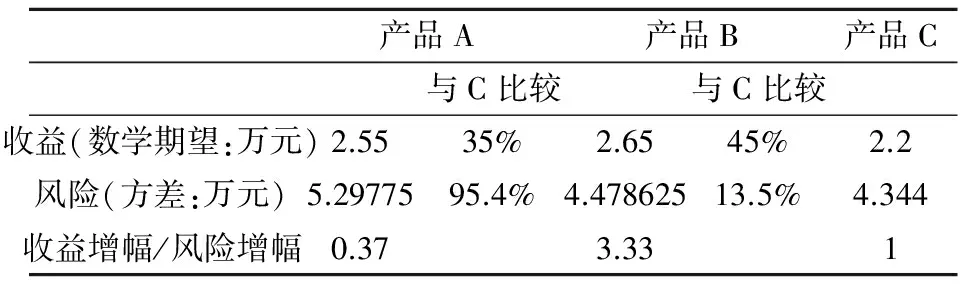
表7 综合评估表

从比值来看，产品B具有明显优势，因此建议小李选择产品B。

小结利用期望和方差进行综合决策，可以首先根据数学期望估算出一个相对平均的收益值，为决策提供一个具体的数据依据，虽不是完全准确，但可以为决策提供一个具体的方向。方差可以反映数据的波动水平，有利于帮助人们得出相对准确的判断和正确的抉择。

综合来看，应用数学期望和方差进行综合决策的步骤有以下几步：

步骤1引入随机变量，表达不确定性问题；

步骤2应用数学期望，获得预期目标；

步骤3应用方差，评估获得预期目标的风险；

步骤4综合考虑，合理决策。

4 结束语

由于在平时个人消费、求职、投资、企业营销方案等日常生活和经济活动中，经常需要对各种遇到的情况和可能做出决策，以便以最合理有利的方式采取行动。由于决策经常受到随机因素的影响，因此决策常带有一定的风险。为了尽可能的规避风险，人们常将数学期望和方差作为综合决策参考的重要依据。文中给出的微课案例不仅能够让学生学习到期望和方差的概念，还能让学生了解到期望和方差在经济决策方面的应用。当决策问题较为复杂，数据量较大时，基于期望和方差的综合决策方法可以为决策者提供较有力的参考工具，并获得较大的经济效益及社会效益。

[1] 马奕, 涂淑珍, 吕卫平. 微课在概率统计教学中的应用与思考[J]. 广西民族师范学院学报, 2016, 33 (3):53-55.

[2] 严兰兰, 刘胜兰. 借助翻转课堂来提高大学数学教学质量[J]. 东华理工大学学报(社会科学版), 2016, 1:89-92.

[3] 崔静, 申广君. 大学数学微课教学可行性探究——以概率论与数理统计为例[J]. 大学教育, 2016,6:169-170.

[4] 曲文蕊. 初探大学数学微课建设——以级数定义的应用为例[J]. 学周刊, 2015,30:9.

[5] 胡铁生, 周晓清. 高校微课建设的现状分析与发展对策研究[J]. 现代教育技术, 2014, 24(2): 5-13.

[6] 张一川, 钱扬义. 国内外“微课”资源建设与应用进展[J]. 远程教育杂志, 2013,6:26-33.

[7] 钟绍春, 张琢, 唐烨伟. 微课设计和应用的关键问题思考[J].中国电化教育, 2014,12:85-88.