初中统计与概率教学中若干问题的探讨
张 磊
(芜湖市三汊河初级中学,安徽 芜湖 241000)
教育部2001年7月颁布了全日制义务教育《数学课程标准》(实验稿),2003年3月印发了《义务阶段数学课程标准》,2011年12月颁发全日制义务教育《数学课程标准》(修正版),加大了中小学统计概率的教学改革的力度,增加了许多统计概率和数据处理的内容.现在初中数学课程由代数、几何、统计与概率、综合实践应用等四大模块构成, 将统计概率放到与代数、几何同等重要地位.而随着统计概率逐步进入初中数学课程,必然带来许多教学上的问题.
1 统计与概率教学中存在的若干问题分析
1.1 教师的专业知识薄弱
要给学生一瓢水,那么老师得有一桶水.如果教师自身缺少专业知识,那么很难想象学生怎么会学得好.统计和概率不同于一般的确定性数学,统计中不仅注重平均数、中位数、众数等的分析运用,更重要的是统计意识的培养,概率中许多概念是抽象难以理解的,比如随机性和确定性、概率与频率、对立和相容等.从这个角度讲,如果教师专业知识不足,不能深刻理解知识脉络,教学抓不住重点,也找不出有效的方法,那么教学必然会进入误区,学生学习起来当然更吃力.
教师专业知识不足,探究原因有两点:已有的知识不足、继续教育不足.一些历史原因,教师尤其是农村地区的教师在统计和概率方面的专业知识掌握的不够扎实,不能够进行知识的延伸和拓展,而在原有的统计和概率知识水平不高的情况下,教师面临新课程等一些问题的出现,没有重视继续教育,没有及时的补足知识储备,使得在统计与概率方面教学存在诸多误区和问题.
误区之一:做一个抛硬币的实验验证等可能性
分析抛硬币确实是一个有助于学生感受随机性的简便易行的实验,但将其引进课堂却会适得其反,因为等可能性是思想上的,在实际的实验中由于各种因素,我们并不能得到预期的结果,这恰是随机现象的随机性和可能性的体现.在100次抛硬币的实验中想出现50次正面的概率是
这显然是个小概率事件,同我们的理解“抛一枚硬币,出现正面的概率为0.5,那么抛100次应该有50次正面”相差甚远,实验结束后,学生反而更糊涂了.
建议教师可以将学生分为若干小组,各个小组进行抛硬币的实验,然后把实验数据汇总.最后让学生看一下许多数学家抛硬币实验的结果,最后总结出现正面朝上和反面朝上的概率是相同的.面对出现正面和反面向上次数不同时,教师要从概率和频率出发科学的解释这种现象,概率是指某随机事件发生可能性大小的数值度量,它是随机事件本身的属性,是一个客观存在常数,而频率是指某随机事件在随机试验中实际出现的次数与随机进行试验次数的比值,是随机的,在不同的次实验中是不一定相同的.频率是概率的近似值,两者存在偏差,而且偏差是经常的,这就是随机现象的特性。
误区之二:把统计方法得出的结论绝对化
师:学校要开运动会,我们班要派一个人去参加跳绳比赛,这是小红和小玲跳绳的成绩

选手第一次第二次第三次第四次小红100110126130小玲98122100146
从这个表同学们得到了什么信息?
生1:小红的成绩很稳定,每次都能跳100多个.
生2:跳的最多的是第四次小玲跳的,146个.
生3:跳的最低的也是小红,她成绩忽上忽下.
师:那这次学校的比赛,我们应该选谁去呢?为什么呢?
生:小红,因为尽管跳的最好的那次是小玲跳的,但是她成绩不稳定,而小红成绩不仅很稳定,而且还是逐步上升的.
师:你分析的很对......
分析数理统计是“归纳”科学,是由“部分推断整体”,而不是“演绎”科学.因此,统计规律未必蕴含因果关系.这里小红的成绩一直呈上升趋势,这仅仅只是一个归纳性的结论,是我们由数据归纳出来的,并不是必然的结论,不是说她参加比赛就一定会跳的更好,一定会超过小玲的最高成绩.
建议教师在教学过程应引导学生体会统计思维,注意到统计结果的随机性,统计结果有可能是犯错误的.统计规律未必蕴含因果关系,这是统计方法的本性.统计学对于结果的判断标准是“好”、“坏”,教师在教学中应该把握这个判断原则,防止给出“对”、“错”的判断.不同的情境,应该给出不同的选择.比如,如果参加的是射击比赛,需要计算每一轮射击成绩的总和,那么可能选择成绩呈上升状态的选手;如果参加的是跳绳比赛,需要选择最好的成绩作为结果,那么可能选择那位跳出最好成绩的选手.
1.2 没有把统计和概率作为整体进行教学
这与教材的内容设计有很大关系,除了几个让学生统计掷硬币正反面朝上的次数,使学生感受不确定现象外,“统计”教学与“概率”教学内容都是分开的,而且因为教师专业知识的不足,所以,教师很少能注意到在统计教学中渗透概率知识的教学.实际上统计与概率是联系紧密的,概率是研究大量偶然事件中规律性的科学,统计是以概率论为基础的,对统计资料进行分析研究并导出其概率规律性的科学,即通过统计资料研究从一定总体中抽出的样本的某些数学特征所表现的概率规律性科学[6].比如,抽样统计是以随机事件为基础的,又比如,大数定律中频率趋近于概率.所以,统计和概率联系紧密,将两者结合起来教学,更有助于学生把握整体,从而更好体会统计概率在实际生活中的应用.
1.3 教师的教学经验不足
众所周知,统计和概率进入中学课本时间不长,虽然以前的教材有存在一些统计和概率的知识,但名存实亡.在新的课程标准下,统计和概率的教学对于教师而言是一片空白,不少教师在教授统计和概率知识时,虽然知道它的不同于代数、几何知识,但是该如何进行有效教学,还是没有摸索出办法,加之前人对此研究甚少,只能摸着石头过河.如此教学,必然会出现问题.
例如:师:同学们,老师这里有一个袋子,袋子里面有5个球,有4个红色的,1个白色的.同学们猜猜,如果老师从里面摸一个球出来,会是什么颜色?
生(齐):红色的.
师:很好,那同学们猜猜我摸红色球的概率是多少?
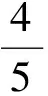
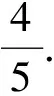
……
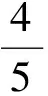
建议告诉学生袋子里有很多球,有白色的,有红色的,让他们分小组实验摸球,记录每次摸出球的颜色,让学生自己去发现摸出红球的次数比白球多,由此推断可能红球的个数多于白球.实验次数足够多的话,在收集大家的数据后,有可能估计出红球和白球的个数比例.再告诉袋子里球的个数,那么就差不多知道白球多少个,红球多少个了.有经验的老师会用适当的方式让学生成为学习的主导者,让学生经历探索的过程,由所学知识来逐步解决面对的未知,逐步形成随机观念和统计思想,渐渐在实际生活中运用这些知识,获得本领.
1.4 教学中过于强调计算
不单单是统计和概率,在整个数学的教学中普遍存在这个问题.到底该如何去教?现在一些统计课变成统计图的简单绘制,概率课变成排列组合的计算,学生学会了统计却不知道统计到底有什么用,学会了概率而不懂得如何运用概率来指导生活中的一些决定.主要原因还是教师在专业知识方面和教学经验上面的欠缺,老师自身并没有清楚教学的目的,没有在教学中渗透统计和概率的精髓,强调计算偏离了统计和概率的真正意义.
例如:平均数、中位数、众数的教学
分析在平均数教学上,教师往往习惯于引导学生列式计算,总结出数量关系:平均数等于总数除以总份数.然后就通过大量习题来巩固这个数量关系,忽视了概念的理解和统计的理解.统计教学的重要目标是鼓励学生从数据中提取有效信息,体会数据中蕴涵着的信息,因此,应该注重对数据整理、描述、分析方法的理解,而不只是单纯的计算.
建议理解平均数有三个角度:算法理解、概念理解、统计理解.教师应该引导学生再观察分析数据,发现在例题中的公司里大多数人的工资水平低于平均数,得出结论,在一些案例中平均数并不能很好的反映总体.在平均数教学过程中,教师应该多举例帮助学生体会平均数的意义,而不是仅仅练习总结出来的数量关系公式.教师应该告诉学生平均数、众数、中位数都可以表示一组数据的平均水平,虽然平均数在生活中比较常用,但是容易受到极端数据的影响.众数不受极端数据的影响,但可靠性比较差.中位数计算简单,且不受极端数据的影响,但不能充分利用所有数据的信息.在具体的情况下,应考虑用哪种数据表示平均情况更为合理。
1.5 信息技术水平低
进行多媒体教学,是教学的薄弱环节,探究其原因,有:学校的基础设施和教学设备比较欠缺和落后;由于统计和概率学科的特点,对于课件制作水平要求比较高,而教师不具备这样的课件制作水平;一块黑板一只粉笔的传统教学方式影响着教师,还没有形成用多媒体教学的习惯.然而《课程标准(2011年版)》指出:“把现代信息技术作为学生学习数学和解决问题的有力工具,有效地改进教与学的方式,使学生乐意并有可能投入到现实的、探索性的数学活动中去”.利用多媒体进行概率论中的随机事件的模拟、统计学中的各种统计图的展示对于学生自主学习有极大裨益.多媒体展示的课件图文并茂、丰富多彩,不仅有利于学生通过观察、实验、探究、猜想、验证、推理与交流,而且也为教师节约了不少课堂时间.但是教师需要注意在多媒体教学中课件的播放速度要适宜学生进行记录,多媒体只是教师上课的辅助工具,切不可让眼花缭乱的课件完全吸引学生的注意而忽视上课内容.
在统计概率的教学中,大量随机事件的发生,大量的数据处理,计算机和计算器就能帮上很大的忙.在人教版的数学教材中很好的渗透了信息技术的使用,附有计算器计算的一些使用方法,这样学生能够利用计算器的使用,减少计算的时间,体会到信息技术与人类生活的息息相关.在计算过程中应渗透这些计算工具的使用,使得学生学会充分利用工具,更好统计规律性.
1.6 教材内容的不足
1.6.1 教材内容与城市生活联系密切,农村教师教学有困难
统计和概率与实际生活联系紧密,比如家庭每月用水量,NBA球员身高,沙尘暴天气次数变化等,教材的编者没有注意到这些研究调查的对象对于农村孩子来说是比较陌生的,教师在教学时需要改造调查的对象,使得学生易于采集信息、数据整理,进行分析,而这又增大了农村教师的教学难度,但若不花大力气进行改造,学生学起来体会不到统计和概率与他们自身生活的联系,更谈不上培养用统计和概率解决实际问题的意识了.教材的活动和调查内容应该更加大众化,一点一滴将统计概率的思想和方法渗透到生活中.
1.6.2 培养学生动手能力方面欠缺
有研究表明:在与美国的统计和概率课程的比较中,很容易发现西方国家对于学生的实际动手能力有很高的要求,而我国学生动手能力较差,包括学生对于数据的收集,一些数学实验的开展.
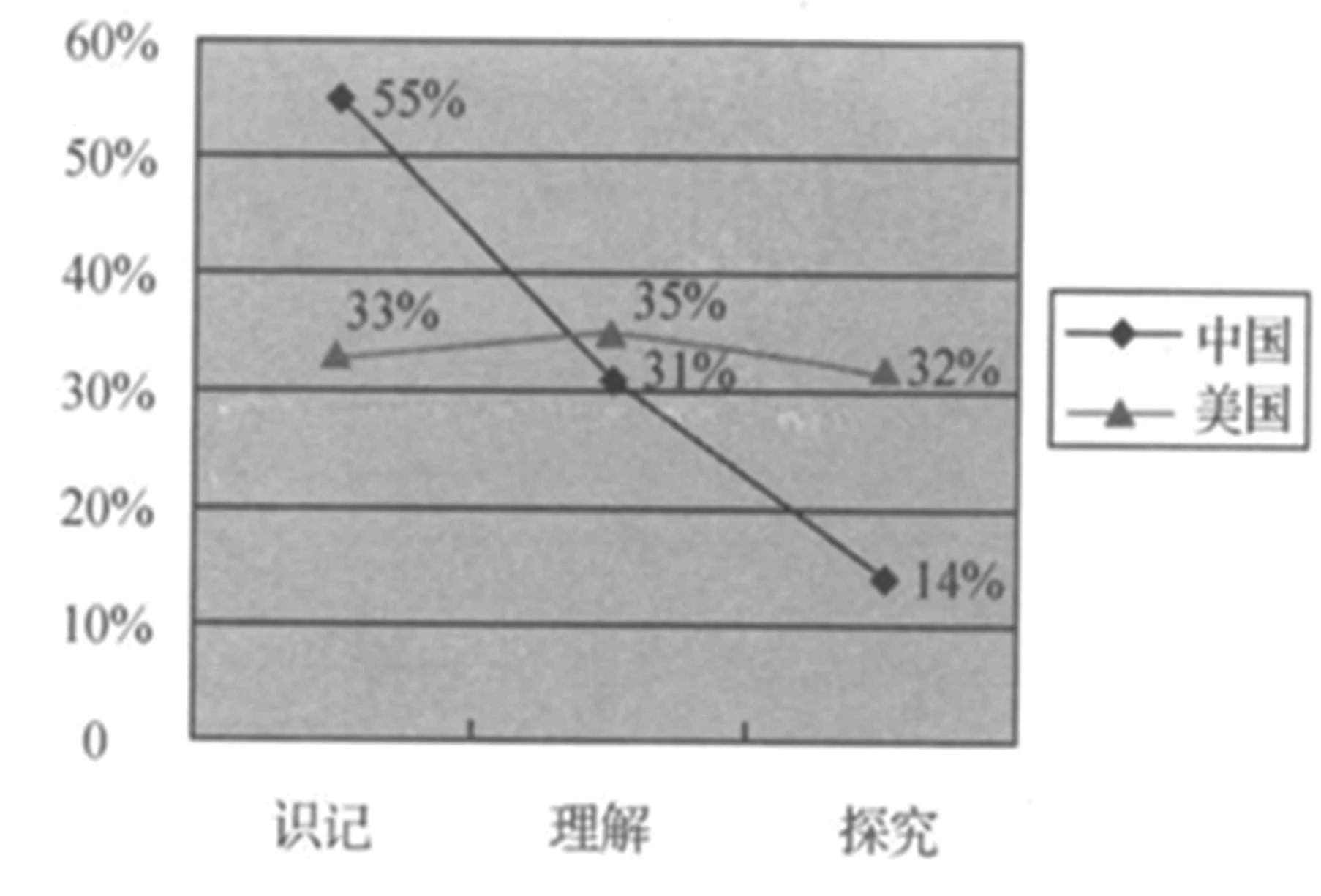
图1 中美初中数学统计和概率习题在探究上的水平折线图
从图中可以看出,美国的数学教材在统计和概率上要求识记的同时,注重理解和探究,而我国在统计和概率的内容上有失偏颇,比较注重识记,而不注意理解,忽视探究部分.其中识记水平的特点是机械性,缺少联系;理解水平的特点是常规性和封闭性;探究水平的特点是非常规性,开放性和探究性.习题是例题、练习题、习题及复习题等的总称.
纸上得来终觉浅,尤其是偏于调查探究的统计和概率学科上,动手探究是不可或缺的.纸上谈兵学不会统计和概率.
2 统计和概率教学的几点建议
2.1 注重继续教育,提高教师的专业知识
教师是知识的传播者,应该注重知识的延伸和拓展.俗语说:活到老,学到老.教师的专业知识是教学的基础,只有在不断的学习中,才能解决出现的新的教学问题,迎刃有余的教学.
2.2 注重统计和概率思想的渗透,加强对学生统计概率观念的培养
概率教学的重点是使学生掌握概率的基本思想和方法,强化应用性,培养学生应用数学知识解决实际问题的意识和能力.
2.3 合理运用现代信息技术,鼓励学生使用计算器等现代信息手段
现代信息技术在数学教学中的运用已经成为社会发展的要求了.电子表格对数据处理的功能非常强大;随机思想是统计概率的灵魂,随机模拟对随机概率事件的模拟非常有效,网络使数据收集变得很便捷.计算器、计算机的运用使得学生更加有效的学习统计和概率成为可能.
2.4 加强学生动手实践,培养学生探究能力
统计和概率在实际生活中有着广泛的应用.只有让学生参与进来,动手收集数据、整理数据、分析数据,才能够更深刻地体会到统计与概率的魅力.
[1] 中华人民共和国教育部制订.全日制义务教育教学课程标准(实验稿)[M].北京:北京师范大学出版社,2001.
[2] 中华人民共和国教育部制订.全日制义务教育教学课程标准(实验稿)[M].北京:北京师范大学出版社,2003.
[3] 黄岳俊.高师《中学统计概率教学与研究》课程体系建构[J].钦州学院学报,2008,(3):62-63.
[4] 裘红明,王培,周颖娴.美英澳三国初中统计概率课程对我国的启示[J].中学数学杂志,2008,(6):1-3.

