车辆-轨道系统时-空随机分析模型
徐 磊, 翟婉明
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
车辆-轨道耦合系统在时间、空间尺度下具有动力参数和激振源的不确定性,为了更细致、准确地反映该时变系统的动力学行为,需要将用于铁路线路“设计与建造”的确定性计算方法与非确定性的随机分析理论相融合。车辆-轨道(桥梁)耦合系统的动力随机分析,亦逐渐为国内外科研工作者所关注,文献[1]将轨道结构的扣件刚度和道床刚度作为随机参数,应用Monte Carlo(MC)随机有限元法,对中高速铁路设计动轮载和动力系数进行了研究;文献[2]运用车-桥垂向耦合模型,考虑车辆荷载及一、二系竖向弹簧刚度与阻尼的随机性,对车桥垂向耦合随机振动进行了计算分析;文献[3]将道床横向刚度的随机性与轨道原始弯曲、行车速度等因素综合考虑,进行无缝线路动力稳定性的概率计算;此外,Ricciardi[4]假设荷载幅值和到达桥梁时间的随机性,采用扩展的Ito微分法则求解梁的随机响应;Saeed等[5]对钢轨型面数据进行统计分析,将可靠度理论引入列车脱轨分析。
通过对既有研究的总结可知,目前关于车线(桥)系统随机性的研究取得了不少成果,但考虑系统时-空随机动力效应的车辆-轨道系统时-空随机振动模型尚未完整建立,主要原因有:
(1)车辆、轨道系统动力参数随时间维度的演化特性未知。
(2)轨道结构参数在空间维度的分布及演变规律未知。
(3)激振源概率信息不全。目前国内外绝大多数研究均通过对单一谱线进行反演所得到的时域不平顺样本作为激励,然而单一谱线仅代表铁路系统长期运营中某一概率水平下的激振幅值,不具有遍历性。
(4)计算效率的限制性。车辆-轨道系统随机变量的高维分布导致了计算量的剧增。
(5)激励输入与响应输出的概率传递机理不明,非确定系统宜采用概率方法进行描述。虽然可以进行大量确定性分析以逼近真实的系统随机行为,但直接导致计算量的增加,与(4)相悖,故需要进行概率密度演化与传递的研究。
对于具有空时演化特性的车辆-轨道耦合随机动力系统,其分析与控制是一项系统工程,从动力激扰因素的统计、模拟、组合,随机动力系统的建模,到系统输入-输出的随机概率特征传递与分析,各环相扣,而每一环均可作独立的子模型深入研究(见图1),此系统模型的建立必须借鉴多学科的研究成果。除轨道不平顺外,其他基础检测资料还不完善,本文主要假设系统参数的随机分布特性,重点对随机模型中涉及的参数模拟,随机变量联合概率计算、组合与降维,随机动力系统建模,系统响应的概率统计分析等内容做具体研究。

图1 车辆-轨道随机动力系统分析流程
1 车辆-轨道耦合动力模型
本文基于车辆-轨道耦合动力学理论[6],建立了车辆-轨道有限元耦合动力模型,包括车辆子系统、轨道子系统及轮轨界面系统三部分,见图2。
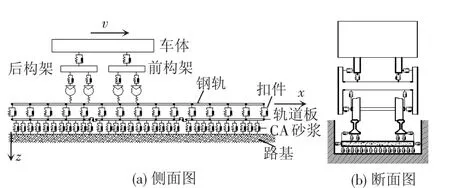
图2 车辆-轨道耦合动力学模型
车辆子系统为35个自由度的多刚体系统[1],主要考虑了车体、构架以及轮对的横移、沉浮、侧滚、摇头及点头运动,并通过一系、二系悬挂系统进行连接。轨道子系统则采用高速铁路中广泛采用的板式无砟轨道,采用有限元方法对其进行模拟。其中钢轨考虑为连续点支承的Euler梁,钢轨垫层模拟为线性刚弹簧及阻尼器单元,轨道板通过CA砂浆与路基连接,CA砂浆模拟为线性均布面弹簧和黏滞阻尼器,每个轨段单元40个自由度,见文献[7]。
另外,本文采用新型轮轨空间耦合模型[8]模拟轮轨界面的非线性接触几何关系,轮轨法向力用赫兹非线性弹性接触理论计算,轮轨切向蠕滑力用Kalker线性蠕滑理论和饱和非线性修正计算[9]。
本模型各子系统的动力学方程及不同子系统间的相互作用关系可参见文献[7],由于篇幅所限,此处不再赘述。
2 车辆、轨道及不平顺激振源的随机模拟
考虑系统内参数的随机性,车辆-轨道随机动力方程为
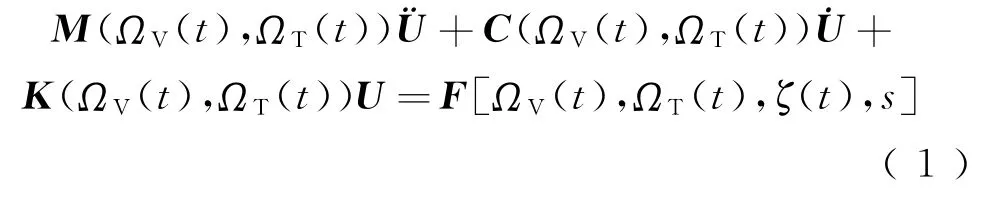
式中:M、C、K分别为系统质量、阻尼、刚度矩阵;U、˙U、¨U 分别为位移、速度及加速度响应向量;F(s)为轮轨相互作用力过程;ζ(t)为激励源随机域(如轨道随机不平顺);ΩV(t)、ΩT(t)分别为车辆系统、轨道系统的参数随机域,具有时变性。
对于上述建立的车辆-轨道耦合动力模型,其系统参数[ΩV(t),ΩT(t),ζ(t)]是确定的,不具概率意义和时变性。而车辆-轨道时-空随机振动模型是在车辆-轨道耦合动力模型的基础上考虑系统参数及激振源的随机性及长时效演化性,通过概率理论及随机模拟方法,将确定性计算与随机分析相结合而构造的动力模型。这里将分别给出车辆系统、轨道系统、轮/轨界面系统随机性的模拟方法。
2.1 轨道系统参数的随机模拟
轨道结构参数具有沿空间的随机性及随时间的变异性,但其变化规律尚不确定。文献[10]假定轨道结构参数沿空间独立随机分布,采用Karhunen-Loève(K-L)展开法建立轨道结构的随机场模型。本文给出一种考虑轨道结构参数相关性的随机模拟方法。
轨道系统为层式结构,考虑其物理力学参数沿x轴的空间变异性及相关性。其中,同一结构层的系统部件参数是非独立的,其相关系数为
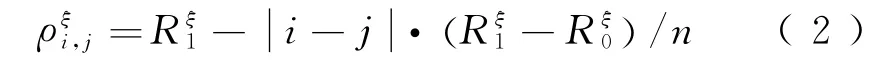
式中:i,j为部件单元编号值;ξ表示不同的系统部件(如扣件单元、CA砂浆等效弹簧单元等),ξ=1,2,…,k,k为部件数目;为相关系数的取值范围;n为总的部件单元数目。值越大,表示参数的空间相关性越强。通过式(2),可以形成n维相关正态分布随机变量抽样序列的相关系数矩阵
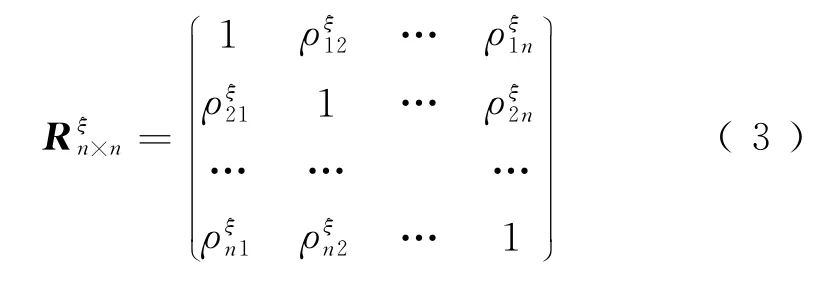
对于不同的系统部件 Uξ,令为需要产生的n维相关正态分布随机变量抽样序列,每个变量Xi(i=1,2,…,m)为m个服从指定概率分布的随机抽样列向量。对于Xξm×n的模拟,可采用如下步骤[11]:
Step1与同矩阵维数,生成独立标准正态分布随机变量抽样序列
Step2计算的协方差矩阵由于的对称与正定性[12],可对进行 Cholesky分解,即,其中为上三角矩阵;
Step3通过线性变换,令
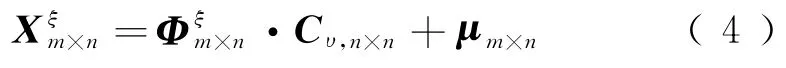
式中:μm×n为均值矩阵。
如此,便产生了具有指定相关性的正态分布随机变量抽样序列。同时,通过正态分布反函数迭代算法[13],可得的概率密度矩阵Prξ(i,j)(i=1,2,…,m;j=1,2,…,n)。
由于轨道参数沿线路纵向随机变化,故本文采用随机有限元法建立轨道结构的动力模型,并采用了一种循环计算的策略[14],实现了大长度连续建模和动力计算。
2.2 车辆系统参数的随机模拟
对于车辆系统,可以不考虑系统参数的空间变异性及相关性,仅考虑其动力参数随时间的变化,即对于某次确定性的车辆-轨道耦合动力学计算,其参数是恒定的;而对于不同时间点下的动力计算,其参数的样本向量变化。
对于不同的系统部件 Uζ,令为某单一部件ζ的n维正态分布随机变量抽样向量,总m个部件的抽样序列可构成抽样矩阵,则每个部件动力参数抽样序列对应的概率密度为根据不同的随机变量选点方法,对Ym×n进行重排序,可获得新的用于动力计算输入的样本矩阵即在动力学计算时,直接从的n个列向量中抽取m个动力学参数值进行车辆系统动力矩阵建模。
2.3 轨道不平顺的随机模拟
轨道不平顺是弱平稳的随机过程,以随机不平顺作为车辆-轨道系统的激振源,实际是其空间随机下的系统响应分析,而其随时间的演化规律尚不确定,但它在时域内的谱密度分布范围及概率分布是可以确定的。文献[15]根据轨道不平顺功率谱线的概率分布特性,给出了一种轨道不平顺的全概率随机模拟方法,极大地提高了计算效率,可将其应用于本文的研究。
3 车辆-轨道系统随机响应分析
3.1 随机变量集合
上述简单给出了车辆-轨道系统随机参数ΩV(t)、ΩT(t)及随机不平顺激振源ζ(t)的模拟及概率计算方法,记随机变量的集合为
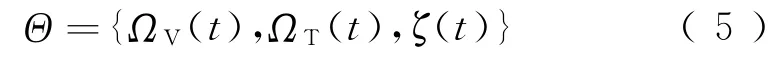
假定随机因素为相互独立的随机过程,采用MC法进行随机变量的集合选取时,存在效率低、随机收敛等问题。根据概率理论,随机变量的累计分布函数服从均匀分布,可以采用数论法[16]构造积分域内单位超立方体均匀散布点集,实现随机变量值的优选,令

式中:k=1,2,…,s,表示随机变量,且k∈Θ;j=1,2,…,n,n和hj构成整数矢量(n,h1,h2,…,hs),可加以筛选进一步降低选点数目,具体方法见文献[16-17]。
基于式(6)构造的点列xk,j均为单位超立方体[0,1]s内的散布点列,即xk,j∈[0,1],这正是累积分布函数的幅值分布范围,而随机变量的累积分布函数、概率密度分布及变量值一一对应。因此,可由点列xk,j确定车辆-轨道系统随机参数及激励源的具体取值。
3.2 概率密度演化
由于车辆-轨道系统参数和激励源的随机性,系统响应X(t)=(UT,˙UT)T也将是随机过程,其随机性来源于Θ。增广向量(X(t),Θ)的演化是一个概率守恒且保守的随机过程,Θ的输入概率与X(t)的响应概率间的概率传递可以用一类广义概率密度演化方程控制[18-19]。令(X(t),Θ)的联合概率密度函数pXΘ(x,θ,t),可得[19-20]
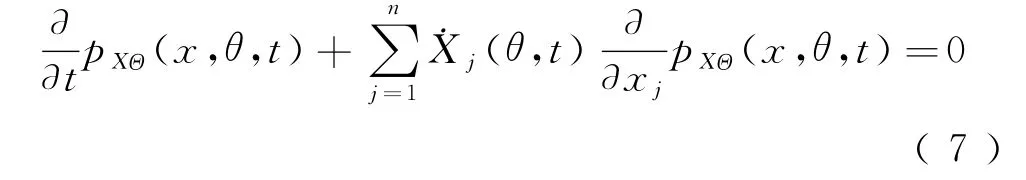
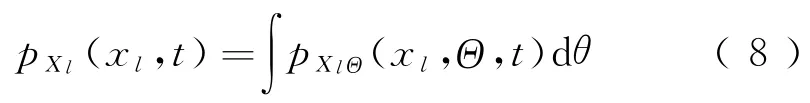
式中:pXl(xl,t)反映系统随机响应的幅值及统计概率信息,为系统随机响应、可靠度分析及低动力控制奠定了基础。需要注意的是,这里的时间t实际代表的是不同系统响应量在“缩聚”空间尺度的演化过程,亦即响应量经概率积分后在空间上的概率流动情况。
4 算例分析
基于前面的算法,给出一个数值算例,计算车辆系统和轨道系统在不同随机条件下的动力学行为。分析中采用CRH2型车,双块式板式轨道结构,行车速度为300 km/h。以武广高速铁路2013年全年的轨道不平顺动检检数据为系统随机激励源;由于系统参数随时间的变化规律善不明确,仅用变异系数表达,计算中系统随机参数以初始设计值为均值,假定服从高斯分布,取五挡变异系数0.05、0.10、0.15、0.20、0.25及未变异工况进行随机振动计算。
4.1 车辆振动响应
车辆-轨道系统在变异系数为0.2时,里程区段580~880 m内的车体垂向振动加速度概率密度演化曲面见图3。此概率密度演化曲面由车体振动加速度在不同截面的概率密度分布组合而成,反映了车体垂向振动响应在不同线路区段的概率分布。若概率分布较为集中,表明此区段之参数时变性对车体的垂向随机振动影响较小;反之,若概率分布较广,则此区段的车轨随机耦合参数对车体垂向振动不利,应重点加以分析。
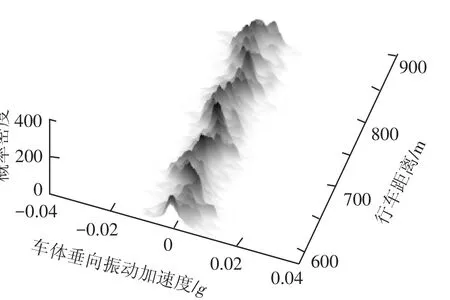
图3 变异系数为0.2时车体垂向振动加速度在某区段的概率密度演化曲面
将概率密度演化曲面沿行车距离轴向积分和归一化,可得时-空参数随机时系统响应的整体概率分布。轮轨垂向力、左轮轨横向力的整体概率密度分布见图4。由图4可知,无论是轮轨横向力还是轮轨垂向力,其振动响应范围及概率密度分布散度基本随变异系数的增加而增加。相对而言,系统参数的随机性对轮轨垂向力影响很大。德国联邦铁路(DB)规定[6],对于线路负荷,非冲击性的中低频轮轨垂向力不允许超过极限值170 k N。此极限值在系统变异系数为0.25时可能发生,见图4(a);同时,变异系数为0.05~0.20时,轮轨垂向力响应范围及概率分布均差别不大,但变异系数一旦达到0.25,则轮轨垂向相互作用将产生突变。
车辆系统不同动力响应指标的计算最大值及失效概率见表1。需要指出的是,表1中的失效概率是相对的。依据正态分布的基本特征,其横轴区间(μ-1.96σ,μ+1.96σ)内的面积为95.4%。本文取系统参数未变异、仅考虑轨道随机不平顺激励时动力响应累积概率在2.6%及97.4%时对应的响应值xl、xu为可靠度的吸收壁,即正常使用的要求为xi∈[xl,xu]。
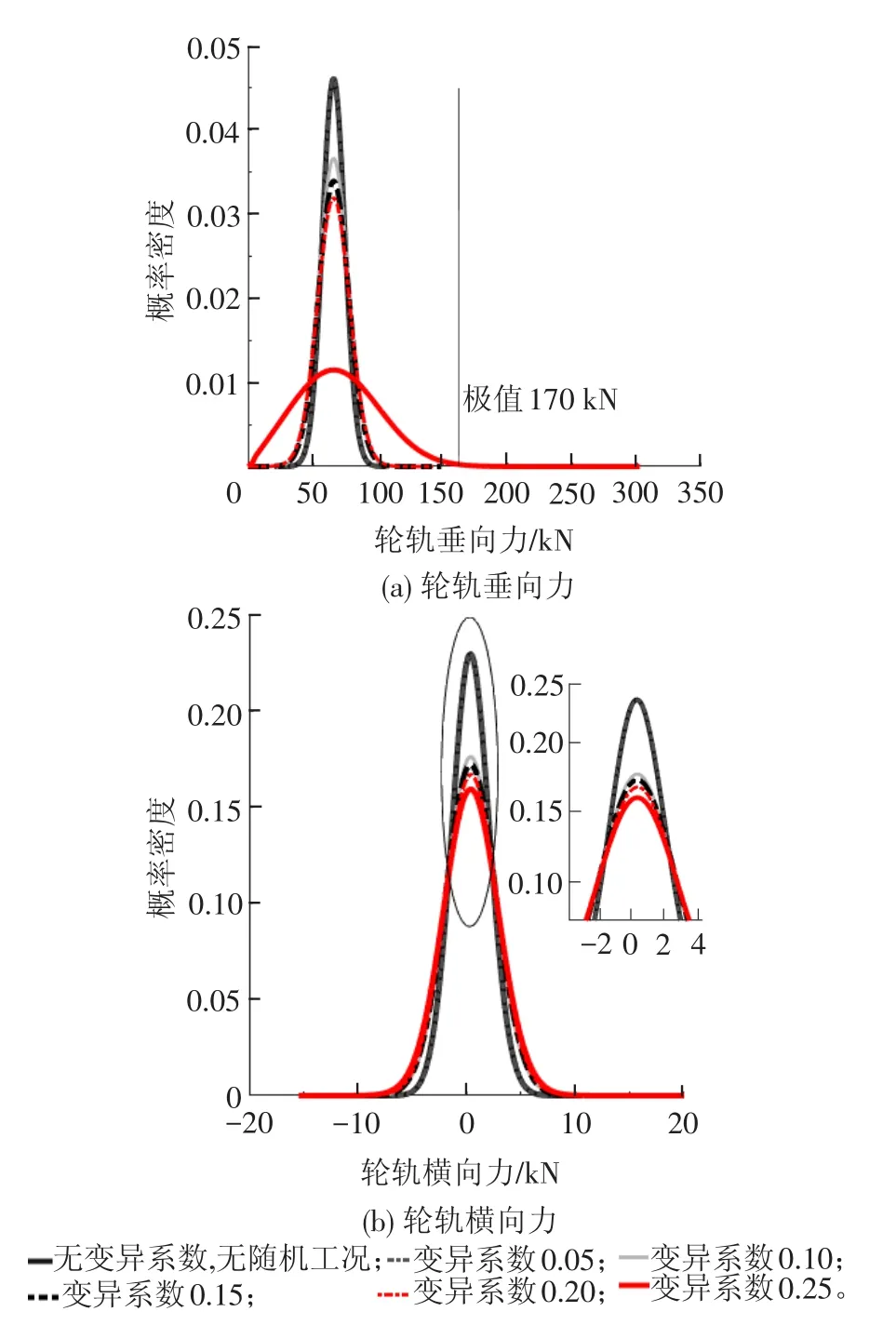
图4 在不同变异系数下的概率密度分布
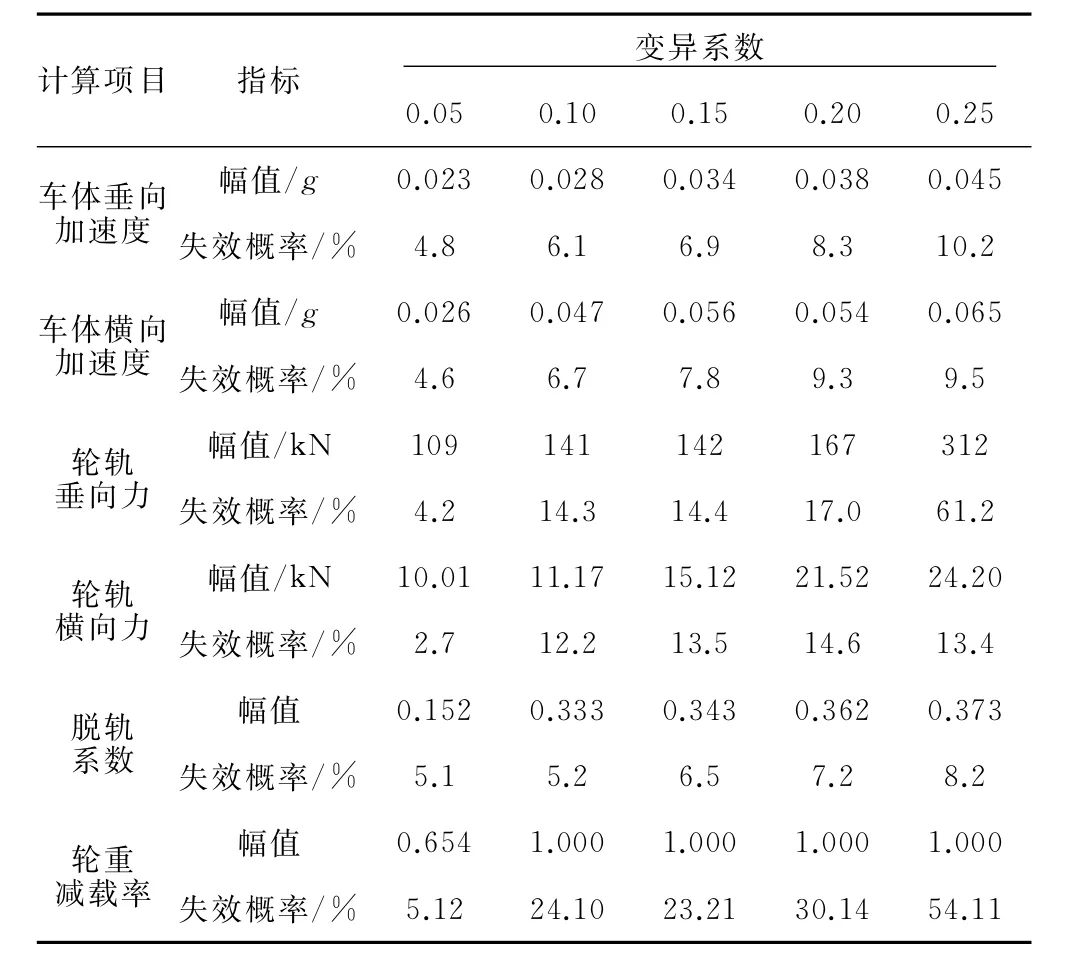
表1 车辆系统不同动力响应指标的计算最大值及失效概率
由表1可知,车辆系统不同动力指标随系统参数变异程度的增加(与时间相关),其计算响应范围及其失效概率基本递增。采用时-空随机振动计算方法,不同指标响应的概率分布pX,Θ(xi,θJ)可以计算出来,只需给定指标限值xi,可直接计算、使用可靠度,获得失效概率。失效概率反映了系统的时变随机状态,若能确定失效概率的限值,即可根据失效概率的时变曲线确定系统维修时间。
4.2 轨道振动响应
车辆系统不同动力响应指标的计算最大值及失效概率见表2。由该结果可知,系统参数的随机性对轨道结构的动力影响十分显著,随变异系数的增加,概率密度分布的离散性基本增加。钢轨在系统参数随机情况下的失效概率变化率要大于轨道板;同时,轨道系统的加速度响应对系统参数的随机性十分敏感,而位移响应相对较为迟钝,但也受系统参数随机的影响。
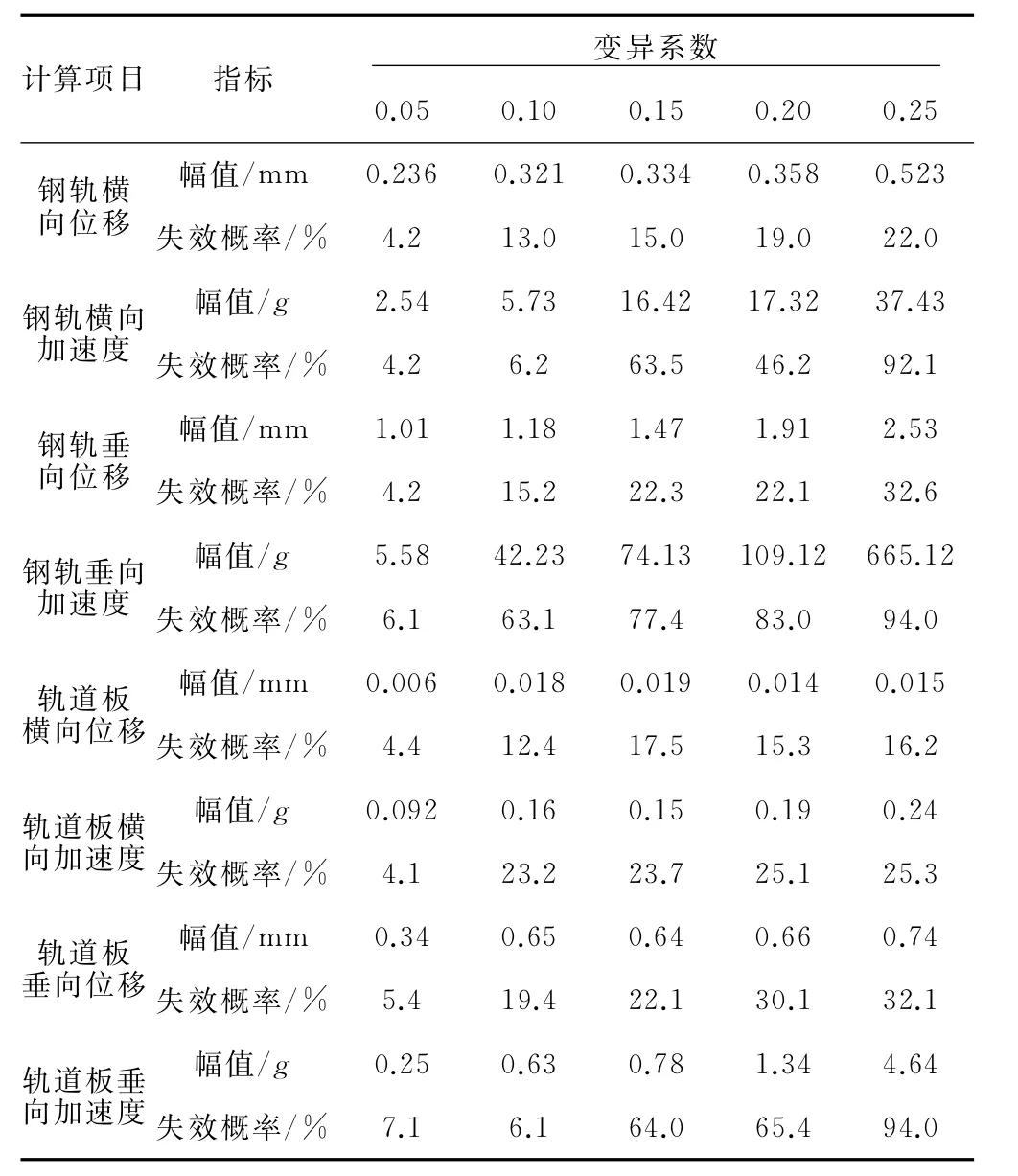
表2 轨道系统不同动力响应指标的计算最大值及失效概率
5 结论
(1)为进一步贴近车辆-轨道耦合系统在空-时域的随机性本质,本文给出了较为完整的车辆-轨道系统时-空随机分析模型。利用此模型,可以更好地研究车辆-轨道系统在耦合振动状态下的随机演化过程及其机理;此外,在系统长时效动力预测、演化机制及模糊动力限值制定等方面均可做深入的拓展研究。
(2)轨道随机不平顺数据较为完备,而对于车辆、轨道系统参数的随机特性,则没有完整的实测资料,因此应先假设其概率分布,再做具体的分析。由本文算例分析可知,依据本文模型获得的计算结果符合物理概念。
(3)研究表明,车辆系统和轨道系统均对系统参数的随机性较为敏感,体现了进行车辆-轨道系统随机分析的必要性。
[1]李斌,刘学毅.基于随机振动理论的我国中高速铁路有砟轨道设计轮载研究[J].铁道学报,2010,32(5):114-118.
LI Bin,LIU Xueyi.Study on Designed Dynamic Wheel Loads of Middle-speed and High-speed Railways in China Based on Theory of Random Vibration[J].Journal of the China Railway Society,2010,32(5):114-118.
[2]余志武,毛建锋,谈遂,等.车辆参数随机的车桥竖向随机振动分析[J].铁道学报,2015,37(1):97-104.
YU Zhiwu,MAO Jianfeng,TAN Sui,et al.The Stochastic Analysis of the Track-bridge Vertical Coupled Vibration with Random Train Parameters[J].Journal of the China Railway Society,2015,37(1):97-104.
[3]李秋义.高速铁路无缝线路动力稳定性概率分析理论研究[D].长沙:中南大学,2003.
[4]RICCIARDI G.Random Vibration of Beam under Moving Loads[J].Journal of Engineering Mechanics,1994,120(11):2361-2380.
[5]SAEED M,SOODABEH G.Estimation of Train Derailment Probability Using Rail Profile Alterations[J].Structure and Infrastructure Engineering,2012,8(11):1034-1053.
[6]翟婉明.车辆-轨道耦合动力学[M].4版.北京:科学出版社,2015.
[7]XU L,ZHAI W.A Novel Model for Determining the Amplitude-wavelength Limits of Track Irregularities Accompanied by a Reliability Assessment in Railway Vehicletrack Dynamics[J].Mechanical Systems and Signal Processing,2017,86:260-277.
[8]CHEN G,ZHAI W M.A New Wheel/Rail Spatially Dynamic Coupling Model and Its Verification[J].Vehicle System Dynamics,2004,41(4):301-322.
[9]SHEN Z Y,HEDRICK J K,ELKINS J A.A Comparison of Alternative Creep Force Models for Rail Vehicle Dynamic Analysis[C]//Proceedings of 8th IAVSD Symposium.Cambridge:Taylor&Francis,1983:591-605.
[10]徐磊,翟婉明.轨道结构随机场模型与车辆-轨道耦合随机动力分析[J].应用数学与力学,2017,38(1):67-74.
XU Lei,ZHAI Wanming.The Random Field Model for Track Structures and Vehicle-track Coupled Stochastic Dynamic Analysis[J].Applied Mathematics and Mechanics,2017,38(1):67-74.
[11]文德智,卓仁鸿,丁大杰,等.蒙特卡罗模拟中相关变量随机数序列的产生方法[J].物理学报,2012,61(22):1-8.
WEN Dezhi,ZHUO Renhong,DING Dajie,et al.Generation of Correlated Pseudorandom Variables in Monte Carlo Simulation[J].Acta Physica Sinica,2012,61(22):1-8.
[12]王梓坤.概率论基础及其应用[M].3版.北京:北京师范大学出版社,2007.
[13]郑铎,吴世伟.正态分布函数计算的建议及其反函数的非迭代算法[J].河海大学学报,1993,21(2):61-64.
ZHENG Duo,WU Shiwei.A Proposal for Computing Normal Distribution Function and a Non-iterative Method of Its Inverse Function[J].Journal of Hohai University,1993,21(2):61-64.
[14]XU L,CHEN Z,ZHAI W.An Advanced Vehicle-slab Track Interaction Model Considering Rail Random Irregularities[J].Journal of Vibration and Control,2017:1-12.(DOI:10.1177/1077546317731005)
[15]XU L,ZHAI W,GAO J.A Probabilistic Model for Track Random Irregularities in Vehicle/track Coupled Dynamics[J].Applied Mathematical Modelling,2017,51:145-158.
[16]LI J,CHEN J B.The Dimension-reduction Strategy via Mapping for Probability Density Evolution Analysis of Nonlinear Stochastic Systems[J].Probabilistic Engineering Mechanics,2006,21(4):442-453.
[17]华罗庚,王元.数论在近似分析中的应用[M].北京:科学出版社,1978.
[18]李杰,陈建兵.随机结构非线性动力响应的概率密度演化分析[J].力学学报,2003,35(6):716-722.
LI Jie,CHEN Jianbing.The Probability Density Evolution Method for Analysis of Dynamic Nonlinear Response of Stochastic Structures[J].Chinese Journal of Theoretical and Applied Mechanics,2003,35(6):716-722.
[19]LI J,CHEN J B.The Principle of Preservation of Probability and the Generalized Density Evolution Equation[J].Structural Safety,2008,30:65-77.
[20]SOONG T T.Random Differential Equations in Science and Engineering[M].New York:Academic Press,1973.
[21]张涵信,沈孟育.计算流体力学[M].北京:国防工业出版社,2003:134-172.

