铁路客运票额预售控制决策模型研究

刘帆洨， 彭其渊， 梁宏斌， 杨 奎

（1.西南交通大学 交通运输与物流学院，四川 成都 610031；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031）

铁路客运售票组织是铁路旅客运输组织管理的核心，是铁路生产管理工作的重要内容，是影响铁路运输能力和运营效益的关键环节。铁路客运售票组织是一个以票额分配为基础，与多种辅助决策相结合的复杂问题。

既有的票额分配是根据列车运行图，将旅客列车运输能力分配到列车沿途各停靠站的分配计划［1］。票额分配计划是比较成熟的产品［1-4］。然而目前票额发售仍采用“先到先得”的方式，极易导致因短途旅客提前购买，长途旅客需求无法被满足，出现“车上空位，车站没票”。为了合理利用票额，提高列车能力利用率和运输收益，一系列票额分配方法受到关注，成为近年来铁路客运运营管理的研究热点。文献［5］基于客流预测，提出了以旅客列车全程的客座率、收入以及整体效益最大化为目标的票额智能预分方法；文献［6］通过分析客流趋势规律和分布规律，实现了随机需求与随机票额分配的单列车票额分配方法；文献［7］在客流预测基础上，提出票额数量调配模型、席位占用优化模型，并基于这两种模型得到票额分配方案；文献［8］针对高速铁路提出“嵌套式”票额分配模型来保护长途OD的需求；文献［9］结合OD客流需求，提出高速铁路多列车多停站方案的票额分配方法，考虑了同一OD多列车服务的可替代性。以上研究主要根据OD客流的需求预测，将票额提前裂解实现预分，对预售过程中OD需求的变化未给予充分考虑，不利于铁路运输能力的充分挖掘和效益提高。

本文基于列车沿途各停靠站的票额分配计划，研究单列车票额预售控制策略。根据预售期旅客购票趋势规律，将预售期分为不同阶段；以客流需求预测值、最低票额保护值为约束条件，以不同OD旅客在各预售阶段的平均购票强度来描述预售期变化的OD需求，以半马尔可夫决策过程为基础，建立单次决策期望收益模型，并以此推广至列车全程及整个预售期，构建以最大期望票价收益为目标的单列车票额预售控制决策模型；进而获得预售期不同阶段各OD的控制票额，为铁路客运票额控制策略的研究提供一种新思路。最后，运用Matlab进行算例分析，验证了方法的可行性。

1 问题描述

由时序原理可知，预售期的购票需求应存在一定趋势规律；先购票的旅客具有优先的能力占用范围选择，不同能力占用过程的具体表现是各OD旅客在各预售阶段的平均购票强度，因此各预售阶段票额需裂解的数量和程度也不同。现有的票额分配方法未考虑预售期的购票趋势和不同OD的平均购票强度等因素，不利于票额的充分利用。根据旅客购票趋势，对预售期进行阶段划分；结合OD需求变化，限定各阶段不同OD的控制票额；可避免票额未预分导致短途旅客先购票，占用紧张区段的能力致使长途旅客购买不到车票；避免票额被提前预分导致不能更好的适应预售期变化的购票需求。

客票发售过程可以认为是一个有限、离散时段的马尔可夫决策过程［10-12］。马尔可夫决策过程是指决策者周期地或连续地观察具有马尔可夫性的随机动态系统，并序贯地做出决策，即根据每个时刻观察到的状态，从可用的决策集合中选一个做出决策。决策者根据新观察到的状态，再做新的决策，依此反复地进行。但连续时间的观察会导致较高的观测成本，且不能很好地适应时变客流。半马尔可夫决策过程（SMDP）是以每次事件为触发点来做出决策，即各状态转移时刻具有马尔可夫性，其决策过程能充分结合不同OD旅客在各预售阶段的平均购票强度。因此，本文以每次购票请求为触发事件，利用半马尔可夫决策过程来描述单列车票额预售决策过程，得到列车票额预售控制决策链。该决策链是模型构建的基础。

2 预售控制决策链

2.1 参数说明

首先定义如下输入参数：C为列车定员；Z为列车办理旅客乘降作业的车站总数；zi为列车运行起讫点所经停的第i个车站；（i，j）为由车站zi到车站zj的OD区间；T为预售期的第T个阶段；MT为第T阶段包含的发售天数为列车在预售期第T阶段、区间（i，j）的累计售票统计值；tp、tq为预售的第tp、tq天；其中p和q为预售期阶段划分的第p和第q个时间节点，且p ＜q；li，j为列车在区间（i，j）的票额最低保障值；Di，j为列车在区间（i，j）的客流需求预测值；U［tp，tq］为列车在预售阶段［tp，tq］的购票需求预测值；为平均购票强度，表示第T 阶段，区间（i，j）在单位时间（小时）内的平均购票量。

为方便模型描述定义如下变量：ei，j为区间（i，j）出行旅客的购票请求；所有购票请求集合为E，｛eij｜eij∈E｝。sv为第v个购票请求到达时的状态层，每个状态层对应一个或多个不同状态。为决策分析过程中，区间（i，j）的控制票额表示sv状态层，第k决策点对应的当前状态；所有状态集合为S，sv（k）∈S。A为对任意购票请求的所有决策集合为满足购票请求，0则反之。a（ei，j）为对购票请求ei，j的决策；当购票请求到达时，需要从决策集合A中选择一种决策，a∈A。R为累计期望票价收益。

2.2 基于SMDP的预售决策分析

利用SMDP对预售过程进行描述。为方便起见，考虑5个车站、单一席别、无限售车站。z1为始发站，z2至z4为中间站，z5为终点站。假设任意OD区间旅客购票强度服从泊松分布，无旅客退票。每个发售站都可提供多种OD客票产品，例如：发售站z1的客票产品为区间 （1，2），（1，3），（1，4）和 （1，5）的客票。

根据购票统计数据得到任意车次预售期的日购票趋势分布，采用文献［13］的特征识别法，将预售期分成N个阶段（例如N＝3），则T∈［1，N］，阶段划分的时间节点分别为第t0、t1、t2和t3天，见图1。

图1 预售时间的阶段划分

利用现已成熟的时序分析法［13］可得到列车在预售第一天t0至预售期内任意tq的购票需求预测值U［t0，tp］、任意区间（i，j）的客流需求预测值Di，j。而对于可根据统计数据和MT来表达

图2为预售决策流程。令所有ni，j＝0，对任意的｛ei，j｜ei，j∈E｝满足购票请求。当任意一种区间（i，j）的控制票额ni，j达到最低保障值li，j，系统开始决策分析。记第一次开始决策分析时各OD的控制票额为决策分析初始状态s0。

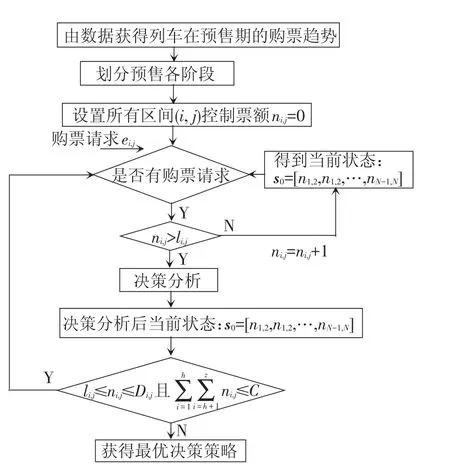
图2 预售决策流程

在决策分析阶段，所有｛ei，j｜ei，j∈E｝可分为两类，一类是不用决策分析，直接满足的请求ei，j，以集合G表示，包括：控制票额未达到区间（i，j）最低保障值的ei，j属于集合G。另一类是需要决策分析的ei，j，以集合H表示，包括：除集合G以外剩余所有区间（i，j）的ei，j，即 H＝E－G。随着满足购票请求次数的增加，集合H最终将包含所有OD区间。

如图3所示，每条虚线代表任意｛ei，j｜ei，j∈H｝到达时生成的状态层sv。每个状态层包含多个节点，每个节点代表经历不同决策过程得到的决策点。决策点内的数字表示所在状态层的决策点编号。每一决策点连接着两条边，分别代表不同决策和状态参数改变情况。决策分析方法为：

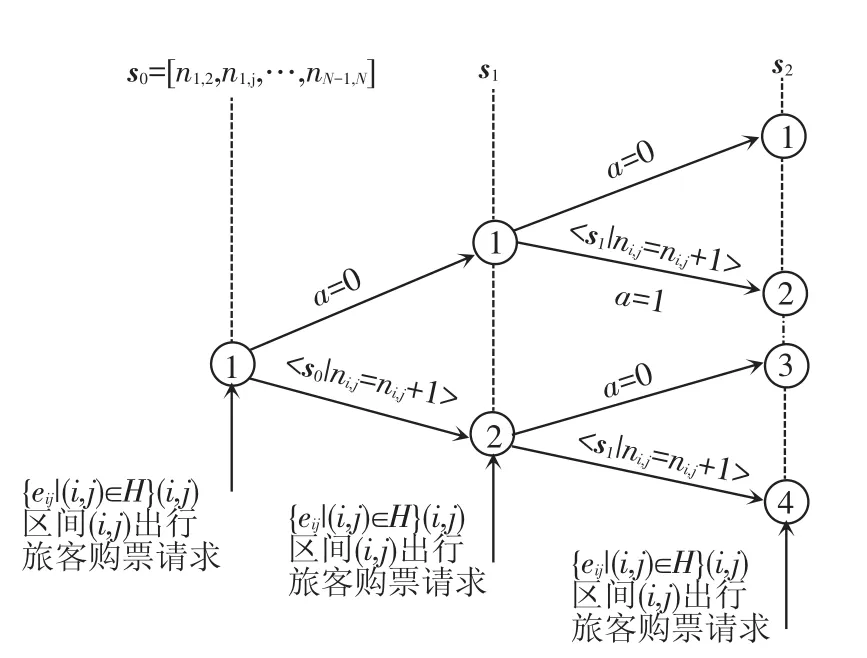
图3 决策分析方法

（1）在决策分析阶段，对集合H 的任意ei，j需做决策分析。对任意sv层的第k决策点，不同决策分析经过不同的状态转移，生成不同的决策点：决策a＝1，当前控制票额ni，j累加1；决策a＝0，当前控制票额不变；其他决策点分析方法相同。

（2）在决策分析阶段，对集合G的任意ei，j直接满足，不做决策分析，没有状态转移，不会生成新的决策点，仅将当前状态层sv包含的各决策点控制票额ni，j更新为ni，j＋1。

（3）当任意sv层的第k决策点的所有控制票额ni，j之和满足式

（4）则该决策点为预售阶段时间节点tq对应的决策点，其状态sv（k）＝［n1，2，n1，3，…，nN－1，N］的各参数为截止到时间节点tq的票额预售控制量；此时，决策点k的平均购票强度由当前变为

对集合H的任意ei，j做决策时，由状态层sv转移至sv＋1。对sv层的第k决策点，a＝1的状态转移概率为满足区间（i，j）旅客购票请求的概率。a＝0的状态转移概率为未满足购票请求的概率。因此，当平均购票强度为时，不同决策的状态转移概率p（sv＋1｜sv）

式中：μi，j和γij是状态转移概率的影响因子。其中，μi，j是出行距离保护系数。结合票额预售原则，需保证长途客票效益，因此状态转移概率还应受到μi，j的影响。μi，j为当前旅客出行距离与列车全程距离的比值，0≤μi，j≤1。出行距离越远μi，j值越大，当μi，j＝1表示始发终到的出行。γij是旅客对区间（i，j）票额的敏感度（购票敏感度）。在实际预售过程中，旅客购票时间大部分比较集中，且存在很多即买即走的旅客，对当前票额余量较敏感；由于短途旅客较长途旅客有更多的出行方式选择，因此长途旅客对票额信息更敏感。由此，定义旅客对区间（i，j）的购票敏感度为包括区间（i，j）所有OD的已售票额总量与列车定员的比值，即

（5）当包含区间（i，j）的所有区间票额的总量达到列车定员时，或当ni，j达到区间（i，j）客流需求预测值Dij时，停止增加该区间的票额。

（6）当所有区间票额停止增加时，决策分析结束，不同决策过程形成多条决策链。

（7）就不同决策链而言，由于对集合G的决策是固定的，由集合G得到的收益也是固定的，因此无需考虑该部分收益对不同决策过程的影响。

3 模型构建

3.1 单次决策期望收益模型

决策分析结束后，需要计算每一决策链的期望票价收益。因此，需要分别计算各决策点的单次决策期望收益。图4，假设区间（1，2）的购票请求到达，发售

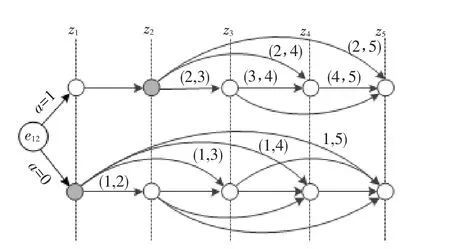
图4 单次决策的期望收益

站为z1：决策a＝1时，裂解站为z2，票额裂解后的剩余席位可形成区间（2，3）、（2，4）、（2，5）、（3，4）、（3，5）和（4，5）六种剩余客票产品，且以一定概率被再次销售。其中，所有剩余客票产品的期望收益称为席位剩余期望收益。因此，单次决策期望收益包含两部分：当前客票产品收益和席位剩余期望收益。决策a＝0时，客票产品收益为0，席位剩余期望收益则是将乘车站z1作为裂解站的剩余客票产品的期望收益。

基于以上分析，推广至Z个车站，有Z（Z－1）／2种不同区间客票产品。令βi，j表示客票（i，j）的票价。由于在计算决策链期望票价收益时，每一条决策链对应每一状态层的唯一决策点，因此在计算时将sv（k）简化为sv。令x（sv，a）表示状态为sv的决策点，对购票请求ei，j做出a决策的客票收益

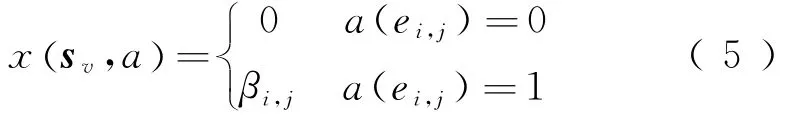
令y（sv，a）为a决策下的席位剩余期望收益

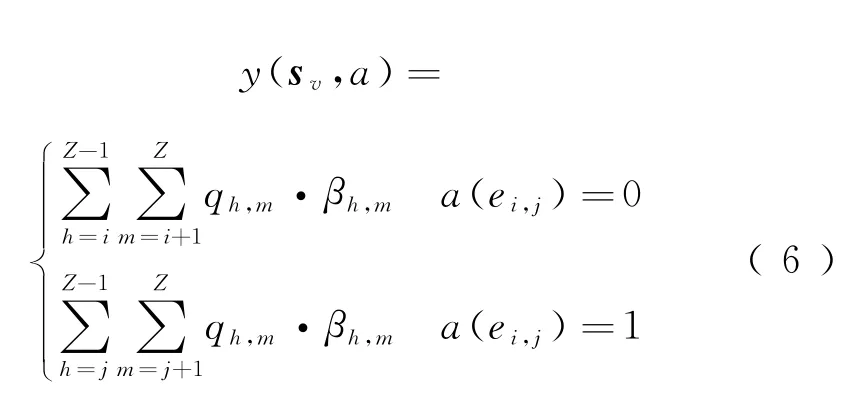
式中：βh，m、qh，m分别为a决策下，区间（h，m）的客票价格和该产品售出概率。记当前平均购票强度为λTi，j，则qh，m

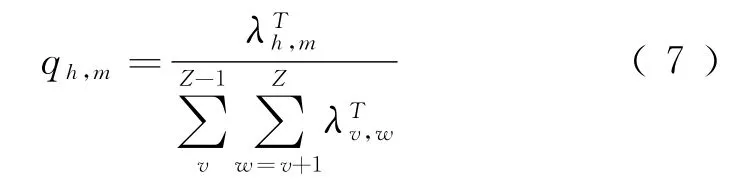
式中：

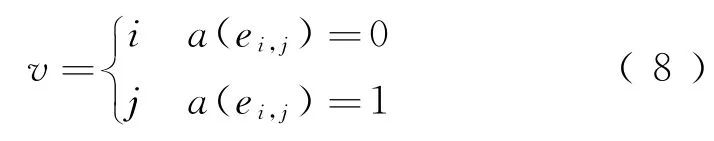
得到单次决策期望票价收益

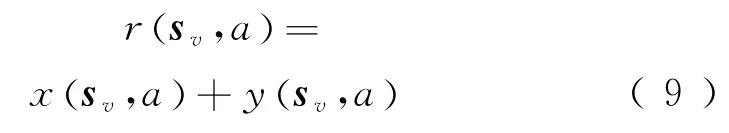
3.2 预售控制决策模型

基于单次决策期望收益模型，建立以最大期望票价收益为目标的票额预售控制决策模型

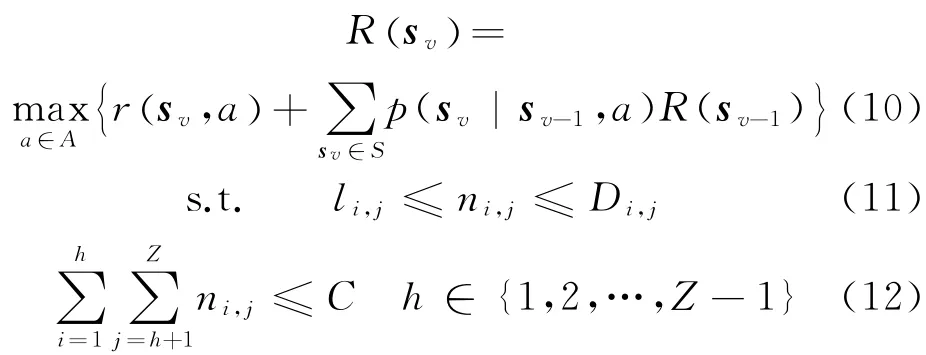
式中：0＜i≤h且h＜j≤Z。式（10）描述了每次新决策后的总期望收益R（sv）与决策前总期望收益R（sv-1）的递推关系：a决策下状态转移至sv的新增期望收益r（sv，a），与前一状态总期望收益R（sv－1）在转移概率p（sv｜sv－1，a）下的期望收益之和，即为新决策后的总期望收益R（sv）。通过迭代计算，最后获得最大期望票价收益对应的决策链。式（11）表示状态sv下，该列车任意区间（i，j）的控制票额应不小于区间（i，j）的票额最低保障值，且不超过区间（i，j）客流需求预测值。式（12）表示任意状态下，包含任意相邻车站区段所有客票产品的控制票额不大于列车定员；即任何时刻，任意相邻车站区段的列车运输总量不大于列车定员。

3.3 获得最优决策策略

决策分析结束后，得到最大期望票价收益决策链，进而得到预售期各阶段时间节点tq对应的决策点，其控制票额ni，j即为预售阶段 ［tq－1，tq］、区间（i，j）的控制票额。

4 算例分析

4.1 预售控制决策策略

以某车次的高铁列车为例，该列车运行线路包含5个客运站z1至z5。车站z1至z4的票额分配为（520，80，10，0）。设列车总定员610，预售时间20 d，各 OD约束条件（客流需求预测值、最低票额保障值、票价）和OD公里数，见表1。考虑单一席别类型（二等座）。

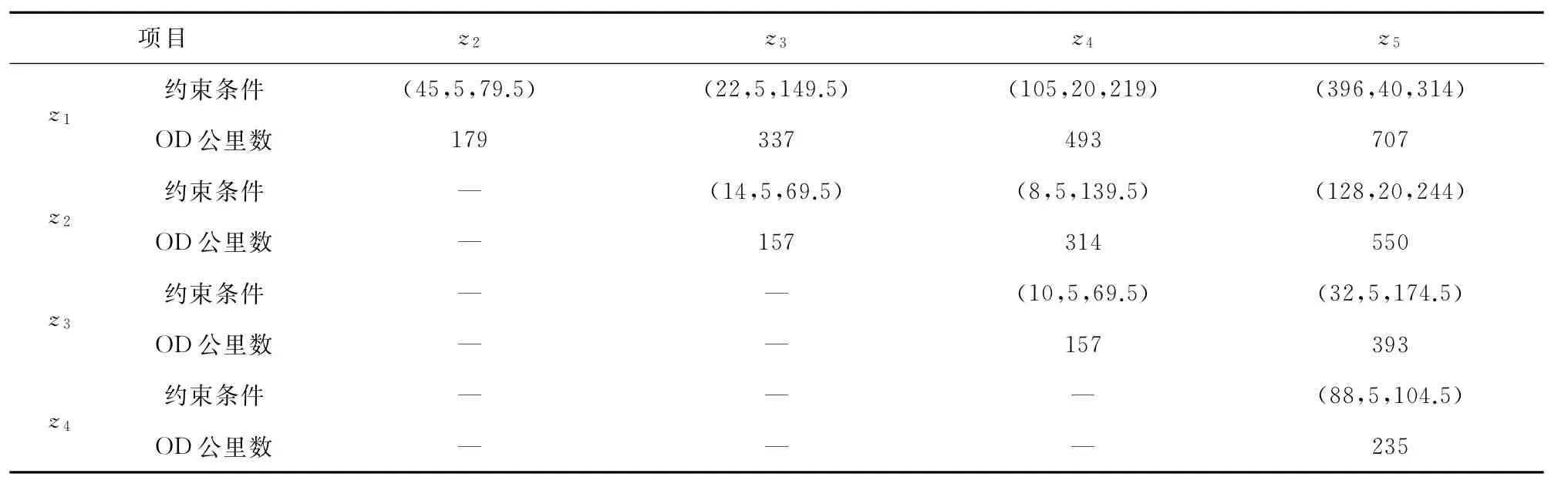
表1 约束条件、OD公里数

通过数据得到预售期的购票趋势，见图5。根据特征识别法，将预售期（20 d）分成3个阶段：T＝1为［－20，－7］、T＝2为（－7，－3］、T＝3为（－3，0］；时间节点为：t0＝－20、t1＝－7、t2＝－3、t3＝0。

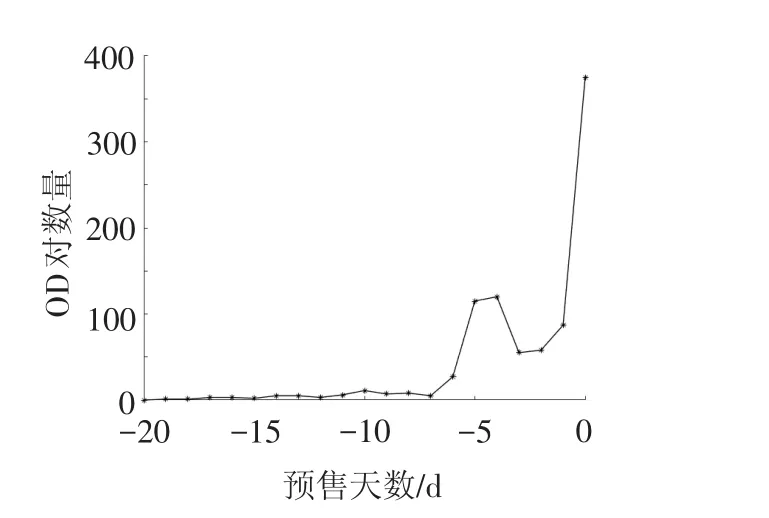
图5 预售期购票趋势分布

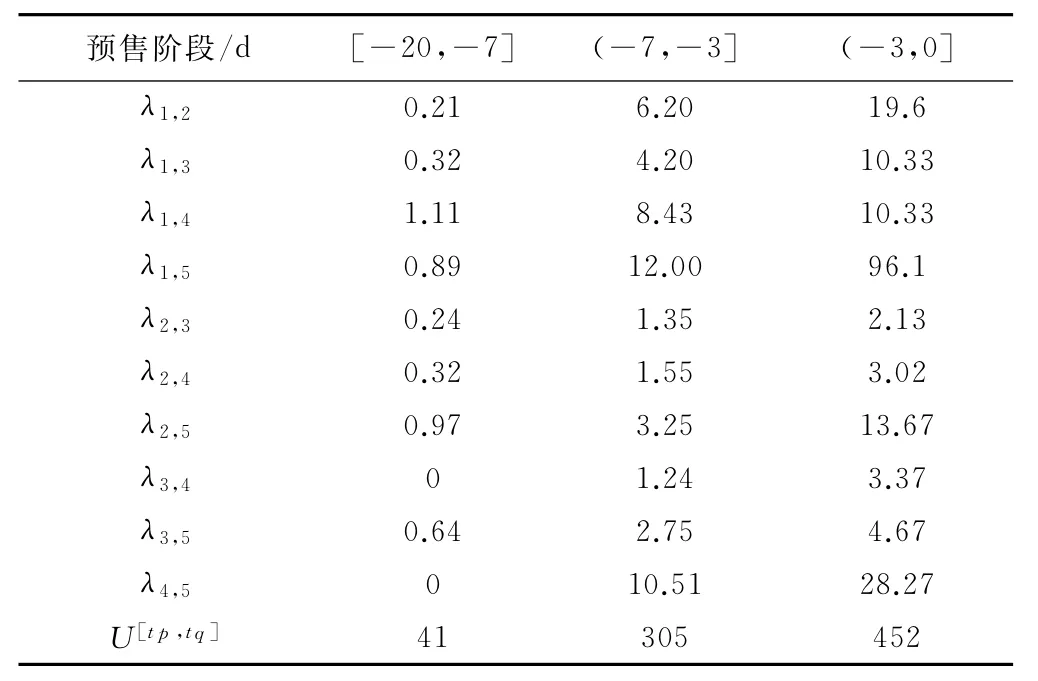
表2 预售期各阶段λi，j与U［tp，tq］

表3 不同预售阶段下各OD的控制票额张

4.2 结果分析

为了分析模型对不同出行距离旅客购票请求的决策影响，将所有OD客票产品按里程区间分为两类短途d1＝［157，337］km 和长途d2＝（337，707］km。根据最优决策链，可得到短途和长途在不同累计售票量下，对新到短途购票请求的决策结果，见表4。

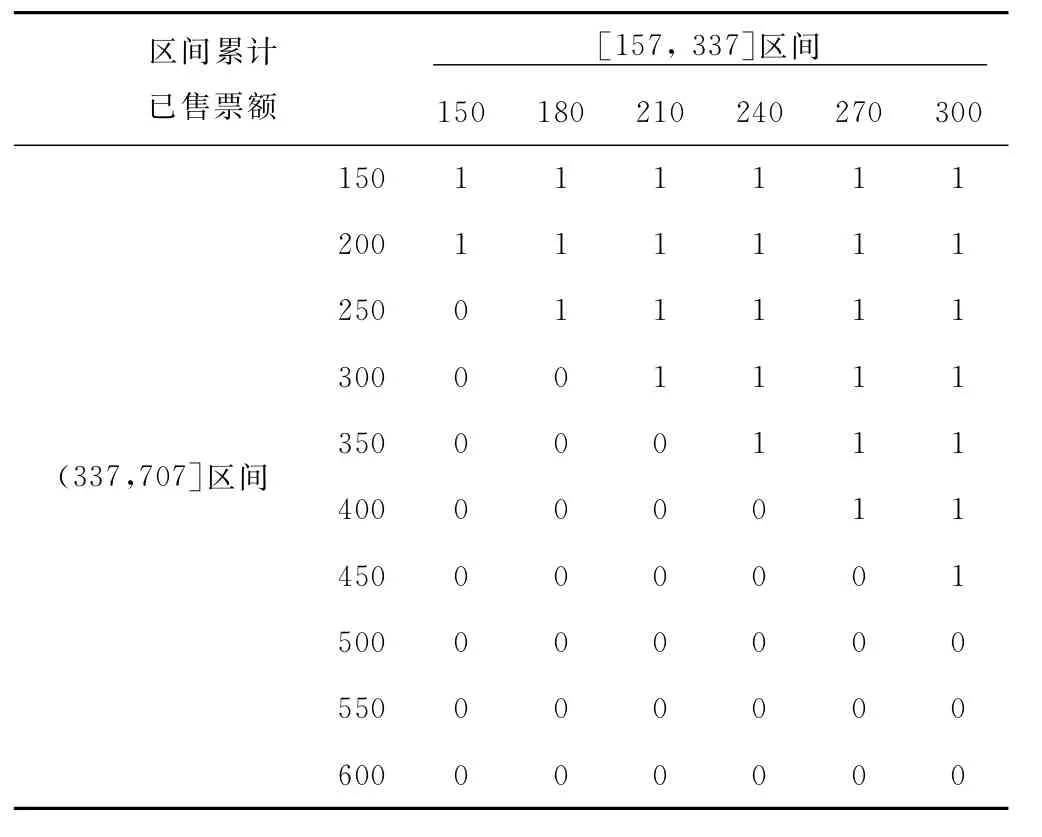
表4 短途购票请求的决策情况

表4中，1表示满足d1里程区段的购票请求；反之则用0表示。随着预售时间的推移，当累计长途售票量逐渐增加，累计短途售票量相对较低时，短途购票敏感度减少，满足短途购票请求的概率较低，有利于保证长途客票效益。另外，当累计短途售票量逐渐增加，累计长途售票量仍较少时，短途购票敏感度增加，满足短途购票请求的概率较高，对挖掘中间站短途客票效益有积极作用。此外，购票敏感度还受到出行距离保护系数影响，随着出行距离减小，保护水平降低，购票敏感度降低。因此，该模型在考虑旅客出行需求条件下，结合出行距离保护系数，可实现对不合理的短途票裂解加以控制，从而提升长途客票效益。

采用贪婪算法（Greedy Model）模拟传统预售先到先得，与预售控制模型进行比较。以区间（1，5）和（1，2）分别代表始发长途与短途，分析不同OD需求的票额预售控制结果。贪婪算法总是会接受优先到达旅客的购票请求，直到达到票额上限值。

如图6所示，随着时间推移，累计售票量增加，且购票需求集中于预售－7 d之后。预售初期，两种模型下始发长途、短途票额预售情况相当。随着预售时间推移，由于预售控制决策模型限制了不合理的短途票额裂解，短途售票量略微减少；此外，采用预售控制决策模型的始发长途售票量得到一定程度的提高。

图7 预售各阶段客座率

如图7所示，采用预售控制决策与传统预售相比。预售初期，两种方式得到的客座率较接近。随着预售时间的推移，采用预售控制决策模型的客座率获得明显改善。

如图8所示，对比两种方法的期望票价收益。预售初期累计售票量较低，两种方法下的期望票价收益相近；当累计售票量达到一定程度时，采用预售控制决策模型能获得更高的期望票价收益。本算例中使用常规服务器，采用贪婪算法每次耗时约2 min；预售控制决策模型每次计算时间约5 min，期望票价收益提高约4.1%。

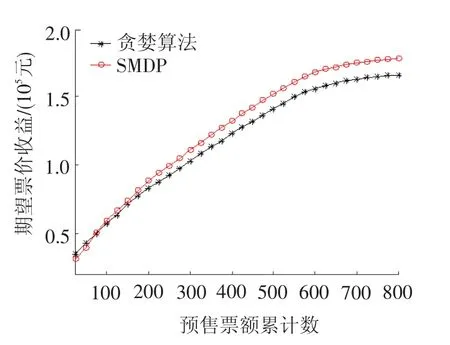
图8 期望票价收益

5 结论

本文在基于列车沿途停靠站的票额分配计划下，以客流需求预测值和最低票额保护值为约束，结合旅客出行需求，充分考虑购票趋势和OD需求变化对列车能力占用过程的影响，基于半马尔可夫决策过程，以期望票价收益最大化为目标，构建了单列车票额预售控制决策模型。该方法可与其他辅助决策（限售、票额共用和席位复用等）相结合。最后通过算例验证了该方法的可行性，并得出：

（1）本文提出方法在考虑旅客出行需求等社会效益的同时，可在一定程度上提高列车客座率和列车运营收益，从而提高列车整体效益。

（2）有利于保证长途客票效益、挖掘中间站短途客票效益。

（3）可有效控制和减少预售期各阶段票额不合理裂解，为铁路客运票额控制策略的研究提供一种新思路。

［1］马建军，许红，胡思继，等.计算机编制旅客列车票额分配系统的理论和设计方法［J］.铁道学报，2001，23（6）：6-10.

MA Jianjun，XU Hong，HU Siji，et al.Theory and Design Method on Seats Allotment System of Passenger Trans Worked out with Computer［J］.Journal of the China Railway Society，2001，23（6）：6-10.

［2］张振利.适应中国高速铁路客流特性的售票组织策略优化研究［J］.铁道经济研究，2010（6）：43-45，50.ZHANG Zhengli.Research on the Optimization of Ticketing Management Strategies According to the Characteristics of Chinese HSR Passenger Flow［J］.Railway Economics Research，2010（6）：43-45，50.

［3］史峰，陈彦，周文梁，等.基于用户平衡分析的铁路旅客列车票额分配计划制定及评价方法［J］.中国铁道科学，2008，11（6）：98-103.

SHI Feng，CHEN Yan，ZHOU Wenliang，et al.Based on User Equilibrium Analysis of the Railway Tickets Allocation Plans and the Evaluation Methods［J］.China Railway Science，2008，11（6）：98-103.

［4］叶建娥，陈光伟.旅客列车票额自动分配系统的设计和实现［J］.中国铁道科学，2003，24（4）：54-58.

YE Jiane，CHEN Guangwei.Design and Implementation of Automatic Seats Allotment System for Passenger Trains［J］.China Railway Science，2003，24（4）：54-58.

［5］单杏花，周亮瑾，吕晓艳，等.铁路旅客列车票额智能预分研究［J］，中国铁道科学，2011，32（6）：125-128.

SHAN Xinhua，ZHOU Liangjin，LÜXiaoyan，et al.Study on Intelligent Advance Tickets Allocation of Railway Passenger Train［J］.China Railway Science，2011，32（6）：125-128.

［6］包云，刘军，刘江川，等.基于随机需求的单列车票额分配方法［J］.中国铁道科学，2015，36（2）：96-102.

BAO Yun，LIU Jun，LIU Jiangchuan，et al.Single Train Tickets Allocation Method Based on Stochastic Requirements［J］.China Railway Science，2015，36（2）：96-102.

［7］王洪业，吕晓艳，周亮瑾，等.基于客流预测的铁路旅客列车票额智能分配方法［J］.中国铁道科学，2013，34（3）：128-132.

WANG Hongye，LÜ Xiaoyan，ZHOU Liangjin，et al.Railway Passenger Tickets Intelligent Allocation Based on Flow Forecast［J］.China Railway Science，2013，34（3）：128-132.

［8］包云，刘军，马敏书，等.高速铁路嵌套式票额分配方法研究［J］.铁道学报，2014，36（8）：1-6.

BAO Yun，LIU Jun，MA Minshu，et al.Nested Seated Inventory Control Approach for High-speed Trains［J］.Journal of the China Railway Society，2014，36（8）：1-6.

［9］赵翔，赵鹏，李博.多列车多停站方案条件下高速铁路票额分配研究［J］.铁道学报，2016，38（11）：9-15.

ZHAO Xiang，ZHAO Peng，LI Bo.Study on High-speed Railway Ticket Allocation under Conditions of Multiple Trains and Multiple Train Stop Plans［J］.Journal of the China Railway Society，2016，38（11）：9-15.

［10］GOASVI A，OZKAYA E，KAHRAMAN A F.Simulation Optimization for Revenue Management of Airlines with Cancellations and Overbooking ［J］.OR Spectrum，2007，29（1）：21-38.

［11］FENG Y，GALLEGO G.Perishable Asset Revenue Man

agement with Markovian Time Dependent Demand Intensities［J］.Management Science，2000，46（7）：941-956.

［12］LAUTENBACHER C J，STIDH AM S J.The Underlying Markov Decision Process in the Single-leg Airline Yield Management Problem ［J］.Transportation Science，1999，33：136-146.

［13］刘强.基于复杂系统的铁路客流预测方法研究［D］.北京：中国铁道科学研究院，2008：41-56.