高速列车转向架蛇行失稳的MEEMD-LSSVM预测模型
叶运广, 宁 静, 种传杰, 崔万里, 陈春俊
(西南交通大学 机械工程学院,四川 成都 610031)
蛇行运动稳定性是高速列车实现安全运行的一个重要问题。由于机车轮对具有一定锥度,即使车辆沿平直的轨道运行,只要有一个初始激励,轮对就会绕轨道中心线边横移边摇头耦合向前运动,即蛇行运动[1]。当列车处于蛇行运动状态时,在速度不变的情况下,若其中一个振型呈现幅值相等的运动状态,此时列车的行驶速度即为该列车的蛇行失稳临界速度[2]。由于列车系统的固有频率与列车运行速度无关,而列车的自激频率会随着车辆运行速度的提高而增加,所以当列车运行速度不断增加,其自激频率接近固有频率时,列车便可能处于共振状态,从而导致其振型的幅值不断扩大,丧失稳定性,即称为蛇行失稳[3]。列车在实际运行过程中,如果发生严重的蛇行失稳,轨道就会受到剧烈的冲击,从而造成线路损坏(见图1),甚至导致列车脱轨。传统避免蛇行失稳的方法是把列车运行速度控制在发生蛇行运动的临界速度以下,但蛇行稳定性影响因素极为复杂,在列车实际运行过程中,其受到线路形状、曲线半径、轮对锥度、轨距、车辆悬挂系统等诸多非线性因素的影响,有可能列车速度在低于蛇行失稳理论临界速度时,列车就会发生失稳现象[4-5]。因此,仅通过控制车速来避免列车发生蛇行失稳这一方法存在诸多缺点。所以,如何预测蛇行失稳的发生并及时控制,是一个急需研究的问题。

图1 剧烈蛇行运动对线路造成的影响[6]
对于蛇行运动的研究,目前国内外取得了大量研究成果,文献[7]提出非线性临界速度计算方法,通过降低车速避免车辆发生蛇行失稳;文献[8-9]通过动力学仿真计算方法研究了车轮磨损、轨道不平顺等因素与列车蛇行运动理论临界速度的关系。为监测失稳现象,文献[10]利用高斯混合模型实现了转向架横向稳定性的实时监测;文献[11]利用多重分型与SVM方法对转向架横向失稳状态进行识别。但关于蛇行失稳预测方面的研究,现有文献鲜有涉及。文献[12-13]通过描述函数法研究列车蛇行运动,提出蛇行失稳的发生经历正常、过渡区振幅增大和发生失稳这一过程。某型列车的大量跟踪实验数据表明,在列车实际运行中,列车发生蛇行失稳时,其经历的过渡状态时间通常大于7 s[14-15],见图2。基于此,本文旨在建立一种模型对过渡状态快速识别来预测蛇行失稳的发生。
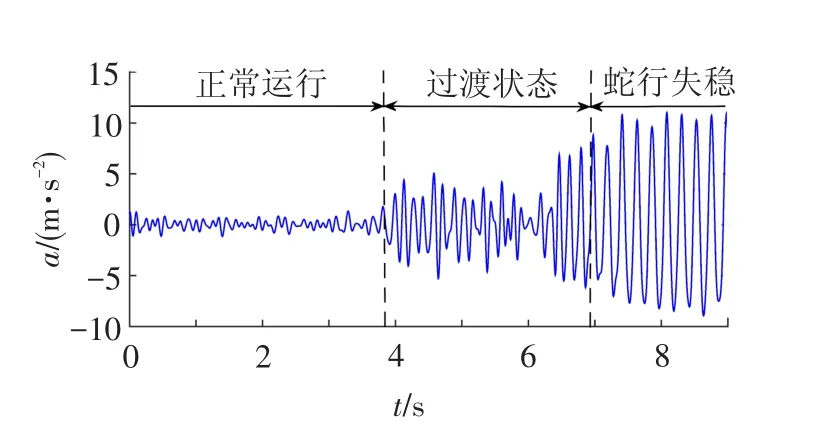
图2 转向架正常、过渡、蛇行失稳3种状态加速度信号
列车从正常状态过渡到蛇行失稳状态时,往往时间较短,只有快速做出预测才能及时对列车进行控制;并且车辆在实际运行过程中,其受到轮轨和悬挂系统非线性因素的影响,导致其走行部运行特性极为复杂,容易产生大量非线性信号。而集总平均经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)被广泛用于此类信号的分析中[16],但该方法会导致白噪声残余,并且通过此方法所得到IMF函数不一定完全符合标准,可能存在模态分裂问题[17-18],改进的集总平均经验模态分解(Modified Ensemble Empirical Mode Decomposition,MEEMD)能解决这些问题;并且,最小二乘法支持向量机(Least Squares Support Vector Machine,LSSVM)较传统的支持向量机(Support Vector Machine,SVM)具有算法简单、求解速度较快等优势[19]。基于以上3种原因,本文结合MEEMD和LSSVM对过渡状态进行识别,从而达到预测作用,实验表明该方法的可靠性和快速性。
1 MEEMD
车辆在运行时,由于自身非线性因素和工况的影响,产生大量的复杂非线性信号,经验模态分解(Empirical Mode Decomposition,EMD)方法被广泛用于分析此类非线性信号,但该方法容易导致模态混叠等问题,为此,Huang提出了EEMD方法。EEMD的原理就是通过向原始信号x(t)添加高斯白噪声,以此来改善非平稳信号的极值点稀疏程度,使其尽可能达到均匀分布状况[16]。EEMD方法可以在一定程度上抑制模式混叠这一缺陷,但是如果添加的白噪声信号幅值过低,信号低频段的极限点稀疏程度就不能被很好地改善,模态混叠问题依然不能被很好地解决;相反,若加入的白噪声信号幅值过高,则EEMD方法的集总平均计算量就会相应变大,并且由于过高幅值的白噪声使得信号高频段的极值点变得更加密集,从而使信号中含有的高频成分很难被分解出来,造成信号中白噪声残余量过大等问题。除此之外,通过EEMD方法所得到IMF函数不一定完全符合标准,也许会造成模态分裂问题。基于以上不足,郑旭,郝志勇等[17]提出了一种能够减少集总平均计算量、解决模态分裂,并且可以减少模态混叠现象的EEMD方法,即MEEMD。对于非平稳信号x(t)的MEEMD分解步骤如下:
Step1把均值等于0的白噪声ni(t)和-ni(t)分别加入到非平稳信号x(t)中,即
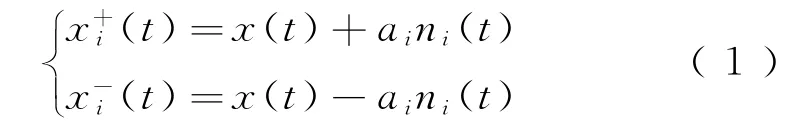
式中:ai为白噪声幅值系数;ni(t)为白噪声,ni(t)与x(t)均方根值应接近。
Step2分别对进行EMD分解,得到IMF分量序列,即
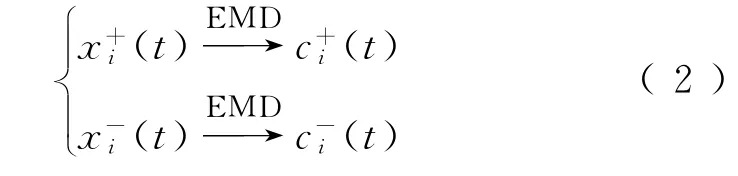
Step3将平均处理,最大可能地消除白噪声残余。
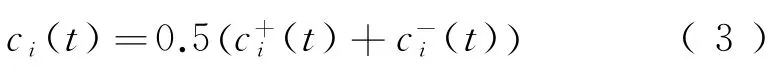
Step4因为ci(t)不一定是标准的IMF函数,其可能存在模态分裂等问题,因此,称其为预本征模态函数,用Pro-IMF表示,然后,再利用EMD方法处理这组分量。
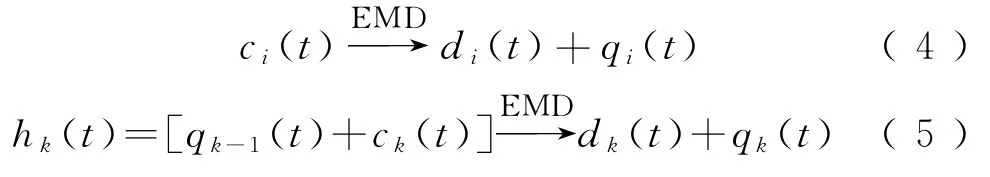
式中:k=2,3,…,m;di(t)为第一个Pro-IMF函数所对应的标准的第一个IMF函数;qi(t)为残余分量;hk(t)为第k个Pro-IMF函数分量;dk(t)为用 EMD方法处理hk(t)所得到的第一个IMF函数分量。
Step5最后MEEMD表达式为
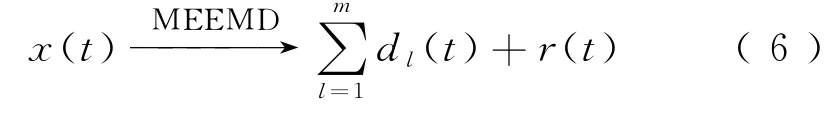
式中:dl(t)为最终IMF函数分量;r(t)为残余函数。
2 LSSVM
标准SVM训练样本时需要求解二次规划问题,训练速度较慢,为解决该问题,Suykens提出了一种新的最小二乘法支持向量机(Least Squares Support Vector Machine,LSSVM)[19],LSSVM 方法的核心即用求解线性方程组代替二次规划问题,从而避免不敏感损失函数,该方法降低运算复杂度,增加运算效率。
其优化问题可表示为
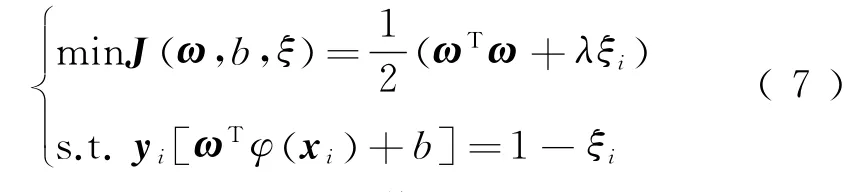
式中:b为偏置;ω 为可调权值矢量;i=1,2,…,n;x为输入矢量;ξi>0为松弛变量,用来度量偏离程度;λ为惩罚因子;非线性变换φ(x)将给定输入样本x映射到更高维的特征空间。约束条件为
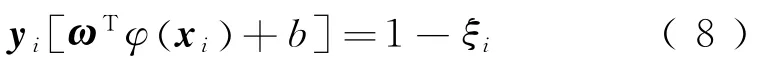
最优超平面分类决策函数
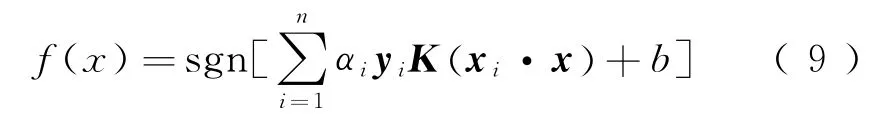
式中:K(xi·x)为满足Mercer定理的核函数。
3 MEEMD-LSSVM蛇行失稳预测方法
由于轨道不平顺和列车系统非线性因素的存在,导致列车运行速度过高时易发生蛇行失稳,蛇行失稳是列车自激频率与其内部某个部件固有频率接近而引起的共振运动,因此蛇行失稳频段下其能量变化必然与正常状态有明显区别[20]。本文首先通过MEEMD对转向架构架正常、过渡、蛇行失稳3种状态下横向振动信号分解得到IMF分量,再计算各个IMF分量的能量,从而构建能量特征矩阵。然后用转向架正常、过渡、蛇行失稳3种MEEMD能量特征对LSSVM进行训练并测试其分类效果,同时,将过渡信号的MEEMD能量特征作为已经训练过的LSSVM的输入特征,评估其计算耗时和识别效果,从而达到预测的目的。该方法流程图见图3。
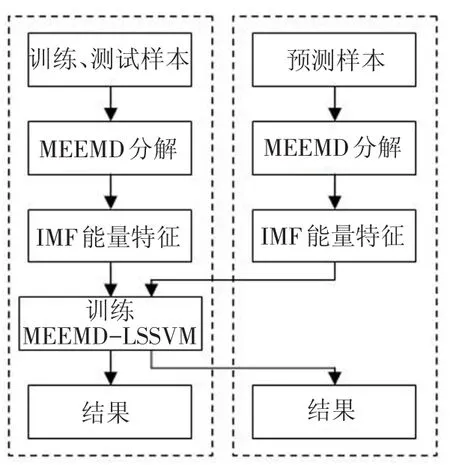
图3 MEEMD-LSSVM分类、预测流程图
其中特征提取方法步骤如下:
Step1分别对正常、过渡、蛇行失稳3种状态下的样本进行MEEMD分解,得到IMF函数。
Step2求得各个IMF函数的能量,由于信号的主要信息被包含在被MEEMD处理后的前几个IMF函数中,并且该文实际分析表明,各个样本被分解后所得到的IMF函数的个数都大于或等于6,为保证该方法的后续性,计算前6个IMF函数的能量Ein,1≤i≤6,n为样本数。
Step3求得的6个能量值构成一个特征向量。

Step4特征归一化处理。
4 试验分析
4.1 试验数据获取
本文所采用的试验数据来源于某线某型号的动车组试验。加速度由列车2车1位转向架构架某型传感器所提供,原始采样频率是2 500 Hz,传感器安装位置见图4。列车的速度信息由车载无线GPS提供,其中转向架构架的单次时间-速度信号和时间-加速度信号见图5,因为车辆蛇行运动频率一般处于2~12.07 Hz范围内,根据香农采样定理和工程经验,用250 Hz对原始信号进行重采样。

图4 转向架传感器安装示意图
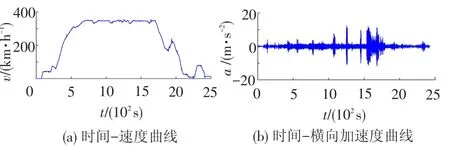
图5 转向架构架时间-速度曲线与时间-横向加速度曲线
据文献[22],当车辆转向架横向加速度信号的峰值连续6次以上(含6次)达到或者超过8~10 m/s2(与转向架的设计相适应)时,即判定为蛇行失稳。文中正常运行状态是指加速度信号的峰值不超过2 m/s2部分[23]。据此分别选取速度在330~350 km/h间时正常、过渡和蛇行失稳3种状态下分别为30、60、30个样本,其中用45个来训练(15个正常运行、15个过渡状态、15个蛇行失稳);45个用来测试(15个正常运行、15个过渡状态、15个蛇行失稳);最后向建立的MEEMD-LSSVM模型输入30个过渡状态样本,计算该模型识别过渡状态样本的计算耗时,并进一步验证该模型的准确性。样本数据过长,会导致采样时间增加和计算量增大;样本数据过短,会导致信息不完整。基于此,通过观察实验数据,结合实际情况,选取样本长度为500个数据点,时间长度为2 s。
4.2 信号的MEEMD分解
对转向架在正常、过渡、蛇行失稳3种状态下的样本进行MEEMD分解,其中一组效果见图6。分析得知,各个IMF函数的频率逐步变低,3种状态下同一尺度的MEEMD处理结果区别明显。
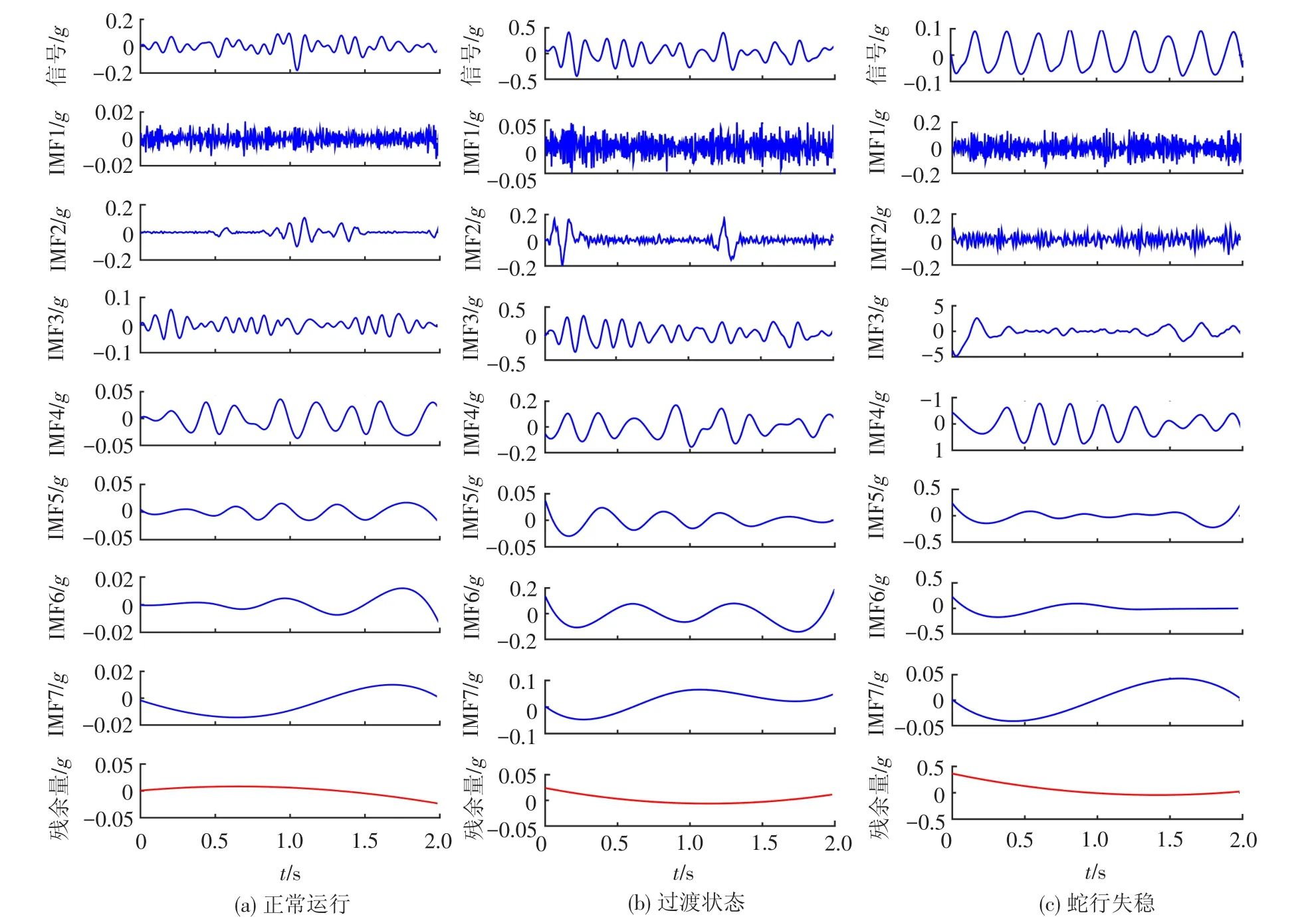
图6 3种状态下信号的MEEMD效果图
4.3 MEEMD-HT时频能特征分析
为展现转向架从正常行驶状态过渡到蛇行运动这一过程的时频能量特征,本文通过MEEMD对转向架在3种状态下的横向振动信号进行分解,再通过H T变换(Hilbert Transformation)得到其时频能量分布特征图,见图7。分析得知,转向架速度在350 km/h时,其正常行驶状态下频率分散分布在0~15 Hz内,能量分布主要集中在频段4~12 Hz,这是因为正常运行时,列车处于随机振动状态,其频率、能量分布分散;过渡状态下,频率、能量分布相对正常行驶时集中,频率分布主要在0~10 Hz内,能量分布主要集中在频段5~10 Hz;蛇行运行时,频率、能量分布高度集中,频率分布在0~8 Hz内,能量分布主要集中5 Hz左右。
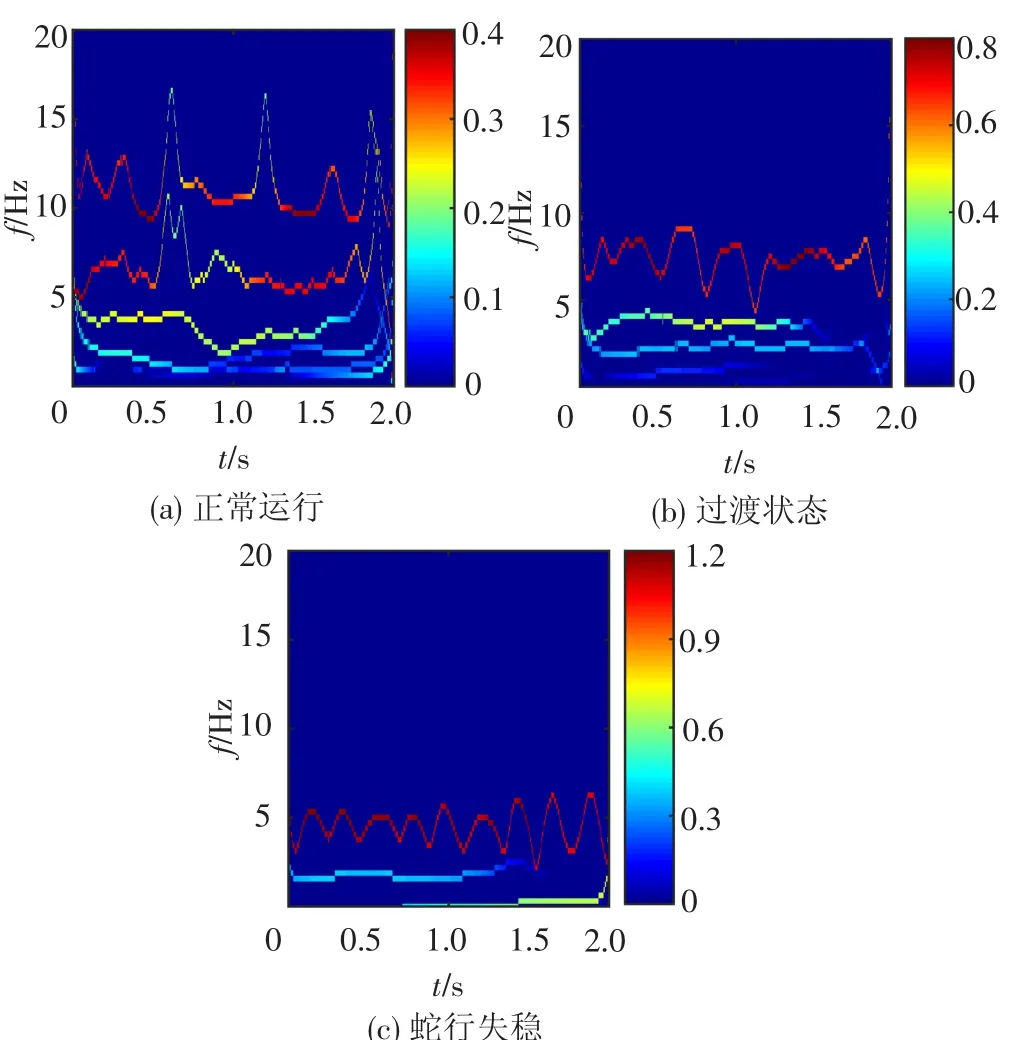
图7 3种状态下信号的MEEMD-HT时频能量分布图
4.4 MEEMD能量特征提取
由4.2节和4.3节得知,转向架3种状态下振动信号经过MEEMD-H T处理后,不同状态下相同尺度的能量分布差异明显,鉴于此,得知MEEMD能量特征是一个能有效识别出不同状态的特征。通过MEEMD对转向架振动信号进行处理,得到IMF函数分量后,计算前6个IMF函数的能量值。表1是列车3种不同状态下2个样本的能量特征值(归一化后)。分析得知,不同状态下的能量分布差异明显,同一状态下的能量分布相似。转向架正常运行时的MEEMD能量值最小,各个IMF函数的能量呈分散分布;过渡状态时的MEEMD能量值介于正常、蛇行失稳之间,其能量主要分布在前3阶IMF函数上;蛇行失稳时的MEEMD能量最大,且主要分布在前2阶IMF函数上。
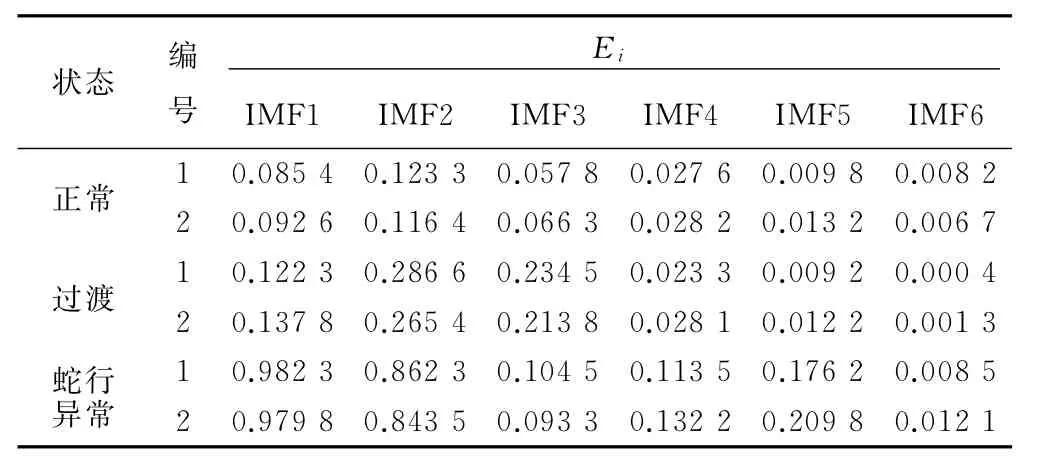
表1 转向架3种状态下的MEEMD能量特征
4.5 训练LSSVM及分类效果
转向架正常、过渡、蛇行失稳3种状态下分别用t=1、t=0和t=-1代表。按照4.1节和4.4节提取能量特征作为LSSVM的输入。采用45个样本进行训练,训练完成后,用45个样本进行测试,并与MEEMD-SVM、EEMD-LSSVM和EEMD-SVM识别结果进行对比,见表2。
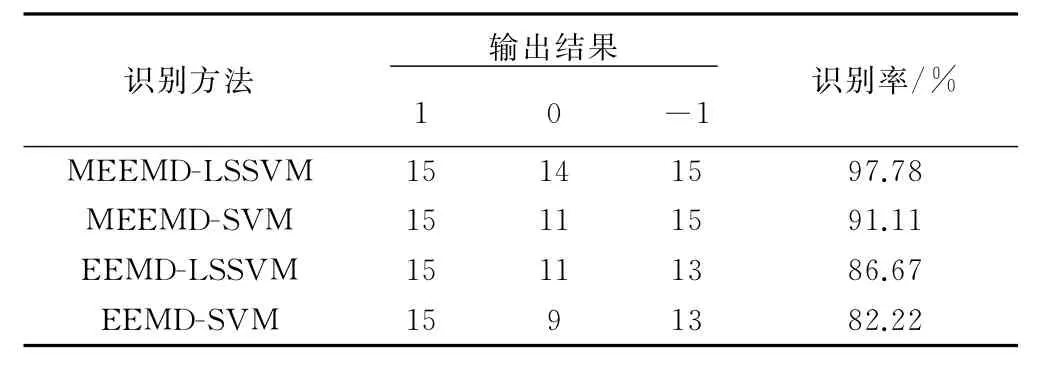
表2 正常、过渡、蛇行失稳3种状态下的正确识别结果
5 结论
针对列车在高速运行状态下容易发生蛇行失稳这一问题,本文从监测数据角度出发,通过建立高速列车转向架的MEEMD-LSSVM的预测模型来对转向架正常行驶和蛇行失稳之间的过渡状态进行识别,从而预测蛇行失稳。结论如下:
(1)MEEMD-LSSVM方法能有效识别转向架正常、过渡、蛇行失稳3种状态。
(2)转向架蛇行失稳的MEEMD-LSSVM预测模型能准确预测蛇行失稳状态,其准确率高于MEEMDSVM、EEMD-LSSVM、EEMD-SVM 预测模型,且计算耗时最短,具有工程应用价值。
由于实验工况的限制,本文只针对某型车速度在330~350 km/h之间时的蛇行失稳进行了分析,提出了转向架蛇行失稳的MEEMD-LSSV M预测模型,对于该方法在不同车型、不同速度下的准确性需要进一步研究,同时,由于列车从正常行驶到蛇行运动状态之间的过渡状态持续时间较短,如何在短时间内及时控制列车,使其安全高速行驶,需要深入研究。
[1]张卫华,李艳,宋冬利.高速列车运动稳定性设计方法研[J].西南交通大学学报,2013,48(1):1-9.
ZHANG Weihua,LI Yan,SONG Dongli.Design Method for Motion Stability of High-speed Train[J].Journal of Southwest Jiaotong University,2013,48(1):1-9.
[2]董浩.铁道车辆运动稳定性及分岔类型研究[D].成都:西南交通大学,2014.
[3]池茂儒,张卫华,曾京,等.蛇行运动对铁道车辆平稳性的影响[J].振动工程学报,2008,21(6):639-643.
CHI Maoru,ZH ANG Weihua,ZENG Jing,et al.Influence of Hunting Motion on Ride Quality of Railway Vehicle[J].Journal of Vibration Engineering,2008,21(6):639-643.
[4]OKAMOTO H,KOTANI M,LIN S,et al.Stabilization Control for Hunting Motion of Railway Vehicle by Gyroscopic Damper(Experimental Analysis Using 1/10 Scale Vehicle Model)[J].Japan Society of Mechanical Engineers,2008,74(2):235-241.
[5]孙丽霞,姚建伟.高速铁道车辆蛇行脱轨安全性评判方法研究[J].中国铁道科学,2013,34(5):82-92.
SUN Lixia,YAO Jianwei.Hunting Derailment Safety E-valuation Method of High Speed Railway Vehicle[J].China Railway Science,2013,34(5):82-92.
[6] KöHLER G, SCHEUNEMANN E, KOLBE T.DieSicherheits Technische Bedeutung Des UIC-merkblattes 518[J].Eisenbahn-Revue International,2003(5):236-239.
[7]TRUE H.Does a critical Speed for Railroad Vehicles Exist[C]//Proceedings of the 1994 ASME/IEEE Joint RaiIroad Conference.New York:IEEE,1994:125-131.
[8]孙善超,王成国,李海涛,等.轮/轨接触几何参数对高速客车动力学性能的影响[J].中国铁道科学,2006,27(5):93-98.
SUN Shanchao,WANG Chengguo,LI Haitao,et al.Analysis of Wheel/Rail Contact Geometric Parameters’Effect on the Dynamic Behavior of High-speed Passenger Car[J].China Railway Science,2006,27(5):93-98.
[9]孙丽霞.高速列车横向运动稳定性和动态脱轨理论分析及评价方法[D].北京:中国铁道科学研究院,2014.
[10]刘峰,延九磊,董孝卿,等.转向架横向稳定性的实时在线监测[J].铁道机车车辆,2010,30(2):5-8.
LIU Feng,YAN Jiulei,DONG Xiaoqing,et al.Real Time On-line Monitor of Bogie Lateral Stability[J].Railway Locomotive&CAR,2010,30(2):5-8.
[11]孙永奎,余志斌,金炜东.基于多重分形与SVM的高速列车运行状态识别方法[J].西南交通大学学报,2015,50(1):7-12.
SUN Yongkui,YU Zhibin,JIN Weidong.Recognizing Running State of High-speed Trains Based on Multifractal Theory and SVM [J].Journal of Southwest Jiaotong University,2015,50(1):7-12.
[12]SOUZA A F D.Influence of the Wheel and Rail Treads Profile on the Hunting of the Vehicle[J].Transact of the ASME,1985,107(1):167-174.
[13]SOUZA A F D,CARAVAVATNA P.Analysis of Nonlinear Hunting Vibrations of Rail Vehicle Trucks[J].Journal of Mechanical Design,1980,102(1):77-85.
[14]林建辉.CRHZ型动车组线路实车脱轨试验车辆测试试验报告[R].成都:西南交通大学牵引动力国家重点实验室,2012.
[15]林建辉.CRH380a-2061转向架蛇行异常振动报告[R].成都:西南交通大学牵引动力国家重点实验室,2011.
[16]ZHAOHUA W,NORDEN E H.Ensemble Empirical Mode Decomposition:a Noise Assisted Data Analysis Method[J].Advances in Adaptive Data Analys,2009,1(1):1-41.
[17]郑旭,郝志勇,金阳,等.基于MEEMD的内燃机辐射噪声贡献[J].浙江大学学报(工学版),2012,46(5):954-956.
ZHENG Xu,HAO Zhiyong,JIN Yang,et al.Study Noise Contributions of IC Engine via MEEMD Method[J].Journal of Zhejiang University(Engineering Science),2012,46(5):954-956.
[18]郑近德,程军圣,杨宇.改进的EEMD算法及其应用研究[J].振动与冲击,2013,32(21):21-26,46.
ZHENG Jinde,CHENG Junsheng,YANG Yu.Modified EEMD Algorithm and Its Applications[J].Journal of Vibration and Shock,2013,32(21):21-26,46.
[19]SUYKENS J A K,VANDEWALLE J.Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[20]YANG Y,YU D,CHENG J.A Rolling Fault Diagnosis Method Based on EMD Energy Entropy and ANN[J].Journal of Sound and Vibration,2006,294(1/2):269-277.
[21]蔡里军.基于FPGA的高速列车转向架蛇行失稳检测装置[D].成都:西南交通大学,2012.
[22]中华人民共和国铁道部.TB/T 3188—2007铁道客车行车安全监测诊断系统技术条件[S].北京:中国铁道出版社,2008.
[23]POLACH O.Application of Nonlinear Stability Analysis in Railway Vehicle Industry[C]//THOMSEN P G,TRUE H.Non-smooth Problems in Vehicle Systems Dynamics.Berlin:Springer-Verlag Berlin Heidelberg,2011:15-27.
[24]刘建强,赵治博,任刚.基于小波包分解和集合经验模态分解的列车转向架轴承智能故障诊断方法[J].铁道学报,2015,37(7):40-45.
LIU Jianqiang,ZHAO Zhibo,REN Gang.An Intelligent Fault Diagnosis Method for Bogie Bearings of Train Based on Wavelet Packet Decomposition and EEMD[J].Journal of the China Railway Society,2015,37(7):40-45.
[25]NING J,LIN J,ZH ANG B.Time-frequency Processing of Track Irregularity in High-speed Train[J].Mechanical Systems and Signal Processing,2016,66/67:339-348.
[26]叶运广,宁静,种传杰,等.基于MEEMD-HT的高速列车转向架蛇行失稳特征分析[J].中国测试,2016,42(9):120-125.
YE Yunguang,NING Jing,CHONG Chuanjie,et al.A-nalysis of High-speed Train Bogie Hunting Instability Based on Modified Ensemble Empirical Mode Decomposition and Hilbert Transformation[J].China Measurement&Test,2016,42(9):120-125.

