不确定条件下铁路应急资源调度多目标优化方法研究

汤兆平， 秦 进， 孙剑萍， 牛 丰，3

（1.中南大学 交通运输工程学院，湖南 长沙 410075；2.华东交通大学 信息工程学院，江西 南昌 330013；3.中国铁路总公司 办公厅，北京 100844）

应急资源调度一般是指突发事件发生之后，将应急资源供应点（可出救点）的应急物资分派到各事故点（需求点）参与救援的一项特殊物流活动，属于应急管理救援体系中响应阶段的关键环节，也是快速、有效实施应急救援的重要保障。当重大的事故或灾难发生时，往往需要多个出救点组合参与救援行动。

随着我国铁路路网建设的高速发展，路网密度越来越大，行车组织越来越复杂，运行速度越来越快，路网多地同时发生突发事件的可能性也相对较大，如遇到地震、台风、山体崩塌、泥石流等大规模自然灾害时，更易造成同一区域路网内出现多处突发事故。因此研究多需求点、多出救点、多资源的应急资源调度优化方法显得更有必要。

目前的相关研究多是针对单一需求点救援［1-7］。当多个地点同时发生应急事件时，由于需求点的路网地位、列车等级、客货损伤以及线路与设施损毁程度不同，各需求点救援的轻重缓急也会有所差异。因此有必要对需求点进行优先级排序，确保重要主干路网或涉及旅客生命安全的重大事故优先救援。

Duan［8］提出了按照事故的危险程度确定救援工作的先后顺序。Cao等［9］提出了灾害重点区域优先救援的歧视模型。郎坤等［10］利用模糊可变集合理论来求解应急物资调度优先排序问题。李磊等［11］将案例推理方法应用到铁路应急决策中，基于铁路事故与既有事故案例的属性相似度来确定最优应急资源调配方案。舒其林［12］建立基于证据理论的优先权排序模型，给出多需求点资源的优先调度策略。周德群等［13］通过层次分析法确定各个需求点的优先权。Sheu［14］和王东海等［15］利用TOPSIS模型进行救援优先权分级，并将优先权以系数形式加入模型，对应急资源进行调度优化，对于合理分配资源、提高救援效率具有很好的借鉴意义。

事实上，由于受灾初期信息的收集多具有不完整性，应急救援调度决策也面临着很大的不确定性，因此有学者引入不确定性方法进行应急资源调度方案的研究。如尹辉［16］考虑道路拥堵、资源需求、决策者偏好等不确定性因素，建立了模糊优化调度模型。王婧［17］基于随机路径时间和模糊需求量，建立了应急时间与成本的多目标模糊随机优化模型。常建鹏等［18］基于前景理论和模糊多指标风险群决策方法，研究确定最优应急方案。Belmont［19］提出了基于模糊集合理论研究应急资源调度问题的方法。高学英［20］解决了应急资源需求估计中的不确定性问题。徐艳艳［21］研究了区间形式的运输时间与费用、随机物资需求下的应急物资调度优化模型的构建及求解方法。

本文在既有研究基础上，采用模糊理论方法和基于熵值客观权重的灰色关联理想方法，对多需求点的救援优先级进行排序，建立了多出救点、多需求点、多资源的调度时间最短、应急费用最低的铁路应急调度多目标优化模型，并基于TOPSIS方法和限定参数区间搜索，设计了帕累托最优解搜寻算法进行问题的计算和分析。

1 问题描述及分析

本文所研究的问题可以描述如下：在规划期内，所研究的铁路区域内，共有J个可能的事故需求点E1，E2，…，EJ，以及I个应急出救点S1，S2，…，SI。在应急出救点Si（i＝1，2，…，I）上储备的第k（k＝1，2，…，K）种应急资源的数量为当需求点Ej（j＝1，2，…，J）上发生事故时，其对第k种应急资源的不确定需求由模糊数确定。出救点Si至需求点Ej所需的时间记为tij，第k种应急资源的单位应急成本为当区域内多个事故点同时提出救援申请时，决策者需以应急资源调度时间最短和应急总费用最小为目标，以确保主干线或重大事故的优先救援为前提，确定最优调度方案。

不确定条件下应急资源调度优化问题的难点之一就是不确定信息的度量与处理。本文研究中所涉及的不确定信息，主要包括专家对各需求点的优先权评价、需求点的资源需求量和应急调度时间。考虑到事故初期信息的不完整，评价专家对各项指标的不同属性及不同指标对优先级的影响程度把握上的差异以及评价语言的模糊性等特点，本文拟采用模糊理论来描述这些不确定性参数。

定义φ为整体应急救援调度方案，φk表示相应的第k种资源的调度子方案。应急资源调度时间表示将所有应急资源送达所有应急需求地点所需花费的最大时间，且t（φ）和t（φk）分别表示整体调度方案φ和子方案φk的应急资源调度时间，则相应的数学表达为

在应急救援调度方案φ中，第k种资源的调度子方案φk可表示为如下矩阵

在进行优化决策时，由于应急需求点的实际需求为不确定量，因此也均为未知量。在模型求解时，必须首先根据事故点的优先级和实际需求量确定

事故点资源分配的优先级可通过建立三角模糊数评价矩阵进行计算确定。同时，考虑到需求点上分配资源量过少会导致救援力量不足，分配过多会导致资源浪费的特性，对应急需求点Ej引入其第k种资源分配满意度函数，并设置为如图1所示的梯形模糊数。

图1 资源调度数量满意度函数

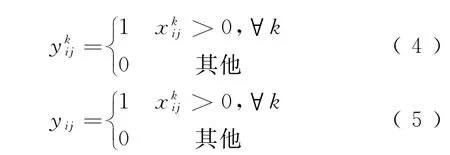
根据定义，则有

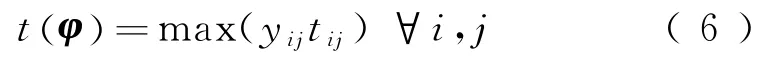
2 优化模型的建立

2.1 不确定需求的去模糊化

如前所述，为了求解模型，需要首先求解需求点Ej对第k种资源的实际分配量xkj。这里将首先对需求点的模糊需求量进行去模糊化处理，得到需求量的确定值，在此基础上依据优先规则计算并分配各需求点的实际资源调度数量。

模糊多目标规划问题，一般需将含模糊参数的模糊规划转化为确定性目标规划问题以方便求解。去模糊化常用方法有截集、模糊模拟、期望值以及无差异曲线等。本文不确定条件下铁路应急资源调度优化问题模型，其中的梯形模糊数需求量，考虑到其系统复杂度及控制精度等因素，选用α截集方法实施去模糊化，并以α截集的重心xkj（α）取代模糊需求量

式中：α为截集的阈值或水平，α∈［0，1］。α的取值越大，不确定程度就越高。令L（α）和U（α）分别为α截集的最小值和最大值，计算为

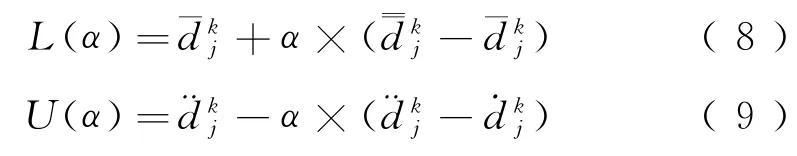
2.2 多目标优化模型的建立

应急救援方案的首要优化目标，显然应是尽可能在最短的时间内将救援设备运送至需求点，即应急资源调度时间应最短，具体为

在满足应急调度时间最短的同时，仍期望应急救援总费用最小，根据前面的变量定义，相应的优化目标函数为

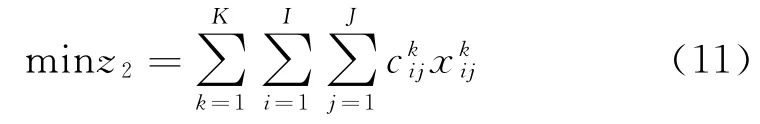
由此，不确定条件下铁路应急资源调度的多目标优化模型为

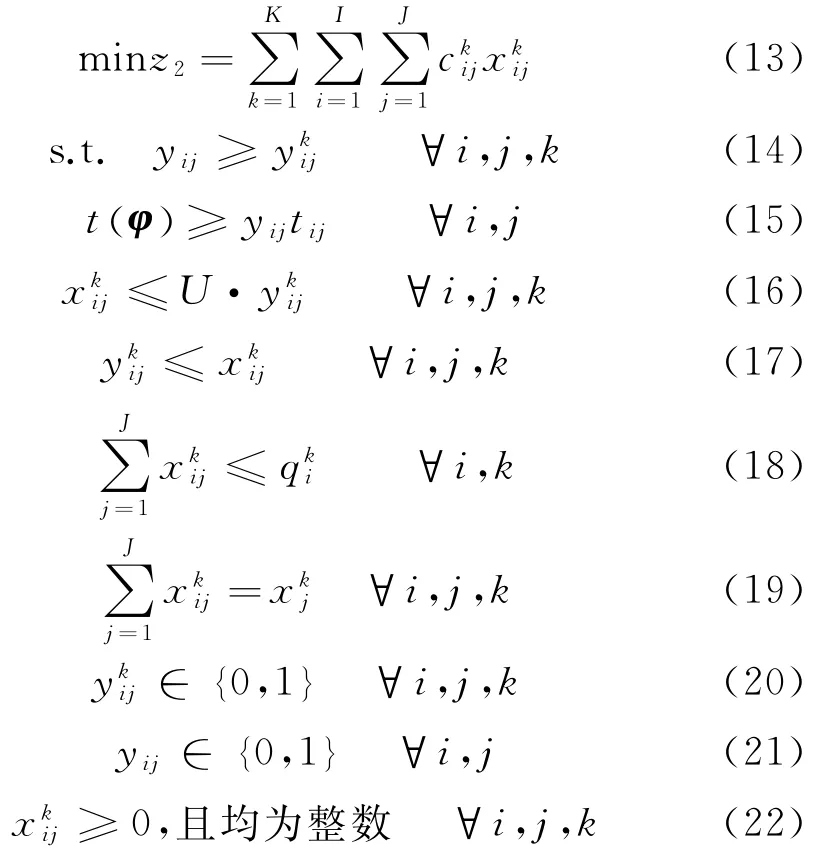
其中，U为任意大的正数。优化式（12）为应急救援的资源调度时间最短，式（13）为应急救援的总费用最小。式（14）为出救点是否对需求点进行了救援；式（15）为资源调度时间t（φ）为应急方案φ中资源到达应急需求点所花费时间的最大值；式（16）、式（17）是确定与之间的逻辑关系，式（16）为若出救点Si对需求点Ej提供的第k种资源的数量，则式（17）为一旦当出救点Si参与对需求点Ej救援，即＝1，既然出救点Si对需求点Ej提供了第k种资源的物资量，则必须大于等于1；式（18）为出救点派出的任一应急资源量，应不大于该出救点拥有的资源备有量；式（19）为任意需求点得到的实际应急资源的计算公式；式（20）～式（22）为决策变量的取值约束。

3 求解方法

一般而言，多目标优化模型的求解存在较大困难，通常需要在多个目标之间进行协调处理，并在所有非劣解中进行择优，以实现各单目标解的最佳均衡。

本文首先使用模糊评价对各应急需求点进行优先级排序，据此确定各需求点的资源分配量后，利用MATLAB的Intlinprog软件包分别求解两个优化目标下的最优解。在此基础上设计了一种限定参量区间的最优解快速搜索方法，并依据对搜寻到的有限个帕累托最优解与理想化目标的接近程度，确定多目标规划问题的最优调度方案。

3.1 救援优先级模糊评价

当多个需求点提出资源的请求时，由于资源的有限性，须按一定规则进行资源分配，以确定每个需求点应被分派到的各种资源数量。本文将遵循当前铁路部门的实际救援原则，在确定事故优先权的基础上确定应急资源的优先分配策略，有利于重大事故和主干线的优先救援。

传统赋权的模糊矩阵评价法虽通过专家集体确定权数，对主观因素进行了一定程度的控制，但仍无法从根本上排除其影响。本文采用的模糊矩阵评价中，运用熵值客观赋权的方法，以各个样本的实际数据求取权重，以避免人为因素影响，获得较高的再现性和可信度。通过数据归一化处理后，还可获得单调性、缩放无关性和总量恒定性等优异品质以及较好的鲁棒性。

本文构建三角模糊数矩阵评价各需求点救援优先级指标。综合运用模糊理论方法、熵值客观赋权、灰色关联和理想解法，构造一种优势互补的相对贴近度决策方法，以有效解决混合型多属性决策的需求点救援优先级排序问题。具体流程如下：

对矩阵A中的元素

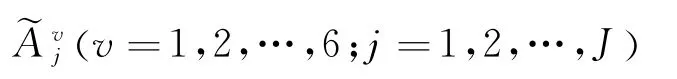
（2）对矩阵A去模糊化处理，得到评价确定型矩阵P。

（4）定义第v个指标的熵值

则第v个指标的客观权重ωv为

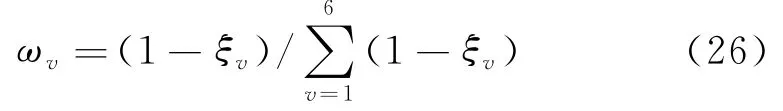
（6）确定理想解H＋与负理想解H－。

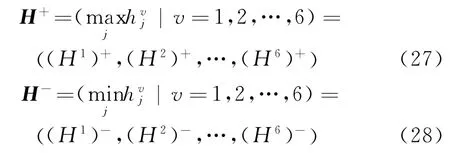
（7）需求点Ej的第v个指标与正理想解的灰色关联系数计算如下

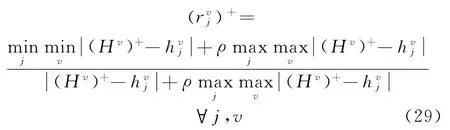
式中：ρ为分辨系数，通常取0.5。计算需求点Ej与正理想解的灰色关联度B＋

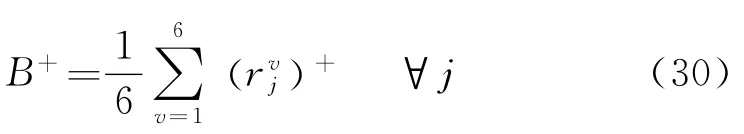
（8）同样的，需求点Ej的第v个指标与负理想解的灰色关联系数计算为

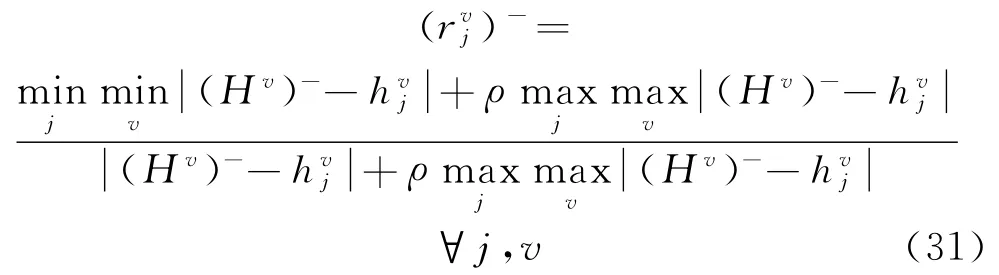
计算需求点Ej与负理想解的灰色关联度B－

（9）计算各需求点的灰色关联相对贴近度Bj。

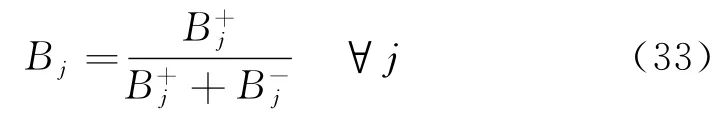
（10）按照灰色关联相对接近度的大小排序：Bj值越大，表示需求点Ej对资源需求的优先级越高；反之，则优先级越低。

3.2 多目标模型的非劣解择优

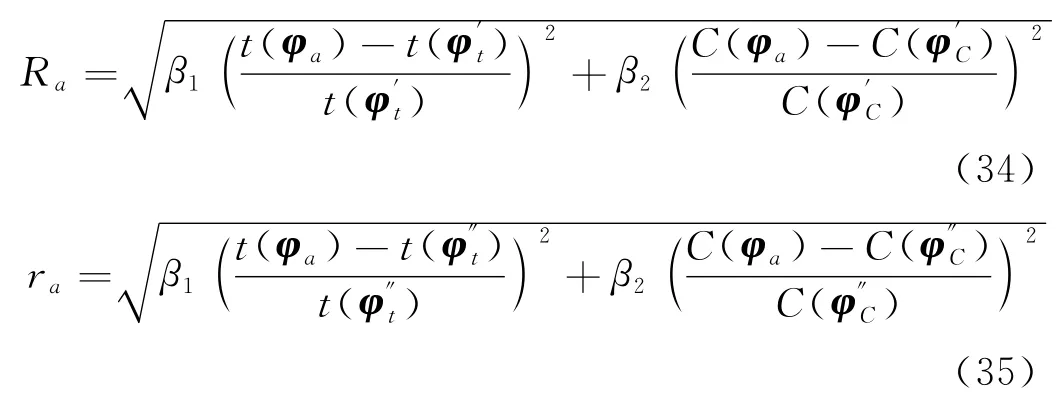
式中：β1、β2分别为关于应急调度时间和应急总费用的权重，β1＋β2＝1。

根据TOPSIS方法，方案φa对理想点的相对接近度εa为

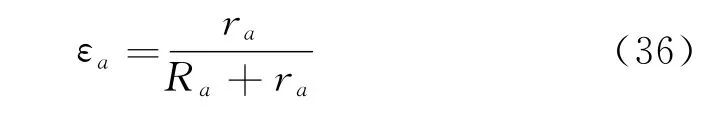
相对接近度εa越大的方案越优。

3.3 限定参数区间的帕累托最优解搜寻算法

非劣解是满足帕累托最优条件的解集中的向量。多出救点、多需求点、多资源的应急资源调度问题属于具有复杂、不连续的帕累托前沿的多目标优化问题，其非劣解的数量，将随系统内出救点、需求点和资源种类的增加而呈几何级数增长。为有效减少求解运算量，本文提出一种限定参数区间的帕累托最优解搜寻方法。

考虑到救援调度时间的取值一般较总费用取值要少，故选择调度时间为限定参数。若限定调度时间不超过某值，则定义该值为限定调度时间，用¯t表示。设调度时间单目标模型最优解对应的最短调度时间为，费用单目标模型最优解对应的最短调度时间为故可将非劣方案的调度时间限定在闭区间因为是实际不可行的方案，而的方案的费用，一定不低于费用单目标模型最优解，显然也较之更劣。故依次限定调度时间最短为时，令xij＝0（即不允许出救点Si对需求点Ej救援），并将该约束加入费用单目标模型。求解且费用最小的非劣解，确保得到的帕累托最优解均在帕累托前沿，并通过与理想点的相对接近度确定最优方案。

限定参数区间的帕累托最优解搜寻算法，其非劣方案的求解次数为tij的取值范围，考虑到因此在求解大规模问题时，能极大地减少最优解的搜寻次数。

4 实例分析

4.1 实例概况

假设某铁路区域受自然灾害影响，多处线路中断，沿线设施破坏严重，途经的列车车体受损，客货受到不同程度伤亡与损失，需要紧急救援及抢修。此次重大突发事件有E1、E2、E3和E4共4处需求点；可由附近的S1、S2、S3和S4共4个可出救点实施救援，每个需求点都需要救援起复设备和简易台车两类应急救援设备资源。

考虑到自救能力不同，以及需求点的地理环境、气候条件、受损结构、受灾规模等因素造成救援难度的差异，根据专家经验，设定本实例下两种资源的模糊需求量。它们的调度时间与单位资源应急费用情况见表1、表2，表中的数据格式为：调度时间（单位资源应急费用）。

表1 第1种资源的调度时间与单位资源应急费用

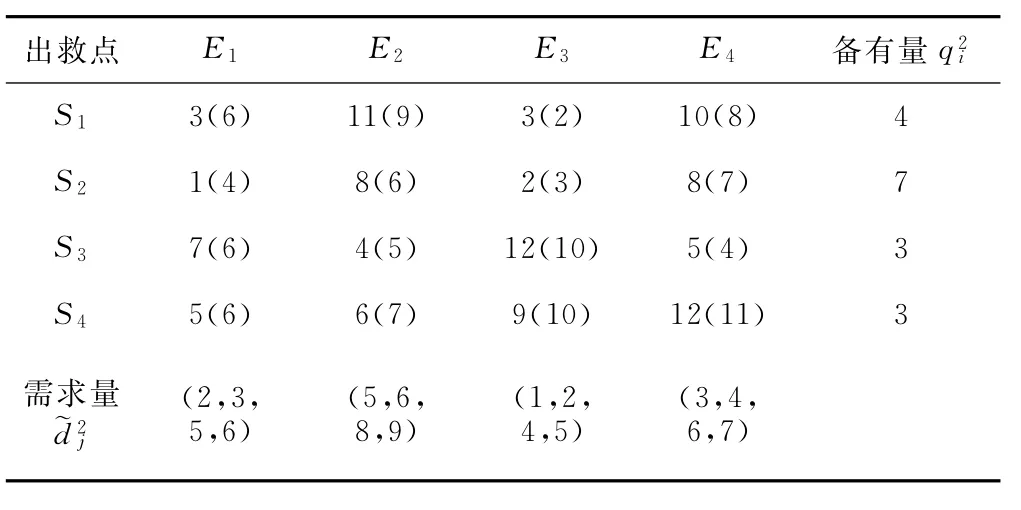
表2 第2种资源的调度时间与单位资源应急费用

4.2 救援优先级的确定

按照3.1节中的步骤，对4个需求点的救援优先级进行计算和排序：

（1）组织专家对4个需求点的6项评价指标进行打分，以三角模糊数形式给出，分值越大，则线路等级和列车等级越高、灾害规模越大、线路损毁程度和人员伤亡程度越严重、自我救援能力越差。由此构建模糊评价矩阵A

（2）以α＝0.5的截集期望值，对评价矩阵A去模糊化，并进行规范化处理，据此计算评价指标的熵值δ和客观权重ω。

（4）分别计算正理想解H＋与负理想解H－为

（5）计算需求点与正、负理想解的灰色关联度及灰色关联相对贴近度。

（6）由此，4个需求点的救援优先权从高到低依次为E1、E2、E4、E3。

4.3 需求点需求量的确定及资源分配

设置截集的阈值α＝0.5，由此可根据式（7），分别计算需求点E1、E2、E3和E4对第1种资源需求量的重心值，分别为3、6、5和6，需求总量为20，同样，对第2种资源需求量的重心值分别为4、7、3和5，需求总量为19。

由表1和表2可知，出救点S1、S2、S3和S4对第1种、第2种资源的备有总量分别为18和17。两种资源的备有总量均不能充分满足所有需求点，因此需根据事故优先级确定各需求点的资源实际分派量。根据上述优先权级的排序，E1、E2和E4优先获取资源并满足需求量。对于E3，第1种应急资源将缺额2个单位，第2种应急资源缺额2个单位。两种资源具体分派情况见表3。

表3 各需求点两种资源的需求量与分配量

4.4 调度方案求解与结果分析

（1）最优与最劣解的求解

①根据需求点优先级计算出来的资源分配量（表3），利用 MATLAB2014B的求解函数Intlinprog，对调度时间单目标模型求解得到最优解φ′t（以下称方案1）

方案1的应急资源调度时间为t＝8，最小总费用C＝190。

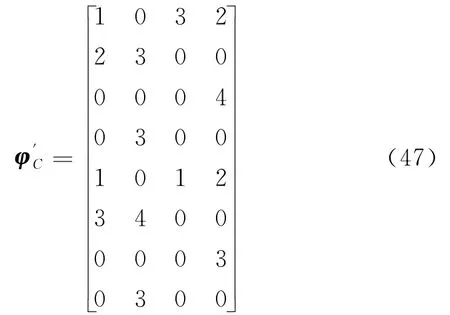
方案2的总费用为C＝181，调度时间为t＝10。

③ 将总费用最小模型中的优化目标，由求取最小值改成求取最大值，得到总费用模型的最劣方案φ″C

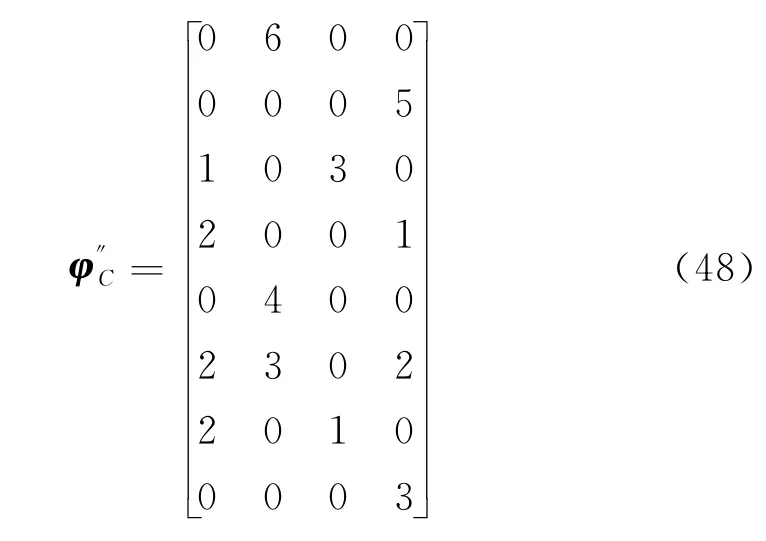
该方案总费用为C＝282。同时该方案的最短调度时间为t＝12。

（2）限定参量区间的非劣方案寻找与择优

根据计算结果，可知调度时间单目标及费用单目标模型的最优解对应的调度时间分别为8和10，即¯t1＝8，¯t2＝10，故将非劣方案的调度时间¯t限定在闭区间［8，10］，表1、表2中，tij∈［8，10］区间的有8、9、10共3种时间，故本文中可以限定调度时间范围为¯t＝8，9，10，即仅需搜索3次非劣方案。

①限定调度时间¯t＝8与¯t＝9，计算结果相同。得到非劣解中的帕累托最优解（以下称方案3）

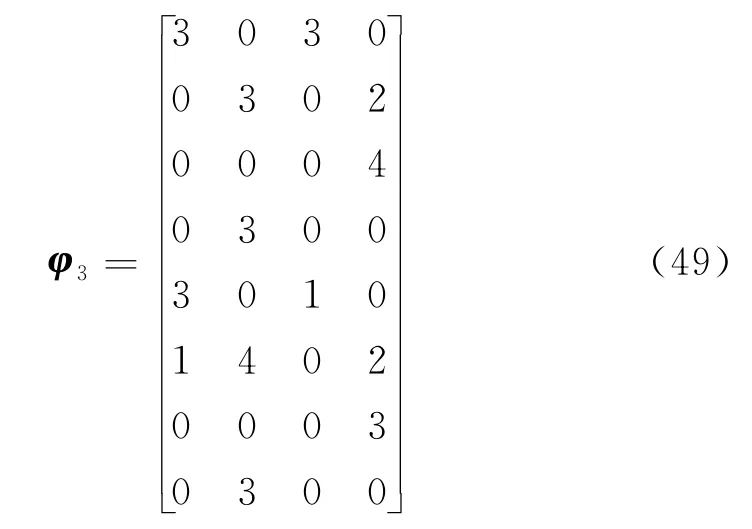
方案3的最短调度时间t＝8，最小总费用为C＝185。

②限定调度时间¯t＝10，该组非劣解中的帕累托最优解与方案2相同。

由此可知，不同方案下的单目标下的最优目标值见表4。

表4 不同方案下的单目标优化值

（3）最优方案的判定

考虑到应急调度时间对于铁路救援的至关重要，给定调度时间的权重β1＝0.65，应急总费用权重β2＝0.35。

根据式（34）～式（36）分别计算不同方案与正、负理想点的接近度Ra和ra，以及理想点相对接近度εa，见表5。

表5 不同方案理想点接近度

由此，经比较分析可判定，最优应急资源调度方案为方案3。

经过比较和分析可以发现，方案3同时考虑了应急资源调度时间件最短和应急总费用最小。相对方案1，方案3在总费用上有2.7%的节约；相对方案2，方案3在调度时间上有25%的节省，在总费用上有2.2%的溢出。因此相对而言，方案3在总体上有更好的优越性。

5 结束语

科学、合理、快速的铁路应急资源调度，是有效降低铁路突发事件损失程度的重要措施。本文针对多需求点、多出救点、多资源的不确定性铁路应急资源调度问题，在对三角模糊数评价矩阵去模糊化的基础上，使用灰色关联理想解方法确定应急需求点优先级，以确保重要需求点的资源需求优先满足。利用模糊理论与方法，处理铁路应急救援中的不确定需求，建立了以应急资源调度时间最短、应急总费用最小为优化目标的不确定条件下铁路应急调度多目标决策模型，并基于TOPSIS方法和限定参数取值区间的帕累托最优解搜求法，设计了求解算法进行模型的计算与分析。

最后的算例计算分析表明，本文所提出的不确定条件下铁路应急调度多目标决策方法，模型符合实际需求，算法求解迅速，结果科学合理，证明了模型和算法的有效性，从而为大规模铁路救援的资源调度问题提供了有效的决策依据。

［1］张彦春，范艳萍，杨小礼.铁路突发事件应急物资优化调配［J］.铁道科学与工程学报，2011，8（6）：103-106.

ZHANG Yanchun，FAN Yanping，YANG Xiaoli.Optimization on Railway Emergency Materials Dispatching［J］.Journal of Railway Science and Engineering，2011，8（6）：103-106.

［2］周慧娟.铁路应急管理中的预案管理与资源配置优化［D］.北京：北京交通大学，2011.

［3］解兴申.铁路突发事件应急资源调配问题分析［J］.交通科技与经济，2010，12（2）：52-55.

XIE Xingshen.Study on the Scheduling Problem of Railway Emergency Materials［J］.Technology＆ Economy in Areas of Communications，2010，12（2）：52-55.

［4］FENG T，YAN R，TIAN Z.Optimization of Emergency Rescue Material Dispatching［C］／／ASCE.Reston：Iclem，2015：162-168.

［5］田志强，宋琦，潘金山，等.铁路突发事件应急救援设备调度优化研究［J］.铁道科学与工程学报，2015，12（1）：171-176.

TIAN Zhiqiang，SONG Qi，PAN Jinshan，et al.Optimization Analysis of Equipment Dispatching under Railway E-mergency Event［J］.Journal of Railway Science and Engineering，2015，12（1）：171-176.

［6］郑云水，穆然，林俊亭，等.铁路应急资源动态多阶段调度决策模型及算法研究［J］.计算机工程与应用，2015，51（20）：213-219.

ZHENG Yunshui，MU Ran，LIN Junting，et al.Research of Dynamic Multi-stage Scheduling Decision Model and Algorithm for Railway Emergency Resources［J］.Computer Engineering and Applications，2015，51（20）：213-219.

［7］ZHENG Y J，LING H F，SHI H H，et al.Emergency Railway Wagon Scheduling by Hybrid Biogeography-based Optimization［J］.Computers ＆ Operations Research，2014，43（1）：1-8.

［8］DUAN X，SONG S，ZHAO J.Emergency Vehicle Dispatching and Redistribution in Highway Network Based on Bilevel Programming［J］.Mathematical Problems in Engineering，2015，2015：1-12.

［9］CAO Y，LI Y，LI Z，et al.Discrimination Model of Priority of Seismic Emergency Rescue Zone［J］.Journal of Natural Disasters，2014，23（3）：181-189.

［10］郎坤，张明媛，袁永博.基于可变集的地震灾害应急物资分配模型［J］.灾害学，2014，29（1）：201-206.

LANG Kun，ZHANG Mingyuan，YUAN Yongbo.Allocation Model of Emergency Supplies in Earthquake Disasters Based on Variable Sets［J］.Journal of Catastrophology，2014，29（1）：201-206.

［11］李磊，孟学雷，韦强，等.基于案例推理的铁路行车事故应急决策方法研究［J］.铁道学报，2014，36（11）：1-6.

LI Lei，MENG Xuelei，WEI Qiang，et al.Research on E-mergency Decision Making for Railway Traffic Accidents Based on Case-based Reasoning［J］.Journal of the China Railway Society，2014，36（11）：1-6.

［12］舒其林.“情景-应对”模式下非常规突发事件应急资源配置调度研究［D］.合肥：中国科学技术大学，2012.

［13］周德群，张钦，陈超.基于优先权的多应急点资源调度模型研究［J］.经济问题，2011（7）：50-53.

ZHOU Dequn，ZHANG Qin，CHEN Chao.Research of Multi-emergency Depots Model for Resource Scheduling Based on Priority［J］.On Economic Problems，2011（7）：50-53.

［14］SHEU J B.Dynamic Relief-demand Management for E-mergency Logistics Operations under Large-scale Disasters［J］.Transportation Research Part E：Logistics ＆Transportation Review，2010，46（1）：1-17.

［15］王东海，段力伟.基于TOPSIS的铁路应急资源调度优化模型［J］.铁道运输与经济，2013，35（2）：52-56.

WANG Donghai，DUAN Liwei.Optimization Model of Railway Emergency Source Dispatching based on TOPSIS［J］.Railway Transport and Economy，2013，35（2）：52-56.

［16］尹辉.不确定情况下的危险品事故应急资源优化调度研究［D］.广州：华南理工大学，2013.

［17］王婧.不确定条件下应急物资多式联运调度模型研究［D］.武汉：华中科技大学，2013.

［18］常建鹏，陈振颂，周国华，等.基于前景理论的铁路应急预案多指标风险评估研究［J］.铁道学报，2016，38（2）：7-18.

CH ANG Jianpeng，CHEN Zhensong，ZHOU Guohua，et al.The Multi-index Risk Evaluation of Railway Emergency Plans Based on Prospect Theory［J］.Journal of the China Railway Society，2016，38（2）：7-18.

［19］BELMONT E，FRIED B M，GONEN J S，et al.Emergency Preparedness，Response＆Recovery Checklist Beyond the Emergency Management Plan［J］.Hospital Preparation for Bioterror，2006，16（37）：295-331.

［20］高学英.大规模应急救援资源布局与调度优化方法研究［D］.长春：吉林大学，2012.

［21］徐艳艳.应急物资调度模型及其求解方法［D］.长沙：中南大学，2011.

［22］杨洁，李登峰.求解梯形模糊矩阵对策的线性规划方法［J］.控制与决策，2015，30（7）：1219-1226.

YANG Jie，LI Dengfeng.Linear Programming Methodology for Solving Trapezoidal Fuzzy Matrix Games［J］.Control and Decision，2015，30（7）：1219-1226.