带角度控制的有限时间收敛导引律设计*
姚 奕,范作娥,冯林平
(海军潜艇学院,山东 青岛 266044)
0 引言
随着防空导弹以及防空雷达的不断发展,反舰导弹成功突防的难度越来越大,为了提高反舰导弹的突防概率,在突防敌方的防空导弹攻击水面舰艇时,希望反舰导弹能够从防空雷达的薄弱区进入,或者从防空火力弱的区域进入。为了获得最大的战斗部毁伤效果,对于特定的目标也希望战斗部以特定的命中角度侵入目标,而对于有较强防空能力的战斗群目标,则需要多枚反舰导弹分别从期望的攻击角度,同时对目标实施饱和攻击,以增加反舰导弹的突防能力[1]。这就使得反舰导弹在攻击敌方舰艇的时候,不仅仅希望导引头能够具有零脱靶量,实现精确打击目标,还要求导引头能够控制末端攻击目标的角度。要想实现反舰导弹末端攻击角度的控制,就需要设计带有角度控制的导引律。
为了设计合理有效的带角度控制的末端导引律,提高反舰导弹末端指定方向的突防能力,国内外许多学者针对这一问题进行了深入研究。有文献将比例导引进行改进,融合进其他控制理论,发展出增广比例导引用于末端角度控制,但是由于比例导引对于机动目标的鲁棒性有所欠缺,因此,实际应用过程中受到限制[2]。最优控制导引律具有自身很多优点,但是由于导弹控制过程中有太多不确定性因素,加之最优控制本身鲁棒性较差,容易对反舰导弹的打击精度造成不好影响。对于导弹制导系统来说,导弹在实际飞行过程中,不可避免地受到风的扰动、海浪扰动以及自身不确定性的影响,这就要求导弹的导引律具有强鲁棒性[3-4]。随着人们对变结构控制理论的深入研究,变结构控制对参数摄动和外部扰动的鲁棒性得到越来越多的重视,变结构控制理论在导弹制导系统里面的控制问题中得到了应用[5-6]。传统滑模变结构控制只能保证反舰导弹制导系统的状态,能够在有限时间内收敛至滑动模态,但在滑动模态上状态变量并不具有有限时间收敛的特性。因此,在导弹控制领域,制导系统状态的有限时间收敛问题开始受到越来越多的重视。文献[7]基于有限时间稳定性定理,设计了有限时间收敛导引律,但是不能进行角度控制。本文基于航向平面内导弹目标相对运动模型,根据非线性控制系统有限时间稳定性理论,研究了带角度控制的有限时间收敛导引规律。
1 导弹目标相对运动模型
在实际工程应用过程中,导弹与目标的运动关系是非线性的,为了研究问题方便,参考文献[8],将目标和导弹均视为质点,把导弹与目标的运动方程相对于理想弹道线性化。在上述条件下,垂直施加于导弹或者目标速度矢量的加速度矢量,仅仅改变导弹或者目标的速度方向,而不改变速度的大小。由于导弹和目标均视为质点,加之导弹的动态特性比制导回路的动态特性要快得多,因此,在导引律的设计过程中,忽略导弹控制系统的动态特性。
导弹与目标之间相对航向平面内运动关系见图1所示。参考导弹导引弹道的运动特性[8],定义导弹与目标的攻击坐标系xoy,选取基准线(或参考线)为。M为导弹,T为目标,连线即为目标瞄准线,又称为目标线或视线。

图1 导弹目标相对运动示意图
根据飞航导弹弹道学理论,导弹与目标的相对运动方程可以用定义在攻击平面内的极坐标参数r2、q2的变化规律来描述,相关参数的定义如下。
r2为导弹与目标之间的距离。r2=0表示导弹碰撞目标,即零脱靶量。
q2为目标瞄准线与基准线之间的夹角,称为目标瞄准角(又叫视线角)。从基准线逆时针旋转到瞄准线上,则定义视线角为正。
q˙2为视线角速率,即视线角相对于时间的变化率;
vm、vt分别定义为导弹与目标的运动速度。
φm、φt分别为导弹与目标的方位角。从基准线逆时针旋转到方位角上,则定义方位角为正。
由图1所示,根据极坐标参数r2、q2的变化规律,可得到如下的弹目相对运动模型。
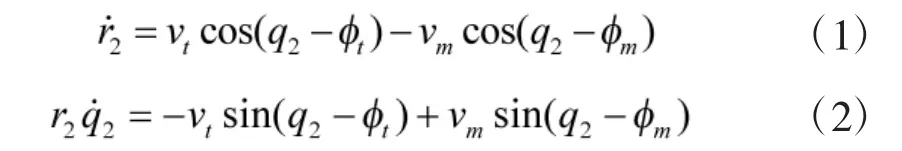

把式(5)~式(8)代入式(3)和式(4),并结合式(1)和式(2),经过整理得出:
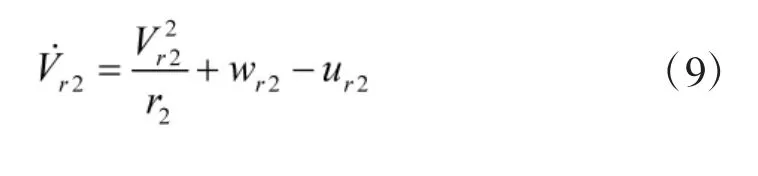
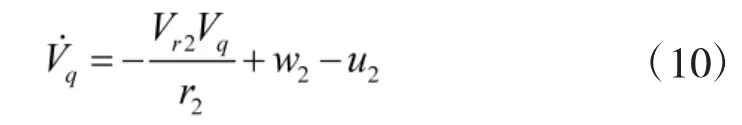
由式(5)和式(6)可以看出,wr2是目标加速度在视线方向上的分量,ur2是导弹加速度在视线方向上的分量。由式(7)和式(8)可以看出,w2是目标加速度在视线法向上的分量,u2是导弹加速度在视线法向上的分量。

导弹末端制导系统的导引律设计过程中,ur2只需在视线角稳定的前提下,导弹与目标的相对运动速度即可。在导弹实际攻击目标的过程中,导弹迎头拦截目标时,可以令ur2=0。因此,飞航导弹的末端导引律的设计问题,就转换为通过设计u2来控制视线角速率趋近于零,最好能够等于零,来最终实现导弹对目标的精确打击或者碰撞打击。
2 导引律设计
假设导弹末端雷达的开机初始时刻t=0,针对式(11)和式(12)的制导控制模型,此时制导控制系统的初始状态为;在t时刻,制导控制系统的状态为。定义系统的状态变量,其中为期望的导弹在打击目标时刻的视线角,定义系统的初始状态为,则制导控制系统模型可以转换为如下形式的时变微分方程:

式(13)就是经过适当的状态变换得到的新制导控制模型,在此制导模型里面,系统的状态变量既包含脱靶量因素,又包括终端落角约束,因此,如果能够设计合适的控制量,使得系统状态变量x能够在有限时间内收敛到平衡点,即,则就意味着导弹可以在精确打击目标的同时,同时能够控制末端攻击角度。
导弹末端雷达开机后,在制导系统导引导弹飞向目标的过程中,制导状态的下列不等式成立

在上述条件下,应用非线性有限时间收敛控制理论[9-10],可得出制导系统式(13)的状态变量有限时间收敛的充分条件,见如下定理。
定理1 对于制导系统(13),设计控制量u2使其满足式(15)成立:

其中,β2>0且为常数,则制导系统的状态变量x在有限时间内将收敛至零。
证明 选取光滑正定李雅普诺夫函数

则由式(15)可得:

由于导弹末制导飞行过程中不等式(14)成立,因此,有:

由定理1可知制导系统的状态变量x在有限时间tr1内收敛至零,收敛时间tr1满足

证毕。
根据定理 1,将式(13)代入式(15):

设计如下导引律:

将式(21)代入式(20)可得出:

由于不等式(22)成立,则根据定理 1,式(21)就是使导弹制导系统的状态在有限时间内收敛到零的导引律。而且由式(19)可以看出,β2越大,收敛时间tr1收敛速度越快,即视线角速率收敛至零q˙2→0的收敛速度越快,同时意味着视线角收敛到期望视线角q2→q2d的收敛速度越快。
导引律式(21)中可以看出,导引律中包含着目标加速度信息w2,由式(7)可以看出,w2是目标的加速度在视线法向上分量,导弹飞行过程中不能准确获得,但是可以通过近似估计来代替w2,假设一个足够大的正数ε2使得目标加速度的最大界限满足,那么在式(21)中用 ε2sgn(x2)代替 w2,得到导引律:
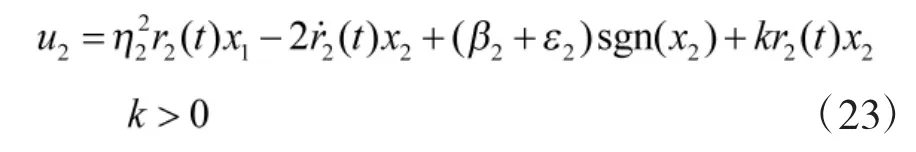
3 仿真研究
假设航向平面内导弹末端雷达开机时刻位置为(0,-5 600),敌方水面舰艇的位置为(10 000,0),单位均为m;反舰导弹速度为500 m/s,末端雷达开机时导弹弹道初始航向角0°。导弹打击目标时期望的末端航向角φd=-30°,选择导弹制导系统的有限时间收敛导引律参数:β2=380,ε2=20,η2=1,k=0.03。用饱和函数代替导引律中的开关函数,其参数选为δ=0.01(s-1)。

图2 弹道航向角φm

图3 导弹目标轨迹
上述仿真条件下,对本文设计的有限时间收敛导引律进行仿真验证,在制导系统攻击末端,导弹最终脱靶量0.3 m,末端实际落角-30.1°,相关仿真曲线见图2和图3。由上述仿真结果可以看出,本文设计的有限时间收敛导引律能够满足导弹精确打击目标的脱靶量要求,同时满足控制导弹末端攻击角度的要求,导引精度比较高。根据仿真曲线图2同时可以得出,导弹制导系统的收敛速度,受导引律系数β2的影响比较大,β2越大,制导系统的状态收敛速度越快,因此,通过选择不同的β2,可以控制制导系统的收敛速度。
4 结论
从工程实际出发,针对某型反舰导弹航向平面内的导弹与目标之间的相对运动模型,在不影响导弹打击精度前提下,考虑反舰导弹末端角度约束条件,应用有限时间稳定性理论,设计了带角度控制的有限时间收敛导引律,并可以通过导引律参数的选择来控制制导系统的收敛速度。由仿真结果可以看出,本文设计的导引律能够在满足高精度的前提下,实现角度控制,并且使制导状态在有限时间内收敛到稳定状态。
[1]唐江.智能反舰导弹协同攻击策略研究[J].飞航导弹,2011(11):57-61.
[2]张春妍.带角和时间约束的网络化导弹协同制导律[J].兵工学报,2016,37(3):431-438.
[3]LEE Y I,RYOO C K.Optimal guidance with constraints on impact angle and terminal acceleration [C]//AIAA Guidance,Navigation,and ControlConference and Exhibit,Austin,Texas,AIAA 2003-5795:1-7.
[4]JEON I S,LEE J I.Guidance law to control impact time and angle [C]//2005 International Conference on Control and Automation,Budapest,Hungary,WA1-4.1,2005:852-857.
[5]熊少华,王卫红,王森.带攻击角度约束的非奇异快速终端滑模制导律 [J].控制理论与应用,2014,31(3):268-278.
[6]LEVANT A.Principles of 2-sliding mode design[J].Aotomatica,2007(43):576-586.
[7]孙胜,周荻.有限时间收敛变结构导引律[J].宇航学报,2008,29(4):1258-1262.
[8]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000:53-57.
[9]洪奕光,程代展.非线性系统的分析与控制[M].北京,科学出版社,2005:225-228.
[10]HONG Y G.Finite time stabilization and stabilizability of a class of controllable systems[J].Systems&Control Letters,2002,46(2):231-236.

