高炮武器射击精度试验技术研究
姚兴太,史海龙,宋春燕,杨宁国
(中国白城兵器试验中心,吉林 白城 137001)
0 引言
射击精度是高炮武器重要的战术技术指标,对其进行考核是设计定型试验的一项重要内容。目前靶场进行高炮射击精度考核都是通过实弹射击实现的,即在试验过程中取得每一次射击后的弹着点偏差数据,然后根据现有军标中规定的方法进行计算。当数据间不是完全独立时,若仍采用传统的计算方法,则结论的科学性将会降低,本文通过建立误差序列时空特性理论,从确定相关系数入手,可解决上述问题,从而丰富和完善现有试验理论。
1 误差序列时空特性理论
1.1 误差序列时空特性定义
在假定误差序列为平稳随机序列的条件下,可按以下公式定义误差的3个特征指标:均值、均方差σz与相关系数rz。

1.2 误差序列时空特性估计



式中,n-1为分布的自由度。
1.3 相关系数确定
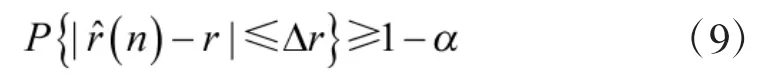

t服从自由度为n-2的student分布,此时

以概率1-α成立。如果上式被满足,r=0即可依式(11)给出的置信区间与显著水平而被接受。
将n-2=50代入式(11),可得相关系数的置信区间为(0,0.2025)。由于=0.145 1在其置信区间内,故可以判定其相关系数为0,脱靶量序列不相关。
表1 相关系数=0.145 1的脱靶量序列

表1 相关系数=0.145 1的脱靶量序列
n 123456789 z -305.1 95.3-242.7 n 10 1112-204.8 816.3 -77 1317 18-200.4 14 4.3 447.8 15 16-373.1 114.6 -245.2 n z -123.9 -142.4 260.3 -49.8 192 287 19 20 21 22 23 24 25 26 27 z -363 132.5 23.4 578 413.8 259.2 78.5 -159.7 87.9 n 28 29 30 31 32 33 34 35 36 z -8.3 435.9 162.4 -201.5 158.5 3.4 215.3 29 -6.5 n 37 38 39 40 41 42 43 44 45 z -215.7 68.7 -10.9 284.5 -200.2 27.5 124.1 43.8 -417.6 n 46 47 48 49 50 51 52 z -562.4 -437.3480.1-155.3395.3185.5 204.8
2 高炮武器射击精度试验技术
对高炮武器而言,其射击诸元误差、脱靶量误差,虽说都被假定为平稳正态序列,但由于其间存在相关性,因而无法套用student、2等分布来讨论在有限次测量下其均值与方差的置信区间与置信概率,给定型试验方案的制定带来明显的困难。
利用前面建立的误差序列时空分布理论则可以解决这一问题。即:如果弱相关误差满足方程



3 高炮射击精度检测方案
3.1 决定相关系数
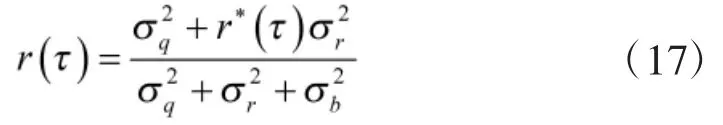
此时,上述3种误差合成为已知参数的弱相关误差;如果上述数据不存在,则按2.3节给出的理论计算即,式中,为射击间隔。
3.2 构建均值——方差等效的不相关序列

3.3 检测系统误差

由于各个航次要求是相互独立的,故有
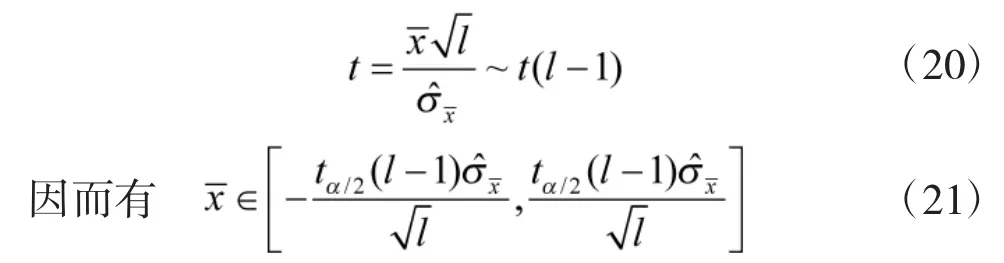
的置信概率为
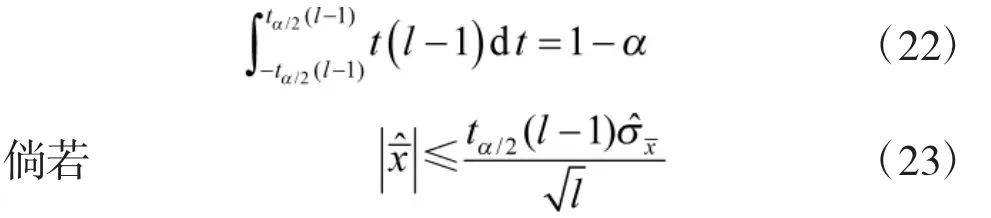
则认定射击误差取自均值为零的无限序列,此时,其计算值虽不为零,但应认为是采样数量不足所致。否则,认定均值

3.4 检测均方差
当l→∞时,

式中,σ0为射击误差均方差的战技指标,Kσ为小样本修正系数,按表2进行。若上式得到满足,则指标可接受;否则拒绝。

表2 均方差小样本测量修正系数表
4 结论
本文利用误差序列时空分布理论,推导出了基于射击误差时空特征量的射击精度评定模型,给出了高炮射击精度的检测技术,为科学考核高炮武器射击精度提供了方法。本文给出的试验技术同样也适用于对雷达、光电等的探测精度及导航与姿态测量系统的寻北精度、动态测量精度等指标的考核。
[1]潘承泮.武器系统射击效力[M].北京:兵器工业出版社,1994.
[2]田棣华,肖元星,王向威,等.高射武器系统效能分析[M].北京:国防工业出版社,1991.
[3]郭治.现代火控理论[M].北京:国防工业出版社,1996.

