基于容积变换的平滑变结构滤波及应用

林孝工, 焦玉召, 李 恒, 梁 坤, 聂 君

(哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)

0 引 言

随着对海洋资源的探索,船舶动力定位技术也得到了更多关注[1-2]。对可微非线性系统,将非线性系统模型展开为关于均值的泰勒多项式,仅保留线性部分,即得扩展卡尔曼滤波(extended Kalman filter,EKF)[3]算法。EKF需计算Jacoby矩阵,且有高阶截断误差。因而对强非线性系统,可能会出现估计误差较大或者无法收敛的情况。此时可计算Jacoby和Hessian矩阵得到二阶扩展卡尔曼滤波(second-order extended Kalman filter,SOEKF)[4],但计算量大。非线性滤波的另一种策略是基于Sigma点的无迹卡尔曼滤波(unscented Kalman filter,UKF)[5],UKF不需要Jacoby矩阵。同时基于球面径向容积规则,得到容积卡尔曼滤波(cubature Kalman filter,CKF)[6]。且这些非线性状态估计方法,已广泛应用于惯性导航[7]、状态估计[8]等。同时通过平方根因子传递,可保证算法的数值稳定性[9-10]。

模型精确时,基于Kalman的滤波器具有较高估计精度,然而模型参数不确定或噪声干扰的随机性,传统算法可能会发散[11]。故文献[12]将滑模概念引入滤波增益的计算中,提出变结构滤波(variable structure filter,VSF)。VSF是一种基于不确定模型的滤波算法,通过引入平滑边界层,得到具有固定平滑边界层的平滑变结构滤波[13]。实际系统干扰和不确定性具有随机性,令估计误差协方差对平滑边界层求偏导,可得近似最优平滑边界层[14]。文献[15]将边界层扩展为全矩阵形式,得到具有最优平滑边界层的平滑变结构滤波(smoothing variable structure filter,SVSF)算法。

模型不确定时,SVSF是一种有效的滤波算法[16-17]。但仍具有一定局限性:①要求系统方程是适度非线性且可微,需计算系统的Jacoby矩阵;②受计算机字长限制,误差积累可能使协方差失去非负定性,导致滤波发散。为解决这两个问题,一方面将CKF与具有最优平滑边界层的SVSF算法相结合,利用容积规则计算状态预测值、状态协方差预测、测量预测值和测量协方差预测值,得到了基于容积规则的平滑变结构滤波(cubature-smoothing variable structure filter,C-SVSF)算法,既提高了SVSF算法的估计精度,又扩展了SVSF算法的应用范围。另一方面,通过在状态传递过程中使用协方差的平方根因子,保证协方差的正定性和对称性,得到平方根容积平滑变结构滤波(square root cubature-smoothing variable structure filter,SRC-SVSF),SRC-SVSF是具有数值稳定性的滤波算法。

1 基于Jacoby的SVSF

考虑非线性系统:

xk=fk-1(xk-1)+ωk

(1)

zk=hk(xk)+υk

(2)

式中,fk-1(·)和hk(·)表示状态方程和测量方程;xk是状态矢量;zk是观测值;ωk和υk是状态噪声和观测噪声,服从高斯分布ωk～N(q,Q),υk～N(r,R),其中q和r是均值,Q和R是方差。

假设1假设系统式(1)和式(2)满足文献[13]中的定义,即不考虑测量噪声时,系统xk=fk-1(xk-1)和zk=hk(xk)是连续的双射或是完全可观和完全可控的,即通过观测矢量zk存在一个逆映射能唯一的得到状态矢量xk,即

(3)

如果系统式(1)、式(2)转换矩阵fk和hk是常系数,那么直接得卡尔曼滤波器。如果转换矩阵是非线性的,那么可通过计算Jacoby矩阵得EKF算法。

对模型不精确系统,EKF误差较大,而SVSF可有效抑制模型不精确带来的滤波发散。原理如图1所示,当预测值超出存在的子空间时,说明有不确定干扰,可通过不连续增益将估计值矫正到真实值附近,保证算法对不确定干扰的鲁棒性。

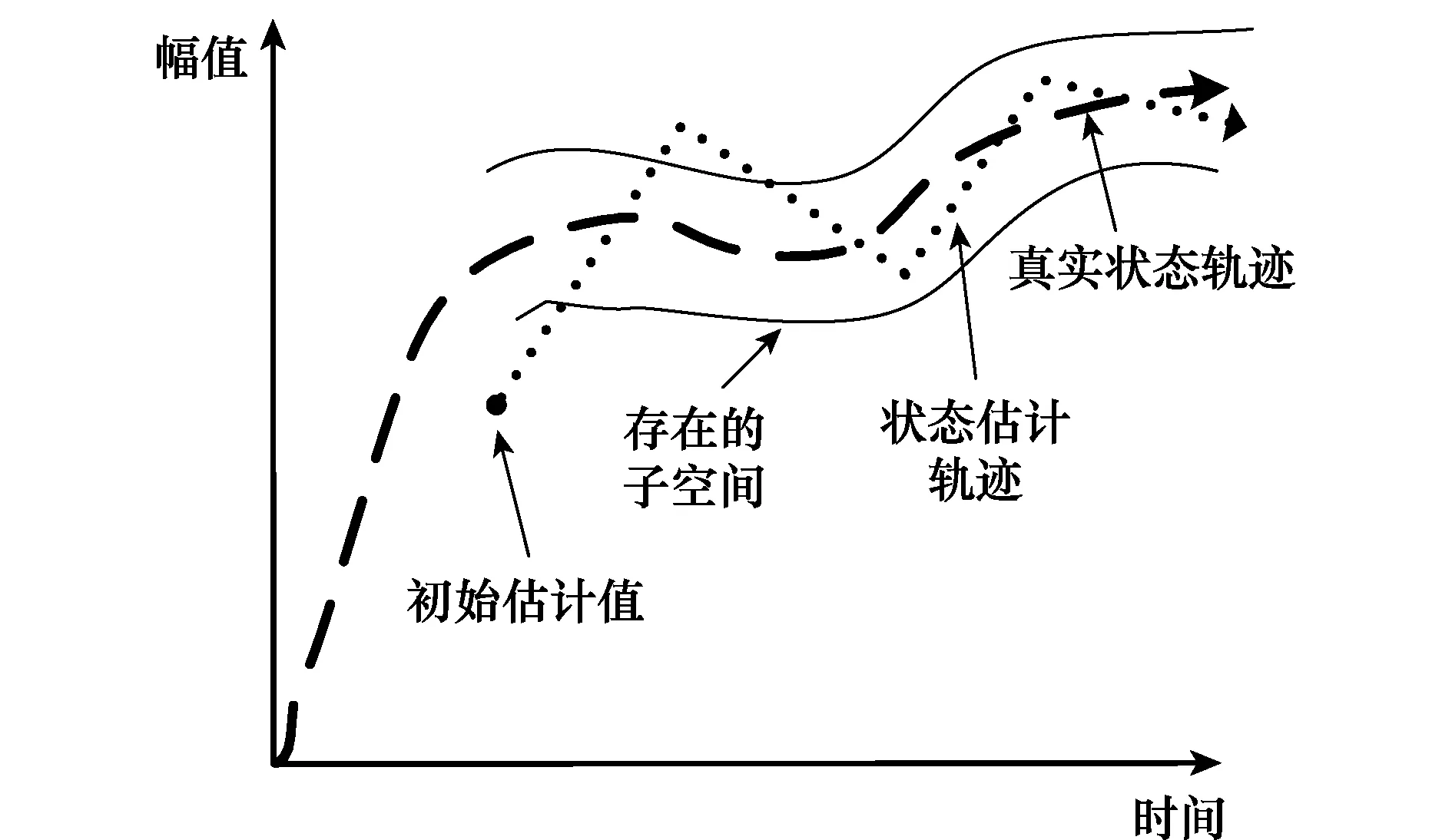
图1 SVSF算法概念图Fig.1 Concept of SVSF

同时,为消除不连续增益的频繁切换造成的系统颤动,文献[13]引入固定平滑边界层。假设系统存在有界随机干扰,那么令平滑边界层等于该干扰的保守上界。通过引入饱和函数式(4),当估计误差大于边界层时,用不连续增益来保证算法稳定运行;当误差在边界层内时,用连续增益进行状态估计,进而消除一定的颤动影响。

(4)

图2 具有边界层的SVSFFig.2 SVSF with smooth boundary layer

实际中该上界不容易获得,文献[14-15]提出具有协方差导引的平滑变结构滤波算法。基于状态估计误差协方差最小原则得到具有最优平滑边界层的SVSF。状态预测值和测量估计值分别为

(5)

(6)

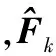
(7)

状态预测误差协方差为

(8)

测量预测值为

(9)

新息ez,k+1|k和测量估计误差ez,k+1|k+1为

(10)

(11)

基于新息和测量误差,得增益[15]为

⊗

(12)

进而,可得状态估计更新值为

(13)

估计误差协方差更新值为

(14)

(15)

式(5)～式(14)即是变结构滤波算法。下面通过引理1进一步证明算法的稳定性问题。

引理1若估计误差满足式(16),则状态估计过程是稳定和收敛的[13]。

|ek|<|ek-1|

(16)

因而,只需证明状态估计误差满足引理1,就可证明出状态估计过程是稳定和收敛的。

定理1若系统满足假设1,状态增益满足不等式,那么滤波算法是稳定和收敛的。

|ez,k+1|k|<|Hk+1Kk+1ez,k+1|k|<|ez,k+1|k|+|ez,k|k|

(17)

sign(Hk+1Kk+1ez,k+1|k)=sign(ez,k+1|k)

(18)

证明由不等式(17)可知,|Hk+1Kk+1ez,k+1|k|-|ez,k+1|k|<|ez,k|k|成立,又由于Hk+1Kk+1ez,k+1|k与ez,k+1|k同号,那么可得,|ez,k+1|k-Hk+1Kk+1ez,k+1|k|<|ez,k|k|。结合式(6)和式(9)～式(13),得ez,k+1|k-Hk+1Kk+1ez,k+1|k=ez,k+1|k+1。则不等式|ez,k+1|k+1|<|ez,k|k|成立。又由于系统是完全可观和可控的,因而知|ex,k+1|k+1|<|ex,k|k|成立,满足引理1,故估计算法是稳定和收敛的。

证毕

由上可知,对于完全可观和完全可控的系统,状态估计误差具有稳定性和收敛性的充分条件是输出估计误差是稳定和收敛的。因而,由定理1,令增益为

(19)

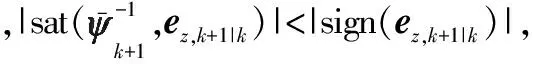
综上,SVSF对不确定非线性系统具有一定的鲁棒性,但是仍无法克服EKF算法的局限性。针对此,一种直接的思路是通过容积变换来代替非线性系统的线性化,得到CKF算法。CKF由于不需要计算Jacoby矩阵,同时简化了计算,因而得到了广泛的应用。

2 基于容积变换的非线性滤波策略

2.1 CKF算法

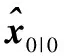
(20)

状态预测值和协方差预测值为

(21)

(22)

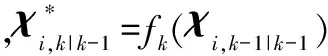
测量预测值和新息协方差为

(23)

(24)

估计误差互协方差为

(25)

以上即是CKF的状态和协方差预测方程。

2.2 C-SVSF算法

基于以上描述,CKF预测方程可有效克服EKF的缺点。因而本文考虑采用容积规则来计算SVSF的状态预测和协方差预测值,从而得到C-SVSF算法。C-SVSF不仅保持了SVSF算法的鲁棒性,而且不需要计算系统的Jacoby矩阵,因而估计精度将高于SVSF算法。C-SVSF算法流程如下。

步骤1状态预测式(5)和协方差预测式(8)分别变为式(21)和式(22)。从而得到基于容积规则的状态预测和协方差预测值。

步骤2上一时刻的测量估计误差ez,k-1|k-1

首先，计算观测方程的传递容积点为

(26)

(27)

则测量估计误差为

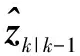
(28)

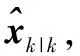
以上即是C-SVSF算法,克服了非线性系统式(1)必须连续可微的条件,且不需要计算系统的Jacoby矩阵,即保持了SVSF的鲁棒性,又由于容积规则的引入使得状态预测和协方差预测的精度得到了进一步提高。因而得到的C-SVSF算法估计精度理论上要高于基于Jacoby矩阵的扩展平滑变结构滤波(extended-SVSF,E-SVSF)算法。同时与标准E-SVSF算法具有相同的滤波框架,因而仍是一种稳定的滤波算法。

与CKF相似,C-SVSF在最优边界层计算中要求计算协方差的逆矩阵,因而协方差矩阵需要满足非负定性的要求。然而由于计算机字长限制或者误差的累计可能会使协方差失去非负定性,从而导致算法数值发散。因而,为了提高C-SVSF算法的数值稳定性,类似于平方根容积卡尔曼滤波算法[6],由下三角分解的方法给出了SRC-SVSF算法。

2.3 SRC-SVSF算法

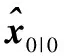
(29)

式中

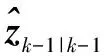
步骤3新息协方差平方根因子为

(30)

步骤5估计误差协方差平方根因子更新公式为

(31)

综上,将容积卡尔曼滤波策略中计算状态和协方差预测的方法引入到SVSF算法中,得到的C-SVSF由于不需要计算非线性系统式的Jacoby矩阵,因而其估计精度要高于E-SVSF算法,且SRC-SVSF保障了算法的数值稳定性。

3 仿真实验及分析

建立三自由度船舶运动方程[2]为

(32)

三自由度观测方程为

zk+1=hk(xk)+υk

(33)

对非线性动力定位船舶位置估计系统,CKF算法的估计精度要高于EKF算法的估计精度。因而以CKF作为对比算法，分别在观测噪声协方差已知和未知两种情况下,与E-SVSF、C-SVSF和SRC-SVSF算法进行仿真对比。

3.1 观测噪声协方差精确已知

假设测量噪声协方差是精确已知的,即R=diag([20,20,20,20,20,20])。采样周期1 s,采样时间1 800 s。通过200次蒙特卡罗仿真实验,4种算法下船舶位置和速度RMSE分别如图3和图4所示。

图3 已知噪声下的北-东-艏向位置RMSEFig.3 RMSE of north-east-head with known noise

图4 已知噪声下的纵荡-横荡-艏摇RMSEFig.4 RMSE of surge-sway-yaw with known noise

由于在噪声已知时,CKF是最优状态估计算法,故CKF具有最小RMSE。由于状态和协方差预测引入了Jacoby矩阵,因而E-SVSF误差最大。同时,容积规则的引入使C-SVSF算法精度高于E-SVSF。而SRC-SVSF算法由于状态传递过程中使用协方差的平方根因子,因而与C-SVSF具有几乎相同的估计误差。表1是状态在不同算法下的平均RMSE。可知C-SVSF及其平方根形式SRC-SVSF具有相同估计误差,且都高于E-SVSF,说明了改进算法的有效性。

表1 已知噪声下算法的平均RMSE

3.2 观测噪声协方差未知

假设测量噪声协方差未知,即可令R=diag([500,500,1 000,1 000,1 000,1 000])。采样周期仍为1 s,采样时间1 800 s。通过200次蒙特卡罗仿真实验,可得此时船舶位置和速度RMSE分别如图5和图6所示。可知当测量噪声协方差未知时,由于CKF算法不具有鲁棒性,因而CKF估计误差最大。而基于SVSF的滤波算法对不确定干扰具有一定的鲁棒性,因而估计精度高于CKF算法。同时由于容积规则的引入,C-SVSF和SRC-SVSF算法的估计精度要高于E-SVSF算法,这与理论分析相一致。同时，表2给出了测量噪声协方差未知时,4种算法下的平均RMSE。

图5 未知噪声下的北-东-艏向RMSEFig.5 RMSE of north-east-head with unknown noise

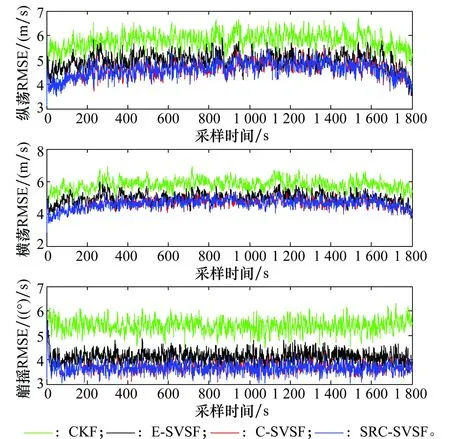
图6 未知噪声下的纵荡-横荡-艏摇RMSEFig.6 RMSE of surge-sway-yaw with unknown noise

算法参数x′/my′/m/(°)u/(m/s)v/(m/s)r/((°)/s)CKF6．676．668．325．785．785．39E⁃SVSF4．224．227．044．954．954．12C⁃SVSF4．124．123．894．594．613．65SRC⁃SVSF4．124．123．894．594．613．65

综上可知:测量噪声协方差已知时,C-SVSF、SRC-SVSF与CKF具有相近估计精度,且都高于E-SVSF的估计精度;当测量噪声协方差未知时,C-SVSF、SRC-SVSF具有相似估计精度,且高于E-SVSF,同时由于SVSF对噪声干扰的鲁棒性,因而精度均高于CKF。进一步说明本文C-SVSF和SRC-SVSF算法的有效性以及存在噪声干扰时算法的鲁棒性。

4 结 论

本文提出了C-SVSF算法,该算法既能消除Jacoby矩阵计算,又能充分利用SVSF的鲁棒性;为保证算法的数值稳定性,给出SRC-SVSF算法。由仿真知,当测量噪声协方差已知,C-SVSF、SRC-SVSF与CKF具有相似估计精度且高于E-SVSF;当测量噪声协方差未知,C-SVSF、SRC-SVSF估计精度仍高于E-SVSF,同时由于SVSF的鲁棒性,基于SVSF的估计精度均高于CKF,进一步说明所提算法的优越性。因而,C-SVSF和SRC-SVSF可以作为船舶状态估计器使用,且当测量噪声协方差未知时,可以替代已有的E-SVSF或CKF进行状态估计。

[1] 边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京:科学出版社, 2011.

BIAN X Q, FU M Y, WANG Y H. Ship dynamic positioning[M]. Beijing: Science Publishing Company, 2011.

[2] 徐树生. 船舶动力定位系统多传感器信息融合方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.

XU S S. Research on the multi-sensor information fusion methods of vessel dynamic positioning system[D]. Harbin: Harbin Engineering University, 2013.

[3] HAUG A J. Bayesian estimation and tracking: a practical guide[M]. New Jersey: Wiley, 2012.

[4] MAHALANABIS A K, FAROOQ M. A second-order method for state estimation of non-linear dynamical systems[J]. International Journal of Control, 1971, 14(4):631-639.

[5] QUINE B, UHLMANN J, DURRANTWHYTE H. Implicit Jacobians for linearised state estimation in nonlinear systems[C]∥Proc.of the American Control Conference, 1995:1645-1646.

[6] ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Trans.on Automatic Control, 2009, 54(6):1254-1269.

[7] LIU M, LAI J, LI Z, et al. An adaptive cubature Kalman filter algorithm for inertial and land-based navigation system[J]. Aerospace Science & Technology, 2016, 51(2):52-60.

[8] LIN C, GONG X, XIONG R, et al. A novelH∞, and EKF joint estimation method for determining the center of gravity position of electric vehicles[J].Applied Energy,2017,194:609-616.

[9] 徐树生, 林孝工, 赵大威. 强跟踪SRCKF及其在船舶动力定位中的应用[J]. 仪器仪表学报, 2013, 34(6):1266-1272.

XU S S, LIN X G, ZHAO D W. Strong tracking SRCKF and its application in vessel dynamic positioning[J]. Chinese Journal of Scientific Instrument, 2013, 34(6): 1266-1272.

[10] 付梦印. Kalman滤波理论及其在导航系统中的应用[M]. 北京:科学出版社, 2010.

FU M Y. Kalman filtering theory and its application in navigation system[M]. Beijing: Science Publishing Company, 2010.

[11] TIAN T, SUN S, LI N. Multi-sensor information fusion estimators for stochastic uncertain systems with correlated noises[J]. Information Fusion, 2016, 27(C):126-137.

[12] HABIBI S R, BURTON R, HABIBI S R, et al. The variable structure filter[J]. Journal of Dynamic Systems Measurement & Control, 2002, 125(3):157-165.

[13] HABIBI S. The smooth variable structure filter[J]. Proceedings of the IEEE, 2007, 95(5):1026-1059.

[14] GADSDEN S A, EL SAYED M, HABIBI S R. Derivation of an optimal boundary layer width for the smooth variable structure filter[C]∥Proc.of the American Control Conference, 2011:4922-4927.

[15] GADSDEN S A, HABIBI S R. A new robust filtering strategy for linear systems[J]. Journal of Dynamic Systems Measurement & Control, 2012, 135(1):359-370.

[16] ATTARI M, GADSDEN S A, HABIBI S. Target tracking formulation of the SVSF with data association techniques[J]. IEEE Trans.on Aerospace & Electronic Systems, 2017, 53(1):12-25.

[17] ATTARI M, LUO Z, HABIBI S. An SVSF-based generalized robust strategy for target tracking in clutter[J]. IEEE Trans.on Intelligent Transportation Systems, 2016, 17(5):1381-1392.