基于星联合分布的星图识别

姜 笛, 张 科, DEBEIR Olivier

(1. 西北工业大学航天学院, 陕西 西安 710072; 2. 法语布鲁塞尔自由大学图像、信号处理及声学实验室,比利时 布鲁塞尔 1050; 3. 西北工业大学航天飞行动力学国家级重点实验室, 陕西 西安 710072)

0 引 言

应用于卫星等空间飞行器的星敏感器技术的出现为空间飞行器的姿态测量开辟了新途径,其利用恒星坐标系作为参照坐标系,由于恒星在参照坐标系中的空间位置可以认为是固定不变的,且星光矢量具有很高的测量精度,因此星敏感器可以达到相比于地球敏感器、太阳敏感器、全球卫星定位系统和磁力计等更高的测量精度[1-5]。星图识别是星敏感器准确确定飞行器的空间姿态的重要前提。目前发展到第3代的星载星敏感器,具有高分辨率成像元件,具备全天星图识别功能。对于全天星图识别,子图同构类星图识别直接或间接利用角距,在全天星图中寻找唯一符合匹配条件的子图[6]。模式识别类星图识别在星表中寻找与观测星模式最相近的导航星,较子图同构算法能更好地减少冗余,准确性更高。其中以栅格算法为代表[7],先确定主星及模式半径、定位星,以主星和定位星连线为坐标轴对视场进行旋转,最后将视场划分为栅格,以0、1表示栅格中是否含有观测星,构造星模式。

在栅格算法基础上,产生了很多改进的全天星图识别算法,如文献[8]用损失函数量化栅格中星的位置及亮度变化,文献[9]在二维栅格基础上添加了第三维—星等亮度构建三维栅格,文献[10]用构建了扩展的环形栅格,文献[11]在极坐标系中重新构建栅格, 文献[12]对在星图中构建的环带进行编码,引入查找表,使得匹配查找的速度得以提升,文献[13]将各邻近星与主星的距离进行排序,构建检索树。

无论是原有或改进的栅格类算法,缺点在于正确选择定位星的概率不高。在定位星确定错误时,将产生错误的特征模式,这样获得正确识别的可能性几乎为零。并且,栅格尺寸的选择合适与否在很大程度上影响特征模式的构成,从而影响匹配的准确性,例如,由于星点测量误差,位于栅格边缘的星可能由一个栅格移向其他栅格,因此相似的分布特征可能提取出差别较大的模式向量。另外,在星点分布密集的位置,可能由于栅格尺寸选择不当的原因,出现多个星点位于同一栅格的现象。

提出了一种适用于第3代星载星敏感器高分辨率成像元件的全天星图识别方法。根据星图中的星联合分布特征,将星图划分为与每颗星唯一对应的多边形,提取多边形的结构特征,这样得到的特征不受视场旋转的影响,提取过程也不需要对视场进行平移,可缩短生成特征模式所需要的时间,同时不需要确定定位星及选择栅格尺寸,能有效提升匹配的准确性。

1 基于星联合分布的识别方法

这里以视场大小为12°×12°,像素分辨率为512×512的星敏感器为例进行说明。

1.1 星图特征提取

将待识别星图中的所有相邻星连接形成多个三角形,对每个三角形作三条边的垂直平分线,将这些垂直平分线的交点连接,可以得到与每颗星对应的多边形,如图1所示。可以看出,生成的每个多边形中仅含有一颗星,并且每颗星均位于一个多边形中。

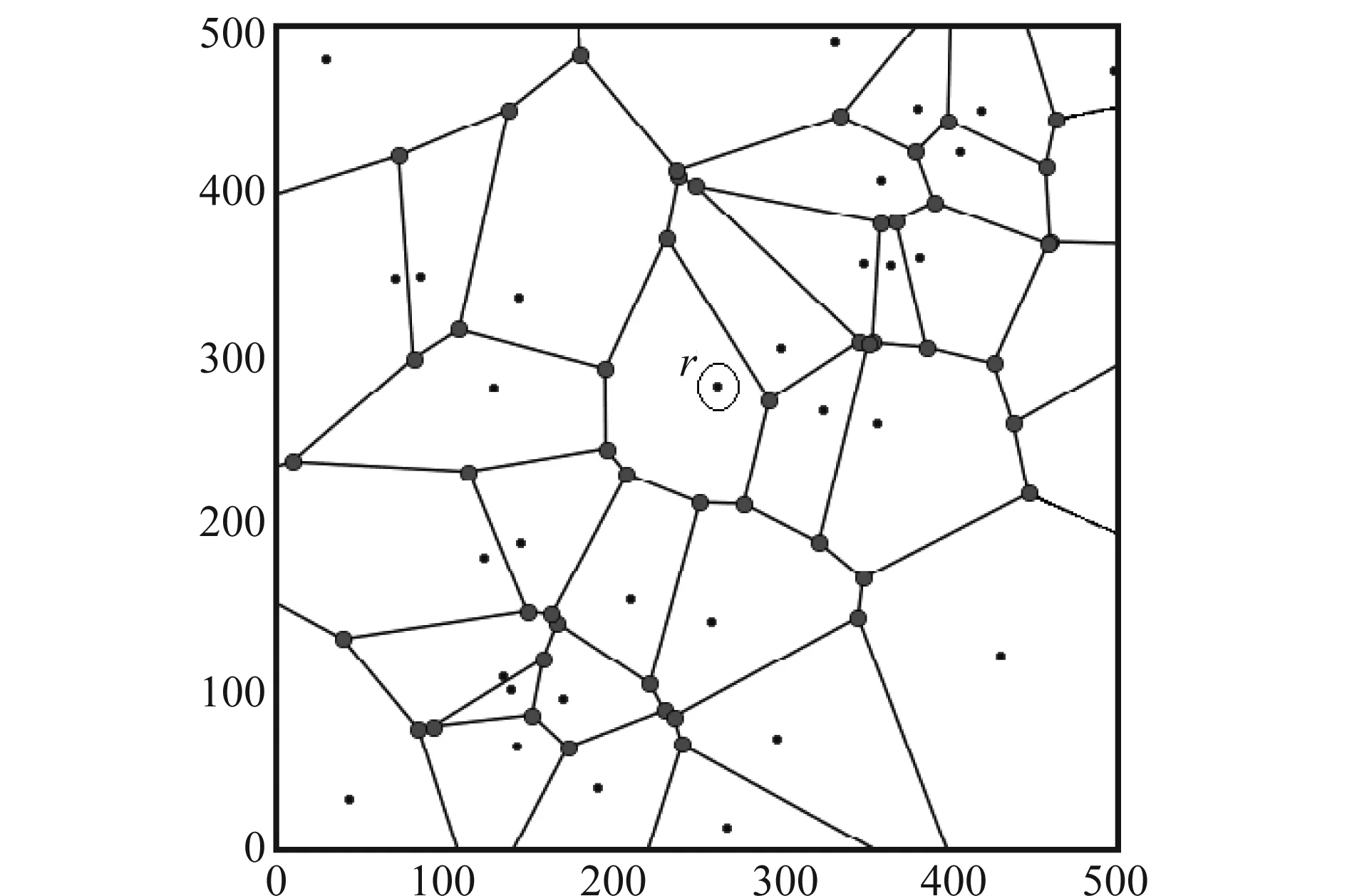
图1 将待识别星图划分为多边形Fig.1 Dividing the star image to be identified into polygons

根据欧拉拓扑定理,简单多面体的顶点数v、面数f及棱数e间有

v+f-e=2

如果多面体退化为一个无限远处的顶点p∞与不包含这一顶点的所有面组成的平面图形,得到如图2所示的多边形的集合。

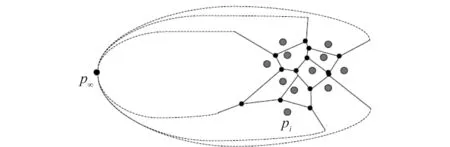
图2 多面体退化为多边形的集合Fig.2 Polyhedron degenerating into aggregate of polyons

对含有n颗星的待识别星图,将其划分为n个多边形的集合,每个多边形包含一颗星pi,有f=n,那么

v+1-e+n=2

(1)

(2)

vi≥3

(3)

由式(1)～式(3)得

v≤2n-5

e≤3n-6

在存在位置噪声的情况下,即使星点在图中发生位移,由于星图的划分是在所有图中星点联合分布的基础上进行的,因此对得到的多边形结构的影响将大幅下降。

以图1中最接近图像中心的星r为主星,对包含主星的多边形,将其最大内角αn、最小内角α1、边数n、最长边ln、最短边l1作为特征,构成待识别星图的特征模式向量{αn,α1,n,lk,l1}。

1.2 构建导航数据库

将耶鲁亮星星表(bright star catalgue,BSC)中星等低于6.5等的9 110颗星去掉变星及双星,得到9 082颗星作为导航星库。将导航星库中每颗星在天球坐标系中的矢量分别作为星敏感器的视轴指向,生成以这颗星为主星的星图。同样将这些星图划分为包围图中每颗星的多边形的集合,同理,可以根据主星对应的多边形构造导航星的特征模式向量{αknk,αk1,nk,lknk,lk1},其中,k为主星在导航星库中的序号。

1.3 匹配识别

对导航星库中各星的特征模式向量和观测星图进行比对,如果导航星Sk满足

(4)

则认为匹配成功,如果有多于一颗的导航星满足式(4),认为模式向量与{αn,α1,n,lk,l1}相差最小的导航星与r相匹配。

对于图1中的主星r,假设通过以上步骤得到与其匹配的导航星S,将星敏感器视轴对准这颗星的方位,可以生成以这颗导航星为中心的星图,如图3所示。

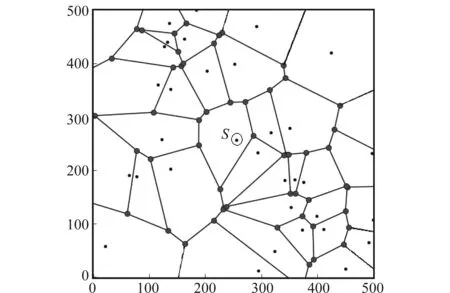
图3 仿真生成星S的邻域Fig.3 Neighbourhood of star S generated thrugh simulation

将图3进行旋转、平移,其中的星将与待识别的星图图1中的星重合,由此可以验证匹配的正确性。

2 仿真试验

通过仿真试验验证识别方法针对星图噪声的鲁棒性,是对识别方法性能进行评价的主要途径[14]。为了对识别方法的效果进行分析,在全天范围内随机生成星图,在1.6 GHz Pentium (R)计算机及Matlab环境中进行全自主识别的试验。

2.1 位置噪声存在时的性能

定义位置噪声概率,这一概率实际上是一个比例,表示星图中的全部星体中占这一比例的星将以相同概率1/8向与其相邻的8个像素之一移动。当位置噪声概率为0时,星图中每颗星都在原有位置,当位置噪声概率为1时,星图中每颗星都移向其相邻的8个像素之一[8]。在向星图中加入的位置噪声概率由0至0.7变化的情况下,在生成的随机指向的1 000幅星图中,用栅格算法和提出的算法分别进行星体的识别,识别的正确率结果如图4和表1所示。

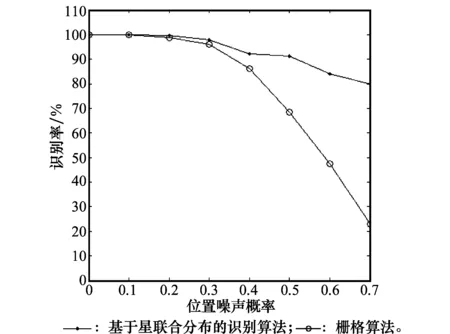
图4 加入位置噪声的情况下,栅格算法和基于星体联合分布的识别算法的识别率变化 Fig.4 Change of recognition rates of grid algorithm and recogntion based on mutual star distribution with position noise is added

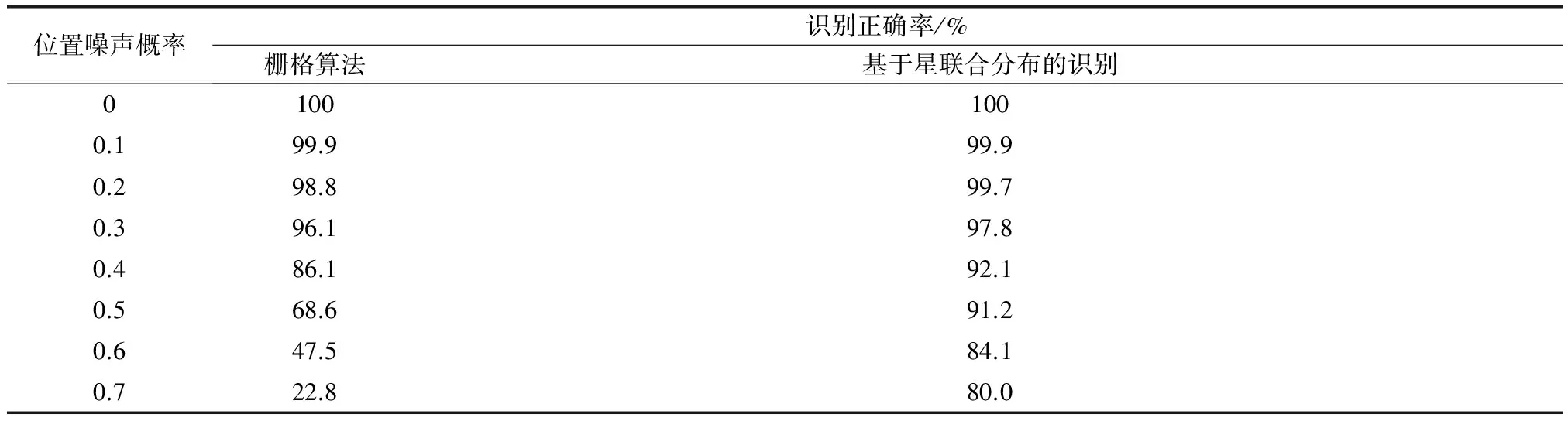
位置噪声概率识别正确率/%栅格算法基于星联合分布的识别01001000．199．999．90．298．899．70．396．197．80．486．192．10．568．691．20．647．584．10．722．880．0

从图4及表1中可以看到,栅格算法的识别率大幅下降,其特征模式受到位置变化影响严重,基于星联合分布的识别方法解决了这一问题。当位置噪声概率增加至0.5时,基于星联合分布的识别方法仍然能表现出90%以上的识别正确识别率。因此,在仅有位置噪声存在的情况下,基于星联合分布的识别方法比栅格算法具有更加稳定的性能和更强的鲁棒性。

2.2 位置噪声及亮度噪声存在时的性能

位置噪声和亮度噪声在星图中是同时存在的。如果亮度噪声使得星图中星的视星等高于7等,那么这颗星将不能被观测装置捕获,在星图中将不能显示[8]。在星图中加入高斯亮度噪声,当位置噪声保持概率0.4不变,亮度噪声标准差由0增加到2.5时,星图的识别正确率如图5和表2所示。

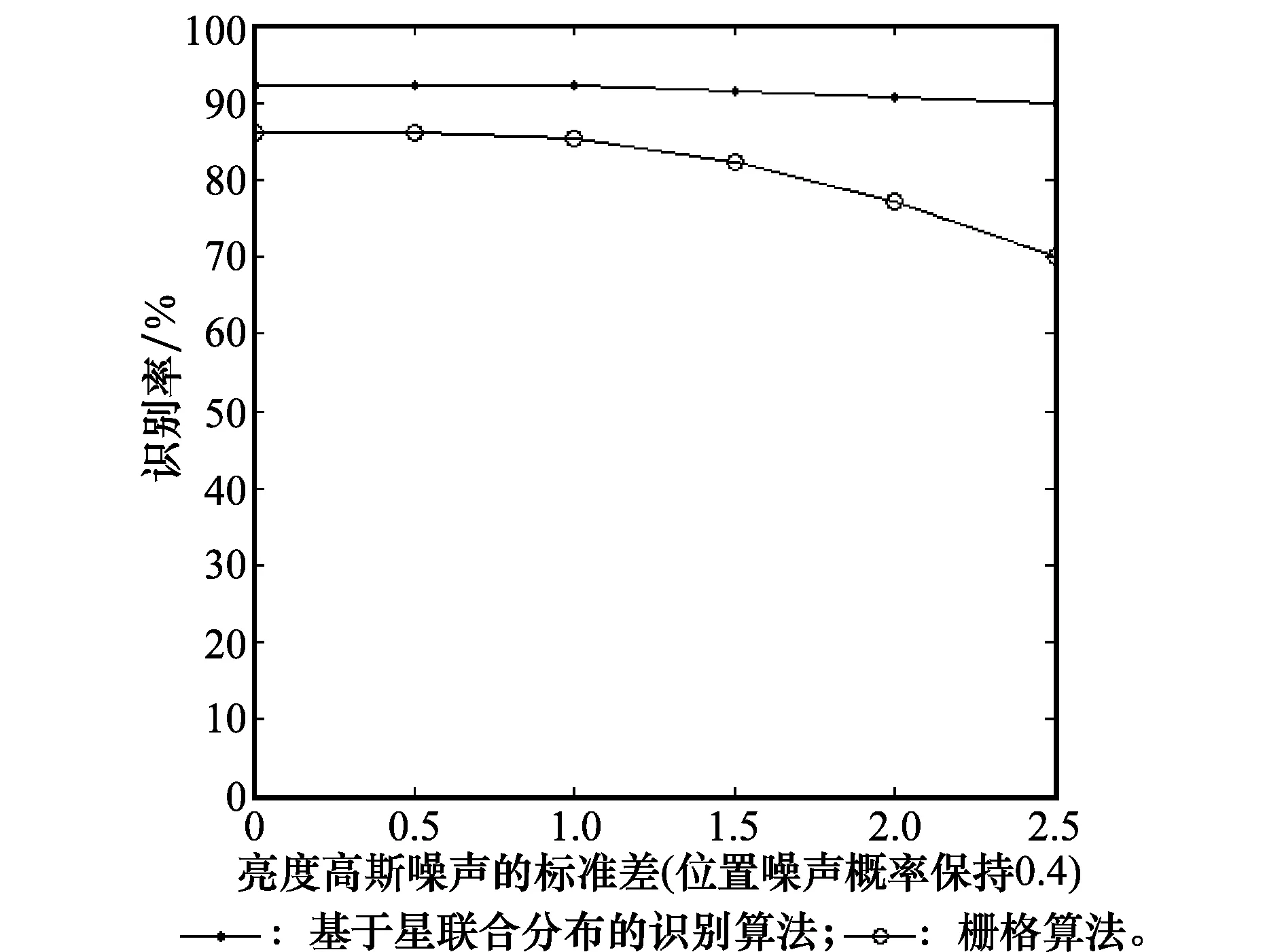
图5 加入亮度及位置噪声的情况下,栅格算法和基于星联合分布的识别算法的识别率变化 Fig.5 Change of recognition rates of grid algorithm and recogntion based on mutual star distribution withmagnitude and position noise added

亮度噪声标准差识别正确率/%栅格算法基于星联合分布的识别086．192．10．586．192．11．085．392．11．582．291．52．077．290．82．569．990．0

图5及表2中的结果表明,栅格算法对亮度噪声敏感,在位置噪声不变的情况下,随着亮度高斯噪声的标准差由0增加至2.5,其识别率下降了16.2%。而基于星联合分布的识别方法的识别率仅下降了2.1%,基本不受亮度噪声的影响。

2.3 伪星及缺失星存在时的性能

为了研究观测星图中存在伪星及缺失星的情况下,提出的识别方法的性能,在观测星图中的随机位置增加了伪星,也将随机选定的观测星图中的星进行了删减。表3及表4分别为在不同数量的伪星及缺失星存在的情况下,星图识别的正确率。

表3 伪星数量增加时不同识别算法的识别正确率

表4 缺失星数量增加时不同识别算法的识别正确率

根据仿真实验的结果,基于星联合分布的识别算法比栅格算法具有更强的鲁棒性和稳定性,并且,在不同种类的星图噪声存在的情况下,这一方法也具有高识别率。

3 存储容量和运算量

星图识别所消耗的存储空间主要用于存储导航星库数据。对于具备M颗星的导航星库,栅格算法将M个大小为g×g的栅格所对应的二进制数矩阵储存在Mg2bits大小的空间中,在M=9 082,g=40[9]的条件下约1.7M。提出的算法需要为每颗星存储模式向量,每个向量由5个特征(long double, 16 bytes)构成,所需的总存储容量为5M×16 bytes=709 KB。

进行全天星图识别所需要的时间是衡量星图识别方法的指标之一[15]。时间越短,运算量越小,表明方法的性能越好。

栅格算法对一幅星图进行识别的运算量为O(Mg2),在不考虑划分星图为多边形集合消耗内存的条件下,基于星联合分布的识别方法为O(M)。在仿真条件下,基于星联合分布的识别方法实际运行一次占用内存约为5.7M,这样的运算量在如今的计算机设备条件下是可行的。

4 结 论

将星图根据星联合分布特征划分为多边形的集合,是将星点之间的位置关系放大,这样就使提取的星模式特征相比于星角距等特征具有更强的稳定性。并且,基于星联合分布的识别方法比栅格类算法更充分地利用了星点在其邻域内的位置特征,在星图中存在噪声的情况下,也能保证提取出的特征变化微小。

[1] 李葆华. 用于航天器姿态控制的快速星图识别算法研究[D].哈尔滨：哈尔滨工业大学, 2006.

LI B H. Study on fast star pattern recognition algorithm applied in attitude control of spacecraft[D]. Harbin: Harbin Institute of Technology, 2006.

[2] 贾辉. 高精度星敏感器星点提取与星图识别研究[D].长沙： 国防科学技术大学, 2010.

JIA H. Star centroid estimation and star identification of high accuracy star tracker[D]. Changsha: National University of Defense Technology, 2010.

[3] 胡海东. 星图识别与组合导航滤波方法研究[D]. 哈尔滨： 哈尔滨工业大学, 2009.

HU H D. The methods of star map reconition and filtering for integrated navigation[D], Harbin: Harbin Institute of Technology, 2009.

[4] 田金文, 王黎, 郑胜. 基于恒星识别的微型航天器自主导航技术研究[J]. 红外与激光工程, 2006, 35(24): 336-342.

TIAN J W, WANG L, ZHENG S. Researching about automatic mini-aircraft navigation based on star recognition[J]. Infrared and Laser Engineering, 2006, 35(24): 336-342.

[5] 胡海东, 黄显林, 介鸣. 一种基于星体特征值的全天星图识别方法[J]. 黑龙江大学自然科学学报, 2007, 27(6): 731-735.

HU H D, HUANG X L, JIE M. An all-sky star map pattern recognition algorithm based n star eigenvalues[J]. Journal of Natural Science of Heilongjiang University,2007,27(6):731-735.

[6] 张广军.星图识别[M].北京 : 国防工业出版社, 2002:22-31.

ZHANG G J. Star recogniton[M]. Beijing, Nation Defence Industry Press, 2002:22-31.

[7] PADGETT C, KREUTZ-DELGADO K. A grid algorithm for star identification[J]. IEEE Trans. on Aerospace and Electronic Systems, 1997, 33(1): 202-213.

[8] NA M, ZHENG D N, JIA P F. Modified grid algorithm for noisy all-sky autonomous star identification[J]. IEEE Trans. on Aerospace and Electronic Systems, 2009, 45(2): 516-521.

[9] YI W J, LIU H B, YANG J K , et al. Three-dimensional grid algorithm for all-sky autonomous star identification[C]∥Proc.of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies, 2013:81-87.

[10] LEEGHIM H, BANG H. Star pattern identification technique by modified grid algorithm[J]. IEEE Trans. on Aerospace and Electronic Systems, 2007, 43(3): 1111-1116.

[11] ZHANG H, SANG H S, SHEN X B. A polar coordinate system based grid algorithm for star identification[J]. Journal of Software Engineering & Applications, 2010, 3(1): 34-38.

[12] SILANI E, LOVERA M. Star identification algorithms: novel approach & compirison study[J]. IEEE Trans. on Aerospace and Electronic Systems, 2006, 42(4): 1275-1288.

[13] PHAM M D, LOW K S, CHEN S S, et al. A star pattern recognition algorithm for satelitte attitude determination[J]. Industrial Electronics & Applications, 2012, 48(11): 236-241.

[14] SERVIDIA P, SANCHEZ PENA R S. New robust star identification algorithm[J]. IEEE Trans. on Aerospace and Electronic Systems, 2006, 42(3): 1126-1137.

[15] HO K. A survey of algorithms for star identification with low-cost star trackers[J]. Acta Astronautica, 2012, 73: 156-163.