近区低旁瓣的OFDM MIMO雷达波形设计

柏 婷, 任修坤, 郑娜娥

(信息工程大学导航与空天目标工程学院, 河南 郑州 450001)

0 引 言

随着雷达距离分辨力的不断提高,临近目标的分辨问题已经成为雷达系统的重要研究内容。衡量临近目标分辨能力优劣的主要因素是距离分辨力和距离旁瓣的大小。随着雷达工作环境的日益复杂,强杂波、干扰、多路径等因素会使传统波形匹配滤波后产生较高的距离旁瓣,导致了临近目标分辨中弱目标淹没和不同目标主旁瓣混叠的问题[1]。因此,设计低旁瓣的雷达发射波形成为了亟待解决的问题。

多输入多输出(multiple input multiple output, MIMO)雷达具有波形分集优势,在波形设计方面自由度大,与传统雷达相比能获得较高分辨率和参数识别能力[2-3],在临近目标分辨方面潜力巨大。MIMO雷达一般采用相互正交的发射波形来抑制目标回波之间的干扰,将正交频分复用(orthogonal frequency division multiplexing, OFDM)技术运用到MIMO雷达中[4],可以直接解决正交波形的设计问题,同时实现波形分集和频率分集。另外,OFDM信号还具有高分辨性能和波形设计灵活的特点[5]。因此,研究如何抑制OFDM MIMO雷达的距离旁瓣为解决临近目标分辨问题提供了新的思路。

针对OFDM MIMO雷达的距离旁瓣抑制问题,文献[6]直接采用发射波形的自相关和互相关函数的加权组合作为目标函数,运用遗传算法(genetic algorithm, GA)实现旁瓣抑制。文献[7]在设计低旁瓣波形时深入分析了FD-LFM MIMO雷达的模糊函数,针对3种高旁瓣类型及其出现原因,综合采用加窗和失配处理进行旁瓣抑制,但该方法会损失信噪比;在文献[6]的基础上,文献[8]重点研究了OFDM LFM信号空域合成后的旁瓣抑制问题,建立了空时优化模型,结合GA和序列二次规划法(sequential quadratic programming, SQP)进行优化,得到了较好的旁瓣特性,但该算法往往需要多次迭代,计算效率较低。

上述方法都是对全部距离旁瓣进行抑制,但在分辨临近目标时,不同目标回波序列到达时间的最大差值,都远小于发射序列的持续时间[9]。因此,感兴趣的距离单元不再是所有距离旁瓣,而更关注近区距离旁瓣。近区旁瓣抑制问题在MIMO雷达中的研究较少,文献[10]考虑了传统雷达的特定区间旁瓣抑制问题,运用非线性最小化的子空间信赖域方法进行优化,但该算法在波形序列较长时可能无法实现。文献[11]创造性地提出了适用于MIMO雷达的WeCAN算法,以最小化加权积分旁瓣水平为准则,在恒模约束条件下利用快速傅里叶变换进行迭代,实现了特定区间的旁瓣抑制,抑制性能良好,该方法的不足在于运算量巨大。

针对上述问题,本文提出了一种基于近区距离旁瓣抑制的OFDM MIMO雷达波形设计方法。首先,构造一组基于相位编码调制(phase coded modulation,PCM)的OFDM MIMO雷达发射波形集,综合考虑各天线发射波形的积分旁瓣水平(integrated sidelobe level,ISL),利用极小化极大(min-max)思想优化近区ISL最大的天线发射波形,以发射波形恒模为约束,最小化该天线波形的ISL来构造目标函数;然后,利用发射波形与相位的对应关系,将相位参量作为优化对象,借此把目标函数转化为无约束优化问题;最后,推导了目标函数梯度解析式,并利用BFGS算法求解该优化问题。仿真结果验证了本文方法的有效性。

1 信号模型

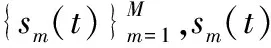
图1 OFDM MIMO雷达发射示意图Fig.1 Transmission schematic of OFDM MIMO radar

第m根天线上的编码信号为

(1)

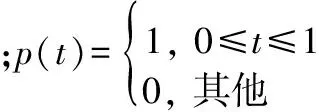
综上,待设计的编码矩阵为

S=[s1,s2,…,sM]∈CN×M

(2)

式中

sm=[sm(1)sm(2) …sm(N)]T

(3)

2 近区距离旁瓣抑制的波形设计

2.1 建立目标函数

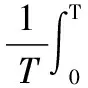
(4)

式(4)保证了任意两子载频之间的正交性,故OFDM信号通过频域正交便可实现MIMO雷达各天线发射信号正交,每根天线上的发射信号在接收端都可依赖正交性分离开,所以不再需要优化天线信号之间的互相关函数来提高其正交性,则本文优化的目标是感兴趣距离单元的旁瓣特性。在此,引出发射信号的距离模糊函数定义:

(5)

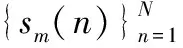
m=1,2,…,M；k=0,1,…,N-1

(6)

用每根天线发射信号的ISL表征自相关旁瓣的大小,ISL表示为

(7)

对于MIMO雷达的距离旁瓣抑制问题,文献[11]中采用所有天线ISL之和作为目标函数进行优化求解,但是这种构造方式无法保证每根天线的自相关旁瓣都最小。针对此问题,本文运用min-max思想,最小化如下准则:

max(ISLm)

(8)

s.t. |sm(n)|=1,m=1,2,…,M;n=1,2,…,N

(9)

式中

(10)

考虑到OFDM信号进行了相位编码调制,sm(n)=ejφm(n)(m=1,2，…,M;n=1,2，…,N),其中,φm(n)为相位参数,Φm=[φm(1)φm(2) …φm(N)]是第m根天线的相位参数向量。将其代入式(9),将相位参数φm(n)作为优化变量,则上述问题可以转化为无约束优化问题。综上,本文建立优化模型如下:

(11)

式中

(12)

2.2 基于BFGS算法的优化方法

上述优化模型属于二次优化问题,本文采用基于拟牛顿算法的优化算法。Broyden-Fletcher-Goldfarb-Shanno (BFGS)算法是目前最有效的拟牛顿算法之一,其基本思想是,在牛顿算法中用Hesse矩阵的近似矩阵来取代Hesse矩阵[13],以确保收敛速度,并提高计算效率。同时,考虑到不同环境下待优化的相位编码序列长度不同,本文在待优化序列长度较短时,采用BFGS算法,保证良好的旁瓣抑制效果;序列长度较长时,采用有限域BFGS(limited-memory BFGS, LBFGS)算法,限定其内存大小,消除序列长度增长导致的算法复杂度增大的影响,保证其算法效率,适应实际环境。下面推导式(12)的梯度表达式:

(13)

其中

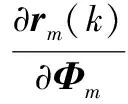
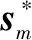
(14)

(15)

式中,⊙表示矩阵的Hadamard积。

综上所述,本文针对近区旁瓣抑制的波形设计算法步骤如下:

步骤1根据实际情况设定抑制单元范围[1,P],给定终止误差0≤ε≤1;

步骤3根据式(7)计算每根天线的ISL,由式(11)、式(12)求出目标函数f(Φ0);

步骤4由式(13)～式(15)求出目标函数的梯度g0;

步骤5判断待优化序列长度N,若N<1 500,则采用BFGS算法,若N>1 500,采用LBFGS算法;

步骤6若当前序列满足停止条件,重复步骤3～步骤6,直到所有天线均满足停止条件;否则,重复步骤5直至当前天线信号编码相位满足停止条件;

步骤7将得到的码元序列代入式(1),求出发射波形序列。

其中,步骤5的优化算法具体流程见图2。

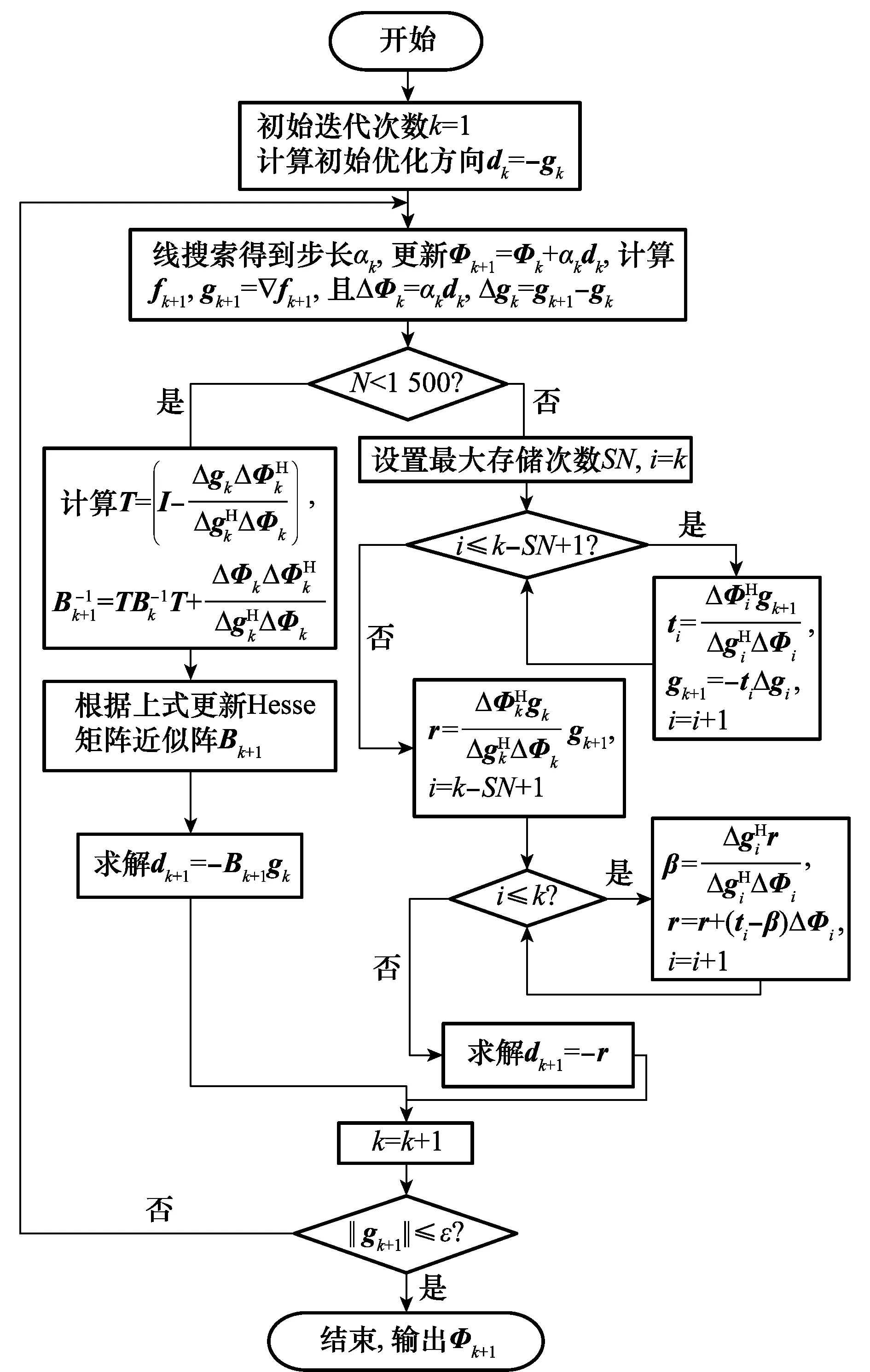
图2 步骤5算法流程图Fig.2 Flow chart of step 5

2.3 算法性能分析

值得指出的是,本文算法的主要计算量为迭代操作,在每次迭代中计算式(11)的算法复杂度约为O((2N-P)(P-1)/2),计算式(13)的算法复杂度约为O(2PN),BFGS算法中更新Hesse矩阵近似阵Bk的复杂度约为O(N2),因此本文算法总的复杂度约为O(M((2N-P)(P-1)/2+2PN+N2))。文献[8]采用GA和SQP算法,GA算法的运算复杂度与种群大小、遗传代数等有关,故在此不通过理论分析计算其算法复杂度,着重在仿真中比较其运行时间。对比文献[11],优化过程需要2MN次2N点的FFT运算和2N次M×N维矩阵的奇异值分解(singular value decomposition, SVD),则其算法复杂度约为O(MN2log22N+N4)。故与现有算法相比,本文算法复杂度较低,可较好地满足系统需求。

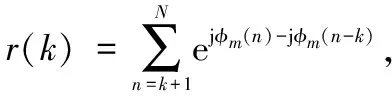
3 仿真及结果分析

本节仿真实验考虑M=4的OFDM MIMO雷达系统,选择文献[8,11]作为本文的对比算法。文献[11]中所提算法,为经典的MIMO雷达特定区间旁瓣抑制算法;文献[8]中所提算法,是OFDM MIMO雷达全部距离旁瓣抑制的常用算法。为了定量描述旁瓣抑制水平,采用待优化区间平均旁瓣深度、品质因数(merit factor, MF)、迭代次数、耗时作为算法评价指标。其中,MF表征距离模糊函数的主瓣能量与旁瓣能量和的比值,具体定义为

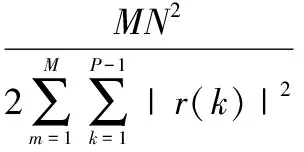
(16)

仿真1检验算法收敛性能。算法的收敛性能是设计一个迭代算法的基本要求,而其局部收敛速度是衡量一个算法好坏的重要指标。从理论上讲,BFGS算法继承了Newton方法的快速收敛性能。图3给出了本文算法的收敛性能测试结果,图3(a)表示N=100,P不同时收敛性能的比较,可以看出,不同P值并不影响收敛速度,本文波形设计算法均从第10～20次迭代后就趋于稳定;图3(b)表示P=39,N不同时收敛性能的比较,可以看出,收敛速度基本不因N的变化而变化,仍然在10～20次迭代后趋于稳定。说明本算法收敛性能良好,实验结果和理论符合较好。

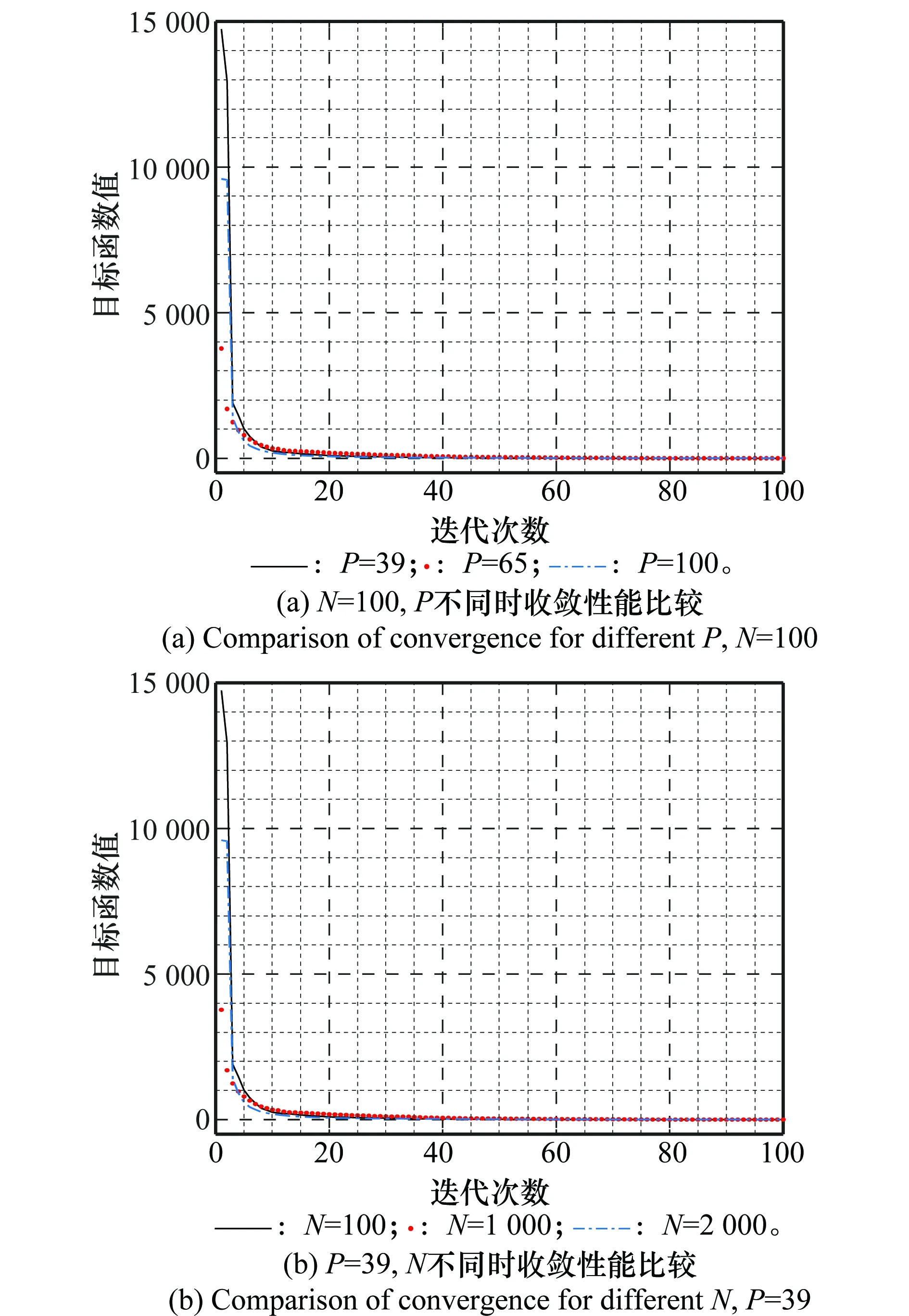
图3 算法收敛性能Fig.3 Iteration convergence

仿真2检验波形设计算法的旁瓣抑制效果。假设每根天线序列长度为N=100,初始序列采用Golomb编码序列。以距离模糊函数的0延迟为中心,对我们感兴趣的距离旁瓣区间进行抑制,分别选取[1,39]、[1,65]和全部旁瓣作为抑制区间。图4给出了抑制区间为[1,39]时的距离模糊函数,可以看出,本文设计算法的距离旁瓣极低,达到了-170.78 dB,优于文献[11]算法的-132.50 dB。从表1的详细对比中能够看到,本文算法的耗时和迭代次数都要远远小于文献[11]算法,算法复杂度低,与理论分析吻合。MF远高于文献[11]算法。图5和图6分别给出了抑制区间为[1,65]和全部距离旁瓣抑制的距离模糊函数图,从图5可以看出,当抑制区间大于全部距离单元的一半时,本文算法和文献[11]算法的距离旁瓣抑制性能都有大幅下降,只能达到-45 dB左右,抑制性能基本平齐,但是本文算法的计算复杂度还是远低于文献[11]。在图6的全部旁瓣抑制当中,本文算法的旁瓣抑制性能和文献[11]算法基本持平,在-30 dB范围内。但是对比文献[8],旁瓣深度只有-24.74 dB,耗时也更长,故本文算法的旁瓣抑制性能和算法复杂度都要比文献[8]算法的性能更好。

图4 距离模糊函数(抑制区间为[1,39]) 图5 距离模糊函数(抑制区间为[1,65]) 图6 距离模糊函数(抑制区间为[1,100]) Fig.4 Range ambiguity function(the interval Fig.5 Range ambiguity function(the interval Fig.6 Range ambiguity function(the interval of suppression is [1,39]) of suppression is [1,65]) of suppression is [1,100])

抑制区间方法[1，39]本文算法文献[11][1，65]本文算法文献[11][1，100]本文算法文献[11]文献[8]耗时/s3．63183．819．31566．159．665．71165．96迭代次数11915132721447217617245741001所求区间平均旁瓣/dB-170．78-132．50-45．86-47．43-36．21-38．69-24．74MF8．56×10141．15×1011220．01272．4215．8015．531．04

仿真结果表明,需抑制距离旁瓣的范围小于距离单元的一半时,本文设计算法可以很好地抑制旁瓣,并且算法复杂度较低,能够达到分辨临近目标的要求。但是当区间大于全部旁瓣的一半时,本文设计波形抑制效果有所下降,与理论分析结果吻合。所以,本算法在近区旁瓣抑制方面更有优势。

仿真3检验不同初始序列对旁瓣抑制效果的影响。本文选择了不同类型的相位编码序列进行对比[14],第一类是基于传统线性调频信号的相位变化的多相编码序列;第二类是伪随机编码序列。分别选择Golomb序列、Frank序列、Chu序列、P4序列、伪随机多相编码序列作为初始编码序列。序列长度N=100,感兴趣的抑制区间为[1,39],观察优化结果与初始编码序列的关系,结果见表2。

由表2可知,初始序列的相位编码形式对旁瓣抑制效果的相对影响不大,不同初始序列优化后旁瓣深度均能达到-160 dB以下,但是绝对深度差最大达到了20 dB,MF也有较大差异,其中,Golomb序列在旁瓣深度和MF方面表现最佳。实验结果可知,本文方法对初始序列的依赖性不大,但是在旁瓣深度要求极高的情况下还是应妥善选择初始序列。

表2 初始序列类型对旁瓣抑制的影响

仿真4检验序列长度对旁瓣抑制效果的影响。选择Golomb序列作为初始序列,序列长度分别选择N=50,100,200,500,1 000,2 000,感兴趣的抑制区间为[1,39],图7给出了旁瓣抑制效果的对比情况。表3列出了具体衡量参数值。

图7 序列长度对旁瓣抑制效果的影响Fig.7 Range sidelobe suppression effect of different lengths of sequence

序列长度平均旁瓣深度MF耗时/s迭代次数50-39．424376．601．5193100-189．494．44×10183．65106200-183．051．01×10188．78126500-182．559．00×101765．551571000-187．592．87×1018339．001722000-106．822．41×10102822．35400

由图7和表3可知,当序列长度N=50时,待抑制区间长度P>(N+1)/2,平均旁瓣深度只能达到-39.42 dB,符合理论分析结论;当2P1 500时,为了提高运算效率,采用LBFGS算法进行优化,故牺牲了一部分旁瓣性能,但仍能达到-100 dB以下。结果表明,本文算法在满足P≤(N+1)/2时,对于不同序列长度要求均能设计出极低近区旁瓣的发射波形。

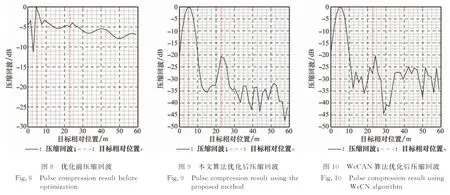
仿真5检验优化后波形对强目标旁瓣掩盖下的弱目标的检测能力。雷达的搜索、跟踪等操作通常在规定的距离窗上进行,称为接收窗。接收窗内所有目标回波被接收并且传输给匹配滤波器进行脉冲压缩[15]。假设发射信号脉冲宽度为T=1 μs,初始序列为Golomb序列,序列长度N=100,感兴趣的距离单元为P=39,雷达显示接收窗的宽度为cTP/2N=58.5 m,接收窗内目标数为2,强弱目标在接收窗内的相对距离分别为5 m和23 m,强弱目标回波功率比为20 dB。图8给出了优化前信号的压缩回波,可以看到,在弱目标位置处无法分辨目标有无,弱目标被强目标回波旁瓣完全掩盖。图9为本文算法优化后信号的压缩回波,两目标位置处回波峰值明显,弱信号主瓣峰值比回波旁瓣峰值高出11.82 dB。实验结果表明,优化前压缩回波中强目标的旁瓣基本将临近弱目标完全掩盖,无法分辨。当采用本文算法进行优化后,弱目标得以凸显,强弱目标均可被检测。图10为WeCAN算法优化后的波形,可以看到,强弱目标虽然可被检测,但弱信号主瓣峰值只比左侧临近旁瓣峰值高出3.96 dB,故本文算法在强目标旁瓣掩盖下的弱目标检测方面具有一定优势。

4 结 论

本文提出了一种基于近区距离旁瓣抑制的OFDM MIMO雷达波形设计方法,能够有效解决临近目标分辨中近区旁瓣过高的问题,同时兼顾了雷达的高分辨性能。该方法灵活应用BFGS方法求解恒模的发射波形矩阵,具有良好的近区旁瓣抑制效果和运算效率。仿真结果表明,优化后的发射波形近区距离旁瓣较低,当待设计的编码序列较长时,会牺牲一部分旁瓣特性换取计算效率,但对旁瓣深度影响不大,能保证良好的临近目标分辨性能;并且,本文算法对初始编码序列形式依赖性较小,收敛速度较快,运算复杂度小,避免了功率峰均比过高的问题,在实际应用中具有一定参考价值。

[1] 臧会凯, 周生华, 刘宏伟, 等. 应用正交码组信号的传统雷达距离旁瓣抑制方法[J]. 电子与信息学报, 2014, 36(2):445-452.

ZANG H K, ZHOU S H, LIU H W, et al. Range sidelobe suppression for conventional radar using orthogonal waveforms[J]. Journal of Electronics & Information Technology, 2014, 36(2):445-452.

[2] FISHLER E, HAIMOVICH A, BLUM R, et al. MIMO radar: an idea whose time has come[C]∥Proc.of the IEEE Radar Conference, 2004:71-78.

[3] 陈浩文, 黎湘, 庄钊文.一种新兴的雷达体制——MIMO雷达[J].电子学报,2012,40(6):1190-1198.

CHEN H W, LI X, ZHUANG Z W. A rising radar system——MIMO radar[J]. Acta Electronica Sinica, 2012, 40(6):1190-1198.

[4] DONNET B J, LONGSTAFF I D. Combining MIMO radar with OFDM communications[C]∥Proc.of the IEEE Radar Conference, 2006:37-40.

[5] 霍凯, 赵晶晶. OFDM新体制雷达研究现状与发展趋势[J]. 电子与信息学报, 2015, 37(11):2776-2789.

HUO K,ZHAO J J. The development and prospect of the new OFDM radar[J]. Journal of Electronics & Information Technology, 2015, 37(11):2776-2789.

[6] ZHANG Y, WANG J. OFDM-coded signals design for MIMO radar[C]∥Proc.of the IEEE International Conference on Signal Processing, 2008:2442-2445.

[7] DAI X, XU J, YE C, et al. Low-sidelobe HRR profiling based on the FDLFM-MIMO radar[C]∥Proc.of the IEEE Asian and Pacific Conference on Synthetic Aperture Radar, 2007:132-135.

[8] LI H, ZHAO Y, CHENG Z, et al. Orthogonal frequency division multiplexing linear frequency modulation signal design with optimised pulse compression property of spatial synthesised signals[J].IET Radar, Sonar & Navigation, 2016, 10(7): 1319-1326.

[9] STOICA P, HE H, LI J. New algorithms for designing unimodular sequences with good correlation properties[J]. IEEE Trans.on Signal Processing, 2009, 57(4): 1415-1425.

[10] 李风从, 赵宜楠, 乔晓林. 抑制特定区间距离旁瓣的恒模波形设计方法[J]. 电子与信息学报, 2013, 35(3):532-536.

LI F C, ZHAO Y N, QIAO X L. Constant modular waveform design method for suppressing range sidelobes in specified intervals[J].Journal of Electronics & Information Technology,2013,35(3): 532-536.

[11] HE H, STOICA P, LI J. Designing unimodular sequence sets with good correlations: including an application to MIMO radar[J]. IEEE Trans.on Signal Processing, 2009, 57(11):4391-4405.

[12] MEHANY W. Design discrete frequency coding waveform based OFDM for MIMO-SAR[J]. International Journal of Information and Electronics Engineering, 2015, 5(2):126-130.

[13] LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization[J]. Mathematical Programming, 1989, 45(1):503-528.

[14] SKOLNIK M I. Radar handbook[M].2nd ed. New York: McGraw-Hill,1990:408-415.

[15] 巴塞姆·马哈夫扎. 雷达系统设计Matlab仿真[M]. 北京:电子工业出版社, 2009.

MAHAFZA B. Matlab simulations for radar system design[M]. Beijing: Publishing House of Electronics Industry, 2009.