基于Lorenz混沌的MIMO雷达信号设计及性能分析

张 民, 李宗浩, 高 明

(西安电子科技大学物理与光电工程学院, 陕西 西安 710071)

0 引 言

多输入多输出(multiple input multiple output, MIMO)雷达是相较于相控阵等传统雷达的一种新体制雷达,与相控阵雷达各阵元发射相同信号不同,其对互相正交的信号进行全向发射,并以接受端匹配滤波的形式对不同的信号分量进行分离,从而提高雷达的搜索和检测性能[1]。所以正交波形的设计对MIMO雷达具有重要作用[2],雷达信号的低自相关旁瓣和低互相关峰值(cross-correlation peak, CP)能够提高脉冲压缩能力,以减小不同目标回波信号之间的相互干扰,优化回波信号的相关匹配滤波处理,从而提高目标检测性能。

目前,有多种正交波形能够被MIMO雷达采用,如基于正交频分复用(orthogonal frequency division multiplexing, OFDM)的正交线性调频(linear frequency modulation, LFM)信号(OFDM-LFM)、非线性调频信号、正交多相码、正交离散频率编码波形[3-7]。文献[6]分析了信号的自相关及互相关峰值电平进,并借助遗传算法进行优化,获得了更低互相关峰的优化离散频率编码波形(discrete frequency coded waveform, DFCW)。文献[7]在设计DFCW序列时为了克服遗传算法容易陷入局部优化的缺点,引入模拟退火算法得到一种改进的混合遗传模拟退火算法,提高了优化算法效率。

近年来,混沌理论在电力系统、通信、经济、电子工程等方面取得了巨大的发展,混沌序列也被用于正交波形的设计中。文献[8]主要探讨了将混沌应用于MIMO雷达波形设计的可行性,深入研究基于混沌理论的MIMO雷达正交波形设计问题,归纳了将混沌应用于正交波形设计的优势所在以及混沌理论在雷达信号设计方面的应用研究;文献[9-10]采用离散混沌系统设计了离散频率编码序列,分析了混沌系统参数对频率序列和最终波形的自相关和互相关性能的影响;文献[11]采用连续混沌Lorenz系统设计正交波形,分析了Lorenz系统变量的特征,将Lorenz系统的变量x进行调制,设计出具有良好自相关性能和互相关性能的正交信号。文献[12]把Lorenz混沌序列与频率调制信号结合起来,将Lorenz序列的变量x作为调频项,设计出具有复杂结构的正交频率调制信号。

混沌系统初始值的微小变化可产生完全不同并且相关性能良好的混沌序列,这使得基于混沌系统的正交波形可以能够满足MIMO雷达性能需求[12]。目前,混沌系统主要分为两种,一种是连续混沌系统如Lorenz系统;另一种是离散混沌系统如Bernoulli系统、Logistic系统等。离散混沌系统映射简单,参数较少,设计自由度小。基于以上分析,本文将连续混沌序列Lorenz系统用于离散频率编码线性调频信号的优化设计,应用Lorenz混沌系统设计编码序列,相较于遗传算法和退火算法等优化算法拥有更低的复杂度,并使得信号拥有不可预测、无周期性等特点,提高信号的抗干扰和抗截获性能。最终仿真了该信号匹配滤波性能,得出良好的结论。

1 Lorenz混沌系统

Lorenz系统由式(1)所示的方程组描述,该方程由美国著名气象学家Lorenz提出:

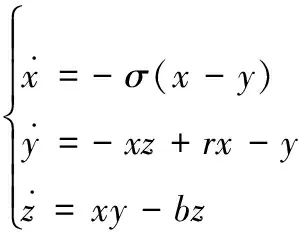
(1)

当式(1)中3个参数σ,r,b满足式(2)时,Lorenz系统会出现混沌解。

(2)

采用四阶龙格库塔法求解洛伦兹方程组,可求得3个状态变量x(t),y(t)和z(t)。变量x(t)在信号处理特性上优于y(t)和z(t)[13],所以后面均采用变量x(t)设计正交雷达信号。图1是根据式(1)所得的Lorenz系统的吸引子,给出了它的三维图形,图中Lorenz系统3个变量都是有界的,吸引子上也没有交叉点,其状态轨迹反复折叠形成一个复杂的带状区域。图2为Lorenz系统3个状态变量时域图,图中3个变量都是非周期的,并且Lorenz系统也体现出其初值敏感性,初始变量相差0.1,这种微小变化使得混沌状态变量的解出现很大变化,混沌系统的以上特性对设计多组正交信号非常有利。

图1 Lorenz系统吸引子Fig.1 Lorenz attractors

图2 Lorenz系统状态变量变化曲线Fig.2 Lorenz variable change curve

2 DFCW-LFM信号设计

2.1 DFCW-LFM信号模型及相关函数分析

良好的互相关特性是DFCW信号的一个突出优点,因而在MIMO雷达系统中的应用十分广泛。然而鉴于其自相关性能上的劣势,如自相关旁瓣峰值(autocorrelation sidelobe peak,ASP)高达-13.2 dB,经常在信号检测中很容易出现将信号的自相关旁瓣误判为目标的虚警现象;但当信噪比较低时,弱目标信号则可能被旁瓣峰值淹没而发生漏警。因而在以上很多类似情况下,传统的DFCW信号无法满足实际中MIMO雷达对回波信号的检测需求。根据文献[6]对DFCW信号的相关分析,ASP的具体表现与频率编码顺序之间的关系不大,并且随着编码长度的增加,CP呈现下降趋势,ASP依然保持不变,所以将LFM引入到离散频率调制,在各子脉冲之间及子脉冲内部分别采用离散频率调制和线性频率调制的方式,得到的混和波形(DFCW-LFM)有望减小ASP,信号模型如下:

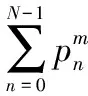
(3)

其中

(4)

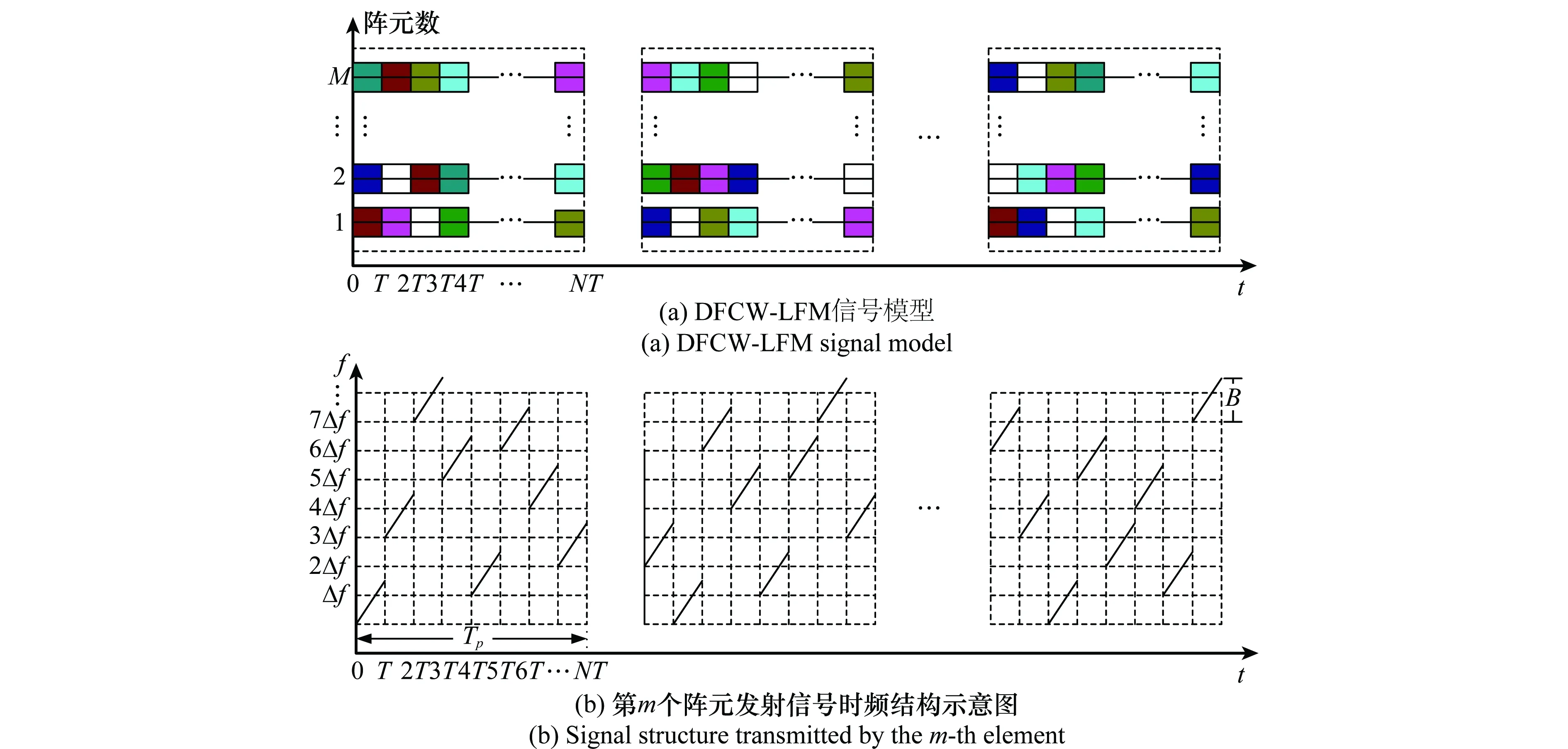
图3 DFCW-LFM雷达信号时频结构示意图Fig.3 Structure of DFCW-LFM signal

{x1,x2,x3,…,xN}→{fm1,fm2,fm3,…,fmN}

图4 基于混沌序列的离散频率编码信号生成方案Fig.4 Generation of discrete frequency coded signalsbased on chaotic sequences

DFCW-LFM信号中第个脉冲的自相关函数[14-15]为

(5)

将上述自相关函数分为两部分,一部分为LFM信号所产生自相关函数,记为R1(τ):

(6)

另一部分为栅瓣,记为R2(τ):

(7)

R2(τ)的主瓣和栅瓣将会出现在的整数倍处[14],即

τ=int·T,int=0,±1,±2,…

(8)

如图5所示,当R2(τ)的栅瓣出现的时间点与R1(τ)的零点重合时,那么栅瓣峰值将会被抵消,并且R1(τ)的旁瓣将受到R2(τ)的限制而降低,混沌离散频率编码与线性调频混合信号(chaotic discrete frequency coded waveform with linear frequency modulation, CDFCW-LFM)的旁瓣峰值相较于DFCW信号有所减小,并且与带宽和脉冲宽度的乘积BT及脉冲间隔和脉冲宽度的乘积Δf·T相关。

2.2 参数选择及性能分析

子脉冲个数N取值为16,32,48,64(每次测试均为100次试验平均值)。子脉冲宽度T=5×10-6s,图6～图8分别展示了ASP、CP和主瓣宽度(t3 dB)随着N和BT积的变化幅度。为满足条件R2(τ)的栅瓣出现时间点与R1(τ)的零点重合。当Δf·T=1时,BT积变化范围为10到60,步进宽度为10;当Δf·T=2时,BT积变化范围为12到108,步进宽度为12;当Δf·T=3时,BT积变化范围为36到144,步进宽度为36;当Δf·T=4时,BT积变化范围为32到160,步进宽度为32。

图5 R1(τ)(实),R2(τ)(虚)和DFCW-LFM自相关函数Fig.5 R1(τ)(solid line),R2(τ)(dotted line) and the autocorrelation function of DFCW-LFM

图6 ASP随BT积、Δf·T和序列长度N的变化幅度Fig.6 ASP changed with BT,Δf·T and N

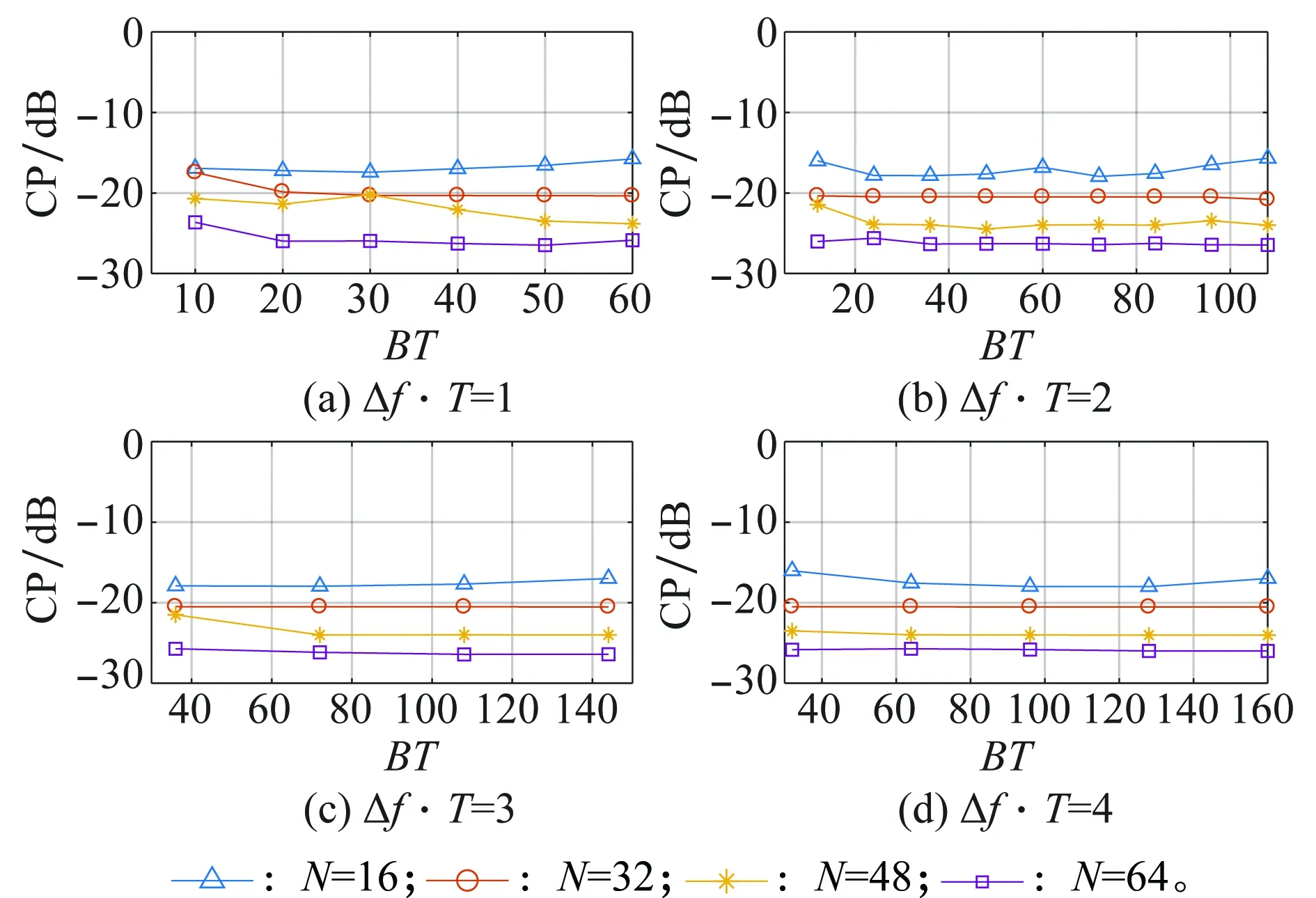
图7 CP随BT积、Δf·T和序列长度N的变化幅度Fig.7 CP changed with BT,Δf·T and N

图8 主瓣宽度随BT积、Δf·T和序列长度N的变化Fig.8 Main lobe changed with BT,Δf·T and N

图6～图8分别展示了信号自相关函数、互相关函数和主瓣宽度与信号子脉冲长度N、BT积和Δf·T之间的关系。我们可以得出以下结论:

(1) 在DFCW信号中引入线性频率调制后,ASP随着BT积增大而降低,并逐渐趋于稳定;

(2) ASP、CP随着N的增加而降低,而互相关函数只与N相关,BT积的变化对互相关函数影响很小,与文献[6]中提出的结论信号互相关函数随编码长度增加而减小相符合;

(3) 主瓣宽度随BT积和N的增大而减小,并逐渐趋于稳定。

3 基于混沌序列的多脉冲压缩积累

首先,对MIMO雷达的接收回波数据进行匹配滤波处理。假设接收阵元个数为Mr,由于MIMO雷达是多输入多输出雷达,因此接收端每个阵元下的匹配滤波器数目与发射阵元数相等,设为M,如图9所示,则将会得MMr路输出信号,并对其做波束形成。

图9 匹配滤波示意图Fig.9 Matched filter

传统雷达的所有发射阵元在脉冲重复周期之内均发射相同波形的信号,进而接收机对所接受到的回波信号进行处理。本文中,利用不同初值的混沌序列不相关这个特点,同一阵元发射初始值不同的混沌波形,最后在处理阶段通过脉冲压缩积累的方式来降低旁瓣对信号检测的影响。假设在K个脉冲重复周期里,目标的散射特性保持不变,接收机对K个回波脉冲信号进行脉冲压缩积累处理:

(9)

3.1 点目标仿真及分析

这里使用3组信号集进行仿真对比:内部噪声为均值为零的高斯噪声。图10展示了点目标一维距离向输出,给定参数:目标距离R=10 km,子脉冲宽度T=5×10-6s,TB=72,Δf·T=3,混沌信号子脉冲长度为16、32、48。从图10中可以得出以下结论:①回波信号自相关旁瓣随着子脉冲长度N的增加而降低,与图6的结果相吻合;②同时主瓣宽度也随着子脉冲长度N的增加而降低,与图8的结果相吻合。

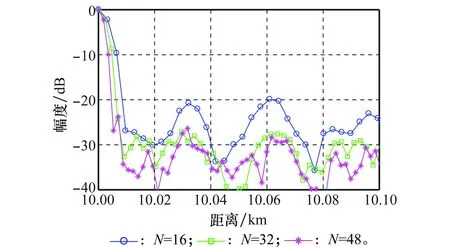
图10 单个点目标一维距离向输出对比Fig.10 One-dimensional distance image of a point target

3.2 脉冲压缩积累仿真比较及分析

通过式(5)分析得知,本文设计的混沌序列信号在经过多脉冲压缩积累后可以有效地降低自相关旁瓣及互相关的影响。两目标距离分别为R1=9.98 km和R2=10 km,μ表示两个目标散射系数比值,K表示有效脉冲重复周期内脉冲个数,其余参数选择与第3.1节相同。

3.2.1 散射系数比值μ=0.5

雷达目标通常由多个散射系数各异的目标组合在一起,检测这些不同的散射系数的目标是衡量雷达系统性能的重要指标之一。在本小节中,我们做一个强目标附近的的弱小目标检测的MIMO雷达检测性能测试。图11(a)、图11(b)分别展示了DFCW波形,CDFCW-LFM波形脉冲压缩后目标距离像结果,DFCW波形采用文献[6]中遗传算法优化所得的频率序列,其中两目标RCS幅度比值为μ=0.5。此时,两组信号都能够有效检测出强弱目标,但是DFCW波形副瓣约为-14 dB左右,明显高于本文CDFCW-LFM波形的-19 dB。

图11 双目标脉冲压缩输出对比图(μ=0.5,N=32)Fig.11 Comparison of two-target pulse compression output(μ=0.5,N=32)

3.2.2 散射系数比值μ=0.1

同样选用两组信号,其中两目标RCS幅度比值为μ=0.1,从图12中获得如下结论:随着目标散射系数比值的降低,弱目标信号逐渐降低直到被淹没在副瓣中无法检测,DFCW波形和CDFCW-LFM波形在积累前均无法检测弱目标信号,但是在将CDFCW-LFM回波信号经过脉冲积累后,图12(c)在R1处可以明显看出弱目标峰值。

图12 双目标脉冲压缩输出对比图(μ=0.1,N=32)Fig.12 Comparison of two-target pulse compression output(μ=0.1,N=32)

图13展示了ASP随脉冲数K的变化幅度,信号长度N=32,与文献[6]相同。

表1比较了DFCW波形、CDFCW-LFM波形及积累后的ASP和CP大小。通过对上述仿真结果的分析可以得出以下结论:①DFCW波形具有较高的ASP和CP,并且不随脉冲积累数变化;②DFCW波形内部进行线性频率调制后,使得ASP降低约6～7 dB,CP降低约1 dB;③再将CDFCW-LFM波形通过脉冲压缩积累处理后,ASP随着脉冲积累数的增加而降低7～12 dB,有效改善了信号的检测性能。

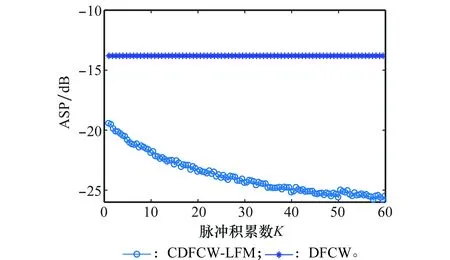
图13 ASP随脉冲积累数K变化幅度Fig.13 ASP varies with the number of accumulated pulse number K

波形最大ASP/dB平均ASP/dB最大CP/dB平均CP/dBDFCW[6]-13．75-13．92-23．34-23．45DFCW⁃LFM[15]-22．06-23．81-24．08-24．94CDFCW⁃LFM-19．85-20．93-24．53-24．84CDFCW⁃LFM32脉冲积累-24．92-25．34-26．82-27．65

4 结 论

传统的雷达信号多为确定性信号,形式单一、参数简单,为此本文提出了基于混沌序列理论的优化方法,即借助混沌的初值敏感性、不可预测性、无周期性和可再生等优点,将连续混沌序列Lorenz系统用于优化CDFCW-LFM信号,并分析了信号的各项性能,得出以下结论:①基于Lorenz混沌的CDFCW-LFM信号设计灵活,相较于遗传算法和退火算法在时间复杂度上有很大的改善;②引入混沌和LFM后的DFCW信号在信号自相关和互相关性能显著提高;③在性能方面,基于混沌序列的编码信号与传统的优化算法(如遗传算法、模拟退火算法等)所得的信号相比,可能存在一些差距。然而,在设计信号的灵活度、实时性和任意编码长度和任意波形个数的正交信号集等方面具有较大的优势和潜力。另外,利用不同初值的混沌序列不相关这个特点,通过脉冲分集和脉冲压缩积累,检测性能进一步得到提升,甚至可以超过传统优化算法所得的正交信号的性能。

[1] LI J, PETRE S. MIMO radar signal processing[M]. NJ: Wiley, 2009.

[2] ANDREW J D. Transmit signal design for mimo radar and massive MIMO channel estimation[D].West Lafayette: Purdue University, 2013.

[3] 刘波,韩春林,苗江宏. MIMO 雷达正交频分LFM信号设计及性能分析[J]. 电子科技大学学报, 2009,38(1):28-31.

LIU B, HAN C L, MIAO J H. OFD-LFM signal design and performance analysis for MIMO radar[J]. Journal of University of Electronic Science and Technology of China,2009,38(1):28-31.

[4] 张民,刘海鹏,蔡兆晖.基于组合窗的OFDM-NLFM信号设计[J].系统工程与电子技术,2016,38(2):287-292.

ZHANG M, LIU H P, CAI Z H. Design of OFDM-NLFM signal based on combined windows[J]. Journal of systems engineering and electronics, 2016,38(2):287-292.

[5] 李明, 郝明. 基于混合遗传算法的正交相位编码波形设计[J]. 信息化研究, 2007, 33(10):1-4.

LI M, HAO M. Waveform design of polyphase orthogonal code based on hybrid genetic algorithms[J]. Electronic Engineer, 2007, 33(10):1-4.

[6] 刘波, 何子述, 王海江. MIMO雷达中的DFCW设计及性能分析[J]. 电子科技大学学报, 2010, 39(5):688-691.

LIU B, HE Z S, WANG H J. DFCW signal design and performance analysis for MIMO radar[J]. Journal of University of Electronic Science & Technology of China,2010,39(5):688-691.

[7] GONG S F, DE B, PAN M H. Discrete frequency code waveform design for OAR based on HGSAA[J]. Journal of Systems Engineering & Electronics, 2013, 35(9):1854-1860.

[8] 杨进. 基于混沌理论的MIMO雷达正交波形设计与目标检测技术研究[D]. 长沙: 国防科学技术大学, 2012.

YANG J. Orthogonal waveform design and target detection for MIMO radar based on chaos theory[D]. Changsha: National University of Defense Technology, 2012.

[9] 申东,张林让,刘昕,等.用混沌序列降低MIMO雷达波形自相关旁瓣和互相关[J].西安电子科技大学学报,2012,39(5):42-46.

SHEN D, ZHANG L R, LIU X, et al. Reducing the waveform auto-correlation sidelobes and cross-correlation of MIMO radar by using chaotic sequences[J].Journal of Xidian University,2012,39(5):42-46.

[10] SHEN D, ZHOU Y, LIU X, et al. Chaotic discrete frequency coding waveform design for MIMO radar[C]∥Proc.of the IEEE International Conference on Computer and Information Technology, 2014:111-117.

[11] WILLSEY M S, CUOMO K M, OPPENHEIM A V. Quasi-orthogonal wideband radar waveforms based on chaotic systems[J]. IEEE Trans.on Aerospace & Electronic Systems,2011,47(3):1974-1984.

[12] 段军棋. 正交波形MIMO雷达信号设计及处理研究[D]. 成都:电子科技大学, 2009.

DUAN J Q. Design and processing of orthogonal waveform for MIMO radar[D]. Chengdu: University of Electronic Science and Technology of China, 2009.

[13] WILLSEY M S, CUOMO K M, OPPENHEIM A V. Selecting the Lorenz parameters for wideband radar waveform generation [J]. International Journal of Bifurcation & Chaos, 2012, 21(9):2539-2545.

[14] LEVANON N, MOZESON E. Nullifying ACF grating lobes in stepped-frequency train of LFM pulses[J]. IEEE Trans.on Aerospace & Electronic Systems, 2003, 39(2):694-703.

[15] LIU B. Orthogonal discrete frequency coding waveform set design with minimized autocorrelation sidelobes[J]. IEEE Trans.on Aerospace & Electronic Systems,2009,45(4):1650-1657.

[16] MEHANY W, JIAO L. Improved design of orthogonal discrete frequency-coding waveform based on modified genetic algorithm for MIMO-SAR[C]∥Proc.of the IEEE International Conference on Signal Processing, Communications and Computing, 2014:341-345.

[17] LI H, ZHAO Y, CHENG Z, et al. OFDM chirp waveform diversity design with correlation interference suppression for MIMO radar[J]. IEEE Geoscience & Remote Sensing Letters, 2017, PP(99):1-5.