分数阶PID自寻优控制在中频感应加热炉系统中的应用

陈 辰，李德福，聂丛楠

0 引言

感应加热设备由交流电源和感应线圈组成，电源给设备提供能量，线圈将电能装换成热能。对交流电源的控制是中频感应炉最为核心的技术，对中频电源的控制是温度控制的主要内容[1]。

与传统的其他加热炉相比，中频感应炉具有生产效率高、加热速率快、节省材料、氧化脱炭少与低耗能、加热均匀、锻模成本、无污染等优点[2]。感应加热在铸造加热中具有显著的优点，这种加热方法更有利于实现系统的自动控制，是最好的铸件加热方式，使之在国内外工业领域得到广泛的应用。因此更好的热温度控制能更好地保证加热铸件的质量，对提高经济效益有着重要的意义。

对于工业智能控制领域来说，显然是需要更加灵活以及精确的控制方法，因此，提高感应加热系统的控制性能成为了研究的关键点。本文提出了一种新的控制算法并应用到感应加热的温度控制系统中，结果表明本文方法具有较好的控制效果。

1 感应加热的基本原理

感应加热是以法拉第电磁感应现象作为基础，先把三项交流电整流成直流电，然后对整流好的直流电进行逆变，变成频率可调的交流电，最后将调节好的交流电输入感应线圈内[3]。将交流电经过感应线圈时，线圈周围会产生一个交变磁场。把金属置于这个交变的磁场内，金属内部会产生一个电势差，这个电势差会使金属中产生电涡流（这种电涡流具有中频电流的特性）而产生热量。这就是感应加热的原理。

感应加热的原理如下：

感应加热可以分为两个过程，一个是电磁感应过程，另一个是热传递的过程。电磁感应的过程可以影响热传递的过程，是感应加热中的主要过程[4]。

2 炉温控制系统的PID控制器设计

2.1 基于教与学优化算法

教与学优化算法是模仿班级教学过程的，通过教师教学和学生课后自学，以提高班级成绩，达到优化目的[5]。其算法流程图如图1所示。

图1 教与学优化算法流程图

班级中所有的成员都是优化算法中进化的个体。每个成员所学的某个科目即为一个决策变量。班级中最优秀（自适应度最高）的个体成为教师，其它个体是学员。班级种群可表示为以下形式：

式中：Xj（j=1，2，...NP）表示班级学员，NP为成员个数，d为学员的课程数目。

在教与学优化算法中，教学阶段即教师对学员授课，通过使用教师和学员平均值之间的差异性进行学习，如式（1）所示：

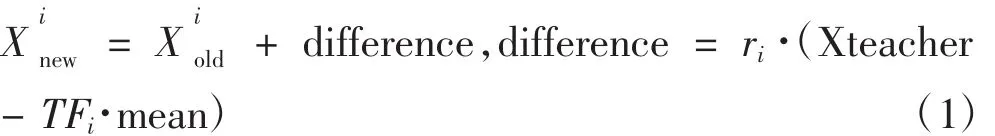
自学阶段：在班级种群中，随机挑选一个对比学员Xj，对于每一个学员Xi通过分析自身与对比学员之间的差异性进行改进。如果自身适应值优于对比学员，学员原值减去加权差异值，查漏补缺；如果自身适应值逊于对比学员，则学员原值加上加权差异值，提高自身成绩。如式（2）所示：

上式中：ri为学习步长

2.2 分数阶微积分

整数阶微积分不过是其一种特殊形式[6]。

定义分数阶微积分算子如下：

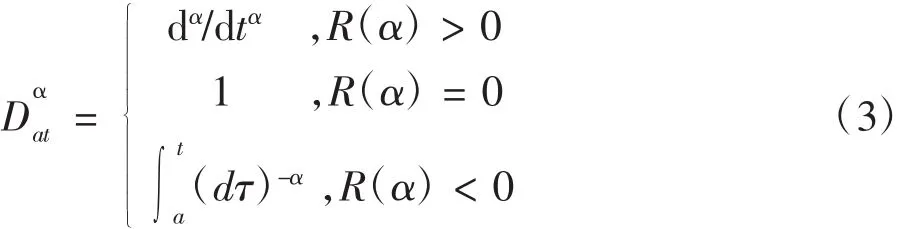
伴着分数阶微积分不断的发展，产生了许多对分数阶微积分函数的定义。如：由整数阶微积分发展而来的 Cauchy公式、Grunward-Letnikov公式、Riemann-Liouville公式以及Capotu定义。常用的分数阶微积分定义有以下两种：

（1）Grunward-Letnikov微积分定义：

（2）Riemann-Liouville微分定义：

其中，n-1＜ α ＜ 1，Γ（·）为Euler Gamma函数。其积分定义为：

其中，0＜β＜1.从以上定义可以看出，分数阶微积分具有记忆性，它与过程中所有时刻的函数值有关。

2.3 基于教与学优化算法的分数阶PID控制器

PID控制被广泛的用于工业过程控制中，由于其参数精确度直接影响着系统的稳定性，所以其参数的优化是人们一直关心的问题[7]。学者对控制器的参数优化做了大量的研究，现阶段对分数阶PID控制器的研究也趋于成熟。所谓分数阶PID控制器即是采用分数阶微积分代替传统PID控制器中的整数阶微积分。本文采用教与学优化算法对分数阶PID控制器参数进行优化，对控制器从新进行设计，对控制器结构进行优化。系统结构图如图2所示。

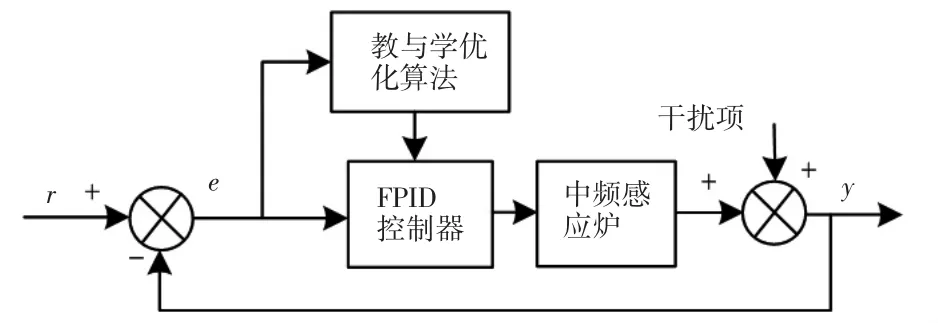
图2 基于教与学优化算法优化的PID控制系统结构图

3 仿真实验及结果分析

为了验证本文所用方法的有效性，本文利用matlab编程进行仿真，建立被控对象的数学模型，采用被控对象的传递函数进行离散化数字仿真。本文采用文献[8]中由感应加热炉建立的数学模型，传递函数如下：

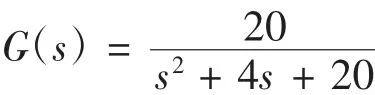
PID参数优化较常用的适应度函数主要有平方误差积分（ISE）、时间加权平方误差积分（ITSE）、绝对值误差积分（IAE）、时间加权绝对值误差积分（ITAE）。本文基于中频感应加热炉的特性选择ITAE作为最小目标函数。同时为了防止控制能量过大，对设备造成损坏，加入控制输入的平方积分[7]。适应度函数如下：

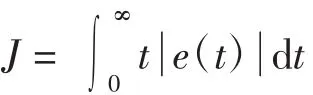
式中，e（t）为系统误差，t为时间参数。

PID控制器是由系统误差及其积分、微分线性组合而成，FPID控制器是由系统误差及系统误差的分数阶积分和分数阶微分线性组合而成。本文采用FPID算法，实现对系统的仿真，中频感应炉炉温控制系统matlab仿真图如图3所示，控制器输出为：

图3 中频感应炉炉温控制系统matlab仿真图

整体算法流程如下：

（1）设定FPID参数的上下界，并对其进行编码随机生成初始种群；

（2）算法权值初始化，设定算法各参数，设定迭代次数；

（3）由评价标准计算适应度；

（4）是否满足要求，是转（6），否转（5）；

（5）对种群进行教与学操作生成次代种群，转（3）；

（6）对种群解码，输出最优FPID参数。

本文应用教与学优化算法对FPID控制器参数进行优化，设定班级成员为50个，对各科目成绩进行编码处理，经过100代进化，其进化过程如图4所示。最优适应度指标J=246.562 8，FPID控制器最优参数为：kp=13.226 7，ki=3.889 5，kd=3.243 6.为了验证控制器最优参数的系统性能，将参数代入系统的FPID控制器，系统单位阶跃曲线如图5所示。

图4 适应度函数J的优化过程

图5 FPID控制系统单位阶跃响应

由图4可以看出，采用教与学优化算法对FPID控制器进行参数优化，具有收敛速度快，能较快寻到最优解。由图5可以看出，采用教与学优化算法寻找到的控制器最优参数，系统响应较快且系统无超调，系统性能较为优秀，可见控制器最优参数精度较高。

为了更为直观地显示本文方法的优越性，本文引入传统PID控制器做对比，同样使用教与学优化算法对其PID参数进行优化，PID控制器最优参数为：kp=19.482 1，ki=0.309 7，kd=0.126 5. 其单位阶跃曲线如图6所示。由图5和图6对比可以看出，本文控制方法较普通PID控制方法超调量降低、稳定误差降低、调整时间降低，有比较明显的优势。在实际工作中能防止超调过大而造成的设备损坏。

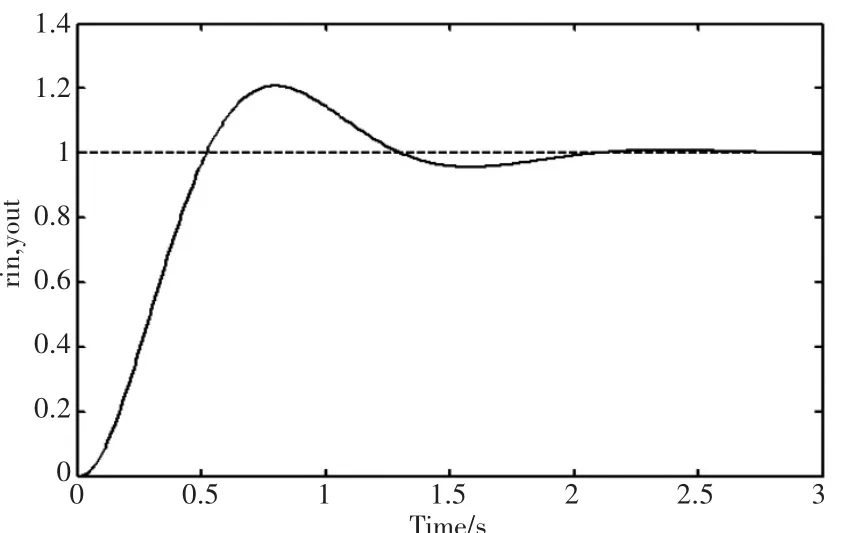
图6 PID控制系统单位阶跃响应

中频感应炉在工作时，常常由于外界室温等变化，而对感应炉正常工作产生干扰。为了验证本文控制系统的稳定性，在单位阶跃曲线稳定后加入幅值为0.1的阶跃信号作为干扰项，如图7所示。由图7可以看出，当干扰信号发出时，系统能较快对其进行矫正，本文控制系统稳定性较好，有较强的抗干扰性。

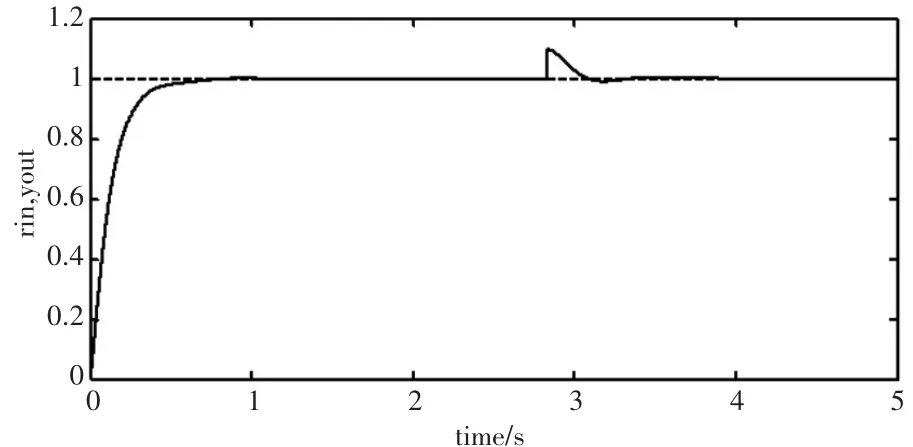
图7 加入幅值为0.1的干扰时FPID控制系统单位阶跃响应

4 结论

对于中频感应炉温度控制系统的稳定性和控制精度，采用教与学优化算法对系统的各个参数进行优化，使系统的参数更加准确，系统的稳定性得到了显著的提高。仿真实验结果表明：本方法能更加快速的得到系统参数的最优值，使得系统稳定的运行，当系统受到干扰时，也能做出快速的响应，使系统快速地回到稳定运行的状态。

[1]祁 鲲，厉 虹.基于PLC的温度控制仿真试验平台设计[J].电气技术，2013（09）：30-33.

[2]韩逸冰.高频感应加热设备感应器的设计[D].郑州：郑州大学，2013.

[3]朱龙元.电磁感应加热控制系统的设计与实现[D].成都：电子科技大学，2015.

[4]邓艳波.电磁感应加热控制电路的设计与实现[D].成都：电子科技大学，2015.

[5]何学明，苗燕楠，罗再磊.基于教与学优化算法的PID控制器参数寻优[J].计算机工程，2015（08）：313-316.

[6]武 东.基于分数阶微积分理论的控制器设计及应用[D].北京：北京理工大学，2015.

[7]刘金琨.先进PID控制MATLAB仿真[M].北京：电子工业出版社，2004.

[8]李广义.感应加热炉温度智能控制系统研究[D].洛阳：河南科技大学，2012.