一种基于混沌调频信号的稀疏雷达成像

李 松,魏中浩,张冰尘,洪 文,黎昌硕

(1.中国科学院电子学研究所,北京100190;2.微波成像技术国家重点实验室,北京100190;3.中国科学院大学,北京100190)

0 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)是一种具有全天时、全天候的高分辨成像系统。传统的合成孔径雷达需要严格遵守奈奎斯特采样定律,因此为了实现宽测绘带和高分辨率需要海量数据运算的支持,给雷达系统的计算、传输和存储性能带来巨大的负担。近年来由Donoho提出的压缩感知理论[1](Compressive Sensing,CS)使得当信号满足稀疏性或可压缩性时,能够有效利用观测目标的先验信息,从有限的观测数据中获得较高的变换域分辨率以实现信号的准确重建。CS理论框架下的雷达成像技术能在降低信号采样率的前提下提高目标图像质量,为图像分析和目标识别提供有效的信息。CS已在雷达信号处理等领域取得了广泛应用[2-3]。目前应用于稀疏雷达的典型压缩感知重建算法有迭代阈值算法[4](Iterative Thresholding Algorithm,ITA)、正交匹配追踪法[5](Orthogonal Matching Pursuit,OMP)和复近似消息传递法[6](Complex Approximated Message Passing,CAMP)等。但在稀疏雷达成像过程中,大的目标场景往往意味着巨大的计算量,交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)在凸优化问题上的效率优势[7]使其能在不影响计算精度的前提下对稀疏成像过程并行加速,大大提升计算性能。

目前合成孔径雷达在距离向的高分辨率多为通过线性调频信号(LFM)进行脉冲压缩获取的,这也就带来了雷达参数容易估计而被截获的问题。混沌序列调频信号具有良好的相关特性,类“图钉形”的模糊函数使其具有较高的测距测速能力[8]。同时,混沌序列调频信号又有类随机性,克服了线性调频信号参数容易估计的缺点。这些优点使得混沌序列调频信号在雷达成像领域取得了广泛的关注。

本文将压缩感知与混沌序列调频信号相结合,使用一种新的压缩感知重构算法对稀疏雷达进行成像。相比于传统的时域相关法,该方法能大大降低回波信号的采样率,并且能利用混沌序列调频信号的优势对目标场景精确成像。新重构算法的加入使得分布式并行运算成为可能,提升了数据处理的速度。本文首先介绍相关理论,然后给出压缩感知雷达模型,最后通过仿真试验验证其可行性。

1 混沌序列调频信号

混沌序列调频信号的波形设计主要在一维离散混沌映射的基础上进行,混沌序列调频信号的时域数学模型一般为

式中,信号频率φ(t)由混沌序列xk计算得到

用于产生混沌序列的一维离散混沌映射方法主要有Bernoulli映射、Tent映射、Logistic映射和Chebyshev映射[9]。以上4种混沌映射中,Bernoulli映射的功率谱最不平坦,同时其自相关函数的峰值旁瓣比最高。文献[9]指出在实际使用混沌序列进行信号调频时,只有Bernoulli映射序列才能得到理想的自相关特性。因此本文采用Bernoulli映射产生的混沌序列作为发射信号,其定义为

可见虽然混沌调频信号对敌方雷达系统是随机信号,但由于混沌调频信号由初始值和迭代参数唯一确定,所以它相对于系统自身来说其实是确定的,其不断变化的波形提升了雷达的隐蔽性能,图钉形的模糊函数使得混沌调频雷达可以同时无模糊地进行测距和测速[10]。这些特点使得混沌信号拥有广泛的应用前景[11]。

2 压缩感知理论和雷达成像模型

2.1 压缩感知理论

定义向量X={x1,x2,…,xN}的lp范数为

式中,当p=0时得到l0范数,表示X中非零项的个数;p=1时为l1范数,表示X中各个元素绝对值之和。

考虑一个有限长一维离散时间信号x,RN空间的任何信号都可以用N×1维基向量{ψi}的线性组合表示。由向量集{ψi}构成N×N维的基矩阵Ψ={ψ1,ψ2,…,ψN},任一信号在该基矩阵之下都可以表示为

式中,s为x的展开系数构成的N×1维列向量,且si=〈x,ψi〉,当s中只有k个非零元素时,称信号x是稀疏的。

如果对信号x的测量是在时域上进行的,那么有

式中,Φ为M×N维矩阵,称之为观测矩阵,y为测量值。当观测数量M远小于信号长度N时,由观测数据y重构x的方程是欠定的,信号x不能直接由测量值y求解。

将式(4)代入式(5)中得到

在信号稀疏或可压缩的前提下,求解欠定方程组y=As的问题转化为最小l0范数问题:

求解上述问题需要列出s中所有非零项位置的CKN种线性组合才能得到最优解。因此,求解上式是NP难问题(Non-Deterministic Polynomia,多项式复杂程度的非确定性问题),其数值计算解极不稳定。文献[12]指出当观测矩阵A=ΦΨ满足有限等距性质(Restricted Isometry Property,RIP)时,上述问题可以等价为更简单的l1范数优化问题:

l1范数下的优化问题又称为基追踪(Basis Pursuit,BP)问题,目前基追踪的压缩感知重构算法主要分为贪婪算法和凸优化算法两大类,其中凸优化算法比贪婪算法所求的解更加精确,但是需要更高的计算复杂度。

在稀疏雷达成像过程中,大目标场景的重构往往意味着巨大的计算量,传统稀疏算法模式下的集中式计算可能需要耗费相当长的时间来完成。交替方向法(Alternative Direction Method of Multipliers,ADMM)是一种求解优化问题的计算框架,适用于求解分布式凸优化问题。ADM M通过分解协调(Decomposition-Coordination)过程,将大的全局问题分解为多个较小、较容易求解的局部子问题,并通过协调子问题的解而得到全局问题的解。ADM M 最早分别由Glowinski和Marrocco、Gabay和Mercier于1975年和1976年提出,并被Boyd等于2011年重新综述并证明其适用于大规模分布式优化问题[13]。ADMM算法在凸优化问题上的效率优势[7]使得可以在不影响计算精度的前提下对稀疏成像过程并行加速,大大提升了计算性能。

考虑一般形式下具有等式约束的凸优化问题:

式中,x∈R n,A∈R m×n,f∶R n→R是凸函数,当目标函数f(·)可分离时即得到ADMM算法的一般形式,式(10)变为

则一般形式下的ADM M算法迭代步骤如下所示:

回归至稀疏成像领域的l1范数优化问题,式(10)中的函数f(·)对应为向量s的l1范数‖s‖1,优化模型变为

设h(·)是集合{s∈R n|As=y}的示性函数,则ADM M算法框架下的l1范数优化问题转化为

算法迭代步骤如下:

式中S1/ρ(·)为软阈值函数:

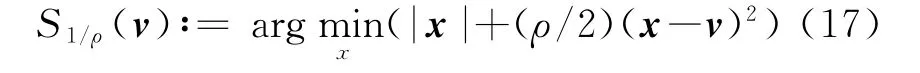
2.2 雷达成像模型

本文采用聚束雷达的工作模式,发射Bernoulli映射产生的混沌序列调频信号,假设目标的后向散射系数为各向同性,那么可以将雷达的回波模型写成:

式中,ξ(t)为高斯白噪声,λ为信号波长,Nt为场景中的目标个数,x(t)为发射信号,Ri(t)为第i个目标的瞬时斜矩:,v为载机速度,σi为第i个目标的回波幅度,c为光速。

要完成地铁噪声的主动消声控制，首先须对地铁噪声来源及其频谱特性进行深入分析.铁路噪声源主要包括线路噪声、站场噪声和工厂噪声三大部分，而我们所要分析和研究的为线路噪声.线路噪声属于流动污染源、具有线长、面广、间歇性等特点，由于其污染程度随列车速度的提高而日益加重，因此本文主要讨论铁路线路噪声的特点及其控制措施.普通铁路线路噪声的声源主要包含机车鸣笛噪声和轮轨噪声，以轮轨噪声为主，而对于提速后的城市轨道交通，其线路噪声还包括铁路桥梁结构的噪声、空气动力噪声以及集电系统噪声[9].

基于压缩感知理论的成像方式使得我们可以突破奈奎斯特采样定理的要求。假设目标场景的大小为M×N,在距离向和方位向对回波进行随机降采样得较小的K×L矩阵,这样得到的采样数据将远小于传统方法所需的数据量,然后利用压缩感知的方法重建大小为M×N的原始场景。

可以将目标场景的各列σi连接起来形成一个长度为M×N的列向量X:

同样将回波数据各列连起来组成一个长度为K×L的列向量Y:

则处理后的回波数据向量Y与场景列向量X的关系为

式中,N为加性高斯白噪声,Φ为KL×MN大小的矩阵,它的第i行第j列的元素为

根据所构建的观测矩阵Φ和降采样后的回波数据Y,可以借助上一小节所推导出的ADM M算法框架对原始场景进行重构。

3 实验与分析

本节主要通过仿真实验验证混沌序列调频信号应用于稀疏雷达的可行性。首先给出Bernoulli映射下的混沌序列调频信号波形,选定以概率密度函数ρ(x0)分布在区间[0,1]上的初值x0,通过式(3)迭代产生Bernoulli序列{xn},Bernoulli混沌序列长度为500,k取值3.7,信号带宽BW=150 M Hz,采样率为500 MHz,脉冲持续时间为20μs,最终得到的信号波形如图1所示。

图1 混沌序列调频信号波形

由图1可见,混沌序列调频信号具有类随机性,该特点使得其雷达波形难以辨识。为了验证信号的相关特性,选取信号的长度为相关长度,求得其自相关、互相关函数波形,如图2所示。

图2 混沌序列调频信号相关特性

然后给出一维稀疏场景下的仿真结果。信号为Bernoulli映射调制的混沌序列调频信号,带宽为150 MHz,脉冲持续时间为20μs,载频为1 GHz。所选场景中分布9个不同散射系数的目标点,如图3所示。

图3 原始观测场景

在回波信号中加入不同强度的加性高斯白噪声,观察不同信噪比和采样率下的一维成像结果。

从图4可以看出,在信噪比和采样率较高的条件下,利用压缩感知方法对回波数据进行处理可以较为完整地恢复原始场景信息,而相同条件下的时域相关法则由于自身的局限性在旁瓣水平和误差方面均劣于压缩感知处理方法。

在采样率保持一致的前提下,信噪比的降低将恶化各个目标重建的畸变程度;而相同信噪比条件下更低的采样率则可能导致目标重建位置的错误(如图中圆圈所示)。至于同样条件下的时域相关法(信噪比5 dB,采样率30%),其重建场景的旁瓣已淹没了主要目标的信息,无法重建原始场景。

为了更加直观地给出信噪比和采样率对稀疏重构算法的影响,图5给出了采样率分别为64%,50%和30%时,在不同信噪比条件下用蒙特卡洛方法画出的ADMM算法重构误差曲线。

接下来选取大小为30×30的二维场景进行仿真实验,场景中包含8个幅度随机的目标,如图6所示。

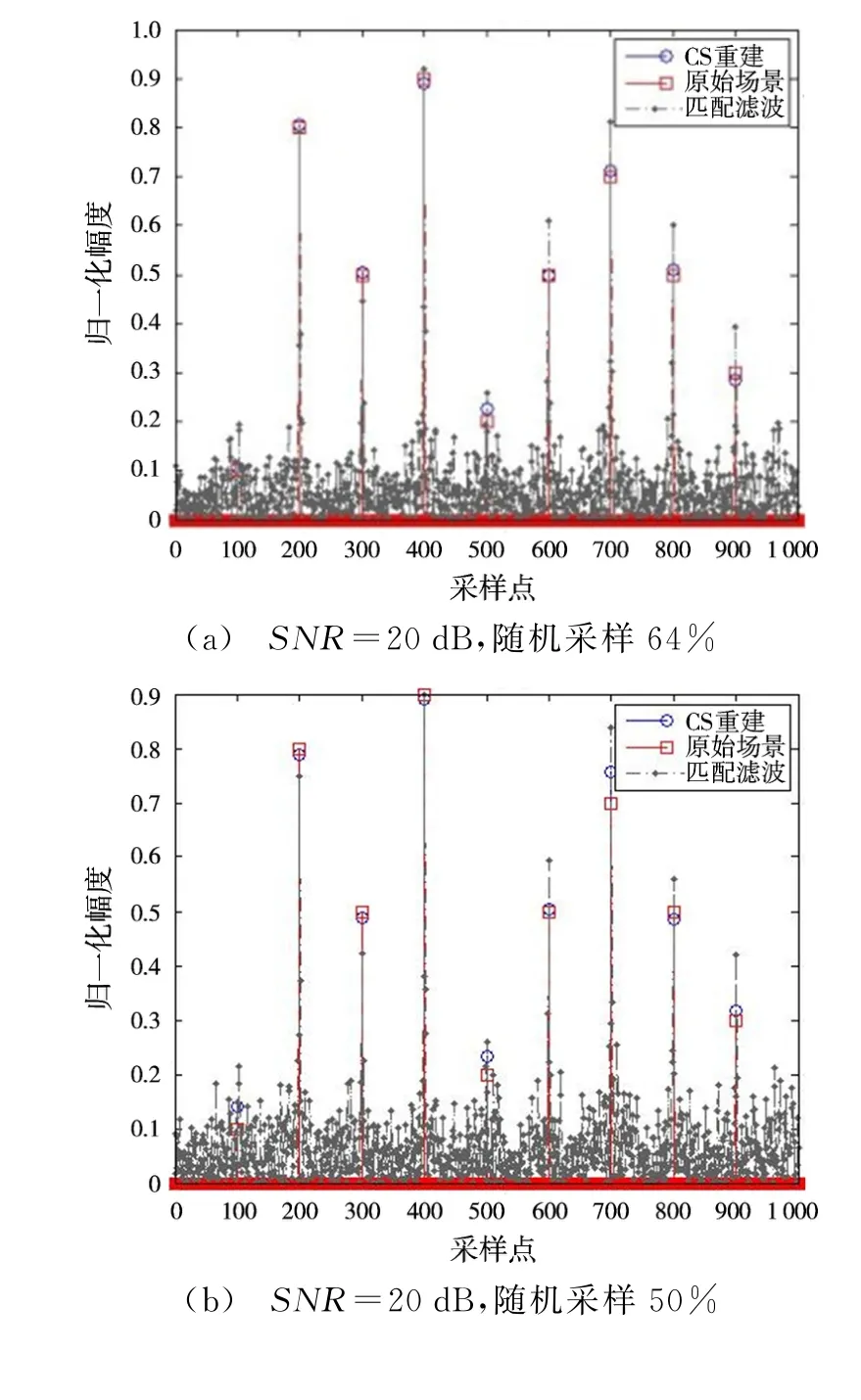
图4 不同采样率/信噪比条件下的一维仿真结果对比

图5 不同SNR下的重建误差曲线

图6 二维目标场景

发射信号为基于Bernoulli映射的混沌序列调频信号,带宽为150 MHz,脉冲持续时间为20μs,载频为1 GHz。仿真参数中斜距设为15 000 m,方位/距离向分辨率均为2 m,载机速度为150 m/s。在信噪比为20 dB和5 d B的条件下对回波信号进行64%(方位向80%、距离向80%)和30%(方位向50%、距离向60%)随机降采样后,基于ADMM方法的混沌调频信号稀疏雷达二维成像仿真如图7所示。

图7 不同采样率/信噪比条件下的二维仿真结果对比

可以看到在信噪比较高的时候,当采样率满足一定值时压缩感知方法能够准确重建目标场景,随着采样率的降低某些弱目标的重建会产生一定程度的畸变,但整体成像结果较为准确。信噪比的继续降低将恶化畸变现象,导致部分反射系数较弱的目标重建错误。

4 结束语

本文研究了基于混沌调频信号的稀疏雷达,建立了其成像模型。仿真实验证明混沌调频信号具有图钉形的模糊函数和类噪声特性,将其运用至稀疏成像雷达可以在降低信号采样率的前提下对原始场景进行准确重建,并且相比于时域相关成像法可以抑制图像的旁瓣。为了克服大目标场景下稀疏成像所带来的巨大计算量,ADMM算法能在不影响计算精度的前提下对稀疏成像过程并行加速,很好地为分布式稀疏重构提供新的思路。后续工作准备定量评价分布式ADMM算法相比于集中式稀疏算法所带来的时效性提升。

[1]DONOHO D L.Compressed Sensing[J].IEEE Trans on Information Theory,2006,52(4):1289-1306.

[2]杨广玉,马晓静,杨雪亚.基于时-空稀疏解的方位超分辨算法[J].雷达科学与技术,2014,12(2):171-175.

[3]ZHANG Bingchen,HONG Wen,WU Yirong.Sparse Microwave Imaging:Principles and Applications[J].Science China(Information Sciences),2012,55(8):1722-1754.

[4]BAYRAMI.On the Convergence of the Iterative Shrinkage/Thresholding Algorithm with a Weakly Convex Penalty[J].IEEE Trans on Signal Processing,2016,64(6):1597-1608.

[5]WANG J,KWON S,SHIM B.Generalized Orthogonal Matching Pursuit[J].IEEE Trans on Signal Processing,2012,60(12):6202-6216.

[6]BI Hui,ZHANG Bingchen,ZHU Xiaoxiang,et al.L1-Regularization-Based SAR Imaging and CFAR Detection via Complex Approximated Message Passing[J].IEEE Trans on Geoscience and Remote Sensing,2017,55(6):3426-3440.

[7]SUBRAMANIAN S,GANDHIRAJ R.Insight to AMP and ADMM Based Sparse Signal Reconstruction[C]∥International Conference on Communication and Signal Processing,Melmaruvathur,TN,India:IEEE,2016:1556-1559.

[8]雷超,胡进峰,刘立东,等.混沌二相码的性能分析[J].雷达科学与技术,2011,9(1):53-57.

[9]FLORES B C,SOLIS E A,THOMAS G,et al.Chaotic Signal for Wideband Radar Imaging[C]∥Proceedings of SPIE:Volume 4727,Orlando,FL,USA:SPIE,2002:100-106.

[10]DAWOOD M,NARAYANAN R M.Ambiguity Function of an Ultrawideband Random Noise Radar[C]∥IEEE Antennas and Propagation Society International Symposium,Salt Lake City,UT,USA:IEEE,2000:2142-2145.

[11]丁凯,杨汝良.混沌调频雷达成像仿真[J].电子与信息学报,2006,28(2):354-357.

[12]CANDÈS E J.The Restricted Isometry Property and Its Implications for Compressed Sensing[J].Comptes Rendus Mathematique,2008,346(9/10):589-592.

[13]BOYD S,PARIKH N,CHU E,et al.Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[J].Foundations and Trends®in Machine Learning,2011,3(1):1-122.