海杂波背景下的雷达性能评估研究

(南京电子技术研究所,江苏南京210013)

0 引言

雷达对海面上的目标进行探测时,会受到海表面对雷达发射信号后向散射的严重干扰,这些干扰通常称为海杂波。海杂波对雷达检测性能有严重影响,因此评估雷达在海杂波背景下的性能对雷达系统设计阶段有重大意义。

当前,复合K分布模型被广泛用作海杂波的幅度分布模型,然而即使在给出杂波模型的情况下,从纯粹的数学理论上评估雷达的检测性能依然存在很大的困难。尤其是涉及到杂波的相关性和目标的起伏特性时,雷达性能评估更加困难。在没有可供利用的、明晰的性能解析表达式之前,本文提出以仿真的K分布杂波为背景来评估雷达性能。另外,为了使仿真出的杂波逼近雷达的实际工作场景,建立雷达系统参数和环境参数与K分布模型的联系十分重要。因此,本文致力于解决“端到端”问题,即把雷达系统参数和环境参数作为输入,得出雷达的检测概率和虚警概率。

1 海杂波幅度分布模型

海杂波幅度分布模型的准确建立是进行雷达性能评估的重要前提。近几十年的研究表明[1-2],雷达在高分辨率、低擦地角情况下工作时,复合K分布模型可以很好地匹配海杂波的幅度分布特性。

复合K分布可以被看作是功率受一随机过程调制的瑞利随机变量,其中功率调制过程为Gamma分布。因此可以用两个独立随机变量(y与s)的乘积形式描述分布杂波幅度x的统计特性。其中,分量s称为散斑分量,用瑞利分布描述;分量y为功率调制分量,表征了杂波幅度局部均值水平,用Gamma分布来描述。

于是,复合K分布杂波对应的概率密度函数P(x)可以表示为

其中,散斑分量服从瑞利分布:

功率调制分量服从Gamma分布:

式中,v为形状参数,b为尺度参数,Γ(·)为伽马函数。〈y〉=v/b=Pc为海杂波平均功率。因此,K分布的概率密度函数表示为

式中,Kv(·)为v阶第二类修正贝塞尔函数。

2 参数模型

为了使仿真出的海杂波逼近雷达工作的实际场景,建立雷达参数和环境参数与K分布模型的联系很重要。而通过对复合K分布的描述可知,K分布模型完全由形状参数和尺度参数决定,所以建立雷达参数和环境参数与形状参数和尺度参数的联系就显得很有意义。

2.1 形状参数模型

2.1.1 模型1

Ward[3]通过对机载雷达试验数据进行分析建立了一个形状参数的经验模型。推断该模型的数据来自于一部距离分辨率为4.2 m的雷达,其工作于I波段(9～10 GHz),但据信该经验模型在5～35 GHz范围内可以很好地应用。其表达式为

式中,入射余角φgr的范围为0.1°＜φgr＜10°,kpol为与极化方式相关的参数(HH极化为2.09,VV极化为1.39),θsw为相对于浪涌方向的姿态角(若没有涌浪,最后一项则可忽略),Ac为雷达分辨单元面积,其值为

式中,θaz为天线方位波束宽度,φgr为入射余角,距离分辨率,ρ=c/(2B),B为带宽,因子α用于表征方位和仰角波束形状的影响,本文令α的值为0.753。

2.1.2 模型2

Watts和Wicks[4]用距离分辨率同为4.2 m的雷达采集了更多数据,并将这些数据和模型1所用的数据整合到一起。他们利用水平和垂直极化数据分别在逆/顺着涌浪方向和垂直于涌浪方向上进行拟合,得到v的经验模型为

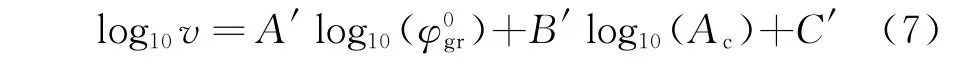
A′,B′和C′的值由表1给出。

表1 A′,B′和C′的参数值

对比两个模型可以发现,在相同的入射余角和横向距离分辨率的情况下,模型2对应的v值分布范围比模型1的大。然而模型2只能估计逆/顺着涌浪方向和垂直于涌浪方向的v,不能估计其他方向的v。此外,模型2的均方根误差也比模型1的大。

2.2 尺度参数模型

K分布模型尺度参数b的计算公式为

式中,Pc为海杂波平均功率,其表达式为

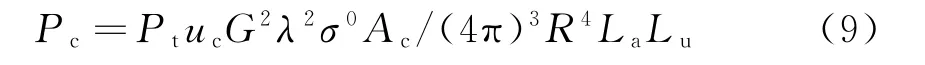
式中,Pt为雷达发射机功率,uc为脉冲压缩增益,G为天线增益,λ为雷达波长,Ac为海面被照射的面积,R为雷达作用距离,La为由于大气和所有气象现象的吸收作用导致的传播损耗,Lu为雷达损耗,σ0为海杂波NRCS,其值由下一小节给出。

2.3 归一化海杂波RCS模型

归一化海杂波RCS的研究是一个重要问题,由于微波频率的海洋散射机理非常复杂,运用现有的海洋散射理论知识还不足以准确地预估海面平均反射系数(NRCS)。因此,研究者结合其他的分析方法,开发了几个预估RCS的半经验模型。这些半经验模型主要有GIT模型、TSC模型、HYB模型和NRL模型。本文给出GIT模型的具体表达式。

2.3.1 GIT模型

GIT模型[5]是乔治亚理工学院的工作人员提出的模型。这个模型适于1～100 GHz雷达频率范围和0.1°～10°入射余角范围,覆盖了从顺风到逆风的所有方向。该模型建立在一种隐含的多路径模型以及从试验数据集合中观测到的更一般趋势的基础之上。鉴于经常用到的雷达频率范围,本文给出1～10 GHz时NRCS的计算公式:

式中,λ为雷达波长(m),φgr为入射余角(rad),hav为平均浪高,Ai=σ4φ/(1+σ4φ)为多径或干涉参数,其中σφ为粗糙度参数:

式中,hav=0.004 52U2.5为平均浪高,U为风速,可根据海况S得到

风向相关性Au为

式中,θw为风向与雷达观察方向的夹角。风速因子Aw为

2.3.2 TSC模型

TSC模型是依据对Nathanson的数据进行拟合得到的,该模型在形式上与GIT模型类似,但又有些不同。尤其是TSC模型包含了异常传播情况下采集的数据,而GIT模型不包含这些数据。这导致TSC模型的NRCS不会像GIT模型那样随着入射余角的减少而快速减少。TSC模型频率适用范围是0.5～35 GHz,入射余角适用范围是0°～90°。跟GIT模型一样,该模型也覆盖了从顺风到逆风的所有方向。当传播环境未知时,采用TSC模型比GIT和SIT模型更好,因为TSC模型更接近所有传播环境的平均。该模型的具体形式见文献[6]。

2.3.3 HYB模型和NRL模型

HYB模型是Reilly和Dockery综合Nathanson数据和GIT模型的特点而提出的混合模型,该模型的入射余角覆盖范围为0.1°～30°,频率覆盖范围为0.5～35 GHz,该模型的具体形式见文献[7]。

NRL模型是Gregers-Hansen和Mital提出的新模型[8],该模型仅适用于侧风情况,频率覆盖范围为0.5～35 GHz,入射余角覆盖范围为0.1°～10°,其具体形式见文献[8]。文献[9]指出,与以上3种模型相比,在相同因素下NRL模型与实测海杂波数据最吻合,如果只评估侧风情况下的NRCS,可率先考虑NRL模型。

表2给出了各种模型的适用条件,在一组给定的雷达参数和应用环境下,用上文给出的4种模型所获得的NRCS值可能不一样,实际情况也是如此,因为真实的海况本来就难以描述。这些模型的价值在于它们在雷达系统设计中的应用,它们可以给雷达设计者提供一个非常好的NRCS取值范围。针对具体的环境因素,雷达设计者可以选择合适的估计模型。

表2 模型适用范围对比

3 杂波仿真

海杂波的精确仿真关乎到雷达性能评估的准确性,文献[10-14]研究了海杂波的仿真。本文采用SIRP法仿真出时空相关的海杂波,其时间相关性和空间相关性的具体描述可参考文献[12]。仿真原理如图1所示。

图1 K分布杂波仿真原理图

仿真步骤:

1)根据杂波的时间相关函数确定相关杂波的协方差矩阵M,通过Cholesky分解得矩阵A,其中M=AAT,产生复高斯白噪声W1,然后通过线性变换得X=A W1;

2)产生白高斯序列W2(n),由参数模型获得形状参数v和尺度参数b,同时确定杂波的空间相关性,根据v和b以及杂波的空间相关性作相关性处理得相关伽马分布序列Z(n),文献[10]给出了其相关性处理过程;

3)对相关伽马分布序列取算术平方根得到序列S(n),将S(n)纵向展开得到矩阵S(m,n);

4)矩阵X和矩阵S对应元素相乘得Y,即为所需的时空相关二维杂波矩阵。

4 雷达性能评估

为了评估雷达性能,需要估计雷达接收机匹配滤波器输出端的平均信号、杂波和噪声功率(Ps,Pc,Pn):

式中,σt为目标的平均RCS,k为玻耳兹曼常数(k=1.38×10-23),T0=290 K为环境参考温度,B为带宽,Fn为噪声系数。Pc由式(9)给出。

从数学理论上计算雷达的检测概率存在很大困难,本文给出如图2所示方法来评估雷达性能,步骤如下:

1)设定雷达系统参数和雷达工作环境参数;

2)根据设定的应用环境,选择合适的NRCS模型和形状参数模型,分别计算出σ0和v;

3)根据式(9)计算出海杂波的平均功率Pc,并计算尺度参数b;

4)由式(20)和式(21)分别计算出目标信号平均功率Ps和噪声平均功率Pn;

5)根据获得的v和b及其杂波的时间相关性和空间性对K分布杂波进行仿真;

6)根据Pn对热噪声进行仿真;

7)选定目标类型(Swerling 0/1/2/3/4),根据Pc对目标信号进行仿真;

8)将5)～7)仿真获得的序列进行简单的叠加,并以此为背景,选定CFAR类型同时结合蒙特卡洛法评估雷达性能。

5 实验结果

依照本文讨论的雷达性能评估方法进行仿真实验,为了简单,本文只进行了单脉冲检测评估。设定初始参数如表3所示,空间相关性符合指数相关,时间相关性对应的功率谱密度为高斯谱。NRCS模型选择GIT模型,形状参数估计选择模型1,CFAR检测选择CA-CFAR。设定CFAR参考单元为32个,保护单位为2个,蒙特卡洛仿真次数为107次。

图2 雷达性能评估体系

表3 仿真参数

仿真结果如图3、图4所示,图3为仿真产生的相关K分布杂波序列,与理论拟合得很好,验证了仿真的正确性;图4给出了雷达对Swerling 0型和Swerling 2型目标的检测概率与CFAR门限系数的关系,结果表明目标的起伏特性对雷达的检测性能有很大影响,目标的起伏会降低雷达的检测概率。

图3 某时刻距离维杂波幅度和概率密度

图4 不同类型目标的检测概率与门限系数的关系

改变初始参数里的某个变量,结果如图5～图7所示。图5表明雷达在顺风、逆风和侧风观测时雷达虚警概率相差无几。图6显示相对于逆着浪涌和顺着浪涌,雷达垂直浪涌方向观测时会有更低的虚警概率。这是因为有浪涌存在时,雷达逆着或顺着浪涌方向观察时杂波最为尖锐,说明雷达在垂直浪涌方向工作时会得到更好的性能。图7给出了雷达在不同海况下的检测性能,对比可知,海况等级越高雷达的检测性能越差。

最后,比较CA-CFAR和OS-CFAR检测性能间的差异。CA-CFAR和OS-CFAR参考单元都是32个,保护单元都为2个,OS-CFAR以第24个单元的幅度作为估计幅值。其结果如图8所示,由图可知在同样的检测概率情况下,CA-CFAR的虚警概率更低,表明相对于OS-CFAR用CA-CFAR检测目标会得到更好的性能。

图5 不同风向的虚警概率与门限系数的关系

图6 不同浪涌方向的虚警概率与门限系数的关系

图7 不同海况的检测性能

图8 不同CFAR的检测性能

6 结束语

本文建立了雷达在实际工作环境下的性能评估体系,以雷达系统参数和环境参数作为输入,最终得出雷达的检测概率和虚警概率,对雷达系统工程师具有较好的实用价值。当然本文也存在一些不足之处,为了使雷达性能评估更加准确,还应建立杂波相关性与雷达参数和环境参数的联系,这也是本文今后努力的方向。

[1]丁昊,董云龙,刘宁波,等.海杂波特性认知研究进展与展望[J].雷达学报,2016,5(5):499-516.

[2]SCHOENECKER S,WILLETT P,BAR-SHALOM Y.The Effect of K-Distributed Clutter on Trackability[J].IEEE Trans on Signal Processing,2016,64(2):475-484.

[3]WARD K D.Compound Representation of High Resolution Sea Clutter[J].Electronics Letters,1981,17(16):561-563.

[4]WATTS S,WICKS D C.Empirical Models for Detection Prediction in K-Distribution Radar Sea Clutter[C]∥IEEE International Conference on Radar,Arlington,VA:IEEE,1990:189-194.

[5]HORST M,DYER F,TULEY M.Radar Sea Clutter Model[C]∥IEEE International Conference on Antennas and Propagation,London:IEEE,1978:6-10.

[6]ANTIPOV I.Simulation of Sea Clutter Returns[R].Salisubry:Defence Science and Technology Organisation,1998.

[7]REILLY J P,DOCKERY G D.Influence of Evaporation Ducts on Radar Sea Return[J].IEE Proceedings F:Radar and Signal Processing,1990,137(2):80-88.

[8]GREGERS-HANSEN V,MITAL R.An Improved Empirical Model for Radar Sea Clutter Reflectivity[J].IEEE Trans on Aerospace and Electronic Systems,2012,48(4):3512-3524.

[9]任红霞.雷达海杂波统计建模与仿真[D].青岛:中国海洋大学,2015.

[10]曹艳霞,李国君.基于K分布舰载雷达海杂波仿真方法研究[J].雷达科学与技术,2016,14(1):86-90.CAO Yanxia,LI Guojun.Study on Simulation Method of Ship-Borne Radar Sea Clutter Based on K Distribution[J].Radar Science and Technology,2016,14(1):86-90.(in Chinese)

[11]VAN DER MERWE J R,STRYDOM J J,CILLIERS J E.Realtime Generation of K-Distributed Sea Clutter for Hardware in the Loop Radar Evaluation[C]∥2016 European Radar Conference,London:IEEE,2016:17-20.

[12]赵海云,胡学成.时空二维相关K分布雷达海杂波建模与仿真[J].中国电子科学研究院学报,2008,3(5):515-519.

[13]谭龙,陈秋菊,吴惟诚,等.远程预警雷达海杂波信号仿真[J].电子信息对抗技术,2016,31(4):79-82.TAN Long,CHEN Qiuju,WU Weicheng,et al.The Simulation of the Sea Clutter for Long-Distance Early-Warning Radar[J].Electronic Information Warfare Technology,2016,31(4):79-82.(in Chinese)

[14]高鑫,苟川杰,张磊,等.相参海杂波建模与建模和仿真研究[J].船电技术,2016,36(7):24-27.