平面近场测试高斯波束束腰半径的方法
陈 谦,金谋平,汪 伟,李 佩,2
(1.中国电子科技集团公司第三十八研究所,安徽合肥230088;2.孔径阵列与空间探测安徽省重点实验室,安徽合肥230088)
0 引言
毫米波波束波导、反射面天线等准光学器件装置在深空探测、气象测量和卫星遥感等领域得到广泛应用[1-3]。毫米波准光学器件装置的出射波束近似高斯分布,可利用高斯波束理论来指导器件装置设计、加工、安装、测试。束腰半径作为高斯波束最重要的参数,其测试十分关键。毫米波准光学频段波长很短,对测试装置、设备精度要求很高。据报道,测试束腰半径的方法主要有扫描狭缝法[4-5]、刀片边缘法[6-7]及针孔法[8]等。通常,这些方法需要利用透镜将出射波束进行聚焦,然后在小范围内扫描场强或功率分布计算得出束腰半径。这些测试方法需要搭建波束束腰半径专门测试平台,需要多种测试器件装置及操控仪器仪表,且主要用于激光类小尺寸装置束腰半径的测试。对于大尺寸、宽出射波束装置的测试,上述测试平台难以达到测试条件要求。
本文提出了一种利用平面近场测试高斯波束束腰半径的方法,可满足大口径器件、装置的测试。而且,此测试方法完全借助平面近场测试设备,无需额外配置其他辅助装置,通用性好。
1 束腰半径测试原理
本测试方法主要借助平面近场测试获得毫米波准光学器件装置高斯波束近场扫描数据,利用近场数据反演、高斯函数拟合及高斯波束传输理论计算获得束腰半径大小及位置。
利用平面近场测试设备完成毫米波准光学器件装置出射波束的近场扫描,记录近场扫描数据,利用近场测试数据反演,得到出射波束远场方向图。根据远场方向图数据,提取3~5个不同锥削电平下的锥削角度,并根据式(1)计算出射波束束腰半径大小w0。

选取多个锥削电平及其对应的锥削角度来计算多组束腰半径值,对这些束腰半径值求平均作为装置的束腰半径大小。采用多组数据取平均值可消除单组数据计算带来的偏差。在工程应用中,-10 d B锥削电平及其对应的锥削角度是常用参照数值。
由于近场采集的数据分布跟理想高斯波束近场数据分布存在差异,通过高斯函数拟合能修正近场采集数据的随机误差。采用高斯函数拟合近场记录的电场幅度随扫描步长的曲线,根据拟合曲线计算近场分布对应的波束半径大小,此波束半径为测试探头处的波束半径。拟合用的高斯函数为

式中,y0,v,xc,B均为拟合参数。
根据拟合曲线,确定高斯拟合曲线峰值,峰值下降1/e对应两个点,设为M,N。M,N两点间距即为2倍的波束半径值,等于两点扫描步数差与扫描步长的乘积。分别拟合垂直向和水平向的近场电场幅度随扫描距离的分布曲线,即可得到垂直向和水平向的波束半径大小,分别设为wv和wh。
根据高斯波束传输理论,已知w0v,w0h,wv,wh即可计算出束腰半径距离扫描探头处的距离,定义垂直向和水平向束腰半径位置分别为zv和zh。则

根据zv,zh即可确定束腰半径的位置。理想高斯波束w0v和w0h相等,wv和wh也相等。通常,测试的出射波束只是准高斯波束,所以垂直向和水平向的束腰半径存在差异。可将w0v和w0h的平均值作为毫米波、准光学装置的束腰半径值,zv,zh的平均值作为束腰半径位置的确定值。
2 测试实例分析
前期研究中,本课题组设计了一种W波段双极化收发分离的波束波导馈电网络[9]。在此,选取该波束波导馈电网络一个工作通道的出射波束作为实例用以说明束腰半径测试方法。该通道出射波束近场测试如图1所示。探头水平向和垂直向扫描步长为1 mm,扫描步数均为61步,测试频率为94.05 GHz。

图1 波束波导近场测试示意图
近场测试结果如图2所示,可见该波束波导出射波束基本满足高斯波束分布。对近场数据反演处理得到波束波导远场方向图,如图3所示。-10 d B锥削电平对应的锥削角度是波束波导设计常用的指标参数,采用式(1)计算了-8 dB,-10 d B,-12 dB锥削电平下的束腰半径大小,如表1所示。对计算的3组数据求平均,平均值作为束腰半径大小。由此得到水平向束腰半径w0h=2.261 mm,垂直向束腰半径w0v=2.443 mm。
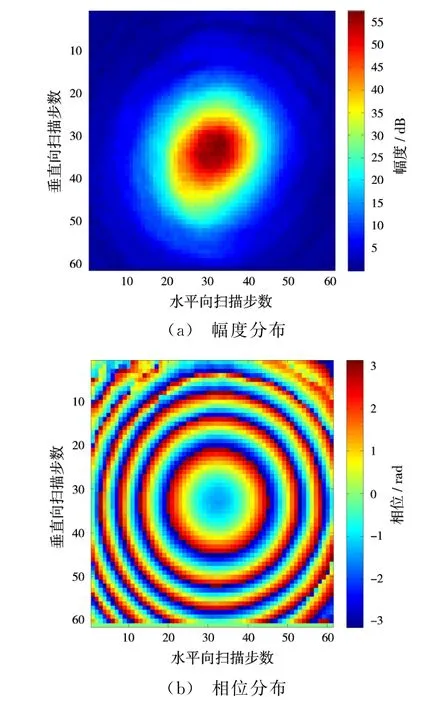
图2 近场幅度相位分布图

图3 波束波导出射方向图
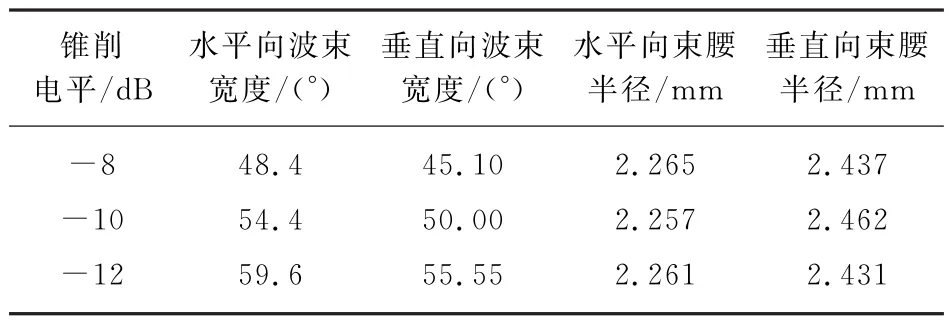
表1 垂直向和水平向不同锥削电平下的波束宽度
因波束波导出射波束近场分布只是近似满足高斯分布,直接按定义计算波束半径随机误差太大,难以代表出射波束的特性,对近场测试数据进行高斯函数拟合,根据拟合曲线计算波束半径可较好地体现整个出射波束特性。选取垂直向和水平向近场采集数据进行高斯函数拟合,拟合曲线如图4所示。

图4 近场幅度分布高斯函数拟合
根据拟合曲线,计算得到探头处水平向、垂直向波束半径wh=13.275 mm,wv=14.56 mm。进一步,借助式(3)计算出波束束腰半径距离探头处的距离,zh=29.15 mm,zv=34.56 mm。zh和zv的平均值作为束腰半径距离探头的距离,在已知探头位置情况下,即可确定束腰半径的具体位置。
图2(a)中,波束波导出射波束近场电场强度分布所形成的光斑呈椭圆形,水平向窄,垂直向宽,这说明水平向束腰半径要小于垂直向束腰半径。实际测试得出的水平向束腰半径值小于垂直向束腰半径值,符合上述判断结论。
4 结束语
本文提出了一种利用平面近场测试高斯波束束腰半径的方法,并结合具体波束波导馈电网络测试案例论述了此方法的可行性。该测试方法完全借助平面近场测试条件,无需额外添加其他测试设备,无需额外搭建测试平台,具有很好的实用性、适应性。本方法可用于指导毫米波准光学器件的设计及级联安装调试,具有较高工程价值。
[1]钱军,牛忠文.机载毫米波测云雷达吊舱关键技术研究[J].雷达科学与技术,2014,12(2):206-209.
[2]苏涛,高仲辉,黄兴玉.94 GHz机载测云雷达总体技术研究[J].雷达科学与技术,2013,11(6):574-577.
[3]冯永会,王金虎,葛俊祥.毫米波测云雷达回波的衰减订正研究[J].微波学报,2016,32(5):89-96.
[4]WRIGHT D,GREVE P,FLEISCHER J,et al.Laser Beam Width,Divergence and Beam Propagation Factor:An International Standardization Approach[J].Optical and Quantum Electronics,1992,24(9):993-1000.
[5]MCCALLY R L.Measurement of Gaussian Beam Parameters[J].Applied Optics,1984,23(14):2227.
[6]ARNAUD J A,HUBBARD W M,MANDEVILLE G D,et al.Technique for Fast Measurement of Gaussian Laser Beam Parameters[J].Applied Optics,1971,10(12):2775-2776.
[7]SUZAKI Y,TACHIBANA A.Measurement of the μm Sized Radius of Gaussian Laser Beam Using the Scanning Knife-Edge[J].Applied Optics,1975,14(12):2809-2810.
[8]SHAYLER PJ.Laser Beam Distribution in the Focal Region[J].Applied Optics,1978,17(17):2673-2674.
[9]陈谦,梁冰苑,方正新,等.一种双极化收发分离的波束波导馈电网络[J].雷达科学与技术,2016,14(5):549-553,557.

