几何画板辅助初中几何教学的思考

【摘要】新时期下，伴随着我国信息技术的快速发展，越来越多的现代化教学方法被应用在初中数学教学活动中，这也极大的提升了课堂教学效率。对于初中几何教学，其具有很强的抽象性，对学生空间思维要求比较高，使得学生会感觉学习几何知识十分困难。几何画板是一种现代化的教学辅助手段，将其应用在初中几何教学中，可以极大提升学生思维，促使学生更加主动探究几何知识，下面对此进行分析。

【关键词】几何画板  初中  几何教学

【中图分类号】G633.6;G434 【文献标识码】A 【文章编号】2095-3089（2018）43-0147-01

前言

对于几何画板是一种现代化教学辅助工具，可以将抽象的数学知识变得形象化、具体化，特别是其动态演示功能，可以带给学生直观、立体、动态的感受，极大的增强了学生的学习兴趣，同时也為初中几何教学提供了良好的教学手段。为了充分显示几何画板在初中几何教学中的优势，本文以结合一道典型的几何题为切入点展开分析。

如下图1所示，在正方形ABCD中，点P处于BC边上，但不与B、C点重合，连接AP，并平移△ABP，使得B点移动至C点，得出△DCQ，作QH⊥BD与H点，连接AH、PH，求AH与PH关系，并证明。

1.用多方法培养学生思维发散能力

在以上题目中，证明AH与PH关系的方法有很多，为了帮助学生可以从多角度认识图形的关系，教师可以利用几何画板辅助教学，一是填充全等三角形，寻找更多的条件;二是通过几何画板的动画演示，实现图形翻折、旋转等，实现图形的动态展示，让学生更好的探究图形内在关联。

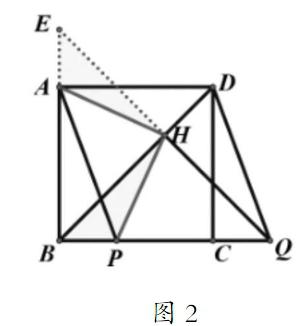
在这个题目中，给出条件正方形ABCD，那么其隐藏的条件就是BD是正方形ABCD的角平分线，这时就可以通过角平分线构造全等三角形，构造出和△BPH全等的三角形，如下图2所示，通过正方形轴对称性，沿着BD对△BHQ进行翻折，得到△BHE，这时，学生只需要证明了△AHE≌△PHB，就可以证明AH⊥PH。

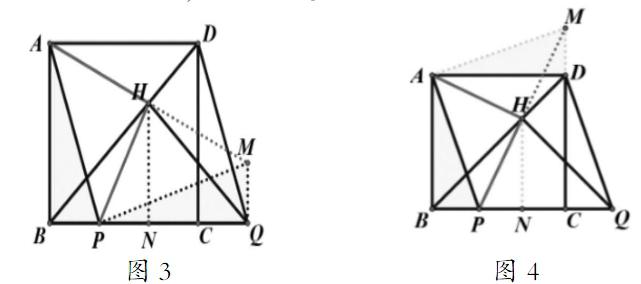
在证明AH=PH且AH⊥PH时，由于无法证明△AHP是等腰直角三角形，因此，可以从证明AH、PH是等腰直角三角形斜边上的中线进行。对此，有两种方法进行：（1）如下图3所示，过Q点，作BQ的垂线，与AH的延长线相较于点M，连接PM，然后展开证明。（2）从结论出发，利用等腰直角三角形的相关知识展开分析，通过几何画板动态展示延长线的形成过程，并过定点做出已知直线的垂线，构造所需的全等三角形，如下图4所示，进行证明。

学生在解题过程中，教师可以利用几何画板进行动态演示，让学生在图形的旋转、翻折等过程中，可以更好的理解、感悟图形的关系，掌握图形的生成过程，促使学生更好的学习几何知识。

2.利用动点问题进行深入探究

在初中几何教学中，利用几何画板的动画功能，可以将运动效果生动、连续的表现出来，使得学生可以意识到运动轨迹是动态的、逐步形成的，学生在观察几何画板中的运动轨迹时，会通过观察、实验、猜测、推理、证实、交流等活动，加深自身对几何知识的认识，这对于学生更加积极的参与到初中几何学习中有极大的帮助。同时在几何画板中，教师还可以引导学生通过一些按钮、动画来实现从特殊图形向一般图形进行研究的思想，如在上题中，教师可以将P点移动至B点，让学生分析这种特殊情况下的结论，或者将P点拖动到BC、CB的延长线上，通过改变图形样式，让学生学会从特殊到一般的研究思想。在初中几何教学中，利用几何画板可以极大的提升课堂教学实效性，并且能引导学生更加直观的观察图形本质。

总结

综上所述，在初中几何教学中，通过几何画板可以极大的调动学生的学习主动性，并引导学生从多角度、多思维进行问题思考，这对于学生的健康发展有极大的帮助。因此，在实际中，初中数学教师要结合学生的具体情况，合理的应用几何画板辅助教学，以此加深学生对于几何知识的认知。

参考文献：

[1]谭敏.几何画板辅助初中数学教学的思考[J].读书文摘，2017（7）：141-142.

作者简介：

郑汉森（1974.05.02-），男，汉族，黑龙江省哈尔滨市人，本科，一级教师，研究方向：数学。