双小行星系统引力场建模方法研究

步士超，王宇凯,2，李文丹，李爽，牛升达

（1. 南京航空航天大学 航天新技术实验室，南京 210016；2. 上海微小卫星工程中心，上海 201210；3. 上海卫星工程研究所，上海 201109）

0 引 言

小行星因其包含了太阳系起源、行星演化等方面的重要信息，以及其可能蕴藏的丰富矿藏资源和潜在的对地球撞击的威胁，已经成为21世纪国际深空探测活动的重点目标。随着我国深空探测持续不断向前推进，开展对具有独特科学价值的小行星的探测已经成为深空探测技术发展的必然趋势。双小行星系统是众多小行星类群中的一种特殊形式，是指两颗小行星围绕其共同的质心旋转，同时两者的质心围绕太阳做公转运动。研究表明双小行星系统是太阳系中十分普遍的物理现象，大约有16%的近地小行星和主带小行星属于双小行星系统[1]。对两颗小行星构成的双小行星系统进行探测具有多种探测单颗小行星所不具备地独特科学价值，例如，许多双小行星系统是由单颗小行星分裂而演化导致，于是，原本隐藏于小行星内部的深层结构便由于分裂而直观地展现在分裂后的双小行星系统的表面上，通过对这种结构的直观分析，可以获得对小行星结构构造、动力学特性等方面的更深层洞见。

双小行星系统引力场与动力学建模是进行弱引力双小行星系统探测任务设计时首先需要解决的问题，更是研究双小行星系统附近的飞行器轨道动力学特性和相关任务轨道设计的基础。

因此，本文拟采用不同的引力场简化模型，针对弱引力双小行星系统的引力场进行建模，对双小行星系统动力学特性进行较全面的研究分析，为我国正在论证中的小行星采样返回探测任务提供一定的技术支持。

1 限制性全三体问题

1996年以前，针对形状不规则的小行星的引力场建模问题，学者们一般将其近似为三轴椭球体；1996年以后，多面体模型法在小行星的引力场建模中得到了广泛的应用，从而使人们能更精确地研究小行星附近的航天器轨道动力学问题。例如，Scheeres和Hudson等分别以形状不规则的小行星4769 Castalia以及4179 Toutatis为例研究了其附近的轨道动力学问题[2-3]，详细地分析了其重力场的特征情况、近小行星轨道动力学方程等方面的问题。在2005年后，D. J. Scheeres等学者针对双小行星系统附近的航天器运动的轨道动力学问题等开展了研究与分析[4-6]，深入分析了航天器在双小行星系统中的轨道特点，并且研究了小行星系统三体问题中小天体的非球形摄动对轨道的影响。

但是，双小行星系统附近的探测器动力学建模问题比较复杂，如果把两个小行星的不规则引力场和自旋转等因素都考虑进去就是非常复杂的全三体问题，如图1所示，全三体问题到目前为止基本上处于无解状态。北京理工大学的李翔宇和乔栋等针对1996FG3双小行星系统，采用双球体模型，对逃逸轨道展开了设计[7]，如图2所示。但是，双球体模型相对于实际的双小行星系统的误差比较大。Bellerose和Scheeres将双小行星系统其中一个天体的质量分布引入考虑，以均匀三轴椭球体和球体分别来近似两个天体，构成限制性全三体问题（椭球体–球体模型），如图3所示，并分析了双小行星系统中航天器的运动规律，如平动点、雅可比常数、周期轨道稳定区域、双星间转移轨道等等[4,8-9]。

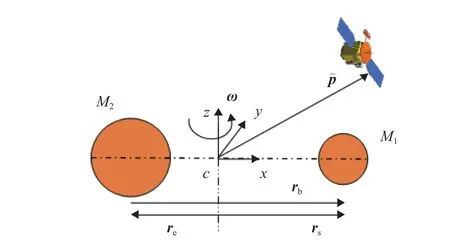
图2 球体–球体模型示意图Fig. 2 Schematic diagram of the sphere-sphere model

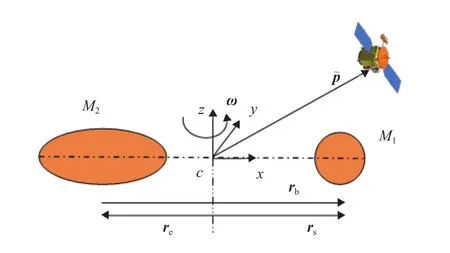
图3 椭球体–球体模型示意图Fig. 3 Schematic diagram of the ellipsoid-sphere model

1.1 采用椭圆积分计算的椭球体-球体模型

首先，我们以Bellerose和Scheeres提出的一个简化的双小行星系统椭球体–球体模型为例（图3）[8-9]。考虑一个质点或航天器在双小行星系统的引力场范围内。M1为球体的质量，M2为椭球体的质量，rb为球体相对于椭球体的位置矢量，re为椭球体相对于系统质心CM的位置矢量，rs为球体相对于系统质心CM的位置矢量，为航天器相对于质心CM的位置矢量。

假设航天器（或质点）对双小行星系统的运动没有影响，那么航天器的运动方程为

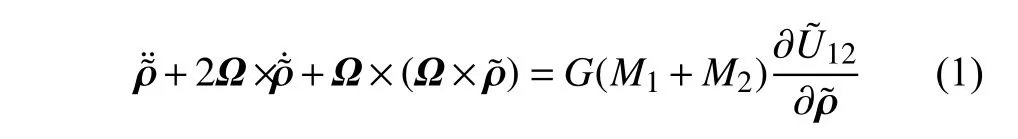
设椭球体最长轴的半长轴为α，那么在此半径下，系统平均角速度为在这里，我们以α和n为标准作为归一化的长度和角速度单位，那因此方程（1）归一化后，变为

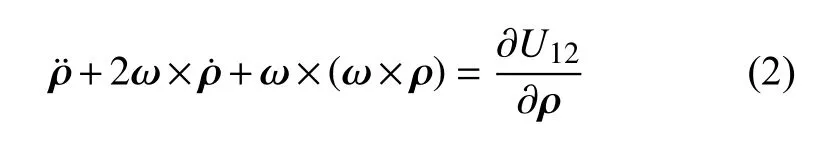
其中

式（3）是在如图3所示的长轴稳定结构下ω的取值情况所得。

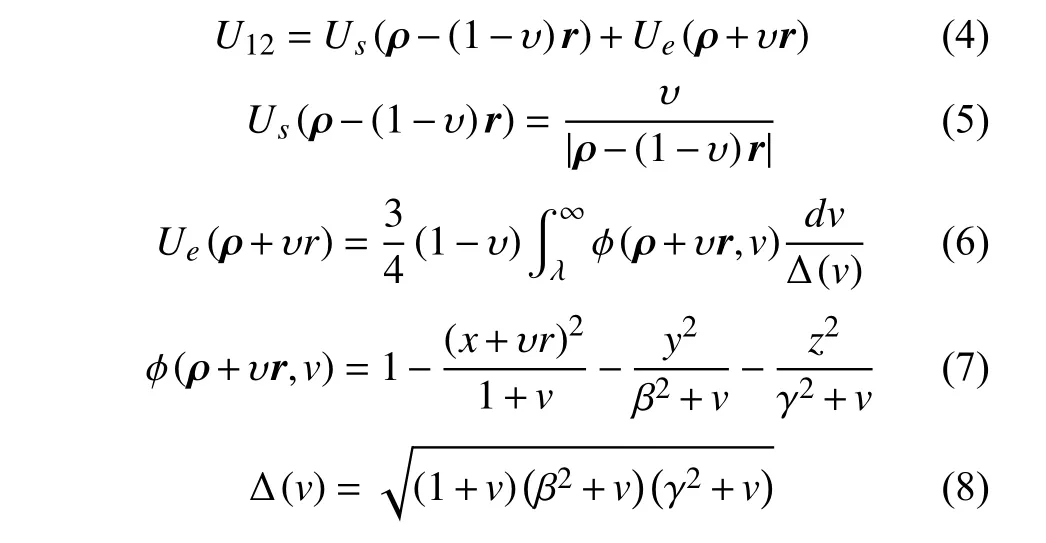
1.2 采用椭圆积分计算的椭球体–椭球体模型

在前文的椭球体–球体模型的基础上，本节提出了一种改进的限制性椭球体–椭球体模型，如图4所示。限制性椭球体–椭球体模型本质上是将“椭球体–球体模型”中的“球体”替换为一个“限制性椭球体”，即将图3中的球体M1改进为一个限制性椭球体，将其三轴改为并且使用椭圆积分来计算其引力势能，以便使更新后的双小行星系统引力场模型能更准确地描述探测器近双小行星系统动力学问题。

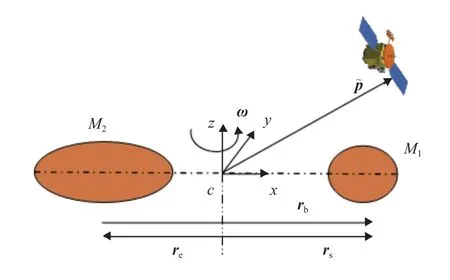
图4 限制性椭球体–椭球体模型示意图Fig. 4 Schematic diagram of the restrictive ellipsoid-ellipsoid model

在此限制性椭球体–椭球体模型下

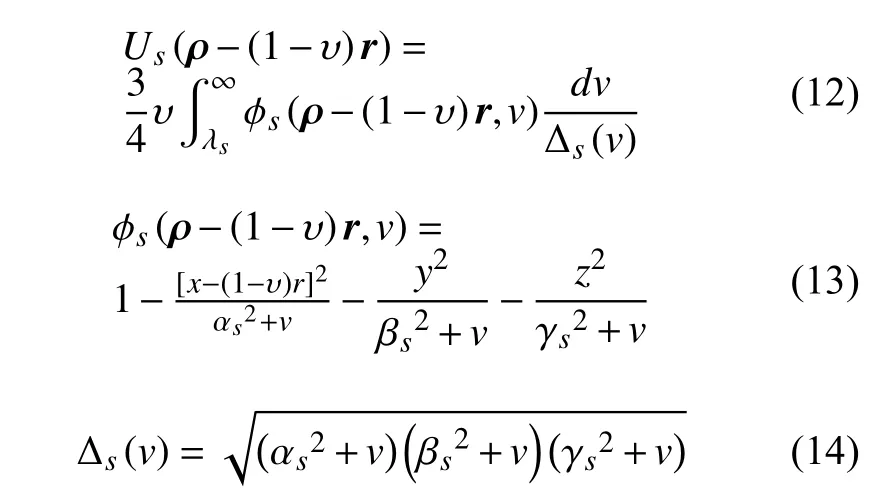
2 采用二阶二次球谐函数模型的双小行星系统引力场建模

在1996年，Kaula等学者建立了球谐函数模型理论[10]，其使用一系列的球谐函数展开式来逼近小行星的引力场。球谐函数模型具有计算效率高、有明确解析表达式和各阶摄动大小明显等优点，因此其广泛地应用于天体力学和人造航天器轨道动力学等方面。在前文中，都是采用椭圆积分来计算各种模型中的引力势。但是，在计算过程中过多地引入积分计算环节，会大大地增大计算量和计算难度，消耗更多的计算时间。因此，在本节中，采用计算效率高，无积分环节的二阶二次球谐函数模型来进行双小行星系统的引力场建模[11]。

小行星的引力势函数可由球谐函数展开式来逼近，如下式所示

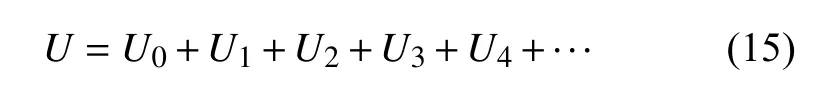
胡维多等学者[11-12]研究发现采用二阶二次球谐函数模型来计算小行星引力场既能得到比较精确的结果，还能兼顾计算的简便程度。在本节中，忽略球谐函数模型的高阶项，取二阶二次球谐函数模型，因此小行星引力势为

其中：δ为纬度；λ为经度。

当以中心引力体的质心作为坐标系的原点时，那么二阶二次球谐函数模型中的参数取值为而当该中心引力体固连坐标系的三轴沿着中心体的主惯量轴方向时，那么参数因此，在这种坐标系下，利用二阶二次球谐函数模型计算的天体引力场可以简化为

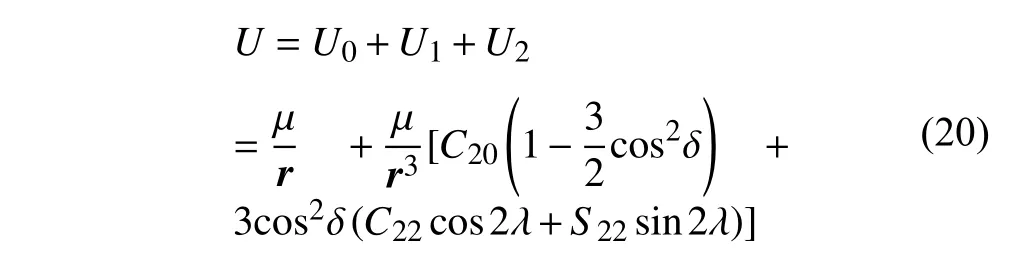
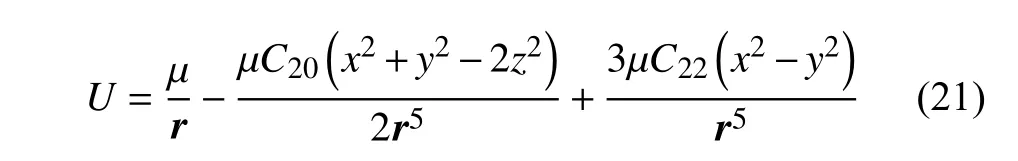
其中，两个系数C20和C22与中心引力体的3个主惯量轴的转动惯量有如下关系[11-12]

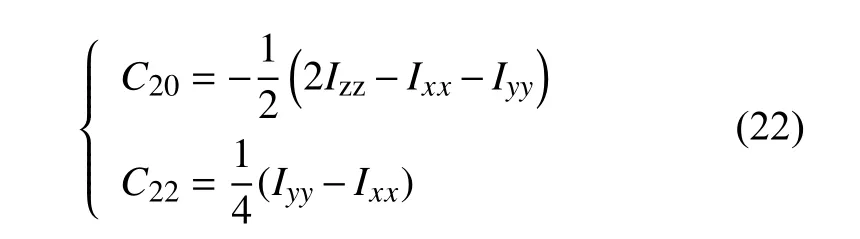
假设中心天体为椭球体，其3个主轴分别为α、β和γ，那么各个坐标轴的转动惯量为

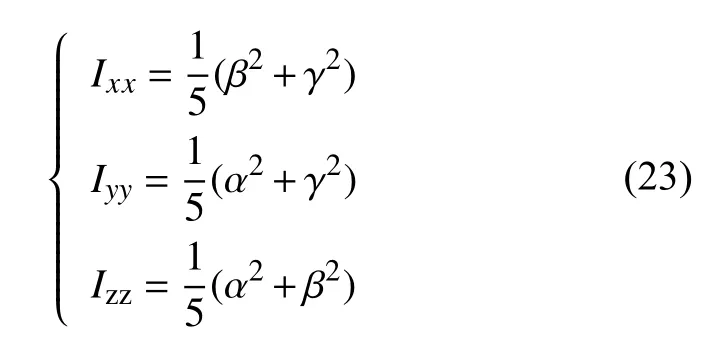
2.1 球体–球体模型

在球体–球体模型中，天体M1和M2的引力势均用球体模型来计算。则天体M1和M2的势函数为

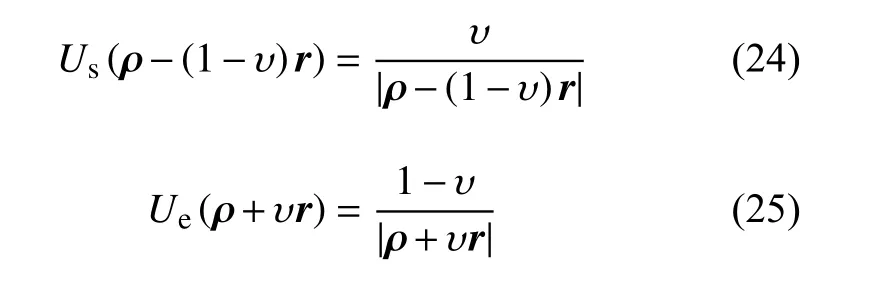
2.2 椭球体–球体模型

Bellerose在椭球体–球体模型中采用椭圆积分来计算椭球体的引力势。在本节中，改进采用计算效率高，无积分环节的二阶二次球谐函数模型计算天体的引力势。则天体M1和M2的势函数为

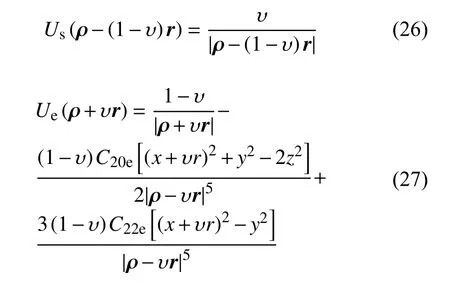
2.3 椭球体–椭球体模型

在第2.2节的椭球体–球体模型的基础上，本节提出了一种改进的限制性椭球体–椭球体模型。限制性椭球体–椭球体模型本质上是将“椭球体–球体模型”中的“球体”替换为一个“限制性椭球体”，即将球体M1改进为一个限制性椭球体，将其三轴改为并且使用二阶二次球谐函数模型来计算其引力势能，以便使更新后的双小行星系统引力场模型能更准确地描述探测器近双小行星系统动力学问题。因此，在此模型下，天体M1和M2的势函数为

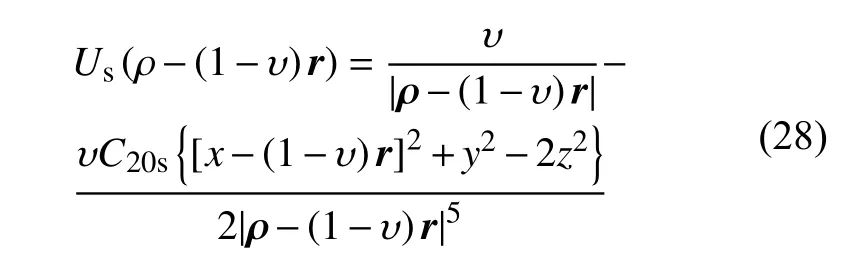
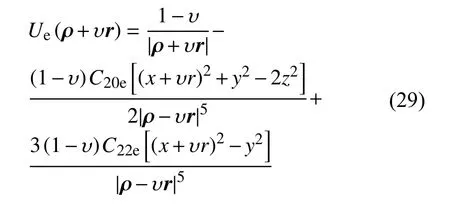
3 仿真结果

在前文中，针对弱引力双小行星系统引力场建模问题，分别采用复杂度和精度依次递增的球体–球体模型、椭球体–球体模型和限制性椭球体–椭球体模型进行建模，并分别采用椭圆积分和二阶二次球谐函数来计算其引力势能。本节针对平面圆形限制性三体问题（Circular Restricted Three-Body Problem，CRTBP），以双小行星系统1999KW4为例，分别对前文给出的不同弱引力双小行星系统引力场模型进行势能的仿真分析。双小行星系统1999KW4限制性椭球体–椭球体模型归一化后的参数如表1所示。

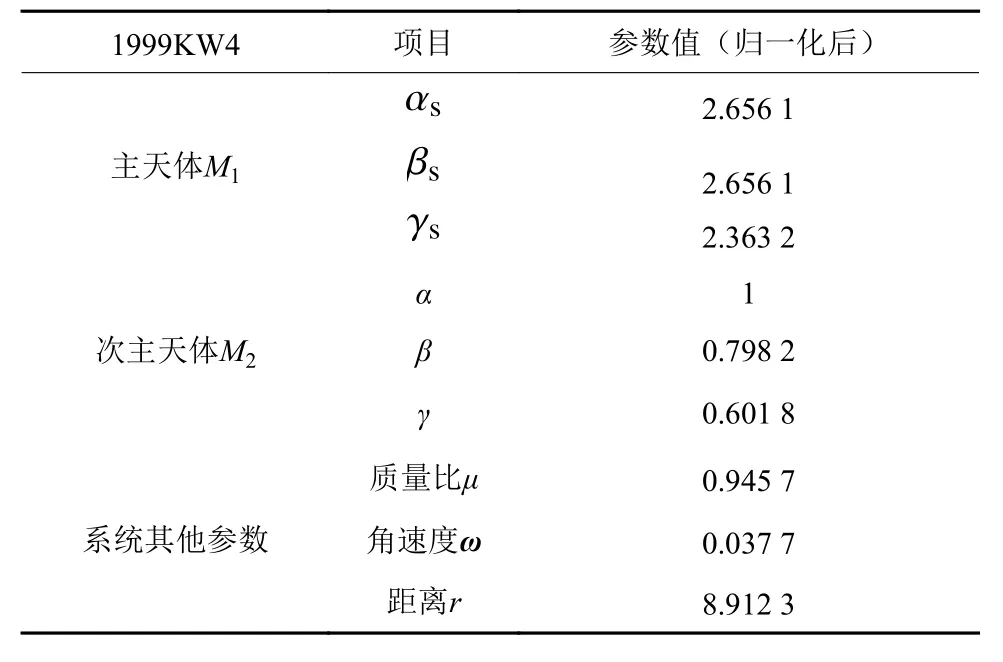
表1 双小行星系统1999KW4归一化后参数Table 1 The normalized parameters of the restricted ellipsoidellipsoid model of binary system 1999KW4

双小行星系统1999KW4中天体M1和M2的势函数分别为等效势能函数为

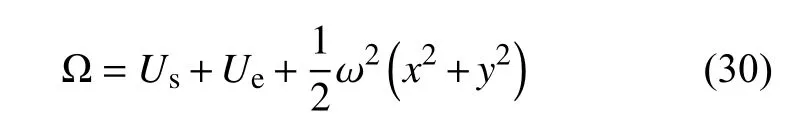
则不同引力场模型下的等效势能函数曲面分别如图5和图6所示。

由图5和图6可以看出，等效势能曲面有2个极大值点和3个鞍点（对应5个平动点），图中也画出了在不同高度（对应不同的雅克比能量）的等高线，这些等高线就是对应雅克比能量下的零速度曲线，图7以等高线图的形式更清楚地描述了零速度曲线随雅克比能量变化的情况。由图7可以看出，零速度曲线关于x轴对称，随着雅克比能量的增大，对应的可运动区域增大，并且该区域的拓扑结构也发生了变化。

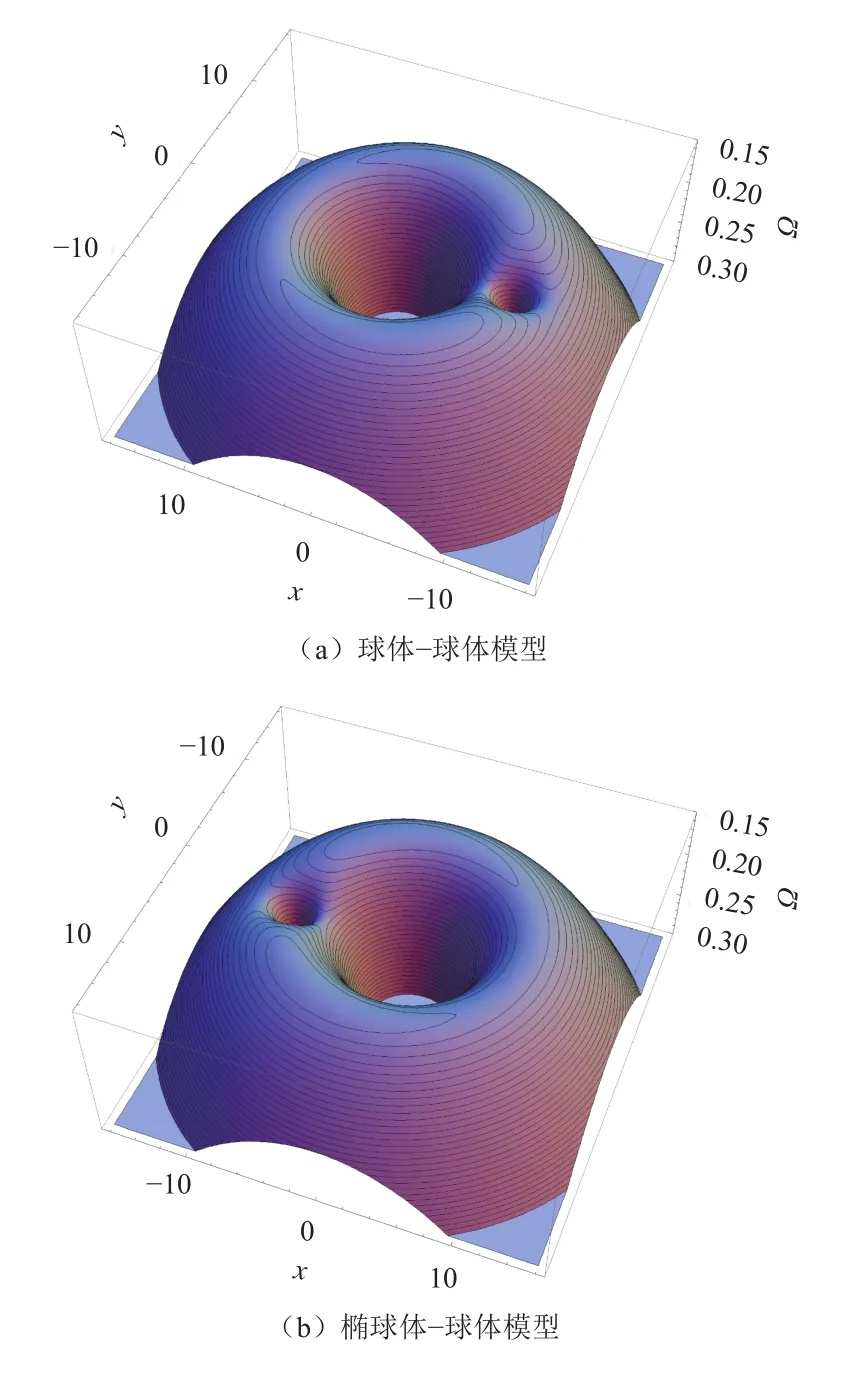
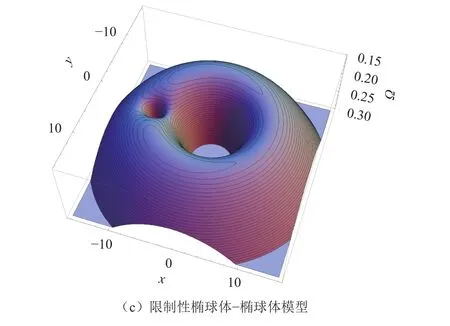
图6 平面圆形限制性三体问题等效势能函数曲面（二阶二次球谐函数计算引力势能）Fig. 6 The effective potential of CRTBP （ellipsoid potential energy is written in terms of the second degree second order spherical harmonic function）

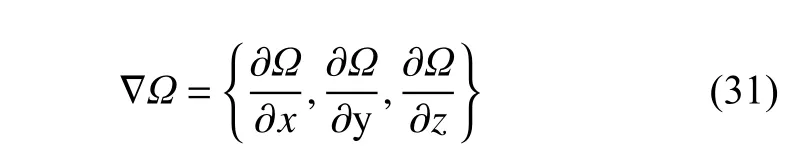
在CRTBP中，存在着5个平动点（拉格朗日点），并且拉格朗日点是梯度矢量场的零点，见式（31），该矢量场也是等效势能所产生的加速度场，不同引力势模型下的等效势能的梯度矢量场及5个拉格朗日点如图8所示。

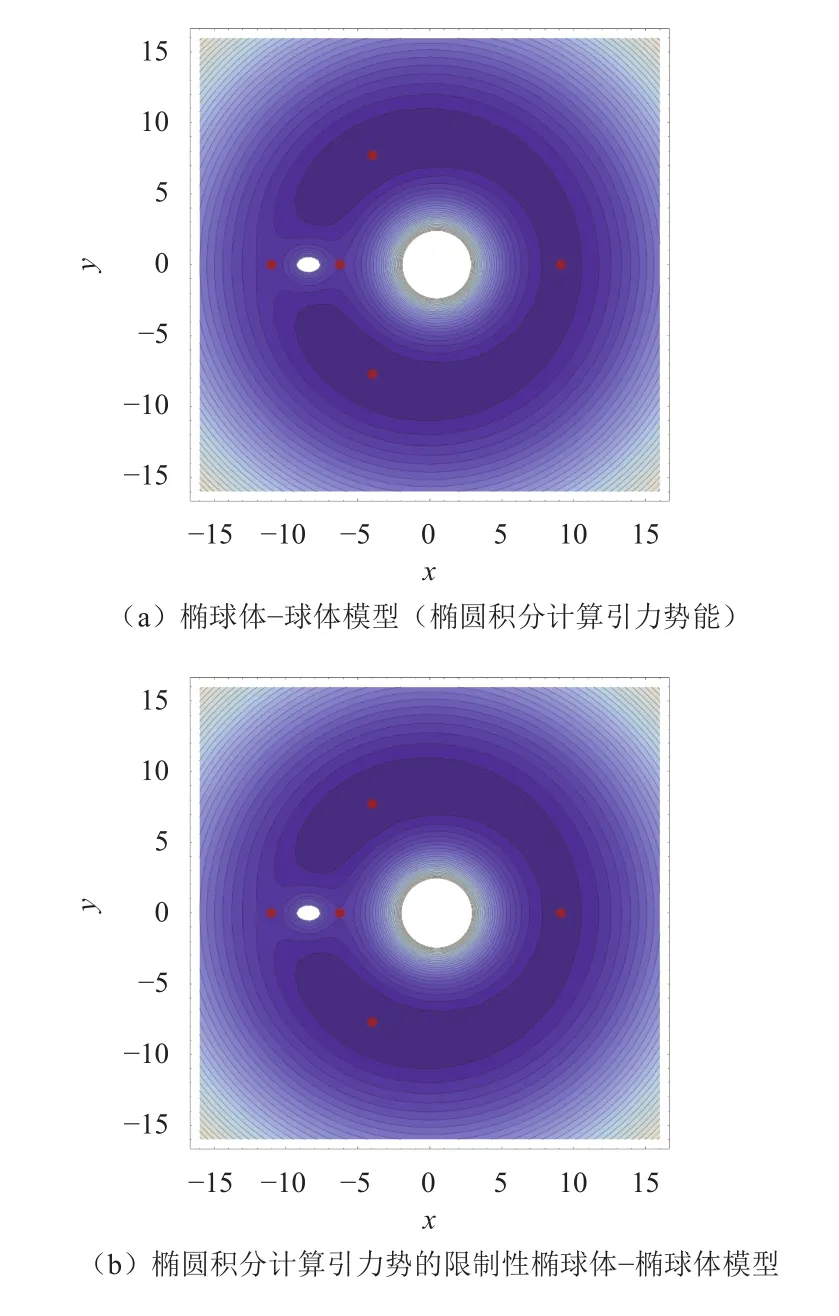
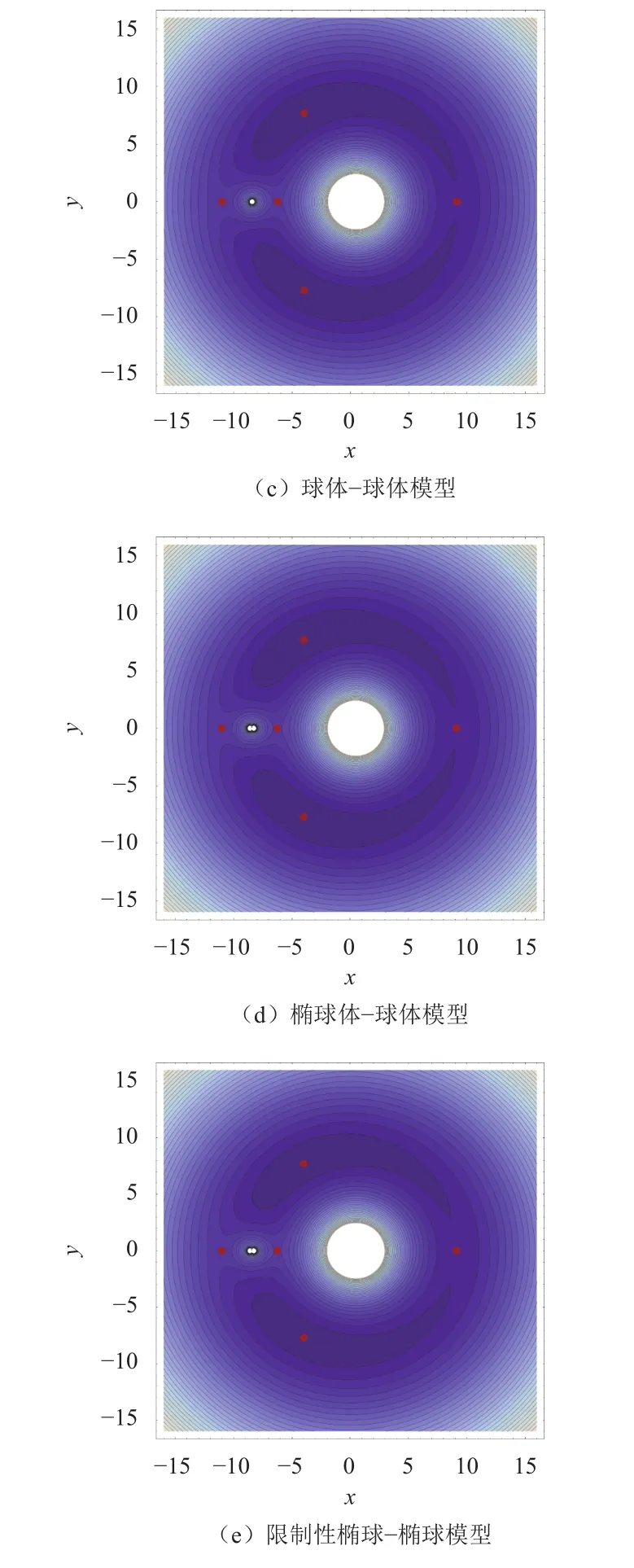
图7 平面圆形限制性三体问题等效势能函数的等高线图Fig. 7 The contours of effective potential in CRTBP

接下来以1999KW4为例分别比较不同模型下的平动点位置偏差。首先，计算由椭圆积分计算引力势的双椭球体模型下的平动点位置坐标，并与文献[9]中椭球体-球体模型的结果进行对比，结果如表2所示。然后，计算不同模型下分别由椭圆积分和由二阶二次球谐函数计算引力势的平动点位置坐标，如表3、表4所示。

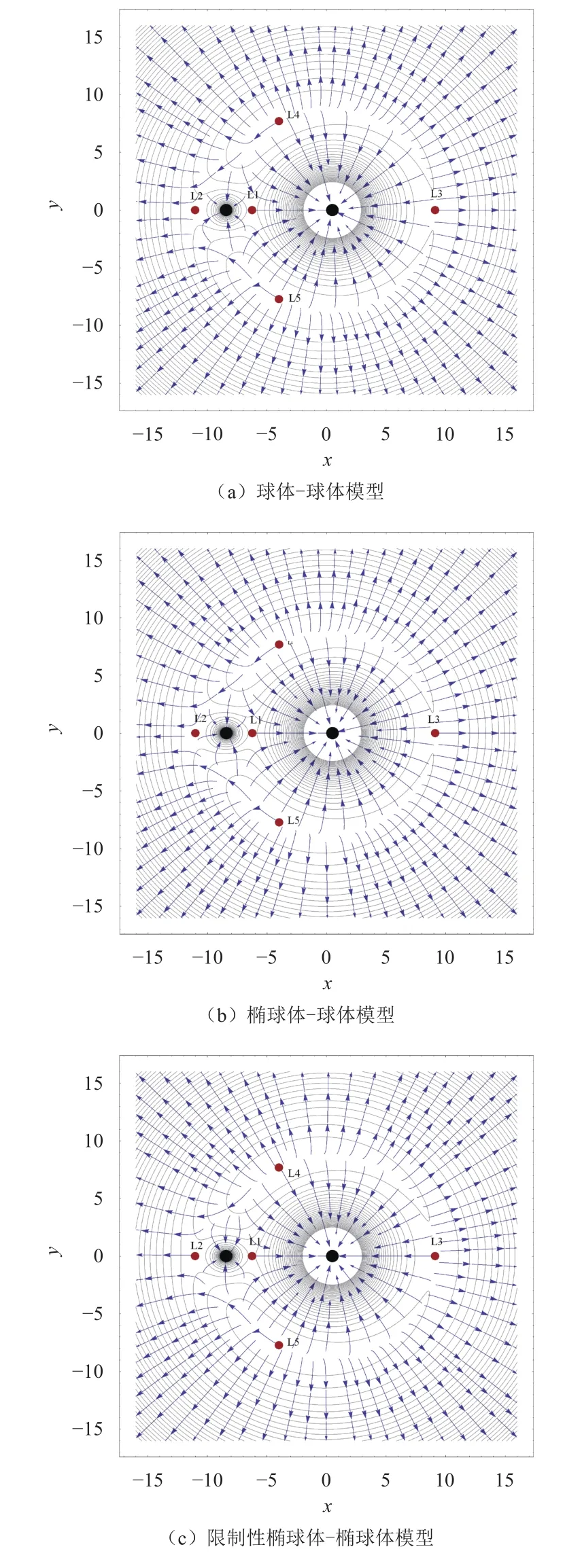
图8 等效势能的梯度矢量场及5个拉格朗日点（二阶二次球谐函数计算引力势能Fig. 8 The gradient vector field of and five Lagrangian points

观察表2可知，双椭球模型与文献[9]中椭球-球模型的平动点位置最大偏差为0.178 6 %，考虑到双椭球模型更接近于1999KW4的实际形状，因此用双椭球体模型是较为精确的。观察表3和表4，可以发现，在利用椭球体-球体模型和椭球体-椭球体模型进行双小行星系统的引力场建模时，采用椭圆积分进行计算的结果和采用二阶二次球谐函数模型进行计算的结果是十分相近的，最大偏差为0.049 7 %，因此采用二阶二次球谐函数模型进行引力势的计算也是能得到很精确的结果的。而比较计算时间，从表3中，可以看出，在椭球体-球体模型中，采用椭圆积分进行计算需要消耗0.53 s的时间，而采用二阶二次球谐函数模型进行计算消耗时间仅仅是0.015 s，远远小于0.53 s。而在椭球体-椭球体模型中，采用椭圆积分进行计算需要计算更多的积分环节，从表4可以看出，其所消耗的时间也从0.53 s增加到了1.389 s，而采用二阶二次球谐函数模型进行计算所消耗的时间并没有明显的增加，只有0.016 s，远远小于1.389 s。因此，综上所述，可以证明本文提出的二阶二次球谐函数计算引力势的椭球体-椭球体模型计算精度高，复杂程度更低，计算量更少，计算速度更快，是十分有效的。

表2 椭圆积分计算引力势的平动点位置坐标对比Table 2 Comparison of coordinates of libration points calculated by elliptic integrals

表3 椭球体-球体模型平动点位置坐标对比Table 3 Comparison of coordinates of libration points in ellipsoid - sphere model

表4 椭球体-椭球体模型平动点位置坐标对比Table 4 Comparison of coordinates of libration points in ellipsoid - ellipsoid model

4 结 论

由于双小行星系统附近的探测器动力学建模问题比较复杂，而且如果把两个小行星的不规则引力场和自旋转等因素都考虑进去就是非常复杂的全三体问题，其目前为止基本上处于无解状态。因此，针对弱引力双小行星系统的引力场建模问题，本文采用复杂度和精度依次递增的球体–球体模型、椭球体–球体模型和改进的限制性椭球体–椭球体模型来进行引力场建模，从而比较精确地刻画双小行星系统和探测器构成的限制性全三体问题的动力学模型。并针对不同的引力场建模方法进行了仿真，以双小行星系统1999KW4为例，给出了不同引力场模型下的等效势能曲面及等高线图，最后还给出了等效势能的梯度矢量场及5个拉格朗日点。最后针对不同模型下的平动点位置坐标偏差进行了比较。本文提出的二阶二次球谐函数计算引力势的椭球体–椭球体模型计算精度高，复杂程度更低，计算量更少，计算速度更快，能够较精确的对双小行星系统进行引力场建模。未来更进一步，还可以结合多面体模型法和球谐函数模型法来更精确地描述双小行星系统中不规则天体的引力场模型。

[1]Pravec P，Harris A W. Binary asteroid population：1. angular momentum content [J]. Icarus，2007，190（1）：250-259.

[2]Scheeres D J，Ostro S J，Hudson R S，et al. Orbits close to asteroid 4769 Castalia [J]. Icarus，1996，121：67-87.

[3]Scheeres D J，Ostro S J，Hudson R S，et al. Dynamics of orbits close to asteroid 4179 Toutatis [J]. Icarus，1998，132：53-79.

[4]Bellerose J，Scheeres D J. Stability of equilibrium points in the restricted full three body problem[J]. Acta Astronautica，2007，60：141-152.

[5]Fahnestock E G，Scheeres D J. Simulation of the full two rigid body problem using polyhedral mutual potential and potential derivatives approach [J]. Celestial Mechanics and Dynamical Astronomy，2006，96：317-339.

[6]Fahnestock E G，Lee T，Leok M，et al. Polyhedral potential and variational integrator computation of the full two body problem[C]//The 2006 AIAA/AAS Astrodynamics Specialist Meeting.[S.l.]：AIAA，2006.

[7]李翔宇，乔栋，崔平远. 双体小行星1996FG3捕获与逃逸轨道设计[C]//上海航天技术研究院第二届小行星探测学术研讨论文集.上海：上海航天技术研究院，2014.Li X Y，Qiao D，Cui P Y. The capture and escape trajectory design of the binary asteroid 1996FG3 [C]// The 2nd Shanghai Academy of Spaceflight Technology Asteroid Exploration Conference. Shanghai：Shanghai Academy of spaceflight Technology，2014.

[8]Bellerose J，Scheeres D J. Restricted full three-body problem：application to binary system 1999 KW4 [J]. Journal of Guidance，Control，and Dynamics，2008，31（1）：162-171.

[9]Bellerose J. The restricted full three body problem：applications to binary asteroid exploration[D]. Ann Arbor：University OF Michigan，2008.

[10]Kaula W M. Theory of satellite geodesy：applications of satellites to geodesy [M]. Mineola：Dover publications，2000：4-8.

[11]Hu W. Orbital motion in uniformly rotating second degree and order gravity fields [D]. Ann Arbor：the University of Michigan，2002.

[12]Hu W，Scheeres D J. Numerical determination of stability regions for orbital motion in uniformly rotating second degree and order gravity fields [J]. Planetary and Space Science，2004，52（8）：685-692.