环月轨道交会的载人登月任务轨道与窗口规划

贺波勇，曹鹏飞，罗亚中，李海阳

（国防科技大学 空天科学学院，长沙 410073）

0 引 言

月球是地球唯一的天然卫星，是人类进入深空最理想的中转站，因此，人类从未放弃对月球的探测[1]。1969年7月16日，美国成功发射了“阿波罗11号”（Apollo11）号载人月球飞船，实现了人类历史上的首次载人登月。2004年，美国启动了重返月球的“星座计划”，提出了“全月面到达”和“任意时刻安全返回”等新时期载人登月目标，并给出了基于环月轨道（Low Lunar Orbit，LLO）共面交会的“人货分离”载人月球探测任务方案[2-3]。美国2009年6月18日发射的月球侦察轨道器/月坑观测与探测卫星（Lunar Reconnaissance Orbiter，LRO/Lunar Crater Observation and Sensing Satellite，LCROSS）及其随行的“半人马座”上面级，成功对月球南极进行了两次撞击，发现了水冰存在的证据[4-6]，引发了载人月球极区和高纬度区域的探测热潮。

作为载人登月关键技术之一的窗口与轨道设计技术，一直是该领域的研究热点。郗晓宁[7]等较早提出了基于月球影响球参数的双二体模型下载人登月任务轨道与窗口设计方法，但精度较低，适合特性分析。李桢等[8]较早研究了基于LLO交会的奔月方案。文献[9]针对载人登月绕月自由返回任务，提出了一种轨道与窗口一体化设计方法，在双二体模型下，通过4段二体轨道拼接完成自由返回轨道初值搜索及匹配近地停泊轨道（Low Earth Orbit，LEO）月窗口，其结果作为高精度模型下序列二次规划（Sequence Quadratic Program，SQP）修正迭代初值，精度高但计算效率较低。

文献[9]提出的轨道与窗口一体化设计方法具有很好的借鉴意义，本文在此基础上，进一步研究了基于LLO共面交会的“人货分离”载人登月任务窗口与轨道一体化规划方法，分析了任务基本流程和工程约束，并针对任务各阶段窗口与轨道求解问题，提出了以动力下降时刻为迭代初值的窗口规划策略，并建立了高精度模型下的环月轨道、双二体模型下的人员和货物运输轨道规划模型。最后，通过仿真测试，文章所述方法的正确性得到了验证，为探月工程任务提供了一种有效的窗口与轨道设计工具。

1 问题描述

1.1 载人月球探测任务基本流程

考虑重型运载火箭能力，参考美国“星座计划”中“人货分离”奔月思想，采用环月轨道共面交会方式进行载人月球探测[9]，设计基本流程如图1所示。

图1 基于LLO共面交会的载人月球探测任务基本流程图Fig. 1 Basic flow chart of manned lunar mission based on LLO coplanar rendezvous

着陆器早于载人飞船从地面发射，近地轨道（LEO）短暂停留后进行地月转移近月点一脉冲捕获后进入环月圆轨道（LLO），等待载人飞船。待着陆器月球捕获完成后，载人飞船从地面发射，LEO短暂停留后采用自由返回轨道进行地月转移，一般而言，自由返回轨道近月段贴近白道面，需要预留一定时间，采用3脉冲月心大椭圆远月点附近调整轨道面，之后与着陆器LLO第一次交会对接，交会完成后形成组合体，航天员和科学考察仪器从载人飞船向着陆器转移，可以忽略动力下降和动力上升用时，初步设计时认为月面科学考察时长为为动力上升后LLO第二次交会对接，之后形成组合体，航天员和月壤等转移至载人飞船中预留0～25 h匹配着陆场经度），与月球的第3脉冲捕获类似，采用第3脉冲月球逃逸第3脉冲进入月地返回轨道）为从再入点到着陆地面的时间。

1.2 工程约束

载人月球探测除受到自然环境约束外，工程可实现性也会带来一些约束。工程约束并非一成不变，在航天技术快速发展的步伐下，现在的约束必然会在未来失去约束性。郑爱武、周建平等[10]概述了载人登月轨道基本工程约束条件。

在文献[10]基础上，共面动力下降和动力上升会限定环月圆轨道；定点返回地球某指定着陆场也会带来约束，如定点返回四子王旗着陆场，便于对航天员进行紧急搜救，会要求月地返回时刻月球赤纬在南纬较低值；为给月面科考留充足月昼时长，月面动力下降时刻选在月昼早晨，如果测高和地形匹配系统对阳光入射角有严格约束（如图2所示，“Apollo11”任务要求5～14°），则动力下降窗口被约束在较小范围[12]。着陆器和自由返回轨道从某发射场发射，地月转移轨道倾角根据发射场纬度和射向角计算，为确定值。总之，工程约束要根据飞行器实际性能决定。

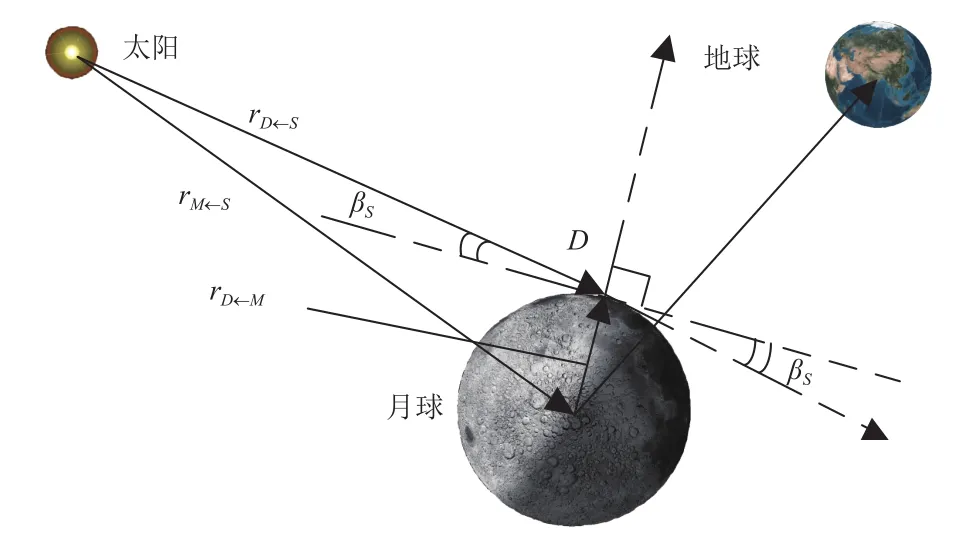
图2 阳光入射角示意图Fig. 2 Sketch of solar angle

2 任务窗口与轨道规划

2.1 任务窗口规划

综合分析基于LLO共面交会的载人登月任务基本流程、客观存在的地月空间环境约束和未来一段时间仍可预见的工程约束等，分析归纳任务窗口轨道问题包含3个近似等式约束：①月面动力下降阳光入射角约束；②自由返回轨道地月转移入轨时刻（Trans-Lunar Injection，TLI），地心J2000坐标系中轨道倾角约束；③月地定点返回轨道月地转移入轨时刻（Trans-Earth Injection，TEI），月球赤纬和返回着陆场纬度相关约束。

考虑上述3个苛刻的工程约束，设计任务窗口规划基本策略如图3所示。第1步：设定和，初始化计算该时刻月面着陆点阳光入射角如果不满足约束，以步长调整直到满足阳光入射角约束为止；第2步：进入第2个约束判断阶段，由计算通过下文2.2.2小节自由返回轨道设计方法求解TLI时刻地心J2000坐标系中轨道倾角如果不满足约束，以步长调整直到约束满足为止；第3步：进入第3个约束判断阶段，由计算由于预留0～25 h匹配着陆场经度有两个极大极小值进行两次月地定点返回轨道设计，当两次计算的再入点地心J2000坐标系中倾角都大于着陆场纬度时，终止计算，存储所有计算数据，否则，以步长直到约束满足为止。

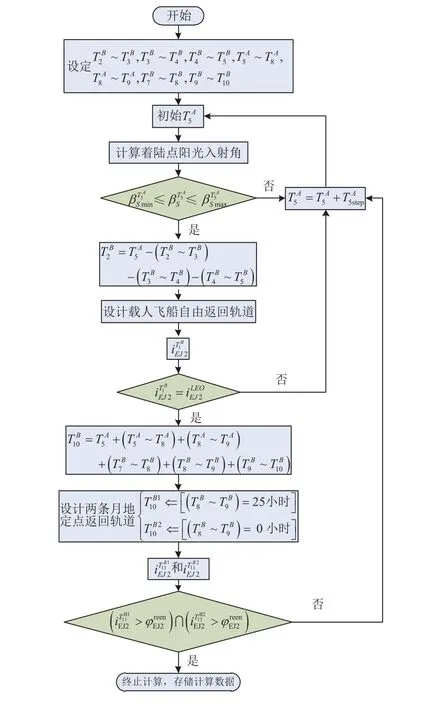
图3 任务窗口规划基本策略Fig. 3 Basic strategy for planning windows

该任务规划策略未包含着陆器地月转移窗口及轨道参数计算流程，原因是着陆器没有航天生保系统约束，设计范围无约束，一般而言，一个月内存在降轨和升轨两次月窗口，如果着陆器和载人飞船采用同一个发射场，工程指挥部门倾向于选用前一次月窗口，给载人飞船发射预留充足的地面准备时间。

2.2 任务轨道规划

本节立足载人登月“人货分离”任务总体，给出各阶段轨道规划方法，公式推导可参考文献[9～11]，这里不再赘述。

2.2.1 环月轨道规划

基于球面三角和二体轨道解析公式的高精度LLO求解结果会因月球天平动而存在误差，这里采用高精度动力学模型求解：首先，计算动力下降时刻着陆点在月心J2000坐标系中位置其次，计算动力上升时刻着陆点在月心J2000坐标系中位置LLO高则按照轨道六根数定义，有

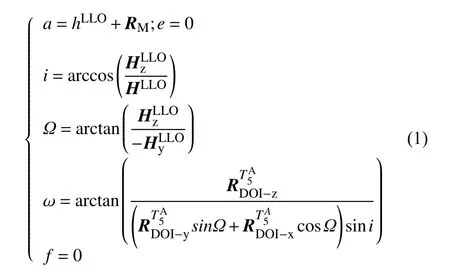
2.2.2 载人登月任务轨道规划

自由返回轨道地月转移和月地返回段用时均约3天，双二体假设模型与高精度模型误差较小，以近月点参数为设计变量，分别以TLI时刻地心距和再入地球时刻真空近地距、TLI时刻地心J2000坐标系中倾角为加权目标函数，构建优化问题，如下所示

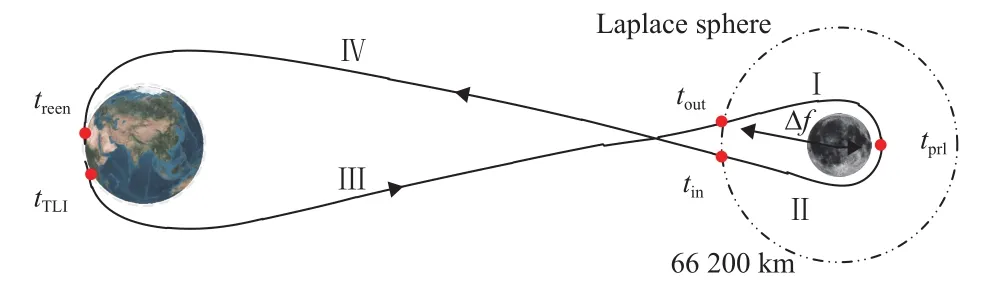
图4 四段二体轨道拼接法Fig. 4 Patched conic technique based on the double two-body model

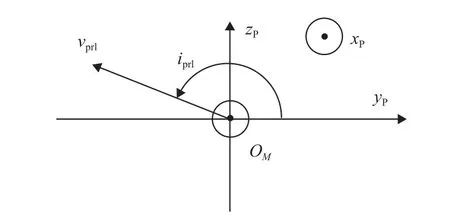
图5 近月点坐标系速度示意图Fig. 5 Sketch of velocity vector in perilune coordinate system

2.2.3 定点返回轨道求解模型

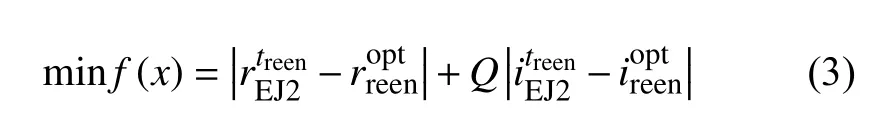
2.2.4 着陆器货运任务轨道规划

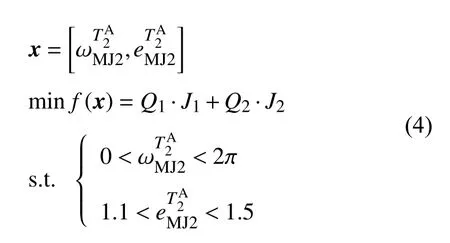
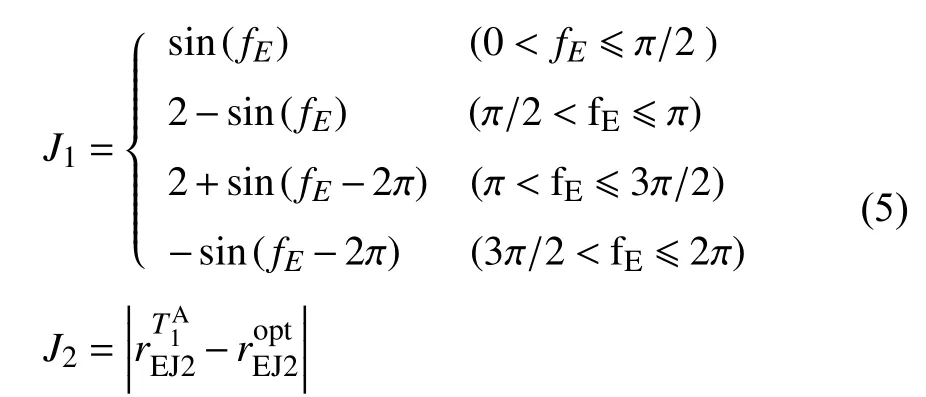
3 算例分析与验证

月球背面及高纬度探测，是当前月球开发研究热点，本节以载人月球背面探测环形山（以中国科学家命名）为例，给出轨道与窗口仿真实例。月面上共有6处环形山是以中国科学家命名的，均位于月球背面，位置信息如表1 所示，既有低纬度区域，也有中高纬度区域。

表1 月球背面中国科学家命名环形山经纬度Table 1 The latitude and longitude of the ring mountain named by Chinese scientists on the back of the moon

以石申环形山区域（105°E，76°N）为例，假定任务年份为2030年，参数设置如下：=3天）、=0.5天）和初始化为1 Jan 2030 0:00:00.000 UTCG步长（参考文昌发射场），（参考四子王旗着陆场）。仿真在Intel Core 2 T6400 2.00 GHz 2.00 GB内存PC机上VC++6.0环境下进行。

采用SQP_Snopt算法[12]求解窗口及任务转移轨道参数，共用时2 330 s，结果如表2所示，其中，ModOrb-Elem表示修正轨道六根数。由表2可知，2030年共存在4次月窗口机会，分析原因：着陆点阳光入射角限制在5～14°、近地倾角匹配20°和返回轨道倾角大于45°，3个苛刻约束条件导致月窗口交集变小。

4 结论与展望

针对环月轨道共面交会支持的“人货分离”载人登月任务，提出了一种任务窗口与轨道一体化快速规划方法。分析了任务基本流程和工程约束，并针对任务各阶段窗口与轨道求解问题，提出了以动力下降时刻为迭代初值的窗口规划策略。建立了高精度模型下的环月轨道、双二体模型下的人员和货物运输轨道规划模型。最后，以月球背面高纬度探测为假想背景，给出仿真实例，仿真数据表明了文章所述方法的有效性和快速性。进一步研究发现，基于LLO交会的载人登月任务流程复杂，各个阶段约束条件多，任务年份内月窗口并非每个月都有，需要根据约束条件，具体建模求解。

表2 双二体模型求解窗口及轨道参数Table 2 Window and trajectory parameters computed by the double two-body model

[1]龙乐豪，容易. 现代“嫦娥奔月”的技术途径设想[J]. 导弹与航天运载技术，2008，293（1）：1-7.Long L H，Rong Y. Research on the technical approach of manned lunar mission [J]. Missiles and Space Vehicles，2008，293（1）：1-7.

[2]Mindell D A. The futrue of human spaceflight [R]. Space，Policy，and Society Research Group. Cam-bridge：MIT，2008.

[3]Garn M，Qu M，Chrone J，et al. NASA’s planned return to the moon：global access and anytime return requirement implications on the lunar orbit insertion burns [C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.[S.l.]：AIAA，2008.

[4]Colaprete A，Schultz P，Heldmann J，et al. Detection of water in the LCROSS ejecta plume[J]. Science，2010，330（6003）：463-468.

[5]Mitrofanov I G，Sanin A B，Boynton W V，et al. Hydrogen mapping of the lunar south pole using the LRO neutron detector experiment LEND[J]. Science，2010，330（6003）：483-486.

[6]Sridharan R，Ahmed S M，Das T P，et al. Direct evidence for water in the sunlit lunar ambience from CHACE on MIP of chandrayaan I[J].Planetary and Space Science，2010，58（6）：947-950.

[7]郗晓宁，曾国强，任萱，等. 月球探测器轨道设计[M]. 北京:国防工业出版社，2001.Xi X N，Zeng G Q，Ren X，et al. Orbit design of lunar probe [M].Beijing:National Defense Industry Press，2001.

[8]李桢，周建平，程文科，等. 环月轨道交会的奔月方案[J]. 国防科技大学学报，2009，31（1）：16-20.Li Z，Zhou J P，Cheng W K，et al. Investigation on lunar mission based on lunar orbit rendezvous [J]. Journal of National University of Defense Technology，2009，31（1）：16-20.

[9]贺波勇，李海阳，周建平. 载人登月绕月自由返回轨道与窗口精确快速设计[J]. 宇航学报，2016，37（5）：512-518.He B Y，Li H Y，Zhou J P. Rapid design of circumlunar free-return high accuracy trajectories and trans-lunar window for manned lunar landing mission[J]. Journal of Astronautics，2016，37（5）：512-518.

[10]郑爱武，周建平. 载人登月轨道设计方法及其约束条件概述[J]. 载人航天. 2012，18（1）：48-54.Zheng A W，Zhou J P. A survey on trajectory design and constrains of manned lunar landing missions[J]. Manned Spaceflight，2012，18（1）：48-54.

[11]贺波勇，李海阳，沈红新，等. 载人登月着陆窗口与定点返回轨道耦合设计[J]. 国防科技大学学报，2017，39（1）：11-16.He B Y，Li H Y，Shen H X，et al. Coupled design of landing window and point return orbit for manned lunar landing mission [J]. Journal of National University of Defense Technology，2017，39（1）：11-16.

[12]Philip E G，Murray W，Saunders M A. SNOPT：an SQP algorithm for large-scale constrained optimization [J]. SIAM J Optim，2002，12（4）：979-1006.