考虑瞬态冲击和弹性变形的滑动轴承特性与动力学响应

张胜伦, 裴世源, 徐华,2, 张亚宾, 朱杰

(1.西安交通大学现代设计及转子轴承系统教育部重点实验室, 710049, 西安;2.新疆大学机械工程学院, 830046, 乌鲁木齐; 3.湖南崇德工业科技有限公司, 411228, 湖南湘潭)

考虑瞬态冲击和弹性变形的滑动轴承特性与动力学响应

张胜伦1, 裴世源1, 徐华1,2, 张亚宾3, 朱杰3

(1.西安交通大学现代设计及转子轴承系统教育部重点实验室, 710049, 西安;2.新疆大学机械工程学院, 830046, 乌鲁木齐; 3.湖南崇德工业科技有限公司, 411228, 湖南湘潭)

同时考虑瞬态冲击载荷和轴瓦的弹性变形,模拟了舰船在风浪拍击时推进轴支承滑动轴承的润滑特性与动力学响应,研究了聚四氟乙烯(PTFE)弹性金属塑料瓦滑动轴承的最小油膜厚度、最大油膜压力和轴心轨迹随时间的变化情况。运用有限元法求解雷诺方程,将油膜力转化为轴瓦节点力计算了弹性变形;用欧拉法求解轴颈的动力学方程,计算了动态轴心轨迹。对比了刚性瓦与PTFE弹塑瓦滑动轴承的特性,结果表明,轴瓦弹性变形对油膜厚度和油膜压力分布的影响不可忽略,并且轴瓦弹性变形可以提高滑动轴承的承载能力。对比分析了4个不同方向瞬态冲击载荷作用下PTFE弹塑瓦滑动轴承的特性和轴颈的动态轴心轨迹,提出可通过改变轴承静载荷方向、减小瞬态冲击载荷方向与轴承偏心方向的夹角来增加最小油膜厚度,降低最大油膜压力,减小动态轴心轨迹的位移响应振幅,进而改善滑动轴承润滑状态,减小轴瓦的弹性变形量,提高轴承-转子系统的稳定性。

滑动轴承;瞬态冲击载荷;弹性变形;动力学响应

舰船作为一种重要的水上交通工具,在民用、运输以及军事等领域具有极其重要的地位。由于舰船处于海上风浪拍击的特殊环境中,船体会受到冲击力的剧烈作用,这种冲击力最终将转化为安装于船体的推进轴支承滑动轴承与推进轴轴颈的相互作用力和相对位移。推进轴在受到如此剧烈的瞬态冲击载荷时,极易与轴瓦直接接触,从而导致烧瓦、抱轴等重大事故。

国内外学者已经对瞬态冲击载荷下的滑动轴承特性进行了不少研究,例如:马金奎等研究了不同脉冲波形作用下轴承最小油膜厚度、最大油膜压力、轴心轨迹等的变化情况[1];Rao等计算了冲击激励在稳态、临界转速、失稳转速3种情况下产生的轴心轨迹,并分析了冲击激励对轴承-转子系统动力学性能的影响[2];Tichy和Bou-Saïd研究了横向瞬态冲击载荷的大小和作用时间对轴心动态轨迹的影响[3];李震等研究了轴承-转子系统在瞬态冲击载荷、正弦载荷、旋转载荷等激励条件下的共振现象[4]。以上工作在一定程度上揭示了不同冲击载荷类型和参数作用下的滑动轴承轴心轨迹和轴承-转子系统稳定性,相关研究方法和成果对本文均具有指导意义。

弹性金属塑料轴瓦(EMP),简称弹塑瓦,广泛应用于舰船推进轴支承滑动轴承。弹塑瓦是由聚四氟乙烯(PTFE)与弹性青铜丝复合镶嵌、钎焊在钢质瓦基上的新型复合轴瓦。在持续时间短暂、释放能量巨大的瞬态冲击载荷下,油膜的压力在瞬间增大至数十MPa,弹塑瓦的弹性变形将成为影响润滑特性和转子动力学响应不可忽略的重要因素。文献[5]在研究径向轴承的不平衡扰动瞬态过程中考虑了弹性变形,认为弹性变形对轴心轨迹有较大的影响。文献[6-7]的研究用PTFE代替金属瓦用于推力轴承,由于PTFE较大的弹性变形显著提高了轴承的承载能力,其表面滑移作用使得油膜温度显著降低,自润滑特性还降低了摩擦功耗。文献[8-9]分别将PTFE弹塑瓦用于静载荷作用下径向滑动轴承和可倾瓦轴承的润滑特性计算。文献[10]用有限元法求解了弹塑瓦径向滑动轴承的弹性变形和热变形。以上工作建立了弹塑瓦轴承的基本研究方法和理论。

上述研究分别在滑动轴承瞬态冲击响应和轴瓦弹性变形方面取得了有意义的成果,但综合考虑这2种因素对舰船推进轴支承滑动轴承进行润滑特性和动力学研究却鲜见报道。

本文在同时考虑瞬态冲击载荷和弹塑瓦弹性变形的条件下,深入研究了舰船推进轴支承滑动轴承的润滑特性和动力学响应,对比分析了刚性瓦和PTFE弹塑瓦在轴颈外载荷为静载荷和瞬态冲击载荷2种条件下的油膜厚度和油膜压力分布,进而研究了考虑轴瓦弹性变形条件下瞬态冲击载荷的方向对轴颈位移响应的影响。

1 建立计算模型

将雷诺方程与轴颈动力学方程联立求解,建立用于模拟舰船推进轴在受到瞬态冲击过程中轴心动态位移响应的计算模型。图1所示为滑动轴承计算模型示意图,图中将轴承中心作为坐标的原点。

图1 滑动轴承计算模型示意图

运用有限元法求解雷诺方程,并将油膜力转化为弹塑瓦有限元计算的节点力,求得的弹性变形位移量作为油膜厚度方程的修正项,再次求解雷诺方程,如此循环迭代,以求解油膜压力和弹塑瓦的弹性变形。

图2所示为对PTFE弹塑瓦进行有限元计算时的网格划分结果,其中s为PTFE弹塑层的厚度,tb为钢质基体层的厚度。将油膜力和等效转子质量作为轴颈所受的外力,用欧拉法求解轴颈的动力学方程,可得到轴颈的动态轴心轨迹。

图2 有限元计算的网格划分结果

不可压缩流体润滑剂在层流状态下的二维雷诺方程[11]为

(1)

下游边界条件为雷诺边界

轴承两端

起始边界

φ=0,p=0

终止边界

以上各式中:φ为周向坐标;z为轴向坐标;r为轴颈半径;l为轴承宽度;ω为轴颈转速;ρ为润滑剂密度;μ为润滑剂动力黏度;h为油膜厚度;p为油膜压力。

油膜厚度方程为

h=c+ecosφ+δ

(2)

式中:c为轴承的半径间隙;e为轴颈偏心距;δ为弹性变形量[8],是将油膜压力导入有限元网格上的节点力所求得的弹性变形。在计算油膜厚度时,将弹性变形作为修正项加到油膜厚度方程的右端。

轴瓦的弹性变形用赫兹接触理论[12]求得

(3)

黏温关系采用Vogel黏温方程[13]

η=η0exp[a/(b+T0)]

(4)

式中:T0为环境温度,这里认为T0等于供油温度Ts;η0是温度为T0时的黏度;a为常数;b表示“无限黏度”温度。

由于瞬态冲击载荷引起的油膜压力最大值约为数十MPa,所以润滑油密度的变化在10-5量级,本文中不予考虑。

轴颈的动力学方程为

(5)

用欧拉逐步积分法求解以上动力学方程[1],可得到新的轴心位置

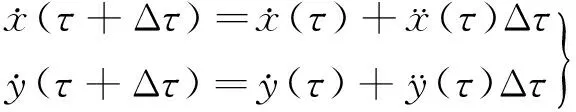
(6)

(7)

式中:Δτ为计算时间步;τ为计算总时长。

利用新的轴心位置求得新的油膜厚度,并将新的油膜厚度再次带入雷诺方程进行求解。如此循环迭代,直至达到设定的总求解时长后结束。将每个时间步所求得的轴心位置相连接,即为设定求解时间内的轴心轨迹。

图3为动态润滑计算程序的流程图。

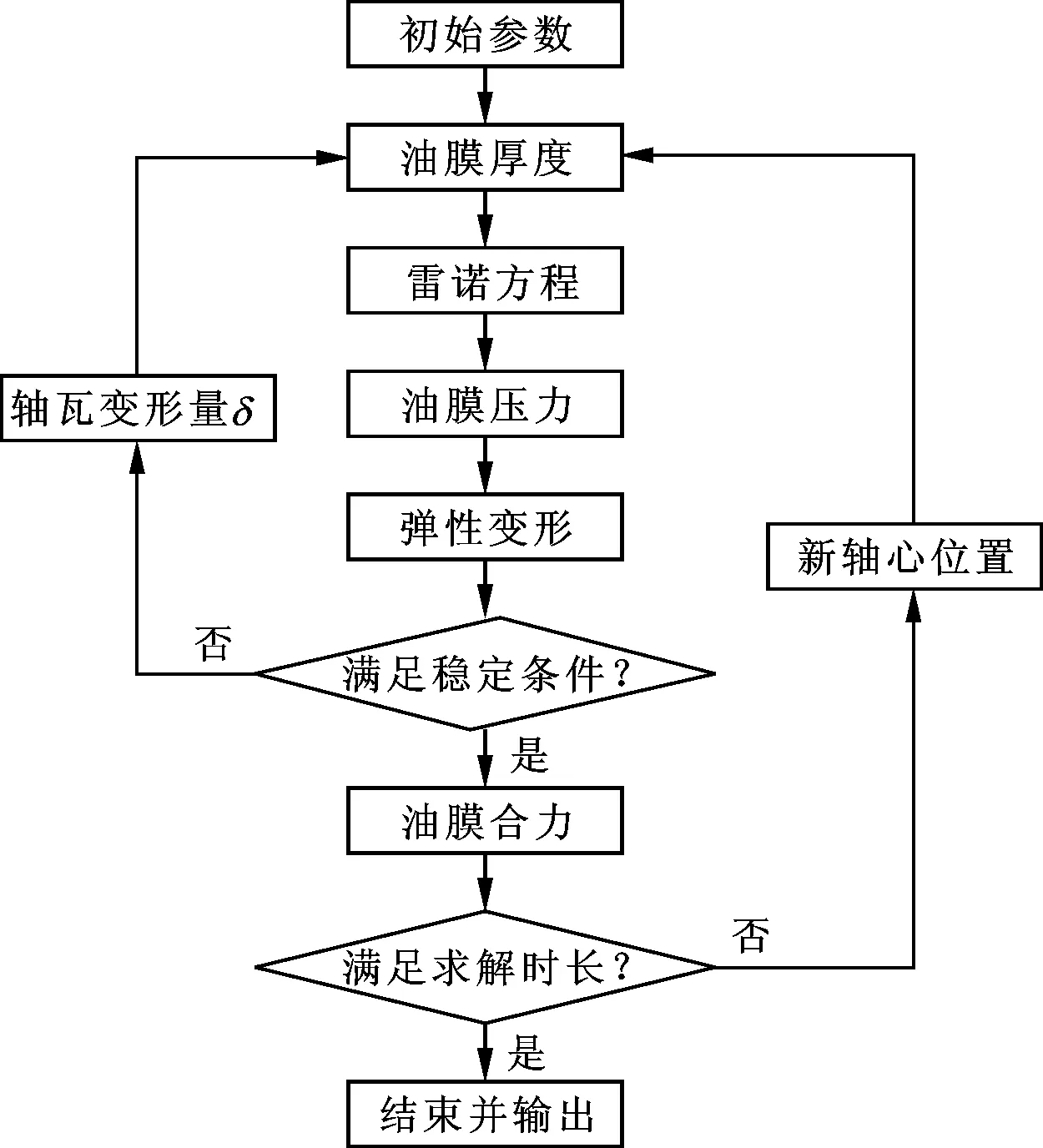
图3 动态润滑计算程序流程图

2 计算结果与分析

在舰船推进轴支承滑动轴承的润滑状态参数中,最小油膜厚度是最重要的性能指标之一,如果最小油膜厚度过小,则推进轴在运行过程中有可能与轴瓦发生擦碰。滑动轴承的承载能力主要取决于最大油膜压力,在相同载荷条件下,最大油膜压力越低,其承载能力越高。下面将分别计算刚性瓦和PTFE弹塑瓦在静载荷、瞬态冲击载荷2种工况下的最小油膜厚度和最大油膜压力,并对计算结果进行分析对比。

在建立的数值计算模型中,选取工业润滑油牌号为VG68;Vogel黏温方程(3)中的a取870.9,b取84.45;设置静载荷为等效转子质量所受的重力。刚性瓦不考虑轴瓦的弹性变形,PTFE弹塑瓦考虑轴瓦的弹性变形。轴承计算模型的参数如下:轴颈半径r=250 mm;轴承宽度l=320 mm;等效转子质量M=2 500 kg;弹塑层厚度s=7 mm;弹塑层杨氏模量E1=2 GPa;弹塑层泊松比ν1=0.4;基体层厚度tb=40 mm;基体层杨氏模量E2=211 GPa;基体层泊松比ν2=0.3;半径间隙c=270 μm;转速ω=300 r/min;进油温度Ts=42 ℃。

2.1 轴瓦弹性变形对滑动轴承特性的影响

在等效转子质量为2 500 kg、静载荷条件下,分别对刚性瓦和PTFE弹塑瓦滑动轴承的特性进行计算,结果如图4所示。

由图4a可见,刚性瓦和PTFE弹塑瓦轴向中间截面的油膜厚度周向分布基本一致,只有在周向角200°附近相差较大,刚性瓦、PTFE弹塑瓦在轴向中间截面的最小油膜厚度分别为62.5和65.8 μm。由图4c可知,周向角200°附近为油膜压力峰值分布区域,所以此处油膜厚度的变化是由于较大的油膜压力作用于PTFE弹塑瓦引起的弹性变形所导致。

由图4b可以看出,PTFE弹塑瓦的最小油膜厚度最小值为61.1 μm,最大值为65.8 μm;刚性瓦的最小油膜厚度为恒定值62.5 μm。在轴向,刚性瓦的最小油膜厚度为恒定值,而PTFE弹塑瓦的最小油膜厚度分布是与油膜压力成正比的曲线。在轴承中间截面上,PTFE弹塑瓦的最小油膜厚度比刚性瓦的大;在轴承两侧端面上,PTFE弹塑瓦的最小油膜厚度比刚性瓦的小。这是由于PTFE弹塑瓦在轴向中间截面发生凹陷、轴承两侧端面发生向上翘曲所导致的,但此时的油膜厚度足以隔离舰船推进轴与轴瓦使其不发生擦碰。

由图4c可以看出,刚性瓦的最大油膜压力为5.25 MPa,PTFE弹塑瓦的最大油膜压力为4.83 MPa。在相同静载荷的条件下,PTFE弹塑瓦的最大油膜压力比刚性瓦的低,这是由于PTFE弹塑瓦的弹性变形使得其承载面积比刚性瓦的大,因此PTFE弹塑瓦轴承的承载能力比刚性瓦轴承的承载能力强。

(a)轴向中间截面的油膜厚度周向分布 (b)最小油膜厚度的轴向分布

(c)轴向中间截面的油膜压力周向分布 (d)轴向中间截面的PTFE弹塑瓦弹性变形周向分布图4 2种滑动轴承的特性在静载荷下的计算结果对比

图4d所示为PTFE弹塑瓦在轴向中间截面的弹性变形周向分布,可知最大变形量为7.9 μm,其所在的周向角度位置与最大油膜压力位置相对应。

在等效转子质量为2 500 kg、静载荷的基础上,施加y向加载于轴颈的瞬态半正弦波冲击载荷,作用时间为0.01 s,最大峰值为250 kN,是静载荷的10倍,用来模拟风浪拍击对舰船推进轴的冲击作用。

y向瞬态冲击载荷曲线示意图如图5所示,表达式如下

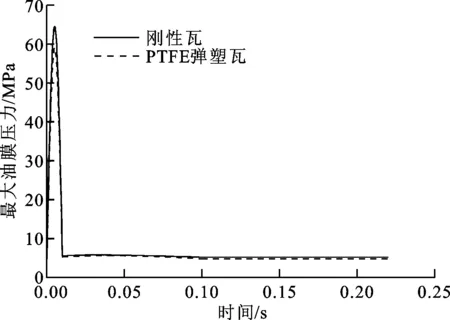
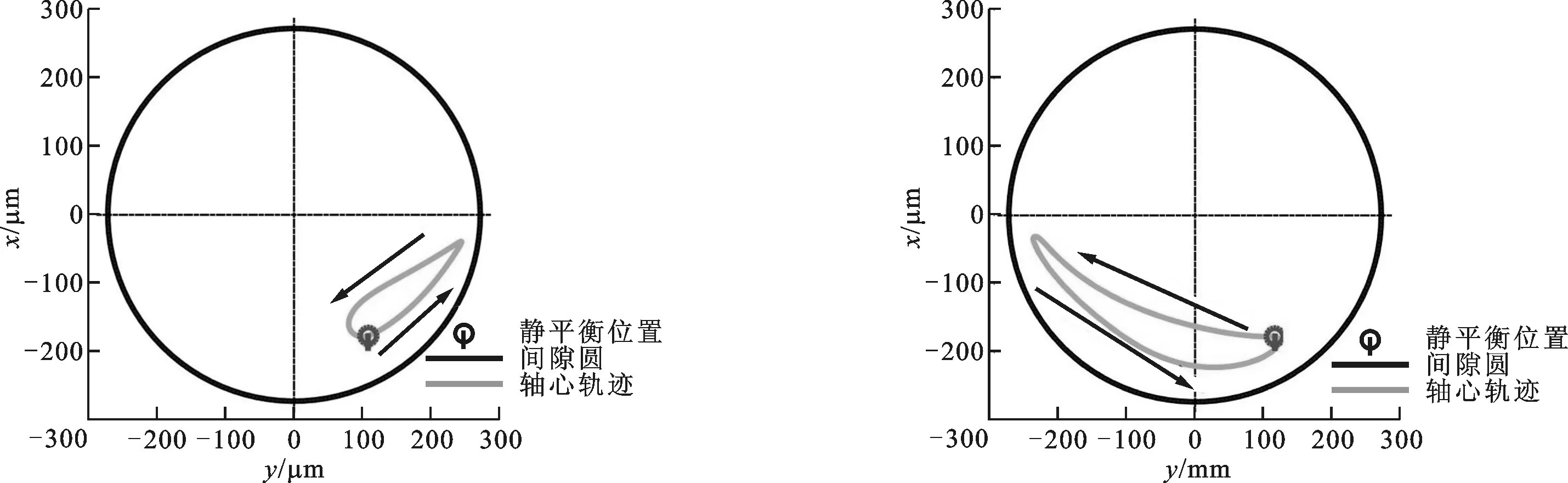
Qx=0, 0

(8)

(9)

图5 y向瞬态冲击载荷示意图

刚性瓦和PTFE弹塑瓦在施加瞬态冲击载荷后0.225 s内,最小油膜厚度随时间的变化曲线如图6a所示。从图中可以看出,由于瞬态冲击载荷作用时间短,冲击力大,最小油膜厚度在瞬时冲击发生后急剧减小,刚性瓦在0.036 s达到最小值37.1 μm,PTFE弹塑瓦在0.028 s达到最小值34.0 μm。由于惯性作用,轴颈在瞬态冲击载荷过后将继续沿载荷方向运动一段时间,因此最小油膜厚度最小值出现在冲击载荷结束之后的某一时间。由于PTFE弹塑瓦在冲击载荷之后具有较大的弹性变形,相对于刚性瓦来说承载能力更大,在冲击载荷结束之后,PTFE弹塑瓦抵抗轴颈惯性运动的能力也更大,所以最小油膜厚度随时间的变化曲线出现拐点的时间比刚性瓦更早。PTFE弹塑瓦的最小油膜厚度最小值小于刚性瓦的最小油膜厚度最小值,这是由于弹性变形引起轴承端面翘曲所致。在0.15 s之后,最小油膜厚度均趋于静载荷条件下的稳态值,刚性瓦的为62.3 μm,PTFE弹塑瓦的为60.9 μm。

(a)最小油膜厚度

(b)最大油膜压力图6 瞬态冲击载荷作用下最小油膜厚度、最大油膜压力随时间的变化曲线

刚性瓦和PTFE弹塑瓦在施加瞬态冲击载荷后0.225 s内,最大油膜压力随时间的变化曲线如图6b所示。从图中可以看出,最大油膜压力在0.005 s出现瞬时峰值,刚性瓦和PTFE弹塑瓦的最大油膜压力分别为64.74和59.22 MPa,且大小分别约为静载荷条件下最大油膜压力的12.3倍。在0.01 s后瞬态冲击载荷结束,最大油膜压力均趋于静载荷条件下的稳态值。

由于轴瓦的弹性变形与油膜压力成正比,因此PTFE弹塑瓦的最大弹性变形量随时间的分布曲线与最大油膜压力随时间的分布曲线一致。在0.005 s时PTFE弹塑瓦的最大弹性变形最大值为95.1 μm,相对于轴承半径间隙270 μm,弹性变形对油膜厚度分布和油膜压力分布的影响不可忽略。

2.2 瞬态冲击载荷方向对轴心位移响应的影响

在等效转子质量为2 500 kg、静载荷条件的基础上,施加加载于轴颈的半正弦波瞬态冲击载荷,载荷作用时间为0.01 s,最大峰值为250 kN;设置x+、x-、y+、y-四个不同的瞬态冲击载荷方向,上角标+、-分别表示沿、逆坐标轴方向。

静载荷条件下轴心的静平衡位置坐标为x=105.3 μm,y=-179.0 μm。本文规定:轴颈偏心方向为由轴承中心指向静载荷条件下的静平衡位置;瞬态冲击载荷Q(以y-方向为例)与轴径偏心方向De的夹角称为“载偏角”,用γ表示。以轴承中心为圆心、半径间隙c为半径建立间隙圆,如图7所示。因此,当瞬态冲击载荷分别为x+、x-、y+、y-方向时,载偏角γ分别为59.6°、120.4°、149.6°、30.4°。

图7 静平衡位置、间隙圆及载偏角示意图

图8所示为4个不同方向瞬态冲击载荷作用下PTFE弹塑瓦的最小油膜厚度、最大油膜压力随时间的变化曲线。

(a)最小油膜厚度

(b)最大油膜压力图8 瞬态冲击载荷下最小油膜厚度、最大油膜压力随时间的变化曲线

由图8a可见:当瞬态冲击载荷为x+方向时,最小油膜厚度在施加瞬态冲击载荷后0.01 s时达到最小值15.6 μm,在0.14 s之后趋于静载荷条件下的稳态值;当瞬态冲击载荷为x-方向时,最小油膜厚度在施加瞬态冲击载荷后0.01 s时达到最小值18.0 μm,在0.22 s之后趋于静载荷条件下的稳态值;当瞬态冲击载荷为y+方向时,在施加瞬态冲击载荷后0.12 s内,最小油膜厚度一直大于静载荷条件下的稳态值,在0.12 s之后趋于静载荷条件下的稳态值60.9 μm;当瞬态冲击载荷方向为y-方向时,最小油膜厚度在施加瞬态冲击载荷后0.028 s时达到最小值34.0 μm,在0.14 s之后趋于静载荷条件下的稳态值。

当瞬态冲击载荷为x+、x-方向时,最小油膜厚度的最小值很小,分别为15.6和18.0 μm,轴径和轴瓦发生接触的概率较大,舰船推进轴与轴瓦极有可能因擦碰而出现划伤、烧瓦等不良现象。当瞬态冲击载荷为x-方向时,最小油膜厚度恢复到静载荷条件下的稳态值的时间较长,所以轴承稳定性较差。

由图8b可见:当瞬态冲击载荷分别为x+、x-、y+、y-方向时,最大油膜压力在0.005 s时出现瞬时峰值,分别为114.29、128.61、71.02和59.22 MPa;PTFE弹塑瓦的弹性变形量在0.005 s时最大,分别为 188.8、212.0、116.9和95.1 μm;当瞬态冲击载荷为x-方向时,最大油膜压力在0.01 s出现最小值,为0.08 MPa;当瞬态冲击载荷为y+方向时,最大油膜压力在0.01 s出现最小值,为0.04 MPa。最大油膜压力在极短时间之内低于大气压力,容易造成润滑油中溶解的空气析出产生气泡,导致严重的空化,使滑动轴承润滑不良。

当瞬态冲击载荷为y-方向时,载偏角γ最小,为30.4°,最小油膜厚度的最小值较大,最小油膜厚度回到稳态值的时间较短,足以避免轴径和轴瓦的直接接触,轴承稳定性较高;最大油膜压力的最大值较小,故轴瓦的弹性变形较小,相对承载能力较大;油膜压力不会出现低于大气压力的情况,不会引起润滑剂空化而导致润滑不良。

追踪并绘制轴颈中心在4个方向瞬态冲击下的动态轴心轨迹,如图9所示:当瞬态冲击载荷方向为x+时,γ=59.6°,横向、纵向的动态轴心轨迹位移响应振幅分别为166.1和189.0 μm;当瞬态冲击载荷方向为x-时,γ=120.4°,横向、纵向的动态轴心轨迹位移响应振幅分别为373.8和203.5 μm;当瞬态冲击载荷方向为y+时,γ=149.6°,横向、纵向的动态轴心轨迹位移响应振幅分别为157.8和380.1 μm;当瞬态冲击载荷方向为y-时,γ=30.4°,横向、纵向的动态轴心轨迹位移响应振幅分别为72.7和45.7 μm。

由以上结果可知:当γ较大时,动态轴心轨迹的位移响应振幅较大,滑动轴承的工作状态不稳定;当γ较小时,动态轴心轨迹的位移响应振幅较小,滑动轴承的工作状态较稳定。因此,当舰船受到剧烈的风浪拍击时,为保证推进轴正常运转和支承滑动轴承正常工作,应当采取措施改变轴承的静载荷方向,以调整轴承偏位角,使γ减小。γ越小则滑动轴承最小油膜厚度越大,润滑状态越良好;最大油膜压力越低,PTFE弹塑瓦的变形量就越小;动态轴心轨迹的位移响应振幅越小,滑动轴承的工作状态就会越稳定。

(a)瞬态冲击载荷为x+方向 (b)瞬态冲击载荷为x-方向

(c)瞬态冲击载荷为y+方向 (d)瞬态冲击载荷为y-方向图9 瞬态冲击载荷下的动态轴心轨迹

3 结 论

本文研究了舰船在受到风浪拍击时推进轴支承滑动轴承的润滑特性和轴颈动力学响应;同时考虑瞬态冲击载荷和PTFE弹塑瓦的弹性变形,对比分析了PTFE弹塑瓦和刚性瓦滑动轴承的最小油膜厚度、最大油膜压力、轴瓦弹性变形以及动态轴心轨迹,得出以下结论。

(1)PTFE弹塑瓦的弹性变形较大,对油膜厚度分布和油膜压力分布的影响不可忽略,并且弹性变形在一定程度上可以提高滑动轴承的承载能力。

(2)当瞬态冲击载荷为x+、x-方向时,最小油膜厚度较小,舰船推进轴与轴瓦极有可能擦碰而出现划伤、烧瓦等不良现象;当瞬态冲击载荷为x-、y+方向时,最大油膜压力小于大气压力,润滑剂极有可能出现空化现象造成轴承润滑不良。

(3)瞬态冲击载荷方向与轴颈偏心方向的夹角越小,则动态轴心轨迹的位移响应振幅越小,滑动轴承的工作状态越稳定。因此,当舰船受到剧烈的风浪拍击时,应当采取措施改变轴承的静载荷方向,减小瞬态冲击载荷方向与轴承偏心方向的夹角,这样可以有效增加最小油膜厚度,降低最大油膜压力,减小动态轴心轨迹的位移响应振幅,从而改善滑动轴承的润滑状态,减小PTFE弹塑瓦的变形量,使滑动轴承的工作状态更加稳定。

[1] 马金奎, 路长厚, 陈淑江. 瞬变载荷作用下滑动轴承轴心轨迹计算仿真 [J]. 振动、测试与诊断, 2010, 30(1): 6-10.

MAR Jinkui, LU Changhou, CHEN Shujiang. Simulation of journal center trajectories of hydrodynamic journal bearing under transient loads [J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(1): 6-10.

[2] RAO T, BISWAS S, HIRANI H, et al. An analytical approach to evaluate dynamic coefficients and nonlinear transient analysis of a hydrodynamic journal bearing [J]. Tribology Transactions, 2000, 43(1): 109-115.

[3] TICHY J, BOU-SAÏD B. Hydrodynamic lubrication and bearing behavior with impulsive loads [J]. Tribology Transactions, 1991, 34(4): 505-512.

[4] 李震, 桂长林, 李志远, 等. 变载荷作用下轴-轴承系统动力学行为研究 [J]. 机械设计与研究, 2005, 21(1): 12-16.

LI Zhen, GUI Changlin, LI Zhiyuan, et al. Study on dynamic behaviors of variably-loaded shaft-bearing system [J]. Machine Design and Research, 2005, 21(1): 12-16.

[5] GADANGI R K, PALAZZOLO A B, KIM J. Transient analysis of plain and tilt pad journal bearings including fluid film temperature effects [J]. ASME Journal of Tribology, 1996, 118(2): 423-440.

[6] CHA M, KUZNETSOV E, GLAVATSKIH S. A comparative linear and nonlinear dynamic analysis of compliant cylindrical journal bearings [J]. Mechanism and Machine Theory, 2013, 64: 80-92.

[7] GLAVATSKIH S, PARAMONOV A. PTFE-faced bearing technology: advantages and practical examples [C]∥Waterpower XVI Conference Proceedings. Tulsa, Oklahoma, USA: PennWell Corporation, 2009.

[8] KUZNETSOV E, GLAVATSKIH S, FILLON M. THD analysis of compliant journal bearings considering liner deformation [J]. Tribology International, 2011, 44(12): 1629-1641.

[9] CHA M, ISAKSSON P, GLAVATSKIH S. Influence of pad compliance on nonlinear dynamic characteristics of tilting pad journal bearings [J]. Tribology International, 2013, 57: 46-53.

[10] 张国贤, 金楗, 吴白羽. EMP径向滑动轴承弹性变形的有限元求解 [J]. 润滑与密封, 2000(6): 2-4.

ZHANG Guoxian, JIN Jian, WU Baiyu. A finite element analysis of EMP journal bearing [J]. Lubrication Engineering, 2000(6): 2-4.

[11] 张直明. 滑动轴承的流体动力润滑理论 [M]. 北京: 高等教育出版社, 1986: 19-27.

[12] 罗继伟, 罗天宇. 滚动轴承分析计算与应用 [M]. 北京: 机械工业出版社, 2009: 1-2.

[13] TAYLOR R I. The inclusion of lubricant shear thinning in journal bearing models [J]. Tribology & Interface Engineering, 1999, 36: 611-619.

JournalBearingPropertiesandDynamicResponsesunderTransientImpactLoadandElasticDeformation

ZHANG Shenglun1, PEI Shiyuan1, XU Hua1,2, ZHANG Yabin3, ZHU Jie3

(1. Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China; 2. School of Mechanical Engineering, Xinjiang University, Urumqi 830046, China; 3. Hunan Sund Industrial and Technological Company Limited, Xiangtan, Hunan 411228, China)

In consideration of transient impact load and elastic deformation of bearing pad, the lubrication properties and dynamic response of journal bearing supporting the propulsion shaft of ships under the action of wind and waves are simulated. The pad of journal bearing is elastic metal-plastic pad (EMP), made of polytetrafluoroethylene (PTFE). The variations of the minimum oil film thickness and maximum oil film pressure, as well as the journal orbits in time history are investigated. Solving the Reynolds equation with finite element method, the oil-film force is converted to nodal forces of pad to calculate the elastic deformation; solving the kinetic equation of journal with Euler method, the dynamic journal orbits are obtained. Comparison of the properties between rigid bearing and EMP bearing indicates that the elastic deformation of EMP bearing cannot be neglected, and the deformation could enhance the loading capacity. Through comparative analysis on the properties and dynamic journal orbits of EMP journal bearing under the transient impact loads from four directions, it is found that adjusting the direction of the bearing static load and decreasing the angle between the directions of transient impact load and the eccentric of journal can increase the minimum oil film thickness and reduce the maximum oil film pressure, hence the displacement response amplitudes of journal orbits are decreased. Consequently, the lubricating condition, the deformation of the journal pad and the operating stability are improved.

journal bearing; transient impact load; elastic deformation; dynamic responses

2017-05-15。 作者简介: 张胜伦(1990—),男,博士生;裴世源(通信作者),男,博士,工程师。 基金项目: 国家自然科学基金资助项目(51575421);陕西省工业科技攻关资助项目(2015GY022)。

时间: 2017-10-20

网络出版地址: http:∥kns.cnki.net/kcms/detail/61.1069.T.20171020.1622.014.html

10.7652/xjtuxb201801015

TH133.31

A

0253-987X(2018)01-0100-07

(编辑 葛赵青)